区块链钱包开发系列教程
公钥密码学理论与代码实战丨区块链技术课程 #03
- Dapplink
- 发布于 2024-05-19 19:58
- 阅读 4815
密码学中的加密方式从密钥的数量方向可以分为 对称加密和非对称加密 , 对称加密 只使用一把密钥来对数据进行加解密,而 非对称加密 使用两把密钥来进行加密,分别为公钥和私钥。对称加密和非对称加密有很多非常出名的算法,例如:对称加密比较有名的算法有 DES 和 AES
作者丨Seek

密码学中的加密方式从密钥的数量方向可以分为 对称加密和非对称加密 , 对称加密 只使用一把密钥来对数据进行加解密,而 非对称加密 使用两把密钥来进行加密,分别为公钥和私钥。对称加密和非对称加密有很多非常出名的算法,例如:对称加密比较有名的算法有 DES 和 AES ,非对称加密有 RSA 和 ECC 。
对称加密和非对称加密各有优缺点,那么 咱们怎么去利用他们的优缺点呢?
本章我们将分别 从理论和实践的角度分析对称加密和非对称加密,让更加容易地理解对称加密和非对称加密。
我们都知道, 密码体制有两种: 对称密码体制( 又称为单钥密码体制) 和非对称密码体制( 又称为双钥密码体制或公钥密码体制) 。 对称密码体制 使用相同的密钥( 秘密密钥) 对消息进行加密/解密,系统的保密性主要由密钥的安全性决定,而与算法是否保密无关。
对称密码体制设计和实现的中心是: 用何种方法产生满足保密要求的密钥以及用何种方法将密钥安全又可靠地分配给通信双方。 对称密码体制可以通过分组密码或流密码来实现,它既可以用于数据加密,又可以用于消息认证。非对称密码体制使用公钥加密消息,使用私钥来解密。使用 非对称密码体制可增强通信的安全性 。
在密码学体系中, 对称加密、非对称加密、单向散列函数、消息认证码、数字签名和伪随机数生成器被统称为密码学家的工具箱 。其中,对称加密和非对称加密主要是用来保证机密性;单向散列函数用来保证消息的完整性;消息认证码的功能主要是认证;数字签名保证消息的不可抵赖性。这篇文章所要讲诉的就是保证消息的机密性的对称密码和非对称密码。
公钥密码学理论与代码实战
对称加密 又称单密钥加密,整个加密过程中只使用一个密钥。 所谓对称其实就是使用一把密钥加密,使用同一把密钥解密。对称加密由于加解和解密使用的是同一个密钥算法,故而在加解密的过程中速度比较快,适合于数据量比较大的加解密。
对称加密的 主要有优点就是算法公开、计算量小、加密速度快、加密效率高 ;但是它也存在强大的缺点, 缺点就是密钥协商过程中,一旦密钥泄露,别人可以获取到密钥,这样也能对密文进行解密 。另外,每对用户每次使用对称加密算法时,都需要使用其他人不知道的独一密钥, 这会使得收、发双方所拥有的钥匙数量巨大,密钥管理成为双方的负担 。
常用的对称加密算法有 DES、3DES、AES、TDEA、Blowfish、RC2、RC4 和 RC5 等。
本文我们讲讲解两种经典的对称加密算法。
1.1 DES
1.1.1 算法介绍
DES 加密解密算法最初由美国 IBM 公司研究人员所设计发明,且为第一个公开的商用密码算法标准,自诞生以来便得到了 ISO 的一致认可。DES 是分组密码算法的典型代表,它的明文分组长度为 64bits,密钥长度为 64bits,其中包括有 8bits 的奇偶校验,因此有效密钥长度为 56bits。DES 加密解密算法使用的过程相同,且可以随时均都可以进行变动。它们其中有极少数被认为是易破解的弱密钥,但是很容易抛开它们不使用,因此其自身安全性主要依赖于有效密钥。
DES 算法加密过程首先先对明文分组进行操作,需要加密的明文分为每块 64bits 的固定大小。 下图所示左右两部分分别为64bits 的明文分组加密过程和其 16 个子密钥生成的过程。
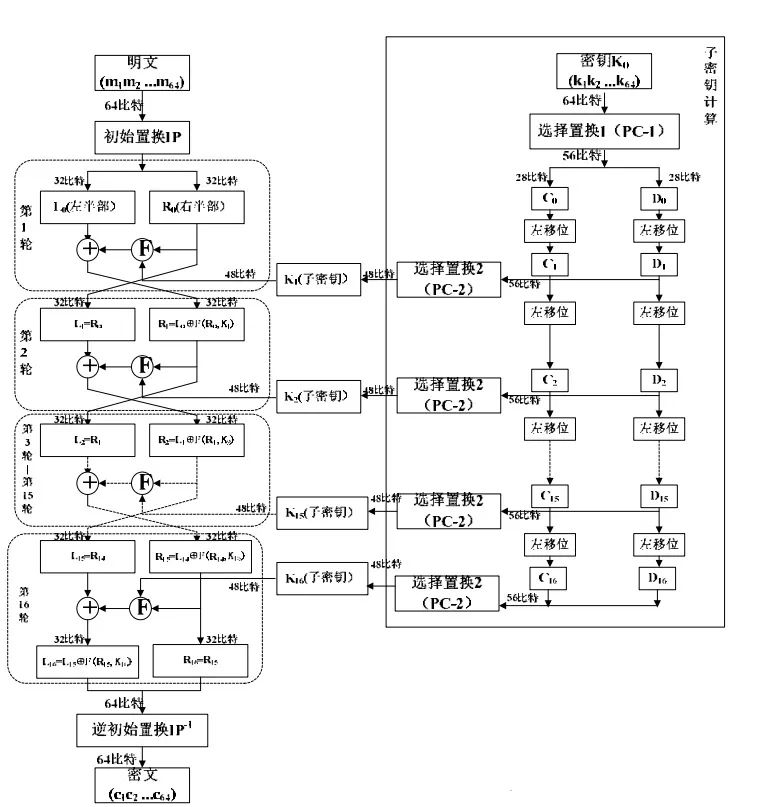
1.1.2 算法细节流程描述
DES 采用 Feistel 结构,具体流程如下:
初始置换(Initial Permutation,IP)
加密过程开始时,首先对 64 比特的明文进行初始置换。这只是一个重新排列比特位置的过程,没有实际的加密效果。
轮函数(Feistel Function,F)
DES 包含 16 轮相同的操作,每轮操作都使用一个不同的子密钥。每轮操作包括以下步骤:

子密钥生成: 每轮使用的 48 比特子密钥由 56 比特的主密钥通过置换选择和压缩生成。
逆初始置换(Inverse Initial Permutation,IP^{-1} :16 轮加密操作完成后,将最终的左右部分组合成一个 64 比特的中间结果,经过逆初始置换得到密文。
解密过程: 解密过程与加密过程基本相同,区别在于子密钥的使用顺序相反。即解密时使用子密钥的顺序为 𝐾16,𝐾15,…,𝐾1K16,K15,…,K1。
1.1.3 算法安全性问题
尽管 DES 设计时考虑了多种攻击方式,但由于密钥长度较短(56 比特),它容易受到暴力破解(brute-force attack)。目前,DES 已被认为不再安全,通常使用其增强版 3DES 或更先进的 AES。
1.1.4 go 代码加解密实战
package main
import (
"crypto/cipher"
"crypto/des"
"encoding/hex"
"fmt"
"log"
"bytes"
)
func main() {
key := []byte("s3cr3t_k")
plaintext := []byte("Go DES Encryption")
// 加密
ciphertext, err := encrypt(key, plaintext)
if err != nil {
log.Fatalf("encryption error: %v", err)
}
fmt.Printf("Ciphertext (hex): %s\n", hex.EncodeToString(ciphertext))
// 解密
decryptedText, err := decrypt(key, ciphertext)
if err != nil {
log.Fatalf("decryption error: %v", err)
}
fmt.Printf("Decrypted text: %s\n", string(decryptedText))
}
func encrypt(key, plaintext []byte) ([]byte, error) {
block, err := des.NewCipher(key)
if err != nil {
return nil, err
}
// 填充数据
plaintext = pkcs5Padding(plaintext, block.BlockSize())
ciphertext := make([]byte, len(plaintext))
mode := cipher.NewCBCEncrypter(block, key)
mode.CryptBlocks(ciphertext, plaintext)
return ciphertext, nil
}
func decrypt(key, ciphertext []byte) ([]byte, error) {
block, err := des.NewCipher(key)
if err != nil {
return nil, err
}
decrypted := make([]byte, len(ciphertext))
mode := cipher.NewCBCDecrypter(block, key)
mode.CryptBlocks(decrypted, ciphertext)
// 去除填充
decrypted = pkcs5Unpadding(decrypted)
return decrypted, nil
}
func pkcs5Padding(data []byte, blockSize int) []byte {
padding := blockSize - len(data)%blockSize
padtext := bytes.Repeat([]byte{byte(padding)}, padding)
return append(data, padtext...)
}
func pkcs5Unpadding(data []byte) []byte {
length := len(data)
unpadding := int(data[length-1])
return data[:(length - unpadding)]
}1.2 3DES
三重数据加密标准 (Triple Data Encryption Standard,简称 3DES)是一种对称加密算法,用于提高 DES 的安全性。3DES 通过对数据执行三次 DES 加密操作,有效地增加了密钥长度和安全性。
3DES 的工作方式是在三个 DES 加密过程之间交替执行加密和解密。 具体流程如下:
1.2.1 加密过程

1.2.2 解密过程

1.2.3 密钥选项
3-Key 3DES: 使用三个独立的密钥 𝐾1、𝐾2、𝐾3,密钥长度为 168 比特。
2-Key 3DES: 使用两个密钥 𝐾1K、𝐾2,其中 𝐾1=𝐾3,密钥长度为 112 比特。
1-Key 3DES: 使用一个密钥 𝐾,其中 𝐾1=𝐾2=𝐾3,等同于单次 DES,不推荐使用。
1.2.4 安全性
3DES 提供的安全性比单一 DES 高得多。即便使用暴力破解法,破解 3DES 所需的时间远超破解 DES 所需的时间。但由于 3DES 的计算复杂性较高,效率相对较低,现在通常推荐使用 AES(高级加密标准)代替 3DES。
1.2.5 代码示范
package main
import (
"crypto/cipher"
"crypto/des"
"encoding/hex"
"fmt"
"log"
"bytes"
)
func main() {
key := []byte("s3cr3t_k1s3cr3t_k2s3cr3t_k3")
plaintext := []byte("Go 3DES Encryption")
// 加密
ciphertext, err := encrypt(key, plaintext)
if err != nil {
log.Fatalf("encryption error: %v", err)
}
fmt.Printf("Ciphertext (hex): %s\n", hex.EncodeToString(ciphertext))
// 解密
decryptedText, err := decrypt(key, ciphertext)
if err != nil {
log.Fatalf("decryption error: %v", err)
}
fmt.Printf("Decrypted text: %s\n", string(decryptedText))
}
func encrypt(key, plaintext []byte) ([]byte, error) {
block, err := des.NewTripleDESCipher(key)
if err != nil {
return nil, err
}
// 填充数据
plaintext = pkcs5Padding(plaintext, block.BlockSize())
ciphertext := make([]byte, len(plaintext))
mode := cipher.NewCBCEncrypter(block, key[:8])
mode.CryptBlocks(ciphertext, plaintext)
return ciphertext, nil
}
func decrypt(key, ciphertext []byte) ([]byte, error) {
block, err := des.NewTripleDESCipher(key)
if err != nil {
return nil, err
}
decrypted := make([]byte, len(ciphertext))
mode := cipher.NewCBCDecrypter(block, key[:8])
mode.CryptBlocks(decrypted, ciphertext)
// 去除填充
decrypted = pkcs5Unpadding(decrypted)
return decrypted, nil
}
func pkcs5Padding(data []byte, blockSize int) []byte {
padding := blockSize - len(data)%blockSize
padtext := bytes.Repeat([]byte{byte(padding)}, padding)
return append(data, padtext...)
}
func pkcs5Unpadding(data []byte) []byte {
length := len(data)
unpadding := int(data[length-1])
return data[:(length - unpadding)]
}1.3 AES
AES 加密算法为分组密码,分组长度为 128 位即 16 个字节,密匙长度有128、192 或 256 位,根据密匙 长 度的不同,加密的轮数也不同,本文采用长度为 128 位的密匙,加密轮数为 10 轮。AES 加密算法不仅编码紧凑、设计简单而且可抵抗多种类型的攻击,其基本结构包括 4个部分。这四个部分分别为字节替换、行位移、列混合和轮密匙加。
AES 基于代换-置换网络(Substitution-Permutation Network,SPN),其加密过程包括多个轮次(Rounds),具体轮次数取决于密钥长度:
-
AES-128:10 轮
-
AES-192:12 轮
-
AES-256:14 轮
每轮包含以下操作:
1.3.1 初始轮
轮密钥加(AddRoundKey):将输入的明文数据块与轮密钥进行异或(XOR)操作。
1.3.2 主要轮
每轮包括以下四个步骤:
字节代换(SubBytes): 使用 S 盒(Substitution box)逐字节替换数据块中的每个字节。
行移位(ShiftRows): 对数据块中的每一行进行循环左移操作。
列混淆(MixColumns): 对数据块中的每一列进行线性变换操作。
轮密钥加(AddRoundKey): 将数据块与当前轮密钥进行异或操作。
1.3.3 最终轮
最终轮与主要轮类似,但省略了列混淆(MixColumns)步骤。
1.3.4 详细步骤
假设我们使用 AES-128,具体步骤如下:
1.3.4.1 主要轮

1.3.4.2 最终轮
-
字节代换(SubBytes)
-
行移位(ShiftRows)
-
轮密钥加(AddRoundKey)
1.3.5 密钥扩展
AES 的密钥扩展算法用于生成每轮的轮密钥(Round Keys),从主密钥生成多个轮密钥。具体步骤包括:
-
主密钥初始化: 将主密钥分成若干个 32 比特的字(Words)。
-
扩展过程: 每个新字由前一个字和若干前置字经过非线性变换(SubWord 和 RotWord)以及轮常量(Rcon)异或得到。
1.3.6 示范代码
package main
import ( "crypto/aes" "crypto/cipher" "encoding/hex" "fmt" "log" "bytes" )
func main() { key := []byte("examplekey123456") // 16 bytes for AES-128 plaintext := []byte("Go AES Encryption")
// 加密 ciphertext, err := encrypt(key, plaintext) if err != nil { log.Fatalf("encryption error: %v", err) } fmt.Printf("Ciphertext (hex): %s\n", hex.EncodeToString(ciphertext))
// 解密 decryptedText, err := decrypt(key, ciphertext) if err != nil { log.Fatalf("decryption error: %v", err) } fmt.Printf("Decrypted text: %s\n", string(decryptedText)) }
func encrypt(key, plaintext []byte) ([]byte, error) { block, err := aes.NewCipher(key) if err != nil { return nil, err }
// 填充数据 plaintext = pkcs7Padding(plaintext, aes.BlockSize) ciphertext := make([]byte, aes.BlockSize+len(plaintext))
iv := ciphertext[:aes.BlockSize] mode := cipher.NewCBCEncrypter(block, iv) mode.CryptBlocks(ciphertext[aes.BlockSize:], plaintext)
return ciphertext, nil }
func decrypt(key, ciphertext []byte) ([]byte, error) { block, err := aes.NewCipher(key) if err != nil { return nil, err }
if len(ciphertext) < aes.BlockSize { return nil, fmt.Errorf("ciphertext too short") }
iv := ciphertext[:aes.BlockSize] ciphertext = ciphertext[aes.BlockSize:]
mode := cipher.NewCBCDecrypter(block, iv) mode.CryptBlocks(ciphertext, ciphertext)
// 去除填充 plaintext := pkcs7Unpadding(ciphertext) return plaintext, nil }
func pkcs7Padding(data []byte, blockSize int) []byte { padding := blockSize - len(data)%blockSize padtext := bytes.Repeat([]byte{byte(padding)}, padding) return append(data, padtext...) }
func pkcs7Unpadding(data []byte) []byte { length := len(data) unpadding := int(data[length-1]) return data[:(length - unpadding)] }
## 非对称加密
**非对称加密又称为公钥密码,该技术是针对私钥密码体制(对称加密算法)的缺陷被提出来的,** 非对称加密会产生两把密钥,分别为 **公钥(Public Key)和私钥(Private Key),** 其中一把密钥用于加密,另一把密钥用于解密。非对称加密的特征是算法强度复杂、安全性依赖于算法与密钥但是由于其算法复杂,而使得加密解密速度没有对称加密解密的速度快。对称密码体制中只有一种密钥,并且是非公开的,如果要解密就得让对方知道密钥。所以保证其安全性就是保证密钥的安全, **而非对称密钥体制有两种密钥,其中一个是公开的,这样就可以不需要像对称密码那样传输对方的密钥了。这样安全性就高了很多。**
常用的非对称加密算法有 **RSA、Elgamal、背包算法、Rabin、D-H、ECC(椭圆曲线加密算法)** 等。
### **2.1 RSA**
**RSA 算法是一种迄今为止理论上比较成熟和完善的公钥密码体制,是非对称密码体制的典型代表。** 在网络、信息安全等许多方面都使用 RSA 算法,特别是 RSA 算法典型应用在通信中的数字签名,可实现对手的身份、不可抵赖性验证。 **在身份认证、信息安全、电子商务中有着广泛的应用前景** 。
#### **2.1.1 密钥生成**
- 选择两个大素数: 选择两个大素数 𝑝p 和 𝑞q。
**计算模数 𝑛**
- 𝑛=𝑝×𝑞
**计算欧拉函数 𝜙(𝑛)**
- 𝜙(𝑛)=(𝑝−1)×(𝑞−1)
**选择公钥指数 𝑒**
- 选择一个整数 𝑒 满足 1<𝑒<𝜙(𝑛) 且 𝑒与 𝜙(𝑛) 互质。
**计算私钥指数 𝑑**
- 计算 𝑑使得 𝑑×𝑒≡1 mod 𝜙(𝑛),即 𝑑 是 𝑒 在模 𝜙(𝑛) 下的乘法逆元。
#### **2.1.2 公钥和私钥**
- 公钥:(𝑒,𝑛)
- 私钥:(𝑑,𝑛)
#### **2.1.3 加密过程**
假设明文为 𝑀,加密得到密文 𝐶 的过程如下:
#### **2.1.4 解密过程**
假设密文为 𝐶,解密得到明文 𝑀 的过程如下:
#### **2.1.5 签名和验证**
数字签名: 用私钥对消息 𝑀M 进行签名,得到签名 𝑆:
验证签名: 用公钥验证签名 𝑆,验证得到消息 𝑀′:
如果 𝑀′=𝑀,则签名验证通过。
#### **2.1.6 总结**
RSA 是一种基于大数分解难题的非对称加密算法,广泛应用于数据加密和数字签名。其基本流程包括密钥生成、加密、解密、签名和验证。理解 RSA 算法的原理和实现方法对于应用现代密码学技术具有重要意义。
#### **2.1.7 代码实战** package main
import ( "crypto/rand" "crypto/rsa" "crypto/sha256" "crypto/x509" "encoding/pem" "fmt" "log" )
// 生成 RSA 密钥对 func generateKeys(bits int) (*rsa.PrivateKey, error) { privKey, err := rsa.GenerateKey(rand.Reader, bits) if err != nil { return nil, err } return privKey, nil }
// 加密 func encrypt(publicKey *rsa.PublicKey, message []byte) ([]byte, error) { ciphertext, err := rsa.EncryptOAEP(sha256.New(), rand.Reader, publicKey, message, nil) if err != nil { return nil, err } return ciphertext, nil }
// 解密 func decrypt(privateKey *rsa.PrivateKey, ciphertext []byte) ([]byte, error) { plaintext, err := rsa.DecryptOAEP(sha256.New(), rand.Reader, privateKey, ciphertext, nil) if err != nil { return nil, err } return plaintext, nil }
// 密钥转为 PEM 格式字符串 func exportPrivateKeyAsPEM(privKey *rsa.PrivateKey) string { privKeyBytes := x509.MarshalPKCS1PrivateKey(privKey) privKeyPEM := pem.EncodeToMemory(&pem.Block{ Type: "RSA PRIVATE KEY", Bytes: privKeyBytes, }) return string(privKeyPEM) }
func exportPublicKeyAsPEM(pubKey *rsa.PublicKey) string { pubKeyBytes, err := x509.MarshalPKIXPublicKey(pubKey) if err != nil { log.Fatalf("Error converting public key to bytes: %v", err) } pubKeyPEM := pem.EncodeToMemory(&pem.Block{ Type: "RSA PUBLIC KEY", Bytes: pubKeyBytes, }) return string(pubKeyPEM) }
func main() { // 生成 RSA 密钥对 bits := 2048 privKey, err := generateKeys(bits) if err != nil { log.Fatalf("Error generating keys: %v", err) } pubKey := &privKey.PublicKey
// 输出密钥 fmt.Println("Private Key:") fmt.Println(exportPrivateKeyAsPEM(privKey)) fmt.Println("Public Key:") fmt.Println(exportPublicKeyAsPEM(pubKey))
// 加密 message := []byte("Hello, RSA!") ciphertext, err := encrypt(pubKey, message) if err != nil { log.Fatalf("Error encrypting message: %v", err) } fmt.Printf("Ciphertext: %x\n", ciphertext)
// 解密 decryptedMessage, err := decrypt(privKey, ciphertext) if err != nil { log.Fatalf("Error decrypting message: %v", err) } fmt.Printf("Decrypted Message: %s\n", decryptedMessage) }
### **1.2 ECC**
椭圆曲线加密算法(ECC)是基于椭圆曲线数学的一种非对称密码算法,是建立在基于椭圆曲线的离散对数问题上的密码体制。随着分解大整数方法的进步以及各方面的完善,RSA 算法渐渐不能满足现状,ECC 算法的需求性逐渐增大。ECC 以其明显的“短密钥”优势得到了广泛应用,并逐渐被确定为许多编码方式的数字签名标准。当然,ECC 还有许多未解决的问题,不过这种引用了丰富数学理论的算法,也印证了将更多数学有较大可行性理论应用到密码学这一领域中。
首先从数学角度阐释算法加密原理,ECC椭圆曲线加密算法数学基础是利用有限域上椭圆曲线离散对数问题(ECDLP)的计算困难性,所谓椭圆曲线是指由韦尔斯特拉方程。其椭圆曲线方程如下:
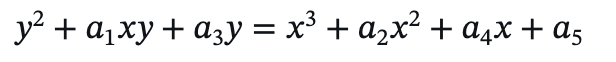
其中 a1 a2 a3 a4 a5 属于 K。当域 K 的特征为不同值时,上述方程也能进行相应的化 简得到不同的椭圆曲线表达式:
当域 K 的特征 char(K)≠2 或 3,椭圆曲线方程的表达式可化简为:
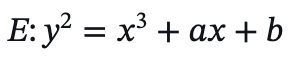
当域 K 的特征 char(K)=2,椭圆曲线方程的表达式可化简为:
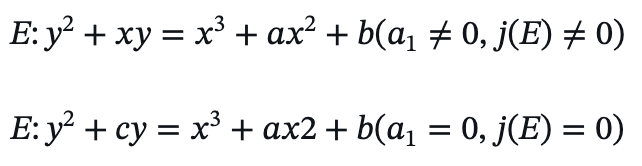
而当域 K 的特征 char(K)=3,椭圆曲线方程有如下表达式:
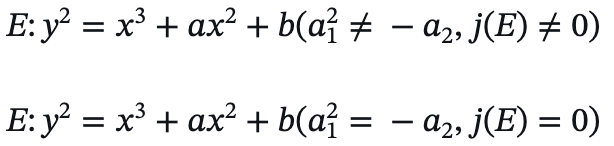
在实际应用的时候,还需要确定曲线上点群的阶。通过运用如下相关经典的定理便能得出点群的阶
定理 2.1(Hasse 定理) 若 E 是定义在域 Fq上的一条椭圆曲线,用 M 来表示 E 上 Fq-点的个数,那么有:
|M=(q+1)| <= 2倍根号q
定理 2.2 有椭圆曲线 E 是定义在域 Fq上的,a1是 q 上的相关映射,
当 n≥1 时有 E(Fq^n) = q^n +1 -an。
于是有 an= a1an-1 -qan-2
#### **2.2.1 ECC 算法详解**
**参数设定**
- 椭圆曲线定义:选择一个合适的椭圆曲线 𝐸。
- 基点 𝐺 的选择:选择椭圆曲线上的一个基点 𝐺。
- 素数阶 𝑛n 的选择:确定基点 𝐺 的阶 𝑛,即 𝑛×𝐺=𝑂,其中 𝑂 是无穷远点。
- 公钥和私钥长度:确定密钥的长度,通常使用椭圆曲线上的点 𝑄 表示公钥,私钥为一个随机数 𝑑。
**密钥生成**
- 选择私钥 𝑑:选择一个随机数 𝑑d,满足 1≤𝑑<𝑛。
- 计算公钥 𝑄:通过标量乘法计算 𝑄=𝑑×𝐺。
**加密过程**
- 选择随机数 𝑘:选择一个随机数 𝑘,满足 1≤𝑘<𝑛。
- 计算椭圆曲线点 𝑃:通过标量乘法计算 𝑃=𝑘×𝐺。
- 计算共享密钥 𝐾:使用椭圆曲线点 𝑃 和公钥 𝑄 计算共享密钥 𝐾 ,通常使用 𝑥 坐标作为共享密钥。
- 加密消息:使用共享密钥 𝐾 对消息进行对称加密,例如使用 AES 等算法。
**解密过程**
- 计算椭圆曲线点 𝑃:接收到的密文中包含椭圆曲线点 𝑃。
- 计算共享密钥 𝐾:使用私钥 𝑑 和椭圆曲线点 𝑃 计算共享密钥 𝐾。
- 解密消息:使用共享密钥 𝐾 对密文进行对称解密,得到原始消息。
**签名和验证**
- ECC 也可以用于数字签名。签名过程类似于加密过程,但使用私钥对消息的摘要进行签名。验证过程使用公钥验证签名的有效性。
#### **2.2.2 安全性**
ECC 的安全性基于椭圆曲线离散对数问题(ECDLP),即给定 𝑃 和 𝑄=𝑑×𝑃,求解 𝑑 的难度。目前没有已知有效的经典或量子算法能够有效解决 ECDLP 问题。
#### **2.2.3 示范代码** package main
import ( "crypto/ecdsa" "crypto/elliptic" "crypto/rand" "fmt" )
func main() { // 生成椭圆曲线密钥对 privKey, err := ecdsa.GenerateKey(elliptic.P256(), rand.Reader) if err != nil { fmt.Println("Error generating key:", err) return }
// 加密过程 message := []byte("Hello, ECC!") ciphertext, err := encrypt(privKey.PublicKey, message) if err != nil { fmt.Println("Error encrypting message:", err) return }
// 解密过程 decryptedMessage, err := decrypt(privKey, ciphertext) if err != nil { fmt.Println("Error decrypting message:", err) return }
fmt.Println("Original message:", string(message)) fmt.Println("Decrypted message:", string(decryptedMessage)) }
// 加密 func encrypt(pubKey ecdsa.PublicKey, message []byte) ([]byte, error) { // 生成临时密钥对 tmpPrivKey, err := ecdsa.GenerateKey(elliptic.P256(), rand.Reader) if err != nil { return nil, err }
// 计算共享密钥 x, _ := pubKey.Curve.ScalarMult(pubKey.X, pubKey.Y, tmpPrivKey.D.Bytes())
// 对消息进行对称加密,这里简化为拼接 ciphertext := append(x.Bytes(), message...)
return ciphertext, nil }
// 解密 func decrypt(privKey *ecdsa.PrivateKey, ciphertext []byte) ([]byte, error) { // 解析共享密钥 x := new(big.Int).SetBytes(ciphertext[:32]) y := new(big.Int).SetBytes(ciphertext[32:]) sharedKeyX, _ := privKey.PublicKey.Curve.ScalarMult(x, y, privKey.D.Bytes())
// 解密消息 decryptedMessage := ciphertext[64:] // 假设前 64 个字节为共享密钥 return decryptedMessage, nil }
### **2.3 ECC 算法之 ECDSA 和 EDDSA**
ECDSA(Elliptic Curve Digital Signature Algorithm)和 EdDSA(Edwards-curve Digital Signature Algorithm)都是基于椭圆曲线的数字签名算法,但它们使用了不同的曲线模型和数学原理。
#### **2.3.1 ECDSA(Elliptic Curve Digital Signature Algorithm)**
- **曲线模型** :ECDSA 使用的是 Weierstrass 曲线。
- **安全性:** ECDSA 的安全性基于椭圆曲线离散对数问题(ECDLP),即给定 𝑃 和 𝑄=𝑑×𝑃,求解 𝑑 的难度。
- **应用:** ECDSA 在 TLS/SSL、SSH、数字签名等领域广泛应用。
#### **2.3.2 EdDSA(Edwards-curve Digital Signature Algorithm)**
- **曲线模型:** EdDSA 使用的是 Edwards 曲线。
- **安全性:** EdDSA 的安全性基于哈希到点(Hash-to-Point)和点到点哈希(Point-to-Point Hashing),这种方式抵抗了侧信道攻击和冯·诺依曼攻击,并且提供了更好的安全性。
- **应用:** EdDSA 由 Daniel J. Bernstein 等人提出,并且被应用于密码学协议中,如密码学货币、加密货币等。
#### **2.3.3 EdDSA 和 ECDSA 比较**
- ECDSA 和 EdDSA 都是基于椭圆曲线的数字签名算法,但它们使用了不同的曲线模型和数学原理。
- ECDSA 是使用 Weierstrass 曲线的数字签名算法,而 EdDSA 是使用 Edwards 曲线的数字签名算法。
- 在安全性方面,EdDSA 提供了更好的安全性,并且抵抗了一些 ECDSA 存在的攻击。
- 在实践中,选择 ECDSA 还是 EdDSA 取决于具体的应用场景和性能需求。
### **2.4 ECDSA 特别算法 Secp256K1**
Secp256k1 是一种椭圆曲线,常用于加密货币领域,如比特币和以太坊。以下是
**Secp256k1 算法的基本流程:**
#### **2.4.1 参数设定**
- **椭圆曲线方程:** Secp256k1 使用的椭圆曲线方程为
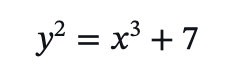
- **有限域参数:** Secp256k1 曲线定义在素数域上,具体的参数如下:素数 𝑝:
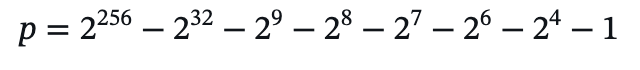
曲线参数 𝑎:𝑎=0
曲线参数 𝑏:𝑏=7
- **基点 𝐺 的选择:** Secp256k1 曲线上的基点 𝐺G 是一个预定义的点,其横坐标和纵坐标的值已经确定。
#### **2.4.2 密钥生成**
- 选择私钥 𝑑:选择一个随机数 𝑑,满足 1≤𝑑<𝑛,其中 𝑛 是曲线的阶。
- 计算公钥 𝑄:通过标量乘法计算 𝑄=𝑑×𝐺。
#### **2.4.3 签名过程**
- 选择随机数 𝑘:选择一个随机数 𝑘,满足 1≤𝑘<𝑛。
- 计算椭圆曲线点 𝑅:通过标量乘法计算 𝑅=𝑘×𝐺。
- 计算 𝑟:𝑟 是 𝑅 的横坐标的模 𝑛 的值。
- 计算 𝑠:计算消息的哈希值 𝐻。
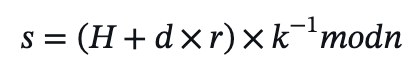
- 签名:签名 (𝑟,𝑠)即为最终签名结果。
#### **2.4.4 验证过程**
- 验证 𝑟:验证 𝑟r 是否满足 1≤𝑟<𝑛。
- 计算 𝑢1:
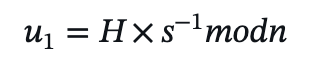
- 计算 𝑢2:
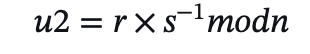
- 计算椭圆曲线点 𝑅':
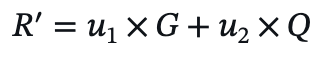
- 验证 𝑅′:验证 𝑅′ 的横坐标的模 𝑛 是否等于 𝑟。若相等,则验证通过。
### **2.5 EdDSA 特别算法 Ed25519**
Ed25519 是一种基于 Edwards 曲线的数字签名算法,它提供了高度的安全性和性能;Ed25519 也是加密货币中使用比较广泛的签名算法,如波卡等链。
**以下是 Ed25519 算法的基本流程:**
#### **2.5.1 参数设定**
- 曲线模型:Ed25519 使用的是 Edwards 曲线模型。
- 椭圆曲线参数:Ed25519 使用的是 Ed25519 曲线,其参数已经预先定义。
#### **2.5.2 密钥生成**
- 选择私钥 𝑠𝑘:选择一个随机的 256 位(32 字节)的私钥。
- 计算公钥 𝑝𝑘:通过基于私钥生成公钥的算法,计算出对应的公钥。
#### **2.5.3 签名过程**
- 计算消息的哈希值:使用哈希函数(如 SHA-512)计算消息的哈希值。
- 生成随机数:生成一个 512 位(64 字节)的随机数。
- 计算扩展密钥:使用随机数、私钥和消息哈希值生成扩展密钥。
- 生成签名:使用扩展密钥和消息哈希值生成签名。
#### **2.5.4 验证过程**
- 计算消息的哈希值:使用相同的哈希函数计算消息的哈希值。
- 验证签名:使用公钥、消息的哈希值和签名来验证消息的完整性和真实性。
## 混合加密-对称加密和非对称加密的实际应用场景
**所谓混合加密就是使用在实际的应用中把对称加密和非对称加密结合起来使用。**
我们都知道非对称加密算法比对称加密算法慢数千倍,但 **在保护通信安全方面,非对称加密算法却具有对称密码难以企及的优势。** 所以在实际的应用中,都是 **对称加密与非对称加密混合使用。** 取其优势,去其糟粕,达到完美使用的一个目的。
**对称加密技术,** 即专用密钥加密技术或单钥密码技术,加密密钥与解密密钥一致,发送方与接收方用同一组的公私密钥对加密或者解密信息。数据加密的一个关键要求是有相同的密钥才能解密。因为通信双方共享密钥,如果密钥丢失或泄露,那么获取密钥的人就可以加密或者解密数据,所以为保证消息的机密性必须保障密钥的安全。这种算法比较简单且计算量比较小,对网络开放、从而能够效率高地加密。同时存在的缺点,一是通讯双方基于通过非面对面的方式协商一个共同的密钥,因此不能保证协商过程的安全性。二是通讯双方每次进行数据传输时都使用惟一密钥,这使得对称加密技术在开放型的网络中需要使用和生成大量的密钥,对于密钥的管理就成为用户的很大负担。三是对称加密算法只能对数据进行加解密,保证数据的机密性,但无法验证通讯双方的真实身份,不能确定数据的完整性。
**非对称密钥加密技术,** 由公钥和私钥形成一个密钥对,其中公钥向公众公开,私钥归密钥持有人单独保管。通讯双方使用非对称密钥对数据进行加密和解密时,必须使用相互匹配的公钥和私钥。它有两种方式:一种是发送方用接收方的公钥来加密信息,接收方用其私钥解密信息,这样接收方可以收到多个发送方传来的加密数据,且此加密数据只有接收方一个用户可以解读;另一种即发送方利用自身的私钥加密信息,接收方用对方公钥解密信息,这样一个信息有可能被多个接收方解密。非对称密钥加密技术的优点是简化了密钥的发放及管理的过程,支持数字签名等安全认证技术,缺点是加密和解密的计算过程特别复杂,运行数据加密和解密的速度比较慢。