流言终结者:助记词碰撞骗局背后的奥妙
- Keystone
- 发布于 2024-07-10 21:55
- 阅读 14600
助记词碰撞有多高的难度?
1.助记词碰撞:一个不靠谱的骗局
刚刚接触加密货币的小伙伴们,往往会好奇这样一个问题: 现如今 GPU 算力这么强,有没有可能通过遍历助记词组合,碰撞出有资产的钱包? 其实这也是币圈的一个古典骗局:助记词碰撞器。这种想法为何不靠谱?我们来做一些数学计算看看:
已知 BIP39 标准的助记词库一共有 2048 个单词,计算一下可以产生多少种 12 个单词的助记词组合:
$$ P(2048,12) = 2048!/(2048-12)! ≈ 5.27× 10^{39} $$
一张 RTX4090 的显卡的哈希率大约为 125MH/秒(1.25 亿次),如果用它来遍历完所有的助记词组合需要花费 $$1.38×10^{24} $$年,很显然在我们有限的生命里是等不到了。 有些人可能会想,我不需要遍历所有的助记词,只要命中一个也是赚的。根据 @ycharts 的数据显示,目前以太坊的总地址数为 2.73 亿个,这个数量仅仅是助记词组合最大值的 $$ 1/ 5×10^{32} $$。换句话说,你碰撞出一个已有地址的时间也需要 1.27×10^17 年,同样是远超人类文明尺度存在的时长。 既然助记词被碰撞的概率如此低,是否代表我们生成的助记词组就是高枕无忧的呢?实际上,在满足某些特定前提下,别人是可以通过撞库获取得到你的完整助记词组。 第一种情况,12 个单词的助记词组中有 8 个单词泄露了,使用 1 张 RTX4090 的算力便可以在 30 天内算出剩余的 4 个单词,所以只泄露部分助记词也是存在风险的。
还有一种情况是,钱包使用的随机数生成器存在漏洞,导致助记词的实际生成范围被大大缩小,那么破解助记词组的难度也会因此大幅降低。这里我们来科普一下加密货币最核心的一个要素——随机数的安全性。
2. 从随机数到助记词
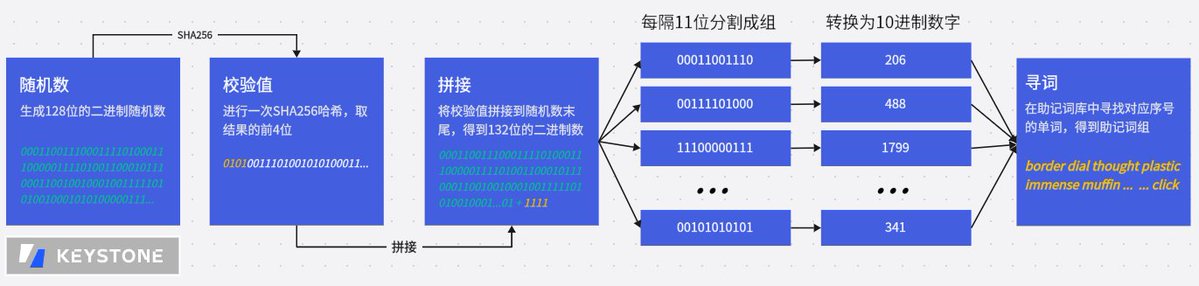
我们先了解一套 12 位助记词是如何产生的:
-
计算机先随机产生一个二进制的 128 位数字 A。
-
对 A 进行一次哈希计算,并且将哈希结果的前4位加到 A 的末尾,得到一个 132 位的二进制数 B。
-
按照 11 位数字为 1 组的规则,将 B 分成 12 组二进制数字。
-
每组二进制数字转为十进制数字,在助记词库中找到对应序号的单词。
-
最终 12 个单词就形成了一套助记词组合。
不难看出生成钱包的关键就在于第一步所产生的随机数,后面的流程都是将它按照一定规则转换成助记词,来帮助我们记录。随机数决定了钱包的一切,因此这个随机数产生的质量高低,也影响着我们的资产安全性。
3. 随机数生成器的奥妙
可能许多人并不了解,随机数产生器主要包括伪随机(PRNG)和真随机(TRNG)两种,正如他们的字面意思一样: 伪随机数是基于确定性的算法产生的数字,它生成速度比较快,只需要输入一个种子值,再依据特定的算法,就可以获得结果,只要种子的值相同就会生成相同的随机数结果序列。 而真随最终 12 个单词就形成了一套助记词组合。些无法预测的物理现象来产生随机数,比如天气状况、手机陀螺仪的加速度值甚至是放射性物质随机发射出的β粒子等等。一般来说 TRNG 会采用多个不同来源的物理数据来共同生成随机数,避免单点失效的风险。 有人曾经做过一个测试,比较了某款 TRNG(真随机数发生器)和某款 PRNG(伪随机数发生器)生成的随机图像。测试流程是产生随机的坐标,并在画布上对应的坐标处画上黑色点。经过多轮操作后,得到最终的图像。结果显示,TRNG 生成的图片上黑点杂乱无章,而 PRNG 生成的图片中,在杂乱的图像里仍能辨认出某种规律性。
伪随机数由于其适用性广,生成速度快等优势在许多场合使用,但在涉及安全的场合,使用伪随机数生成器,可能会带来严重的后果。如 TrustWallet 在 2023 年发布公告,其在某些版本的浏览器扩展钱包中,使用了伪随机数生成器 MT19937,但由于其无法提供足够随机性,有生成相同助记词的潜在风险,因此他们披露了这个问题并引导受影响的用户转移资产并更新到新版本。
4.随机数生成器在钱包中的使用
软件钱包普遍使用具有足够熵的值作为种子的伪随机数生成器,足够高的熵能获得相对更高的安全性和可预测难度,但从归根结底,它仍然需要种子来启动,同样的种子+算法就能得到同样的随机数序列,伪随机数的周期循环规律也仍然存在,只是被拉长到了一个足够大的周期,我们可以说它隐患比较小,但不能当它不存在。 伪随机数由于其适用性广,生成速度快等优势在许多场合使用,但在涉及安全的场合,使用伪随机数生成器,可能会带来严重的后果。如TrustWallet在2023年发布公告,其在某些版本的浏览器扩展钱包中,使用了伪随机数生成器 MT19937,但由于其无法提供足够随机性,有生成相同助记词的潜在风险,因此他们披露了这个问题并引导受影响的用户转移资产并更新到新版本。 对安全极致看重的用户,可能对硬件钱包的TRNG仍然不够放心。Keystone 也理解这种担忧,所以也内置了使用骰子创建助记词的功能。这需要你自备一颗赌场级别的骰子(重量分布均匀、透明可观测),将骰子至少投掷50次,将每次骰子的结果输入 Keystone 来获得助记词,为了获得更好的随机性,我们也建议投掷到 99 次以上。
对此感兴趣的用户可以前往 youtube 观看我们的教程: https://www.youtube.com/watch?v=JRzxQmpbIPw
通过支持骰子生成助记词,Keystone 进一步地阐释了 Do not trust,verify 这一区块链价值观,更完全地实现用户的“资产自托管”。
- 不要在家中存放加密货币 379 浏览
- 拥有加密货币会将你的密钥和生活置于风险之中 311 浏览
- Web3 安全指南 1874 浏览
- 比特币是如何运行的 2310 浏览
- 第4章:以太坊钱包 1549 浏览
- 如何在 JavaScript 中生成新的比特币地址 1044 浏览
- 忘记一个简单的钱包助记词如何让你损失数百万美元 1961 浏览
- 长期信任与模拟计算机 1282 浏览
- 加密货币操作安全指南第一部分:私钥安全与网络钓鱼防御 800 浏览
- 理解静默支付(一) 2186 浏览
- 如果一个比特币密钥以“6P”开头,它是什么类型的密钥? 2178 浏览
- 如何将私钥转换为以太坊地址 2894 浏览