密码学基础：配对(Pairings)

这是关于密码学的系列文章中的一篇。如果你是第一读到这篇文章，我强烈建议你从本系列的开篇开始阅读。

我们已经探索了_椭圆曲线_的多种应用——一些简单方案和一些更高级的方案。在研究阈值签名时，我们还引入了多项式。即使发挥最大的创造力，我们仍然可以仅基于这些构造设计出许多协议。

但这并不意味着没有其他_工具_存在。还有一个非常重要的工具需要介绍：配对。

在本文中，我们将定义什么是配对——但不会讨论如何_计算_它们。原因是目前我们还没有定义配对计算所需的数学机制。这可能会在后续文章中探讨，但如果你感兴趣，这里有一份极好的资源可供参考。此外，如果你想在阅读本文后开始尝试配对计算，市面上也有许多库可用！

配对

配对，也称为双线性映射，本质上是一个函数，通常用字母_e_表示。它接受_两个_参数，并生成_一个_输出，如下所示：

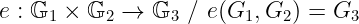
这次我们需要用到集合论中的一些符号，但不会太复杂。

可能最不常见的一个（如果你之前没有接触过太多集合论）是笛卡尔积——用于集合_𝔾₁ × 𝔾_₂。它只是所有形如(G₁, G₂)的元素的集合，其中G₁属于_𝔾_₁，G₂属于_𝔾_₂。

然而，这不是普通的函数。它有一个重要属性：在两个输入上都是_线性_的。这意味着以下所有表达式都是等价的：

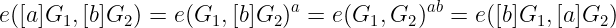
如你所见，我们可以进行这种乘积（更准确地说，群操作）的交换。尽管这个属性乍一看并不起眼，但它实际上非常强大。

配对就像一种搅拌机，因为我们并不太关心_评估_配对表达式时获得的特定值（除非在检查所谓的非退化性时）。相反，我们关心的是某些输入组合产生相同的结果，因为上述的双线性。这正是它们吸引人的地方，我们将在后面看到。

椭圆曲线与配对

注意输入来自笛卡尔积𝔾₁ × 𝔾₂。这是一个相当特殊的集合：𝔾₁和𝔾₂是群，更准确地说，是不相交的群——即它们不_共享_任何元素。形式上，我们说它们的交集为空：

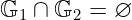
此外，𝔾₁和𝔾₂不仅仅是任何群——它们必须_适合_配对计算。事实证明，椭圆曲线群恰好是一个好选择——在计算效率方面非常出色。因此，我们已经对它们有了很好的理解，这真是一个幸运的巧合！

如果你查阅文献，会发现有些实例中使用的是同一个群两次，而不是两个不相交的群。例如𝔾 × 𝔾。

这些有时被称为自配对，实际发生的是存在一个将_𝔾_₂映射到_𝔾_的函数f——意味着我们可以将_𝔾_₂的元素转换为_𝔾_的元素，并在配对中使用𝔾。

尽管我们不会讨论如何实现这一点，但请记住，配对的正式定义要求群是不相交的。

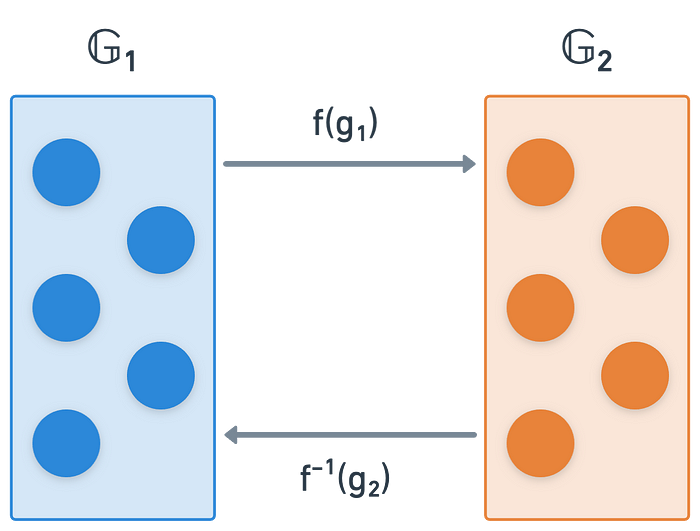
某些函数f允许在群G₁和G₂之间来回移动。

应用

在我们到达"我为什么要学这个"的阶段之前（假设我们还没到那里！），我认为展示_一个应用_是有益的。

尽管我们还不知道如何计算配对，但我们可以理解它们的实用性，因为我们知道它们的属性。

我们不再浪费时间，直接进入正题。

设置

使用椭圆曲线群，甚至是模p整数，可以让你走得很远。但你知道它们都无法为你做的一件事吗？它们不允许你将_身份_用于密码学操作！

砰！麦克风掉落！

身份？你是指我的名字？听起来很疯狂，但可以实现。不过需要一些设置。

要执行这种密码学魔术，我们需要一个受其他方信任的特殊角色——通常称为可信机构。该角色将负责私钥生成，因此也被准确（且非常描述性地）称为私钥生成器（PKG）。

PKG做几件事。首先也是最重要的，他们选择一个主密钥，即一个整数s。他们还选择并公开一些公共参数，我们稍后将定义这些参数。最后，他们选择并公开一个哈希函数H，该函数哈希到𝔾₁。

要获取私钥，Alice必须向PKG请求。为此，她向他们发送她的哈希身份。她的_身份_可以是任何东西——姓名、电子邮件地址、身份证号码，_任何_能唯一标识个人的东西。我们将其表示为ID。她的公钥则是：

收到此值后，PKG将她的私钥计算为：

并将其发送给Alice。

所有这些通信都假设通过安全通道进行。特别是，Alice的私钥不应泄露！

我们的设置完成！Alice拥有她的_私钥_和公钥。她能用这些做什么？

基于身份的加密

假设Alice想为Bob加密消息。她只有他的公钥，因为她知道他的身份（ID）。只需_哈希_它，她就能获得他的公钥：

我们还需要另外几样东西：

• 一个点P ∈ 𝔾₂，用于计算点Q = [s]P，同样在𝔾₂中。由于_s_仅由可信机构知晓，这些点由PKG计算并发布——它们是前面提到的公共参数，我们用_p_表示：

• 我们还需要_另一个_哈希函数H'：

该加密方案采用与椭圆曲线集成加密方案类似的策略：掩蔽。因此，为了加密消息M，Alice遵循以下步骤：

• 她选择一个随机nonce，即一个整数k。
• 用它计算U = [k]P。这将用于稍后重建掩码。
• 然后，使用Bob的公钥（即其身份的哈希值），她计算：

• 她使用该值计算掩码，并将其添加到消息中：

最终的加密消息将是元组(U, V)。

记住_⊕符号表示异或操作。该操作的一个属性是：M ⊕ A ⊕_ A = M。这意味着添加掩码两次可以恢复原始消息。

Bob如何解密？他可以取_U_并简单地_重新计算_掩码。用它，他重新获得原始消息：

但是等等……这两个掩码如何相等？显然，它们看起来不像同一个东西……它们是配对的不同评估！

*恐慌*

别担心——我保证这是有道理的。因为这正是配对的神奇之处：利用它们的_双线性_属性，我们可以证明这两个值是_等价_的：

就这样，仅知道Bob的身份，Alice就可以_专门为他_加密信息——当然，这要归功于配对！

总结一下，以下是该过程的视觉表示

回到配对

好了，现在我们已经看到配对的实际应用，我们有充分的动力去更深入地理解它们的定义。对吧？对吧？

哦，我看到你了

这不会花太长时间——我们只是快速浏览一下使配对成为可能的一些思想。

我们提到𝔾₁和𝔾₂很可能是椭圆曲线群。

那么，我们只需要选择两条不同的椭圆曲线吗？在这种情况下，我们必须确保群是不相交的，这不一定容易；在这种情况下还有其他问题。

使用单个椭圆曲线如何？那么我们将需要两个不同的子群。当我们使用群生成器_G_时，由它生成的群不一定是椭圆曲线群的全部——但_可能_是。这种_包含_关系写作：

这意味着：由G生成的群要么是一个子群，要么是整个椭圆曲线。

我们通常希望由_G_生成的子群的阶尽可能大，以便DLP问题困难。这意味着：

• 如果存在其他子群，它们可能很小。
• 如果⟨G⟩是整个椭圆曲线，则没有其他可用的子群。

我们似乎陷入了一个难题……

扩展曲线

幸运的是，我们的小危机有解决办法。你看，我们的曲线总是在_模q整数_上定义——但如果我们能_扩展_我们使用的可能值呢？

不再仅允许椭圆曲线中的点在_模q整数_中取值：

我们可以使用像_复数_这样的东西，并允许_E_中的点在此集合中取值：

使用复数很有意义：例如，你可以自己验证点_(8, i)_位于以下椭圆曲线上：

域扩展

复数只是一个更一般概念的示例，即域扩展。

域（我们用_F_表示）只是一个具有某些关联操作的集合。这可能会让你想起——与我们系列开始时对群的定义非常相似。

无论形式如何，有一个非常重要的域需要关注：当_q_是素数时的模q整数。

这可能有点误导。最初，我告诉你模q整数是一个群。事实上，如果我们使用单一操作（如加法），它们的行为就像一个群。

更一般地说，它们是一个域，因为它们支持加法、减法、乘法和除法（实际上是模逆元！）。

_域扩展_简单来说是一个包含原域的集合K：

条件是_F_元素之间的操作结果始终位于_F_中，但_绝不_在_K_的其余部分（集合_K - F_中）。

一个众所周知的域扩展当然是复数集。实数作为F，实数之间的操作（加法、减法、乘法和除法）也位于实数(F)中。复数之间的操作可能产生实数，也可能不产生实数。

这为什么重要？假设我们在模_q_整数上定义一个曲线。我们得到一堆点，可以表示为：

如果我们_扩展_基域（模_q_整数），则会出现新的有效点，同时_保留_旧点。即：

因此，_新的子群_出现，我们还有额外的好处：保留在基域上定义的原子群。

当我们选择_适当的_域扩展时，神奇的事情发生了：我们得到_大量_与⟨G⟩_同阶_的子群。这些群几乎是不相交的：它们只共享单位元，O。所有这些子群的集合就是所谓的挠群。

曲线E/F_11: y² = x³ + 4的3-挠群。每个蓝色框是一个子群，连同O，它是所有子群的共同元素——因此它被描绘在中心。

好了，我们就此打住。本节的目标只是介绍配对输入的一般概念。然而，如果不深入探讨这个主题，我们就无法进一步阐述，而这超出了这篇介绍性文章的范围。

再次推荐这本书以获取更详细的解释——它本身也引用了一些优秀的进阶资源。

这里的重要思想是，配对计算绝非微不足道。如果你有兴趣让我在后续文章中进一步扩展这个主题，请告诉我！

总结

尽管我们尚未深入探讨配对的领域，但这个简单的介绍让我们理解了基于配对方法的工作原理。一切都取决于我们在文章开头看到的_双线性_属性。

关键要点是：

配对就像搅拌机，我们关心的是两组不同输入的计算结果是否相同

我们可能会在以后探讨配对计算。我认为先看一些应用会更有成效。

因此，我们将在系列的下一部分中探讨更多配对应用。到时见！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～