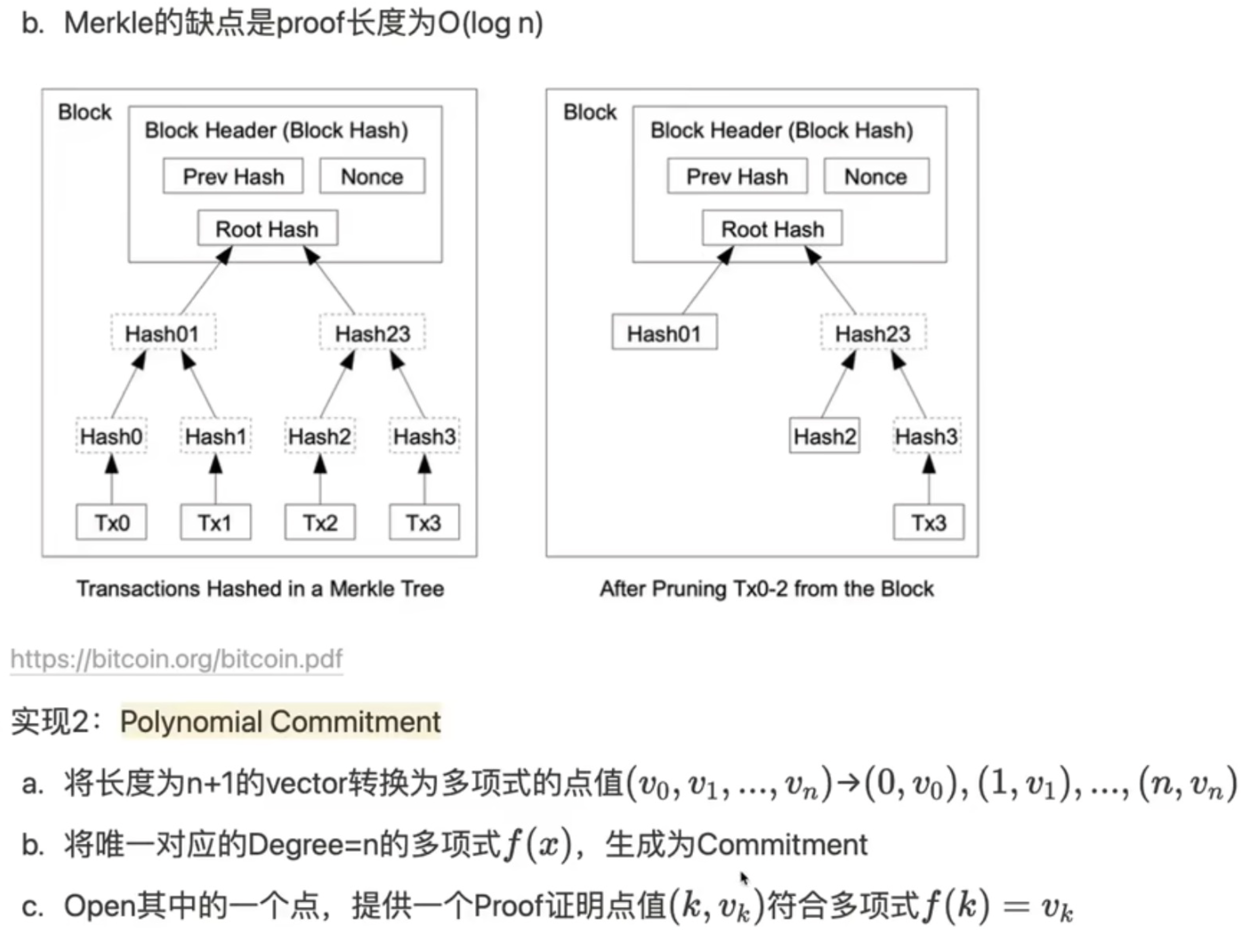
KZG 知识点更加精炼的总结
- 杜满想Elvin
- 发布于 2024-09-20 17:33
- 阅读 3654
Trusted Setup其实就是生成一个非对称加密的私钥,即s;然后生成一系列的公钥,即g^(s^i), i = 0....n;其中g是椭圆曲线中的生成元; i是从0到n的整数,n是多项目的degree。其中的s必须销毁,谁都不能知道;只保留下来一系列的公钥;以太坊基金会已经生成了4组这类的公钥对
主要内容来自于Qi Zhou大神视频
生成commitment

Trusted Setup其实就是生成一个非对称加密的私钥,即s;然后生成一系列的公钥,即g^(s^i), i = 0....n;其中g是椭圆曲线中的生成元; i是从0到n的整数,n是多项目的degree。其中的s必须销毁,谁都不能知道;只保留下来一系列的公钥;以太坊基金会已经生成了4组这类的公钥对供社区使用;
C即commitment,其实就是多项式的 系数a_i 乘 对应的公钥,然后把相乘的结果相加,值就是整个多项式的承诺,就是一个椭圆曲线的一个点;
因为prover知道系数a,所以选择一组以太坊提供的公钥对,就可以得出一个多项目的承诺了;
多项式的系数a,就是多项目的知识,知道了一个多项目的系数,就知道了多项目;
我们知道,从一堆数据中可以得出一个多项式的点值形式;比如把一个文件分成4份,每份大小8bite;选择x轴从0开始。例如:[0, 3], [1, 22], [2, 77], [3, 98]; 把数据的点值形式根据拉格朗日插值方式,或者FFT方式转化成多项目,从而得到多项式的系数a_i;
根据这些系数a_i和一组以太坊提供的公钥对,就可以得出这个多项目的承诺了;这个多项目代表的就是这个文件的commitment,可以看作是一个文件内容的merkle root(merkle承诺);
生成proof

用户发起一个挑战x_i(x的索引位置),prover计算出相对应的y_i,并且给出一个proof,这个proof类似于merkel proof,用于证明prover给出的y_i是符合 commitment的,是没有作恶的;
proof计算的方式主要分为两步: 第一步:把f(x) 多项式分解成为 f(x) = t(x)h(x),即两个多项式相乘; 第二步:因为t(x)和h(x)都是秘密,不可以给用户;prover会对t(x)和h(x)两个多项式和Trusted Setup得到的公钥对进行相乘,然后相加,再次得到两个多项式的commitment;这就是y_i的proof;
Verify
因为椭圆曲线无法处理乘法运算,所以我们根据双线性映射,根据下面的共识进行verify;
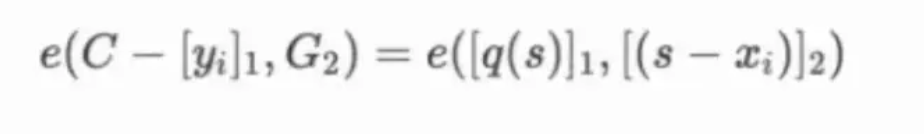
总结
来自于另一个大神的视频
Plonk和ZKG的对比
对比Plonk的Trusted setup和KZG的Tursted Setup,我们知道plonk的setup有两个输入:一个是私钥s;另一个是挑战alpha,同时要隐藏着两个输入;同时产出proving key和verify key;
而KZG的setup只有一个输入,就是私钥s;用户的挑战alpha(即x_i)是全网都可以知道的数;
同时可以知道,ZKG和merkle root的效果是差不多的,用于保证prover没有修改数据(保存了数据)或者证明y_i是否是存储数据的一部分或者数据位置x_i;其中没有太多零知识证明证明中的零知识性;只是多了两个优点:
- commitment只有49个bit,且不管叶子节点的数量是多少,都是恒定48 bit;
- 可以用多项式的特性做数据冗余和恢复;
而Plonk则复杂很多,能达到输出的结果一定是按照程序逻辑来运行得出来的结果,prover必须按照程序步骤,一步步计算出来的结果,不能作恶;
- ZK编年史:哈希登场 155 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 363 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 289 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 380 浏览
- Zcash:比特币遗忘的隐私 435 浏览
- ZK编年史:计算模型 301 浏览
- lambdaworks 2026 年更新路线图和优先级 367 浏览
- Lean 4 工程化入门:Elan 工具链配置与 Lake 包管理实战 601 浏览
- 2026年构建机构级DeFi平台真正需要什么 909 浏览
- zkMesh:2026年1月回顾 453 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 650 浏览
- Zcash 的时代到来了 780 浏览

