STARKs，第二部分：感谢老天爷，今天是FRI日

特别感谢 Eli Ben-Sasson 的持续帮助和解释，以及 Justin Drake 的审阅。

在本系列的最后一部分中，我们讨论了如何可以创建一些非常有趣的计算的简洁证明，例如证明你计算了第百万个斐波那契数，使用的技术涉及多项式的组合和除法。然而，这依赖于一个关键要素：证明至少大多数给定的大集合的点都在同一个低度多项式上。这个问题称为“低度测试”，它可能是协议中最复杂的部分。

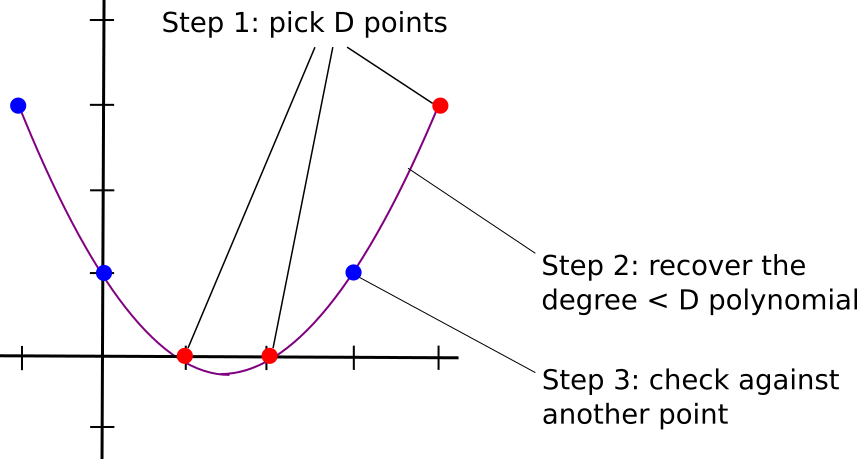
我们将首先再一次重述问题。假设你有一组点，并且你声称它们都在同一个度数小于 D 的多项式上（即，deg<2 意味着它们在同一条直线上，deg<3 意味着它们在同一条直线或抛物线上，等等）。你想创建一个简洁的概率性证明，证明这确实是正确的。

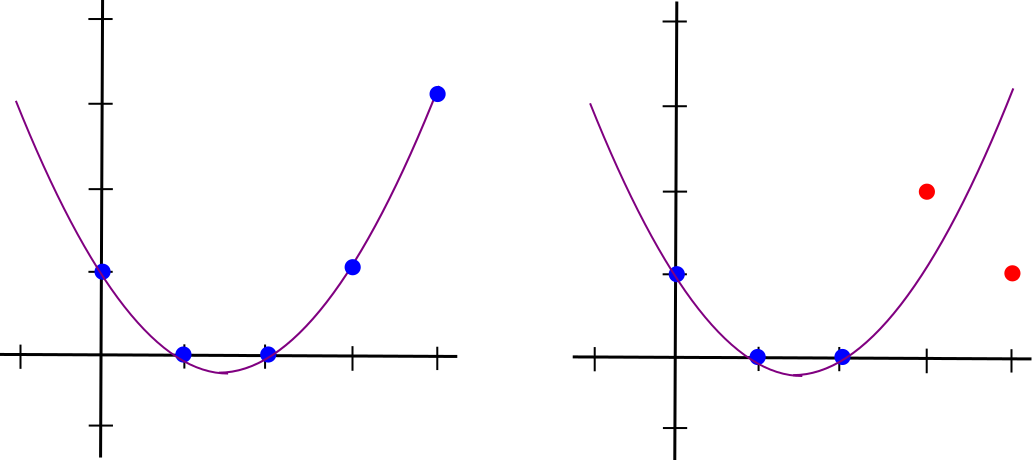
如果你想验证这些点是否_都_位于同一个度数 <D 的多项式上，你实际上需要检查每一点，因为如果你未能检查到一个点，总会存在一定的概率该点可能不在多项式上，即使其他所有点都在。但是你_可以_做的是_概率性地检查_至少某个部分（例如，90%）的点在同一个多项式上。

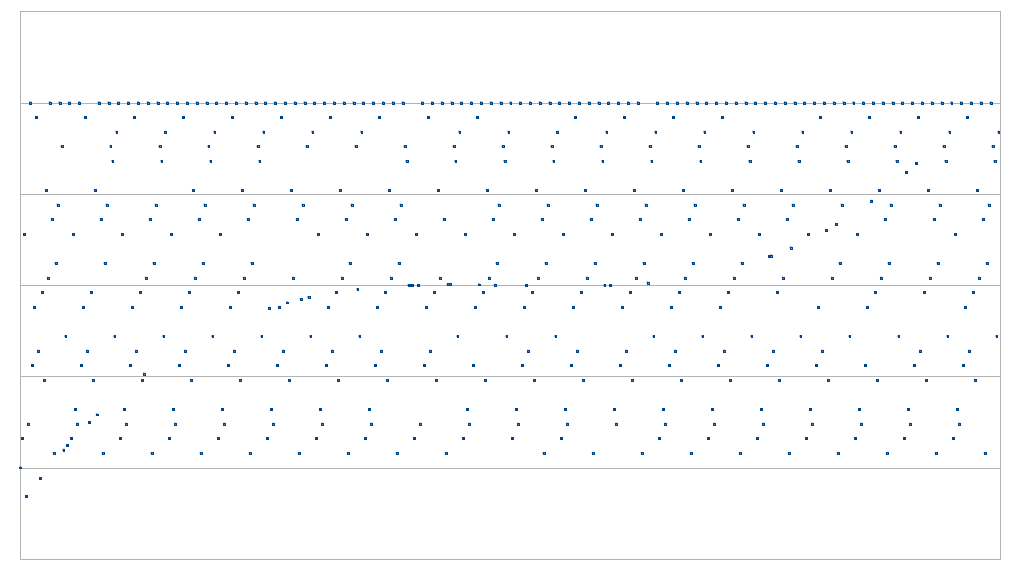
如果你有能力查看_每_个点在多项式上，那么问题就简单了。但是，如果你只能查看几个点——也就是说，你可以要求任何特定的点，而证明者有义务在协议中提供该点的数据，但查询的总数是有限的？那么问题就变成了，你需要检查多少个点才能以某种给定的确定性告诉你？

显然，D 点不足够。D 个点正好是定义一个度数 <D 多项式所需的，因此_任何_一组你收到的点都将对应于_某_个度数 <D 的多项式。然而，如上图所示，D+1 个点或更多确实会给出某种指示。

使用 D+1 次查询检查给定值集是否位于同一个度数 <D 的多项式上的算法并不复杂。首先，选择 D 个点的随机子集，并使用诸如拉格朗日插值（搜索“Lagrange interpolation” 这里以获取更详细的描述）来恢复通过它们的唯一度数 <D 的多项式。然后，再随机抽取一个点，并检查它是否在同一多项式上。

请注意，这只是一个接近性测试，因为总有可能大多数点在同一个低度的多项式上，但少数不在，而且 D+1 的样本完全错过了那些点。然而，我们可以推导出，如果少于 90% 的点在同一个度数 <D 的多项式上，则测试将以高概率失败。具体来说，如果你进行 D+k 次查询，并且至少有部分 p 的点不在与其他点相同的多项式上，则测试只有以 (1−p)k 的概率通过。

但是，如果像前一篇文章中的例子那样，D 非常高，而你希望用少于 D 次查询验证一个多项式的度数，怎么办？这当然是不可能直接做到的，因为上述简单的论证（即任何 k≤D 个点都至少在一个度数 <D 的多项式上）引出了这个问题。然而，间接地提供辅助数据，并通过此实现巨大效率增益，是完全可能的。这正是新的协议如FRI（“快速 RS IOPP”，RS = “Reed-Solomon”，IOPP = “交互式预言机接近性证明”）和类似的早期设计，称为概率可检查的接近性证明（PCPPs）所尝试实现的。

初步了解亚线性

为了证明这至少是可能的，我们将从一个相对简单的协议开始，尽管权衡不是很好，但仍然实现了亚线性验证复杂度——即，你可以用少于 D 次查询证明与度数 <D 多项式的接近性（并且，从这个意义上讲，验证证明需要的计算也少于 O(D)）。

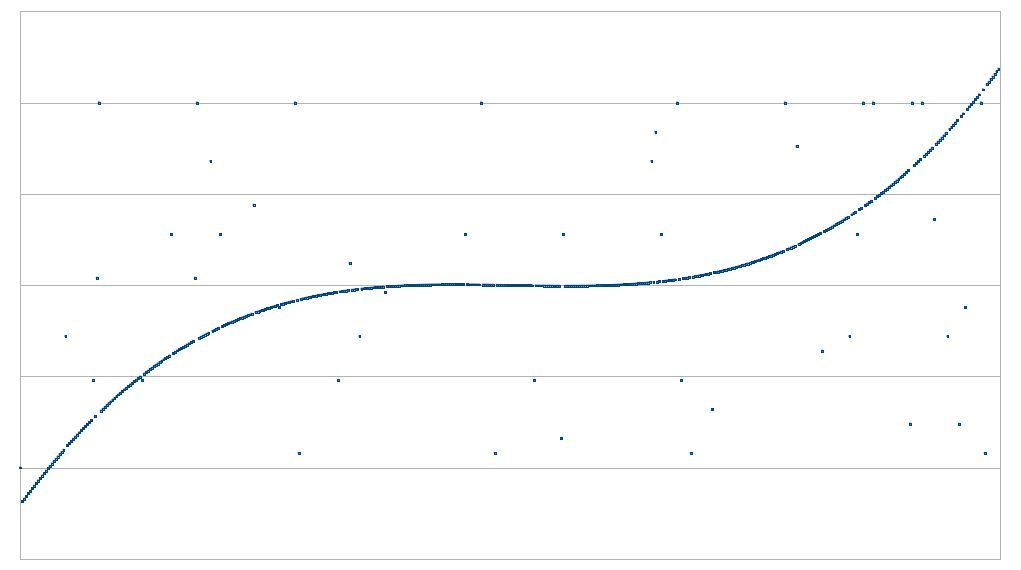
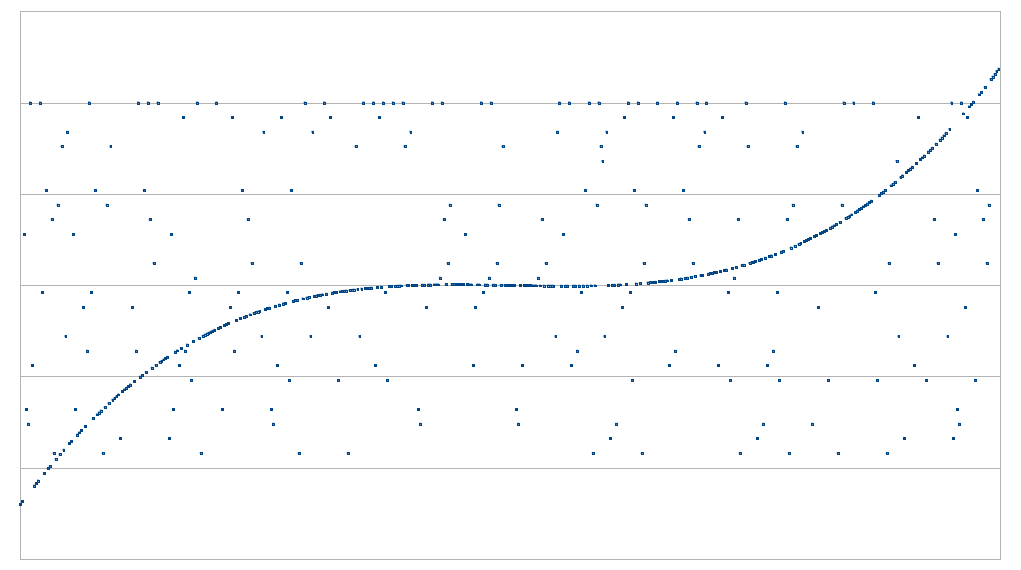
其思路如下。假设有 N 个点（我们说 N = 10 亿），它们都位于一个度数 < 1,000,000 的多项式 f(x)。我们找到一个双变量多项式（即，像 1+x+xy+x5⋅y3+x12+x⋅y11 这样的表达式），我们将其记为 g(x,y)，使得 g(x,x1000)=f(x)。这个可以通过以下方式完成：对于 f(x) 中第 k 个度数项（例如，1744⋅x185423），我们将其分解为 xk%1000⋅yfloor(k/1000)（在本例中，1744⋅x423⋅y185）。你可以看到，如果 y=x1000，则 1744⋅x423⋅y185 等于 1744⋅x185423。

在证明的第一阶段，证明者承诺（即，制作一个 Merkle 树）对 g(x,y) 在整个方形区域 [1...N]x{x1000:1≤x≤N} 的评估——也就是说，对于列的所有 10 亿个 x 坐标，以及对于行的所有 10 亿个相应的_千次方_的 y 坐标。该方形的对角线表示 g(x,y) 的值，该值的形式为 g(x,x1000)，因此对应于 f(x) 的值。

然后，验证者随机选取几十行和列（如果我们想要非交互式证明，可能可以使用方形的 Merkle 根作为伪随机数源），对于每行或列，验证者要求获得该行和列上的示例，例如 1010 个点，在每种情况下确保所要求的点之一位于对角线上。证明者必须回复这些点，以及证明它们是证明者承诺的原始数据中一部分的 Merkle 分支。验证者检查 Merkle 分支是否匹配，并且证明者提供的点是否确实对应于度数为 1000 的多项式。

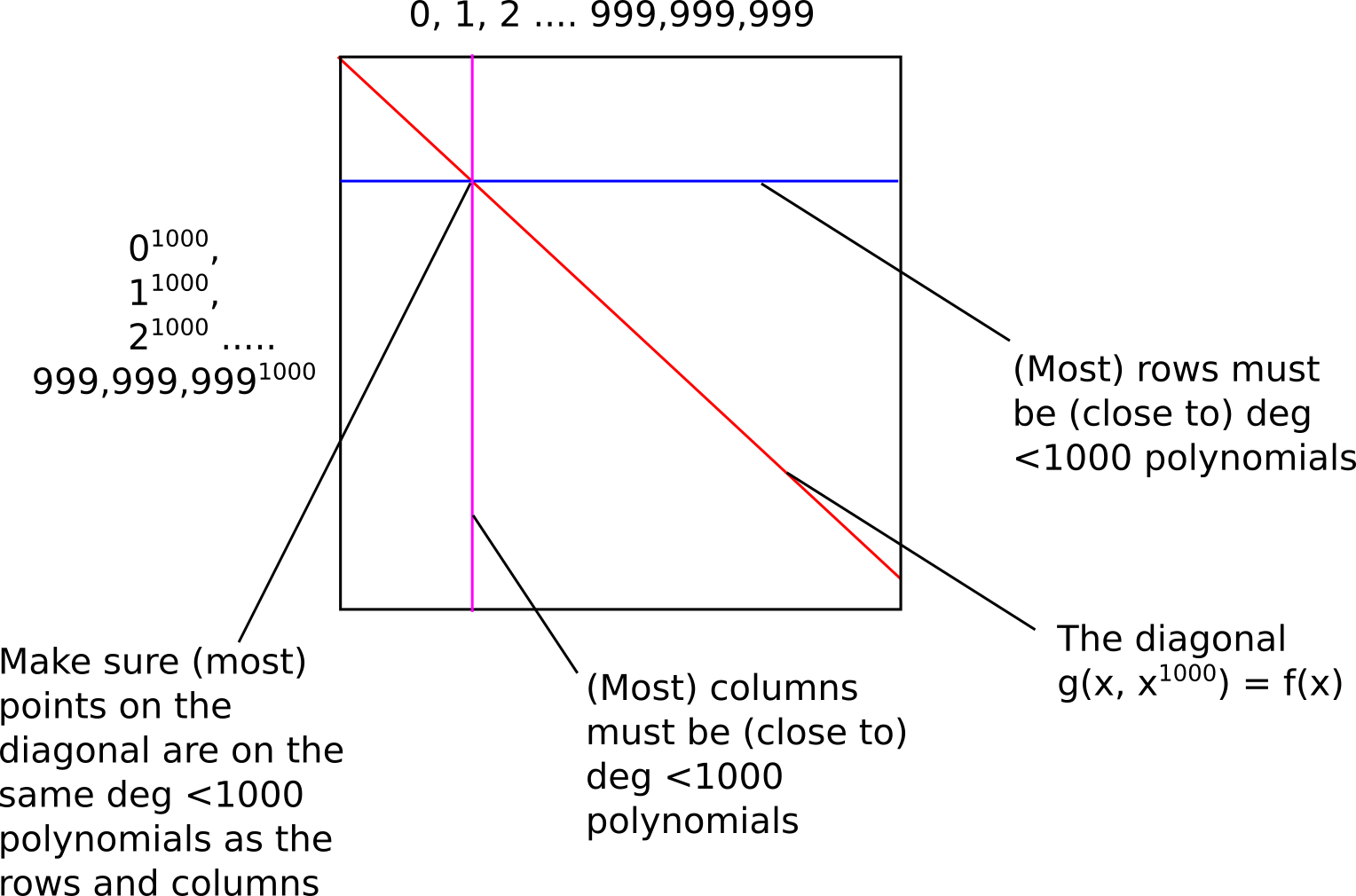
这只给验证者一个证明，表示（i）大多数行主要由度数 <1000 的多项式上的点填充，（ii）大多数列主要由度数 <1000 的多项式上的点填充，以及（iii）对角线大部分在这些多项式上。因此，这使得验证者相信对角线上的大多数点实际上确实对应于一个度数 <1,000,000 的多项式。

如果我们选择三十行和三十列，则验证者需要访问总计 1010 点 ⋅ 60 行+列 = 60600 点，少于最初的 1,000,000，但没有减少太多。就计算时间而言，插值度数 <1000 的多项式将有其自身的开销，不过，由于多项式插值可以做到亚二次，因此整体算法的验证仍然是亚线性的。_证明者_的复杂性更高：证明者需要计算和承诺整个 N⋅N 矩形，这总共需要 1018 的计算努力（实际上略多，因为多项式评估仍是超线性的）。在所有这些算法中，证明一个计算通常要比直接运行它复杂得多；但正如我们将看到的，那些开销并不一定得那么高。

模块数学插曲

在我们进入更复杂的协议之前，我们需要稍微转向模算术的世界。通常，当我们处理代数表达式和多项式时，我们正在处理常规数字，而算术运算，使用操作符 +, -, ⋅, /（以及幂运算，实际上是重复的乘法），是以我们从学校学到的方式进行的：2+2=4，72/5=14.4，1001⋅1001=1002001，等等。然而，数学家们意识到，这些定义加法、乘法、减法和除法的方式并不是定义这些运算的_唯一_自洽方式。

定义这些运算的另一种方式最简单的例子就是模算术，定义如下。% 操作符的意思是“取余数”：15, 53, 等等（注意答案总是非负的，因此例如 -1）。对于任何特定的素数 p，我们可以重新定义：

x+y⇒(x+y) % p

x⋅y⇒(x⋅y) % p

xy⇒(xy) % p

x−y⇒(x−y) % p

x/y⇒(x⋅yp−2) % p

上述规则都是自洽的。例如，如果 p=7，则：

• 5+3=1（因为 8 % 7=1）
• 1−3=5（因为 −2 % 7=5）
• 2⋅5=3
• 3/5=2（因为 (3⋅55) % 7=9375 % 7=2）

更复杂的恒等式，例如分配律也成立： (2+4)⋅3 和 2⋅3+4⋅3 的结果均为 4。即使像 (a2−b2) = (a−b)⋅(a+b) 这样的公式在这种新的算术中也仍然是正确的。除法是最困难的部分；我们无法使用常规的除法，因为我们希望值始终保持整数，而常规除法经常给出非整数的结果（例如 3/5）。上面除法公式中有趣的 p−2 指数是使用Fermat 小定理（该定理声称对于任何非零的 x<p，成立 xp−1 % p=1）绕过这个问题的结果。这意味着 xp−2 生成的数字，如果再乘以 x 一次，等于 1，因此我们可以说 xp−2（这是一个整数）等于 1x。一个稍微复杂但更快的方法来评估这个模除法运算符是扩展的欧几里得算法，在 python 中这里实现。

通过模数学我们创建了一个全新的算术系统，因为它在所有与传统算术相同的自洽方式中都是自洽的，我们可以讨论这个领域中所有与“常规数学”相关的结构，包括多项式。密码学家喜欢在模数学（或更一般地说，“有限域”）中工作，因为作为任何模算术计算结果生成的数字都有界限——无论你做什么，数值不会“超出”集合 {0,1,2...p−1}。

Fermat 小定理还具有另一个有趣的结果。如果 p−1 是某个数字 k 的倍数，那么函数 x→xk 的“像”值是有限的——即，该函数只能给 p−1k+1 个可能的结果。例如， x→x2 当 p=17 时只有 9 个可能的结果。

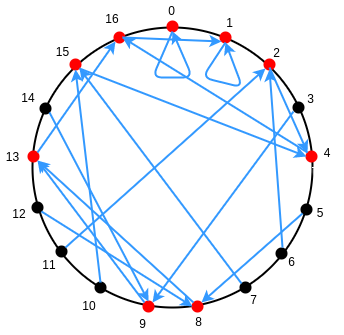
随着更高指数的出现，结果更加明显：例如，x→x8 当 p=17 时只有 3 个可能的结果。当然，x→x16 当 p=17 时只有 2 个可能的结果：对于 0，它返回 0；对于其他所有值，它返回 1。

现在提高一点效率

现在让我们转向一个略微复杂的协议版本，其适度目标是将证明者的复杂性从 1018 降低到 1015，然后降低到 109。首先，不再使用常规数字，而是通过使用模算术进行多项式的接近性检查。如我们在前一篇文章中看到的，我们需要这样做以防止 STARKs 中的数字膨胀到 200,000 位。然而，在这里，我们将利用某些模幂运算的“小像”特性作为副作用，使我们的协议更加高效。

具体来说，我们将使用 p= 1,000,005,001。我们选择这个模数，因为 (i) 它大于 10 亿，我们需要至少 10 亿以便检查 10 亿个点，(ii) 它是素数，以及 (iii) p−1 是 1000 的偶数倍。幂运算 x1000 的像值的大小为 1,000,006——也就是说，幂运算只会给出 1,000,006 个可能的结果。

这意味着“对角线”（x, x1000）现在成为了一个带有环绕的对角线；因为 x1000 只能取 1,000,006 个可能的值，因此我们只需要 1,000,006 行。因此，g(x,x1000) 的完整评估现在只有大约 1015 个元素。

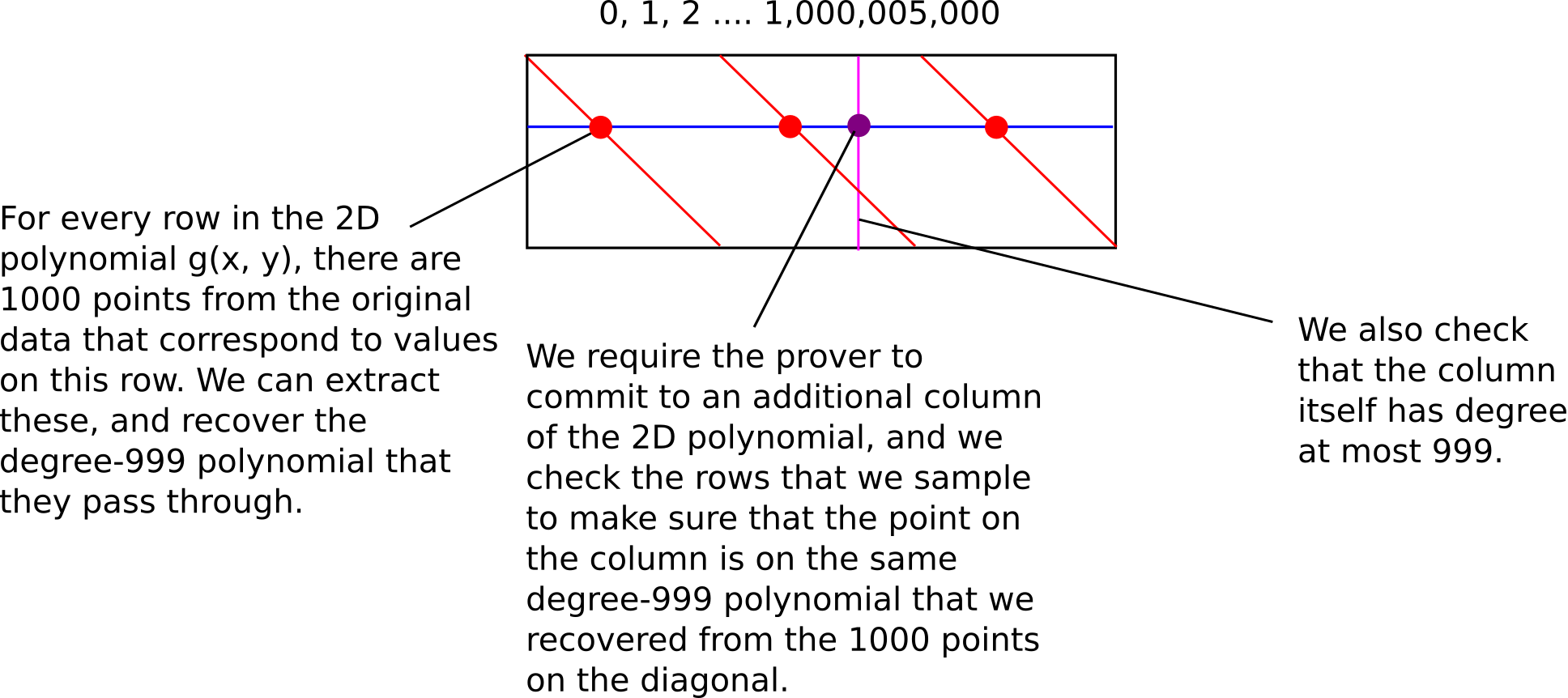
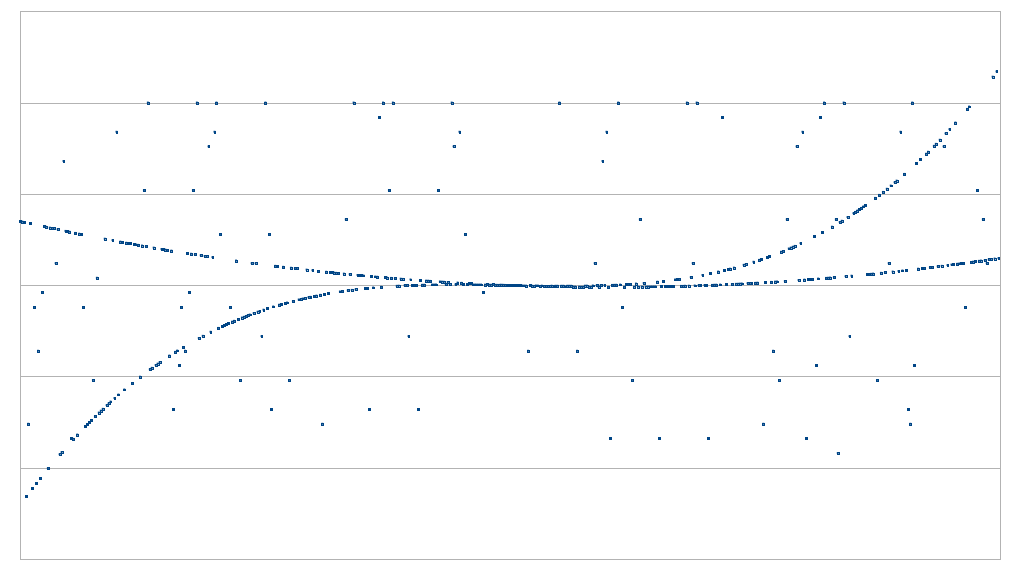
事实证明，我们可以更进一步：我们可以让证明者仅对 g 的单一列进行承诺。关键的技巧是原始数据本身已经包含位于任何给定行的 1000 个点，因此我们可以简单地抽取这些点，推导出它们所在的度数 <1000 的多项式，然后检查列上对应的点是否也在同一个多项式上。然后我们检查该列本身是否是一个 <1000 的多项式。

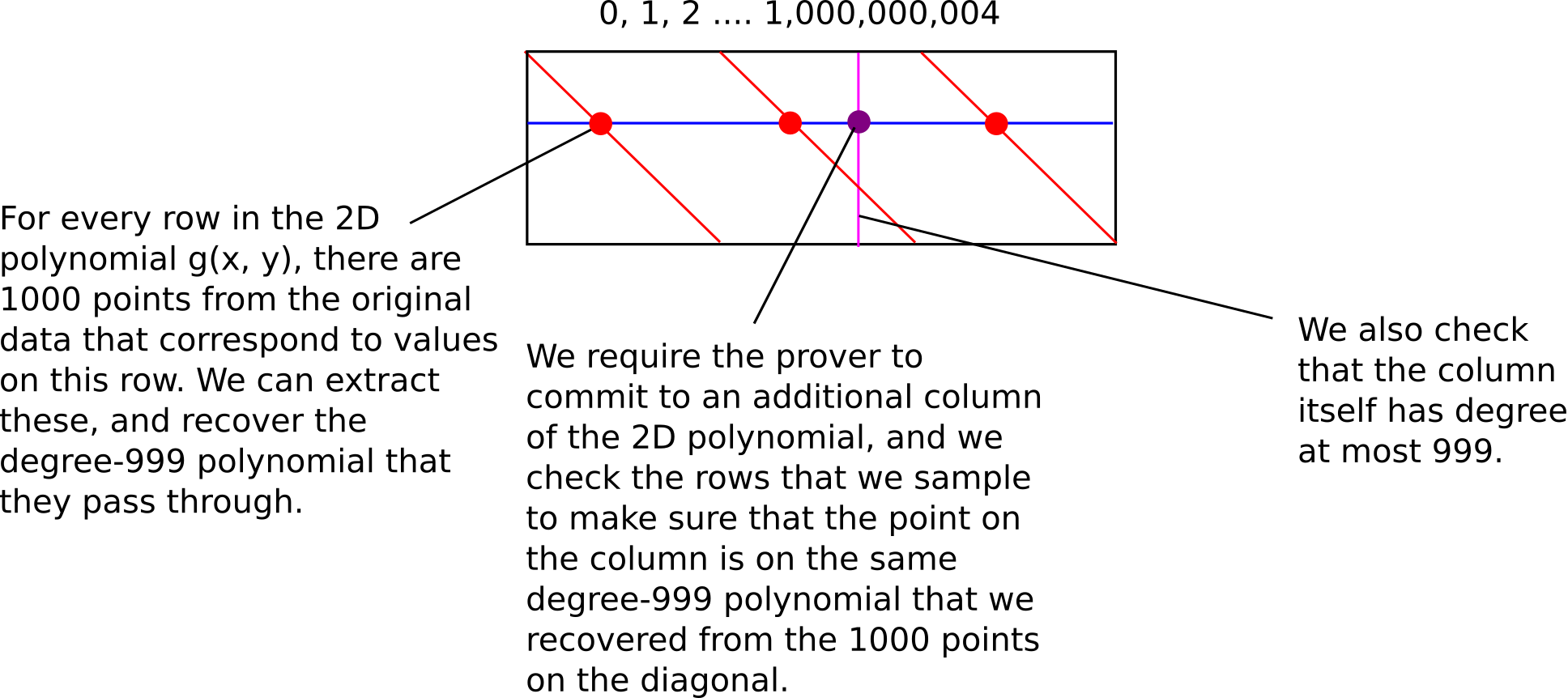
验证者复杂度仍然是亚线性的，但证明者复杂度现在下降到 109，使得它在查询数量上是线性的（不过在实践中由于多项式评估的开销仍然是超线性的）。

更高的效率

证明者的复杂度现在基本上达到了最低限度。但我们仍然可以进一步降低验证者复杂度，从二次降到对数。我们怎么做到这一点？就是通过使算法递归。我们首先从上面的最后协议开始，但是不再试图将多项式嵌入到一个 x 和 y 的度数相等的二维多项式中，而是将多项式嵌入到一个二维多项式中，在该多项式中 x 的度数上限是一个小的常数值；为了简单起见，我们甚至可以说这个常数必须为 2。也就是说，我们将 f(x)=g(x,x2) 表达，确保对我们采样的每行，只需检查 3 个点（2 个来自对角线加 1 个来自列）。

如果原始多项式的度数 <n，则行的度数 <2（即行是直线），而列的度数 <n2。因此，我们现在拥有的是一个线性时间过程，将证明多项式的接近性的问题转化为证明一个度数 <n2 的多项式的接近性的问题。此外，还需要承诺的点的数量，因此，证明者的计算复杂性每次减少 2 倍（Eli Ben-Sasson 喜欢将这个 FRI 的特性与快速傅里叶变换进行比较，关键的不同在于，与 FFT 不同，递归的每一步只引入一个新的子问题，而不是分支到两个）。因此，我们可以继续在前一轮协议中创建的列上使用该协议，直到该列缩小到我们可以直接检查的程度；总复杂性大约是 n+n2+n4+...≈2n。

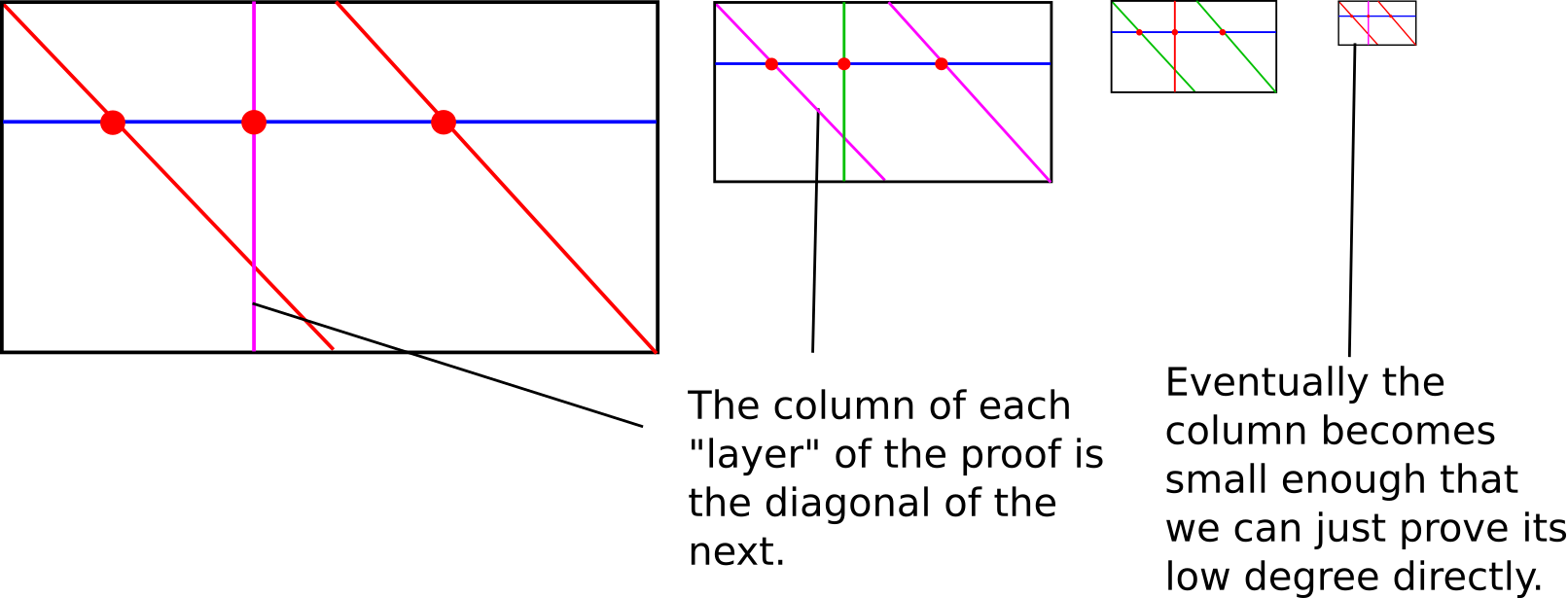
实际上，该协议需要重复多次，因为仍然有相当大的概率攻击者会欺骗_一个_回合的协议。然而，即便如此，证明的大小也不算太大；验证复杂度在度数上是对数的，虽然如果计算 Merkle 证明的大小，则会增加到 log2⁡n。

“真实”的 FRI 协议还具有其他一些修改；例如，它使用二进制伽罗瓦域（另一种奇怪的有限域；基本上，与我在这里中讨论的 12 次扩展域相同，但素数模数是 2）。行的指数通常也是 4，而不是 2。这些修改提高了效率，并使系统更容易在其上构建 STARKs。然而，这些修改并不有助于理解算法是如何工作的，如果你真的想的话，你当然可以使用这里描述的简单基于模算术的 FRI 来构建 STARKs。

可靠性

我提醒你，计算可靠性——即，确定在给定数量的检查中，一个优化生成的假证明通过测试的概率有多低——仍然是这个领域中一个“有龙出现的地方”。对于简单的测试，你取 1,000,000 +k 个点，有一个简单的下限：如果给定的数据集具有这样的属性，即对于任何多项式，至少部分 p 的数据集不在这个多项式上，则对该数据集的测试最多将以 (1−p)k 的概率通过。然而，即便如此，这也是一个非常悲观的下限——例如，不可能同时接近_两个_低度多项式超过 50%，并且选择的前几个点是最集中的点的概率相当低。对于完整的 FRI，还涉及各种特定类型攻击的复杂性。

这里有一篇 Ben-Sasson 等人最近的文章，描述了 FRI 在整个 STARK 方案中的可靠性属性。一般来说，“好消息”是，这似乎表明，为了通过 STARK 中的D(x)⋅Z(x)=C(P(x)) 检查，一个无效解的 D(x) 值以某种意义上需要是“最坏情况”——它们需要最大程度地远离任何有效多项式。这意味着我们不需要检查_那么_大的接近性。有证明的下限，但这些下限会暗示实际 STARK 的大小需要在 ~1-3 兆字节；推测但未证明的更强的下限将减少所需的检查数量4倍。

这个系列的第三部分将处理构建 STARKs 中的最后一个主要挑战：我们如何实际构造约束检查多项式，以便我们能够证明关于任意计算的断言，而不仅仅是一些斐波那契数。

• 原文链接： vitalik.eth.limo/general...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～