优化Barrett约减：更严格的界限消除冗余减法 - ZKSECURITY

Barrett 约简是一种广泛使用的，用于对一个值进行模 m 约简的算法。我们在 Rust p256 crate 审计 期间进行的分析表明，Barrett 约简的误差界限可以比传统认为的更紧。对于密码学中使用的大多数模数（例如，NIST 曲线），商的近似误差最多为 1（而不是 2）。这种改进实际上消除了第二次减法的需求。通过采用这种优化，RustCrypto p256 在标量乘法中实现了 14% 的性能提升。

什么是Barrett约简？

Barrett 约简是一种有效计算除法运算的余数（即，模运算），xmodm 的方法，而无需执行实际的除法。

我们想要计算 r=xmodm，它可以表示为 x=q⋅m+r，其中 q 是商，r 是余数。在实践中（例如，密码学领域算术），模数 m 可以是使用 k 个 limb 表示的大整数。每个 limb 都是一个 32 位或 64 位的值（取决于机器字），使得基数 b=232 或 264。在实践中，值 x 是一个 2k-limb 整数，因为它是由两个 k-limb 整数的乘法产生的。

计算 r 的一种方法是首先计算 q 为：

q=⌊x/m⌋

一旦确定了 q，就可以将 r 计算为 r=x−q⋅m。Barrett 约简提供了一种更有效的方法来近似 q，避免了直接除法的需求，因为直接除法的计算成本很高。

首先，让我们将上面的公式重写为：

q=⌊x/m⌋=⌊xm⋅b2kb2k⌋=⌊xm⋅b2kbk+1⋅bk−1⌋=⌊b2km⋅xbk−1⋅1bk+1⌋

到目前为止，我们的计算是精确的。但是，我们将通过计算以下内容来近似 q，而不是精确地计算 q：

q~=⌊⌊xbk−1⌋⋅⌊b2km⌋bk+1⌋

这允许我们预计算 μ=⌊b2km⌋ 并将上述公式重写为：

q=⌊⌊xbk−1⌋⋅μbk+1⌋

注意：⌊⋅bk−1⌋ 和 ⌊⋅bk+1⌋ 都可以使用右移快速计算。

由于这两个近似值可能小于它们的精确计算值，因此我们有 q~≤q。传统分析表明 q~∈[q−2,q]（我们将在分析部分中详细说明）。这意味着近似商 q~ 最多比真实商 q 小 2。

计算 r，其中 x≈q~⋅m+r

如果我们精确地计算了 q，我们将简单地计算：

r=x−q⋅m

由于 r∈[0,m)，因此只有 m 的比特长度参与该减法。因此，我们可以通过仅涉及最低有效 bk 位来更快地计算它：

r=x−q⋅mmodbk=(xmodbk)−(q⋅mmodbk)

（其中模 bk 可以有效地计算）

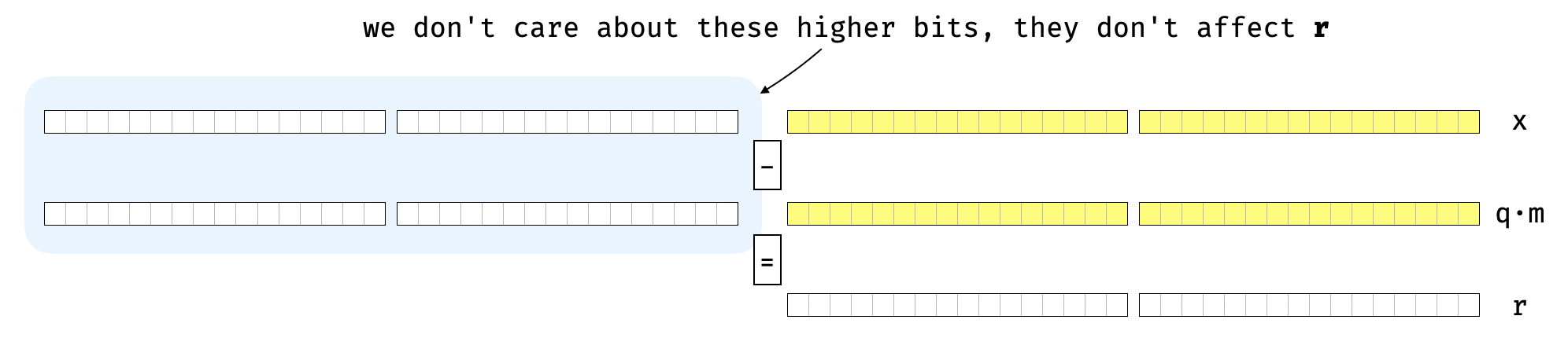
但是，请记住，我们已经计算了 q 的近似值 q~，其中 q~∈[q−2,q]。

我们知道以下情况之一：

1. r=x−q~⋅m
2. r=x−(q~+1)⋅m
3. r=x−(q~+2)⋅m

为了计算 r，我们首先计算情况 1。如果结果不小于 m，我们减去 m 一次或两次以使其进入正确的范围。

这意味着我们可能不会立即得到 r~=x−q~⋅m<bk。相反，该值可能大 m 或 2m 倍。

由于 m<bk，我们知道 2⋅m<2⋅bk。这允许我们对近似值进行上限约束：

r≤r~≤r+2m<bk+2⋅bk<bk+1

然后，我们可以更有效地计算 r~：

r~=((xmodbk+1)−(q~⋅mmodbk+1))modbk+1

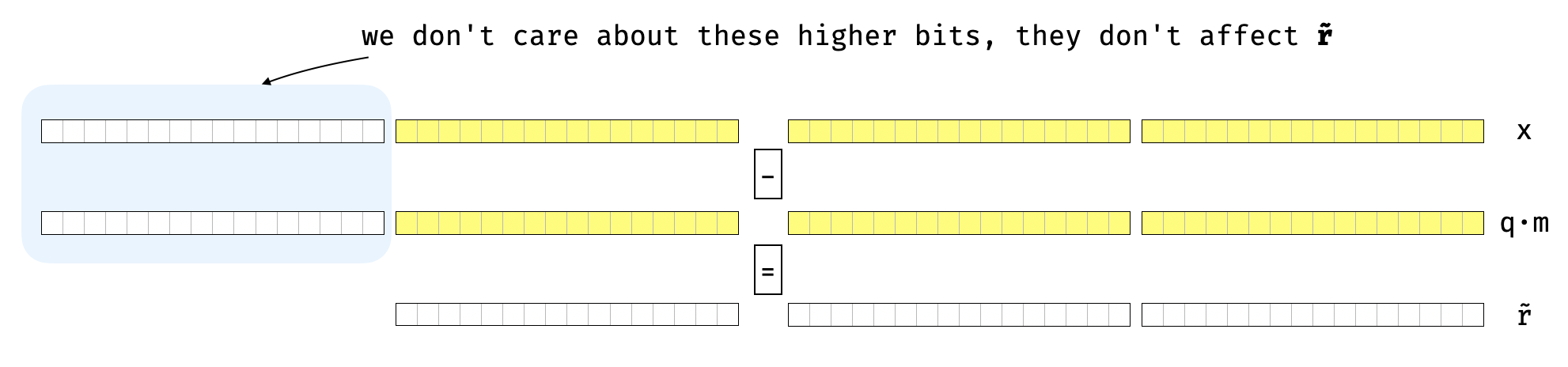
同样，modbk+1 运算在二进制机器上非常高效。

我们最终得到 应用密码学手册，第 14 章 中描述的算法。上面概述的步骤与书中详细描述的过程密切相关。

来源：应用密码学手册，第 14 章

更紧密的界限分析

q~ 的界限直接决定了 r 需要减去 m 多少次才能落在正确的范围内。传统上，已知界限为 q~∈[q−2,q]。在本节中，我们将展示对于实践中几乎所有的模数，更紧密的界限成立：q~∈[q−1,q]。

请记住

q=⌊xm⌋

q~=⌊⌊xbk−1⌋⋅⌊b2km⌋bk+1⌋

由于 q~ 是从 xm 的截断近似值派生的，因此它自然满足 q~≤q。

我们表示 α=xmodbk−1，其中 α<bk−1。表示 β=b2kmodm，其中 β<m。然后我们可以删除 floor 运算：

⌊xbk−1⌋=x−αbk−1

⌊b2km⌋=b2k−βm

然后我们可以简化 q~：

q~=⌊⌊xbk−1⌋⋅⌊b2km⌋bk+1⌋=⌊x−αbk−1⋅b2k−βmbk+1⌋=⌊(x−α)⋅(b2k−β)m⋅b2k⌋=⌊xm−α⋅b2k+β⋅(x−α)m⋅b2k⌋

我们用 z 表示红色部分（注意 z≥0）。然后我们有 q~=⌊xm−z⌋。根据 floor 函数不等式 ⌊x⌋+⌊y⌋+1≥⌊x+y⌋，我们有：

⌊xm−z⌋+⌊z⌋+1≥⌊(xm−z)+z⌋=⌊xm⌋=q

也就是说 q~+⌊z⌋+1≥q。

z 的界限是分析 q~ 的界限的关键。如果我们能证明 0≤z<2，那么我们将有 ⌊z⌋≤1，最终 q~+2≥q~+⌊z⌋+1≥q。让我们分析 z 的界限。

证明 q~∈[q−2,q]

我们有：

z=α⋅b2k+β⋅(x−α)m⋅b2k<bk−1⋅b2k+β⋅b2km⋅b2k=bk−1+βm

我们知道 bk−1<m （因为 m 是 k-limb）并且 β<m。然后我们有：

z<bk−1+βm<m+mm=2

因此：

⌊z⌋≤1

这正是我们想要的。因此，我们得出结论 q~+2≥q~+⌊z⌋+1≥q。

实践中更紧密的界限：q~∈[q−1,q]

我们已经证明在所有情况下 q~∈[q−2,q]。但是，这是一个宽松的界限。在这里，我们声称对于实践中几乎所有的模数 m，我们有一个更紧密的界限：z<1，因此 q~+1≥q~+⌊z⌋+1≥q。

让我们检查哪些模数 m 满足这个更紧密的界限。回想一下 z<bk−1+βm，因此如果以下情况成立，则 z<1 成立：

bk−1+βm≤1

这意味着：

bk−1+β≤m

进一步：

β≤m−bk−1

也就是说，如果 β 不大于 m−bk−1，那么 z<1，因此 q~∈[q−1,q]。我们可以将其形式化为更紧密的界限标准：

给定一个模数 m，如果 β≤m−bk−1 (其中 β=b2kmodm)，则 q~∈[q−1,q]。

值得注意的是，β=b2kmodm 落在 [0,m) 范围内。在实践中，当 b 为 232 或 264，并且 m 接近 bk 时，值 m−bk−1 非常接近 m。

对于任何随机模数 m，β=b2kmodm 的行为类似于 [0,m) 上的均匀随机分布。这使得 β≤m−bk−1 的可能性很高。因此，大多数模数 m 将满足 z<1，从而导致 q~+1≥q。

为了量化这种概率，让我们假设 bk2<m<bk 并且 β 遵循均匀分布的常见情况。在这些条件下：

Pr[β≤m−bk−1]=m−bk−1m>1−2b

为了说明这一点：

• 当 b=232 时，实现更紧密界限的概率超过 1−1231。
• 当 b=264 时，实现更紧密界限的概率超过 1−1263。

也就是说，对于实践中几乎所有的模数，更紧密的界限 q~∈[q−1,q] 成立。

这是一个直观的解释：μ (即 ⌊b2km⌋) 是 m 除以 b2k 的商，β 是余数。如果 β 非常小，那么 μ 将非常接近实际商，因此 q~ 的计算将具有较小的近似误差。我们的分析表明，只要 β 不大于 m−bk−1，计算出的 q~ 最多比 q 小 1。由于这是对 β（或 m）的一个非常宽松的要求，因此大多数模数都具有更紧密的界限。

Barrett 约简实现的实践优化

更紧密的界限可以实现更快的 Barrett 约简实现。根据传统分析，我们可能需要将 r 减去 m 两次才能得到最终结果。对于给定的模数 m，如果更紧密的界限成立，那么我们最多可以将 r 减去 m 一次。这意味着我们可以节省一次减法。

这对于恒定时间实现非常有用，因为它始终减去最大次数。例如，在 RustCrypto P-256 标量域实现中，它始终减去两次。

pub(super) const fn barrett_reduce(lo: U256, hi: U256) -> U256 {
    [...]

    let r1 = [a0, a1, a2, a3, a4];
    let r2 = q3_times_n_keep_five(&q3);
    let r = sub_inner_five(r1, r2);

    // Result is in range (0, 3*n - 1),
    // and 90% of the time, no subtraction will be needed.
    let r = subtract_n_if_necessary(r);
    let r = subtract_n_if_necessary(r);
    U256::new([r[0], r[1], r[2], r[3]])
}

由于 P-256 标量域满足 β≤m−bk−1，因此更紧密的界限 q~∈[q−1,q] 成立。这意味着计算出的 q~ 最多比实际商 q 小 1。这意味着可以最多减去一次 r 才能得到最终结果。上面代码中的第二次 subtract_n_if_necessary 调用是不必要的，可以安全地删除。

基准测试表明，简单地删除第二次减法可将乘法和求逆性能提高 14%。

scalar operations/mul
    time:   [38.900 ns 38.957 ns 39.026 ns]
    change: [-14.379% -14.052% -13.734%] (p = 0.00 < 0.05)
    Performance has improved.
scalar operations/invert
    time:   [20.716 µs 20.758 µs 20.823 µs]
    change: [-14.817% -14.331% -13.969%] (p = 0.00 < 0.05)
    Performance has improved.

正如前一节所分析的，更紧密的界限适用于几乎所有的模数。因此，这种优化适用于大多数具有固定模数的 Barrett 约简（例如，ECC，ZKP）。

这是一个 Python 脚本，用于测试模数 m 是否具有更紧密的界限：

## Barret 约简的更严格的界限标准
def tighter_bound_criterion(m):
    def inner_test(m, b):
        # k 选择为满足 b^{k-1} < m < b^k
        k = 1
        while b**k < m:
            k += 1
        print("k = ", k)
        beta = b**(2*k) % m

        # 计算标准
        return beta <= m - b**(k-1)

    # 测试 b=2^32 和 b=2^64
    return inner_test(m, 2**32) and inner_test(m, 2**64)

## P-256 标量域
assert(tighter_bound_criterion(0xffffffff00000000ffffffffffffffffbce6faada7179e84f3b9cac2fc632551) == True)

## P-256 基域
assert(tighter_bound_criterion(0xffffffff00000001000000000000000000000000ffffffffffffffffffffffff) == True)

结论

我们的分析表明，对于实践中使用的大多数模数，商近似值 q~ 的误差界限可以从 [q−2,q] 收紧到 [q−1,q]。这种更紧密的界限消除了大多数情况下第二次减法的需求，从而可以实现更快，更有效的实现。

我们展示了这种优化如何应用于现实世界的密码库，例如 RustCrypto 的 P-256 标量域实现，其中删除不必要的减法可显着提高性能。这些发现广泛适用于依赖固定模数的其他密码系统和零知识证明框架。

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～