zkSNARK Groth16 协议的底层原理（第一部分）

cryptofairy
发布于 2023-09-25 16:59
阅读 1736

本文详细介绍了零知识证明（ZKP）及其在区块链中的应用，特别是zkSNARK协议的原理和实现。文章通过代码示例和图示，讲解了证明者和验证者的角色，以及如何将程序转化为算术电路。

# 零知识证明 (ZKP)

零知识证明（ZKP）是一个在区块链行业引起广泛关注的概念。许多人，包括我自己，曾将其视为一个神秘的“黑盒”。在本文及后续系列中，我将分享我对一种 ZKP 协议，特别是 zkSNARK [Groth16](https://eprint.iacr.org/2016/260.pdf) 的学习成果。

这一系列文章将配以可运行的代码，可在 [GitHub](https://github.com/tarassh/zkSNARK-under-the-hood/blob/main/groth16.ipynb) 上访问。

但首先，让我们明确什么是零知识证明。ZKP 是一个通常涉及两个参与方的协议：Alice和Bob。其要点是：Alice希望说服Bob她拥有一条特定信息，而不实际向他透露信息的任何细节。此外，伪造这样的证明几乎是不可能的，除非你口袋里有一台量子计算机。

为了通过一个例子进行说明，想象一下Alice需要向一个政府机构分享她银行账户存在的证据。使用 ZKP，她可以证明她拥有一个银行账户，而不透露她使用的是哪家银行或她账户里的金额。

ZKP 的另一个潜在应用是验证特定的计算过程。假设有软件可以进行法医分析测试。通过 ZKP，我们可以确保这些测试确实执行过，其结果可以被验证，并且几乎无法伪造。

![](https://img.learnblockchain.cn/2025/02/27/1owC2U7AY4u92TS3bUNfNTQ.png)

## zkSNARK

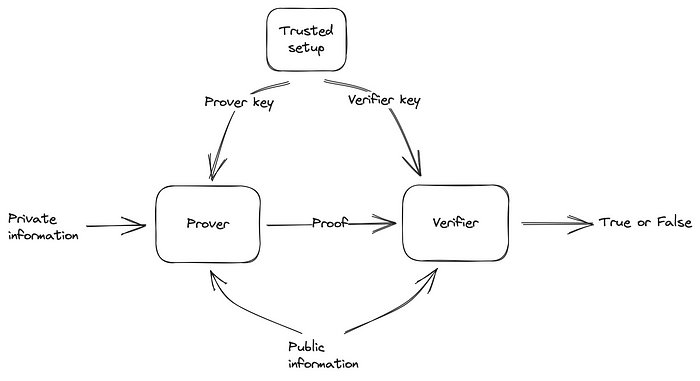
以下是描述 zkSNARK 设置的图像。与 STARK 和 Bulletproofs 等其他 ZKP 协议不同，zkSNARK 在初始化阶段需要第三方。这个第三方为证明者和验证者提供各自的密钥。

“证明者”和“验证者”模块是驻留在证明者（Alice）和验证者（Bob）一侧的程序。SNARK Groth16 协议的一个酷点是，验证者可以集成到部署在以太坊区块链上的智能合约中。这为平台引入了一组新的应用程序，并简化了区块链技术在日常生活中的采用。

让我们从证明者开始。

## 证明者

正如我之前提到的，证明者和验证者都是程序，分别由不同的参与方运行和托管。在计算要求和代码复杂性方面，证明者无疑是两者中更复杂的。因此，证明者一侧的执行时间往往会更长。

证明者的执行时间在很大程度上依赖于程序的复杂性，呈线性增长，复杂性为 O(n)。相比之下，验证者的代码复杂性保持不变，为 O(1)，确保无论证明者试图证明什么，验证时间均保持稳定。

你可能见过下面的图表，描述了证明生成的步骤。我将提供前两步的概述而不深入，而后续的步骤将通过代码例子和解释进行阐述。

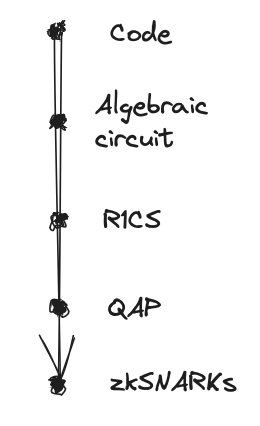
![](https://img.learnblockchain.cn/2025/02/27/1PkCgCVADHjU6iv9jJMhI1A.png)

## 代码

由于 ZKP 存在于密码学域中，因此表明了可以使用 ZKP 协议实现的程序集的限制。让我们考虑一个例子，其中证明者需要运行以下程序：

```
def compute(x, y):
    a = 5*x**3 + x**2
    b = 4*x**2*y**2 + 13*x*y**2 - 10*y
    if y == 0:
        return a
    else:
        return a + b
```

一般来说，这个函数似乎并没有特别的意义，但对于我们的目的来说，它是足够的。如你所见，该函数包含一个“if”语句。这应该暗示代码可能包含其他编程构造，例如循环。然而，在 SNARK 的情况下，计算必须是有界的。这意味着迭代次数必须提前已知，同时参数的数量以及它们的大小也应事先规定。

如果你在质疑 zkSNARK 可处理的任务范围和复杂性，这里有一小段我几年前写的代码：[https://gist.github.com/tarassh/cb2a48966fa5db3c803cba134d00b0e4](https://gist.github.com/tarassh/cb2a48966fa5db3c803cba134d00b0e4)。这是一个用于计算 h264 视频编码器的 SSIM 量度的改编版本。

回到我们的例子：正如之前提到的，ZKP 在密码学的领域内运作，因此，在数学领域也如此。因此，此代码必须转换为算术方程。有几个库能够执行此转换，包括：

- [Zokrates](https://github.com/Zokrates/ZoKrates)：该代码是用类似 Python 的语言编写的。
- [Circom](https://github.com/iden3/circom)：使用其自己的领域特定语言。
- [Pequin](https://github.com/pepper-project/pequin) 来自 Pepper-Project：这使用 C 类似的语言，与上述提供的 gist 相似。

绕过代码如何转换成方程的细节，之前提供的例子可以表示为以下方程：

```
out = 5*x**3 - 4*x**2*y**2 + 13*x*y**2 + x**2 - 10*y
```

或者：

![](https://img.learnblockchain.cn/2025/02/27/1odsvqA-VCuGHHRFG6RDHZg.png)

计算的复杂性越高，所得到的方程的长度也会越长。这个方程最终构成了构建代数电路的基础。

## 代数电路

现在，我们需要将我们的方程分解为更小的顺序操作，遵循以下规则：

- 每个操作必须由两个输入参数和一个输出参数组成。
- 只有变量（如我们的 x 和 y）可以作为输入参数。常量必须与其中一个输入参数相关联。
- 多个加法操作可以合并为一个变量。此外，减法可以表示为加法：_a_ − _b_ 相当于 _a_ +(− _b_)。

![](https://img.learnblockchain.cn/2025/02/27/1p16rKlJRziMckSiPWe5-SA.png)

所以我们的方程可以被拆分为 5 个约束。以下是所发生步骤的列表：

首先，我们可以用一个新变量 _v_ 1 替换 _x²_，并接受两个输入参数：x 和 x。现在方程将看起来像这样：

![](https://img.learnblockchain.cn/2025/02/27/1TK7mdEBgn_DJeMCaNLXvvw.png)

接下来，我们可以用一个新变量 _v_ 2 替换 _y²_，方程将如下所示：

![](https://img.learnblockchain.cn/2025/02/27/1ptXM9Vu3o1I9X6NQRIHdJA.png)

依此类推……值得注意的是，如果你选择一对不同的输入参数，比如 _v_ 1= _xy_，你将引入两个额外的约束。主要目标是识别出最少的约束，能准确表示这个方程。

![](https://img.learnblockchain.cn/2025/02/27/1x3BJS5DA5i1sJ6MpHjicgA.png)

从图示上看，这可以被视作一个电路。需要注意的是，加法操作可以合并，如公式 out=1×( _v_ 3+ _v_ 1−10 _y_ − _v_ 4+ _v_ 5) 中所示，其中 _v_ 5=13 _xv_ 2 是一个新变量。然而，为了优化以及在下篇文章中解释的原因，公式需要采取如下形式：

![](https://img.learnblockchain.cn/2025/02/27/13EiHGKKMciYKJc4DzFjdlQ.png)

## 第二部分：

[**zkSNARK Groth16 协议的底层机制（第二部分）** \\
\\
**在上一篇文章中，我们简要介绍了 SNARK 协议的前两个组成部分：代码和代数……**\\
\\
medium.com](https://medium.com/@cryptofairy/under-the-hood-of-zksnark-groth16-protocol-part-2-ca3962c50947?source=post_page-----2843b0d1558b---------------------------------------)

### 参考文献：

1. [https://www.rareskills.io/post/rank-1-constraint-system](https://learnblockchain.cn/article/11313)
2. [https://eprint.iacr.org/2016/260.pdf](https://eprint.iacr.org/2016/260.pdf)
3. [https://github.com/tarassh/zkSNARK-under-the-hood/blob/main/groth16.ipynb](https://github.com/tarassh/zkSNARK-under-the-hood/blob/main/groth16.ipynb)

>- 原文链接： [medium.com/coinmonks/und...](https://medium.com/coinmonks/under-the-hood-of-zksnark-groth16-protocol-2843b0d1558b)
>- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～

零知识证明 (ZKP)

零知识证明（ZKP）是一个在区块链行业引起广泛关注的概念。许多人，包括我自己，曾将其视为一个神秘的“黑盒”。在本文及后续系列中，我将分享我对一种 ZKP 协议，特别是 zkSNARK Groth16 的学习成果。

这一系列文章将配以可运行的代码，可在 GitHub 上访问。

zkSNARK

让我们从证明者开始。

证明者

你可能见过下面的图表，描述了证明生成的步骤。我将提供前两步的概述而不深入，而后续的步骤将通过代码例子和解释进行阐述。

代码

由于 ZKP 存在于密码学域中，因此表明了可以使用 ZKP 协议实现的程序集的限制。让我们考虑一个例子，其中证明者需要运行以下程序：

def compute(x, y):
    a = 5*x**3 + x**2
    b = 4*x**2*y**2 + 13*x*y**2 - 10*y
    if y == 0:
        return a
    else:
        return a + b

如果你在质疑 zkSNARK 可处理的任务范围和复杂性，这里有一小段我几年前写的代码：https://gist.github.com/tarassh/cb2a48966fa5db3c803cba134d00b0e4。这是一个用于计算 h264 视频编码器的 SSIM 量度的改编版本。

Zokrates：该代码是用类似 Python 的语言编写的。
Circom：使用其自己的领域特定语言。
Pequin 来自 Pepper-Project：这使用 C 类似的语言，与上述提供的 gist 相似。

绕过代码如何转换成方程的细节，之前提供的例子可以表示为以下方程：

out = 5*x**3 - 4*x**2*y**2 + 13*x*y**2 + x**2 - 10*y

或者：

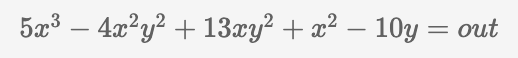
计算的复杂性越高，所得到的方程的长度也会越长。这个方程最终构成了构建代数电路的基础。

代数电路

现在，我们需要将我们的方程分解为更小的顺序操作，遵循以下规则：

每个操作必须由两个输入参数和一个输出参数组成。
只有变量（如我们的 x 和 y）可以作为输入参数。常量必须与其中一个输入参数相关联。
多个加法操作可以合并为一个变量。此外，减法可以表示为加法：a − b 相当于 a +(− b)。

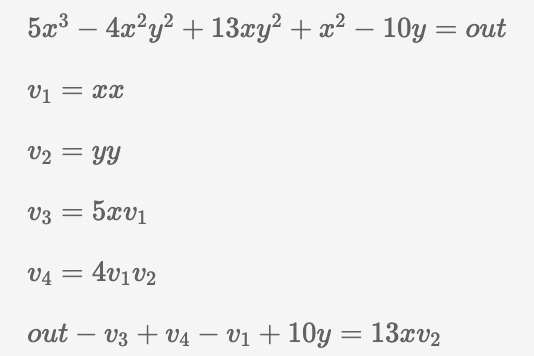
所以我们的方程可以被拆分为 5 个约束。以下是所发生步骤的列表：

首先，我们可以用一个新变量 v 1 替换 x²，并接受两个输入参数：x 和 x。现在方程将看起来像这样：

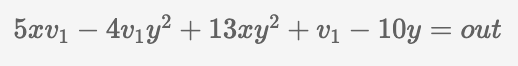
接下来，我们可以用一个新变量 v 2 替换 y²，方程将如下所示：

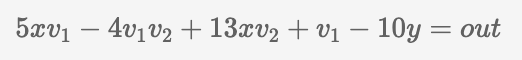
依此类推……值得注意的是，如果你选择一对不同的输入参数，比如 v 1= xy，你将引入两个额外的约束。主要目标是识别出最少的约束，能准确表示这个方程。

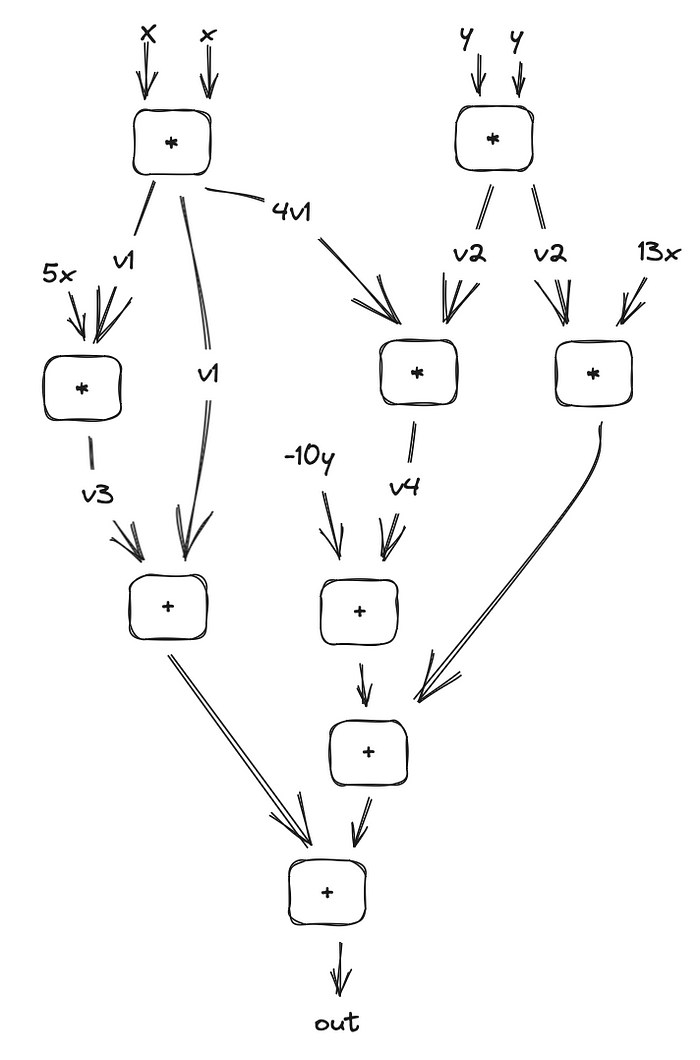
从图示上看，这可以被视作一个电路。需要注意的是，加法操作可以合并，如公式 out=1×( v 3+ v 1−10 y − v 4+ v 5) 中所示，其中 v 5=13 xv 2 是一个新变量。然而，为了优化以及在下篇文章中解释的原因，公式需要采取如下形式：

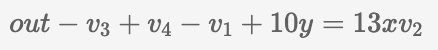
第二部分：

zkSNARK Groth16 协议的底层机制（第二部分） \ \ 在上一篇文章中，我们简要介绍了 SNARK 协议的前两个组成部分：代码和代数……\ \ medium.com

参考文献：

原文链接： medium.com/coinmonks/und...

登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～

本文参与登链社区写作激励计划，好文好收益，欢迎正在阅读的你也加入。