电力永续合约
- Paradigm
- 发布于 2021-08-18 12:26
- 阅读 119
本文介绍了一种新型衍生品——power perpetual，其价格特性与ETH及其价格的幂相关，提供了类似期权的市场流动性。文中详细讨论了该工具的机制、定价和不同实例，包括ETH^2和ETH^3 power perp，并提供Python实现示例。通过这些分析，作者希望展示power perpetual的潜力和应用前景。
大纲
引言
本文介绍了一种新的衍生品类型，power perpetual。
如果 ETH 的价格翻倍，ETH^2 power perp 将 4 倍，ETH^3 power perp 将 8 倍，ETH^5 power perp 将 32 倍。
当然，这种不对称的上升潜力并不是免费的。做多 power perpetual 的人必须定期向做空它的人支付 premium yield。
Power perpetual 提供类似全球期权的敞口，而无需行权价或到期日，因此它们有潜力将大多数期权市场的流动性集中到一个单一工具中。
在许多方面，Power perpetual 是 Everlasting Options 的逻辑下一步，且我们所知至少另有两位研究人员 Wayne Nilsen 和 llllvvuu 独立发现了它们。
机制
前提条件
Power perpetual 是在 Everlasting Options 论文中引入的永续衍生品类别的特定家族。
在本文的其余部分，我们将假设读者对 Everlasting Options 和 perpetual futures 的基本机制有所了解。
定义
Power perpetual 是一种持有针对某个基础工具价格的幂的永续衍生品。在本文中，我们假设这个基础工具是 Ether。
对于任意幂 p，ETHp power perpetual 通过每天（或其他定期的方式）支付的资金费用保持一致。如果在资金支付时，Power Perpetual 的当前价格是 $MARK，那么做多 Power Perpetual 的人可能会支付给做空者 $(MARK-INDEX) = $(MARK-ETHp)。
在 Power perpetual 的背景下，我们称这个资金费用为 premium yield，以反映这笔费用通常表示从多头支付给空头的溢价，以换取类似期权的敞口。
示例
考虑 ETH^2 power perpetual。
假设为了简单起见，ETH 的交易价为 $3，而此时 ETH^2 power perpetual 的交易价为 $9.09。那么多头需要向空头支付 $(MARK-INDEX) = $(MARK-ETH^2) = $(9.09 - 3^2) = $9.09 - $9.00 = $0.09 每个合约。
定价
概述
幂大于 1 的 Power perpetual 具有正的 convexity，这意味着持有者在价格有利时赚钱更快，而在价格不利时赔钱更慢。从期权的术语来看，我们会说它们具有正的 gamma。
就像期权通常以高于其 内在价值 的价格交易，ETH^p perp 通常以高于 ETH 的 _p_ 次幂的价格交易。
推导
遵循 Everlasting Options 论文 中的方法论，我们可以首先定价一个即将到期的幂衍生品，然后定价一组等价于所需永续的衍生品组合。
我们将在下面使用 Black-Scholes 假设来推导我们的价格。这些假设当然不是最合适的，但应作为市场做市商如何进行 power perpetual 估值的示例。
在 Black-Scholes 的假设下，定价一个即将到期的幂衍生品比定价一个期权简单得多。好奇的人可以在 StackExchange 上找到快速推导 这里。价格为
$$ S^{p} e^{t \frac{p-1}{2}(2r+pv^2)} $$
其中 S 是现货价格，p 是幂，t 是到期时间，r 是漂移或无风险利率，v 是年化波动率。
将其与 Everlasting Options PDF 的附录 B 中找到的定价方法结合，并对结果几何级数求和，我们获得了一个惟一的表达式，用于一段资金期间（假设序列收敛）的 power perpetual 的价格：
$$ S^{p} \frac{1}{2e^{-f \frac{p-1}{2}(2r+pv^2)}-1} $$
这可以被解释为指数，
$$ S^{p} $$
，乘以一个调整因子，
$$ \frac{1}{2e^{-f \frac{p-1}{2}(2r+pv^2)}-1} $$
它解释了 power perpetual 中的嵌入的选择权。注意，随着资金期的接近 0，这个调整因子接近 1。
premium yield（我们对资金利率的新术语）可以计算为
$$ \text{MARK}-\text{INDEX} = S^{p} \left( \frac{1}{2e^{-f \frac{p-1}{2}(2r+pv^2)}-1}-1 \right) $$
收敛性
与股票 Everlasting Options 不同的是，我们总是可以对其进行定价，但不良格式化的 power perpetual 可能会出现价格不收敛的情况。特别地，我们只能在满足以下条件时对 power perpetual 进行定价：
$$ \frac{e^{f \frac{p-1}{2}(2r+pv^2)}}{2} < 1 $$
直观地说，幂和波动性越高，到期较长的逐步到期的幂期货的价值越高，并且资金期越长，power perpetual 的价值就越大集中在长期到期的幂期货中。对于某些组合，等价组合的价值可能会变得无限。
通过选择一个足够小的资金期，这个问题在实践中可以很容易避免。
示例
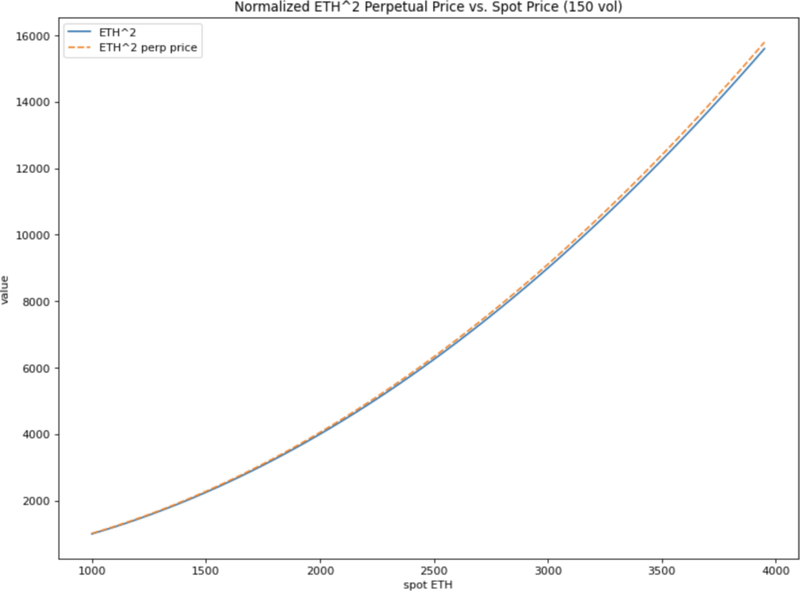
ETH^2 Power Perp
查看： https://github.com/para-dave/powerperps/blob/master/power\_perp\_prices.ipynb
ETH^2 power perp 的价格为
$$ S^{2} \frac{1}{2e^{-f(r+v^2)}-1} $$
在 Black-Scholes 假设下。
在其他条件相等的情况下，它将是 ETH 的 16 倍。
它具有恒定的 gamma 值 $$ \frac{2}{2e^{-f(r+v^2)}-1} $$，这意味着它无论 ETH 的价格如何，都提供恒定的选择权。
我们亲切地称它为 "squeeth"，是 "squared ETH" 的缩写。
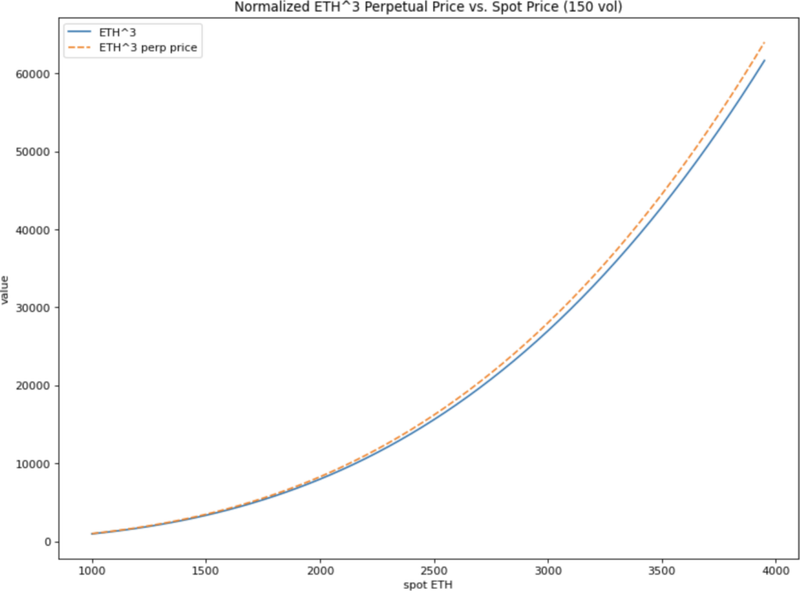
ETH^3 Power Perp
查看： https://github.com/para-dave/powerperps/blob/master/power\_perp\_prices.ipynb
ETH^3 power perp 的价格为
$$ S^{3} \frac{1}{2e^{-f(2r+pv^2)}-1} $$
在其他条件相同的情况下，它将是 ETH 的 64 倍。
你可以清楚地从图表中看到 power perp 因为其提供给持有者的选择性而以高于其指数 ETH^3 的价格交易。
Python 定价实现
你可以在 https://github.com/para-dave/powerperps/ 查看 power perpetual 定价的 Python 实现，包括在 这里 实证演示正确性的测试。
结论
Power perpetual 仍处于起步阶段，但我们自其 开始 以来一直在深入研究它们，并对其潜力感到非常兴奋。
如果你和我们一样对这个新原始工具感到好奇，请告诉我们。你可以发送电子邮件至 dave@paradigm.xyz，或在 Twitter 上 给我发消息，或联系 Opyn 的 squeeth@opyn.co。
_致谢: llllvvuu, Wayne Nilsen, Wade Prospere, Grug, Lily Francus, Dr. Benn Eifert, Jeff Wang, Mewny_
- 原文链接： paradigm.xyz/2021/08/pow...
- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
