区块链中的数学-SM2算法的推荐参数和加解密过程
- blocksight
- 更新于 2020-08-12 10:17
- 阅读 6825
本节讲了SM2算法的推荐参数和加解密过程， 可以看出加密过程跟secp256k1不同点
写在前面
最近又有不少新关注的朋友，建议从前往后阅读，学习曲线相对平滑。大牛除外 ！ 上一节讲了secp256k1公钥恢复实现,从本节起介绍下我们国家推出的国密标准算法：sm2. 国内从事区块链研发的项目出于合规的要求，尤其是联盟链项目，多数会采用国密标准。国内标准是一套体系，不仅包括加密算法，还有摘要算法，密钥交换等。由于前面讲了椭圆曲线的原理和secp256k1实例， 现在来看SM2算法就比较容易了。
SM2概述
SM2是国家密码管理局于2010年12月17日发布的椭圆曲线公钥密码算法。SM2算法是一种更先进安全的算法，在我们国家商用密码体系中被用来替换RSA算法。 随着密码技术和计算机技术的发展，目前常用的1024位RSA算法面临严重的安全威胁，这一点在RSA安全性文章中说过。我们国家密码管理部门经过研究，决定采用SM2椭圆曲线算法替换RSA算法。
SM2椭圆曲线方程：$y^2 \equiv x^3 + as + b \ mod \ p$
下面是具体推荐参数信息： 素数p： FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
系数a：FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
系数b： 28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
基点G=G（x,y）,其阶为n。
坐标Gx：32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
坐标Gy：BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0
阶n ：FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
h: 1
这个角度，可以看到与secp256k1的区别是，使用的参数不同（secp256k1参数），但方程式一致。
SM2加密过程
加密过程： 符号设定： 设消息为比特串M ，klen 为 M 的比特长度, $P_B$ 接收者公钥
作为加密者的用户 A 应实现以下运算步骤：
- 用随机数发生器产生随机数 $K \in [1,n-1]$；
- 计算椭圆曲线点 $C_1=[k]G=(x_1,y_1)$，（[k]G 表示 k*G ）;
- 计算椭圆曲线点 $S=[h] * P_B$ ，若S是无穷远点，则回到步骤1 ;
- 计算椭圆曲线点 $[k] * P_B =(x_2,y_2)$ ;
- 计算 $t=KDF(x_2 |y_2,klen)$，|表示连接，若 t 为全0比特串，则返回 步骤1；
- 计算 $C_2=M \bigoplus t$ ;
- 计算 $C_3=Hash(x_2|M|y_2)$；
- 输出密文 $C=C_1|C_2|C_3$，也可表示成 $C=(C_1,C_2,C_3)$
注意步骤3中h=1，所以也可以省略。3中的结果检查可以和2一起做。流程图表示如下：
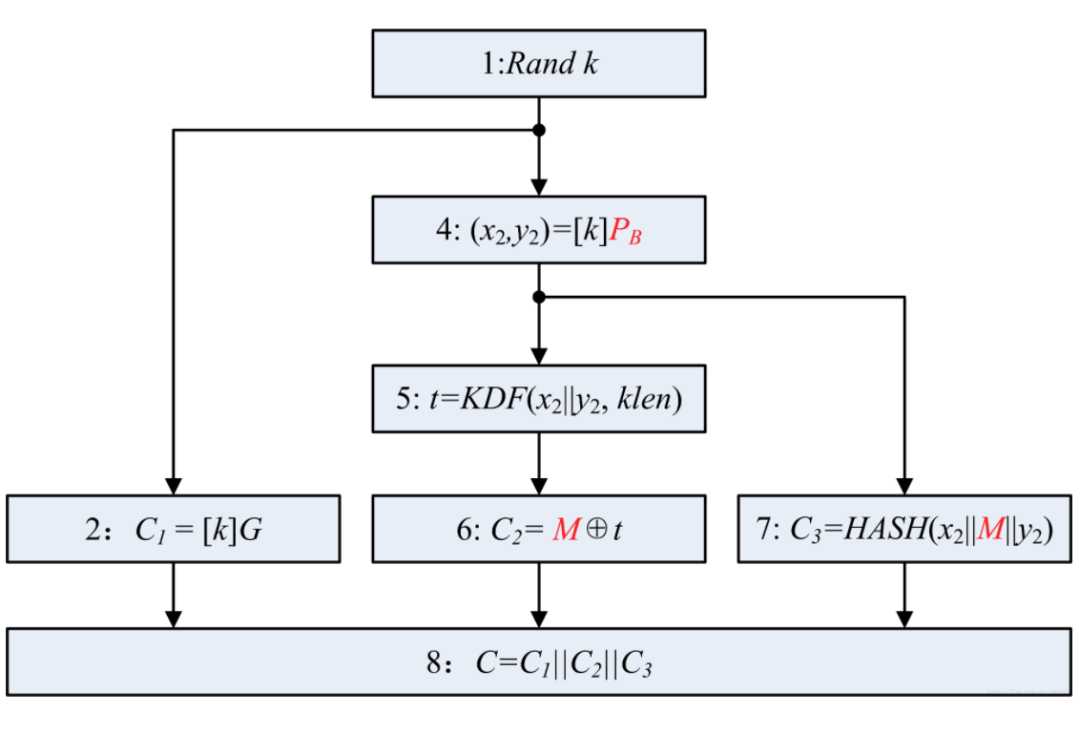
图中省略步骤3.
解密过程
解密者用户B对密文C做如下运算步骤：设klen为密文中 $C_2$ 的比特长度
-
从C中取出 $C_1$，将$C_1$转换为椭圆曲线上的点，验证$C_1$是否满足椭圆曲线方程，
-
计算 $S=[h]C_1$ ，如果S是无穷远点，出错退出；
-
计算椭圆曲线点 $d_B C_1 =(x_2,y_2)$ （h=1,可以直接这么写，严格来说是 $d_B S =(x_2,y_2)$)；
-
计算 $t=KDF(x_2|y_2,klen)$，若t为全0比特串，则报错并退出；
-
从C中取出比特串 $C_2$，计算 $M'=C_2 \bigoplus t$；
-
计算 $u=Hash(x_2|M'|y_2)$，从C中取出比特串$C_3$，若 $u !=C_3$ ，则报错退出；
-
得到明文M′。
流程图如下：
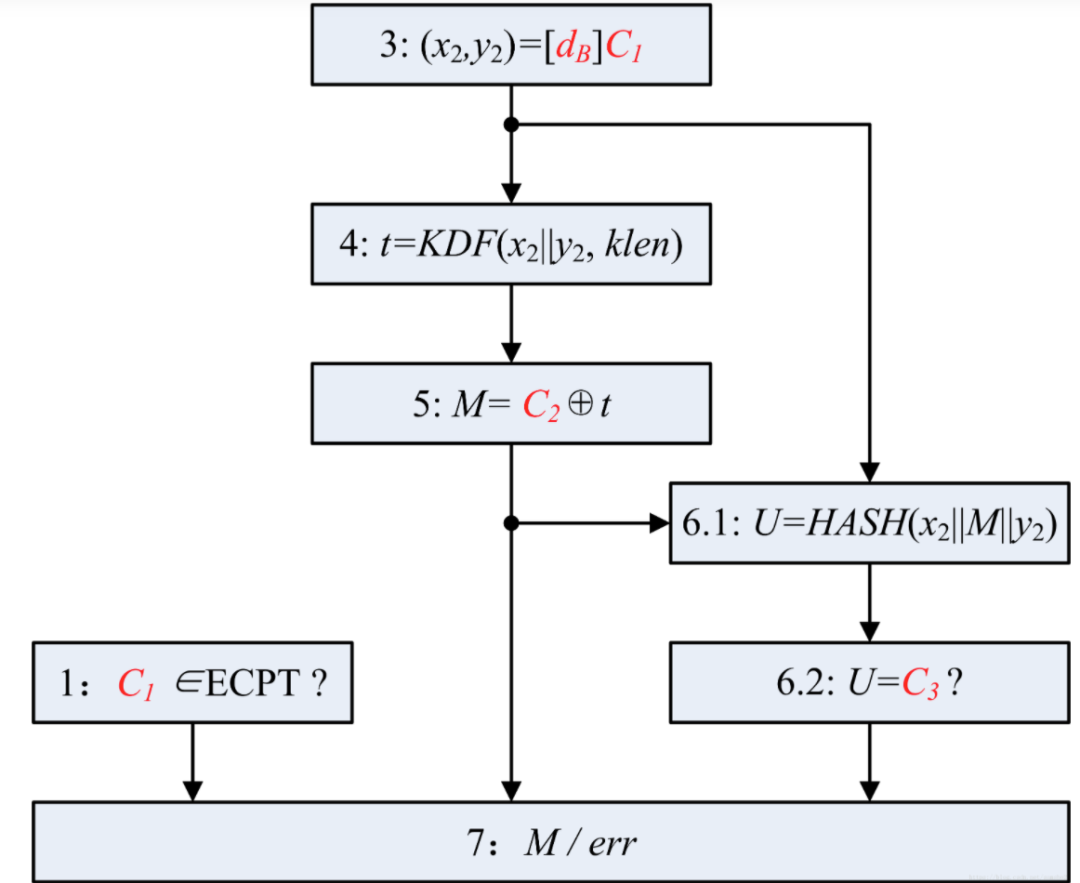
为什么这样解密可得到原文？
解密正确性
用户A持有B 的公钥 $P_B=d_B *G$，用户 B 持有私钥$d_B$ 关键是证明解密第二步得到的$(x_2,y_2)$等于加密过程步骤4 ， 这样后面算出来的t也相等，进而 $M'=C_2 \bigoplus t =M \bigoplus t \bigoplus t=M$ 那么 $(x_2,y_2)$是否相等呢？
$(x_2,y_2) =d_B C_1$ ，而 $C_1=kG $，则可以推导：
$d_B C_1=d_B kG=kP_B$
还有，显然$u==C_3$ 。
小结
本节讲了SM2算法的推荐参数和加解密过程， 可以看出加密过程跟secp256k1不同点。这个过程中用到了KDF(key derive function)下次再说。
下一篇继续说SM2的签名过程。
欢迎关注公众号：blocksight
