区块链中的数学- uniswap 中添加移除流动性的影响及算法
- blocksight
- 发布于 2020-09-26 14:25
- 阅读 13128
本文详细地解释了添加、移除流动性对unsiwap状态机状态的变化和具体的算法。
写在前面
上一节说了Uniwap核心算法中的交易价格, 这一节继续说Uniwap做市商算法之流动性改变。
本文的基础是上两篇,建议认真理解,否则理解本篇有一定难度。
百尺之台起于累土,合抱之木生于毫末,不要怕麻烦!!
下面我们详细说说流动性计算!
流动性基本介绍
uniswap流动性是指交易pool池中的代币,由流动性提供者存入到池中,我们之前说的的价格变化就是基于流动性数量来计算的。
流动性提供者可以随时增加或者删除流动性,也就是存入token对和取走token对,在取走token对的同时,取回交易手续费所积累的按比率分配的份额,也就是所谓的”流动性挖矿“收益。
添加流动性
以太坊是一个状态机模型(当然,其他区块链也都能看做状态机模型),uniswap本身也可以使用状态机来理解。
Uniswap用一个三元组(e, t, l)来代表交易平台的状态,其中e代表ETH的数量,t代表其他Token的数量,l代表当前流动性总量。添加流动性导致的状态转移方程如下:
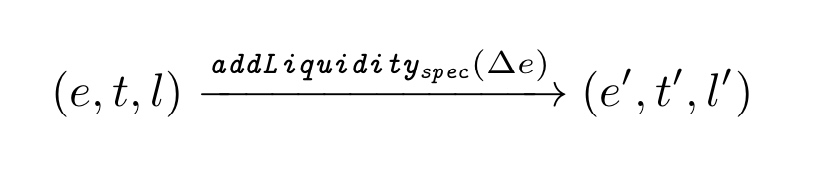
其中
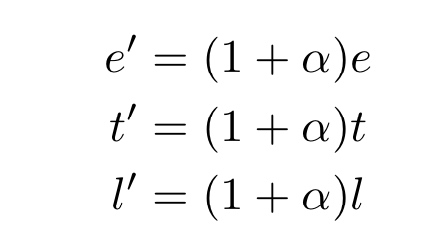
$\alpha =\Delta e/e$ , 流动性提供者即投资者可以存入 ∆e数量的 ETH 和 ∆t = t′ − t 的其他token,来挖取∆l = l′ − l 流动性。
这里e : t : l 比例是不变的,但是k = e × t是会增长的, 这一点在之前有所提及。
令 k' = e′ × t′, 则可以得到:
-
e : t : l = e′ : t′ : l′
-
k < k′
-
$\frac{k'}{k}=(\frac{l'}{l})^2 $
接下来看一下具体的算法:
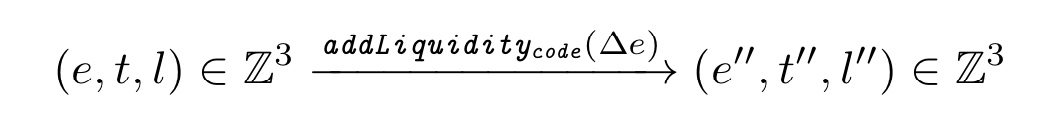
其中,
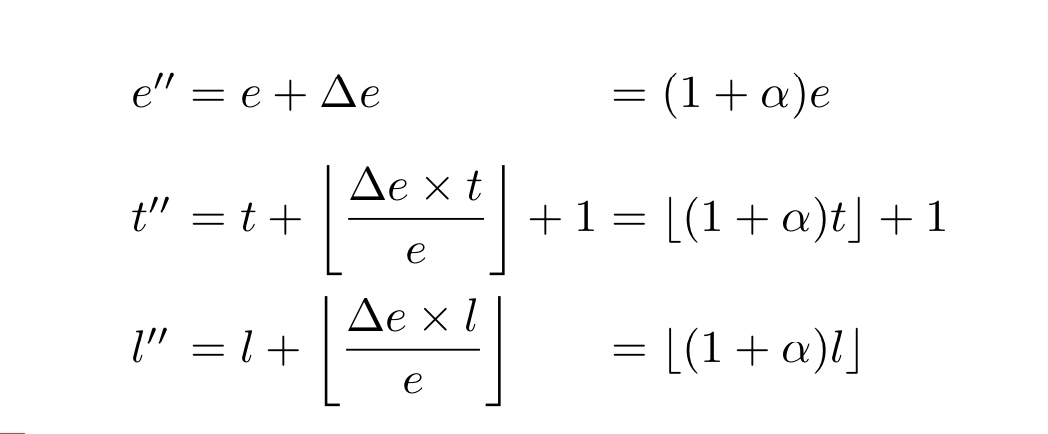
t'', l''计算中,采用了向下取整,考虑到具体计算过程中精度的因素,尤其以太坊虚机整数计算的问题。
移除流动性
流动性提供者可以收回已经存入的ETH和token,全部或者部分都可以。
状态方程如下:
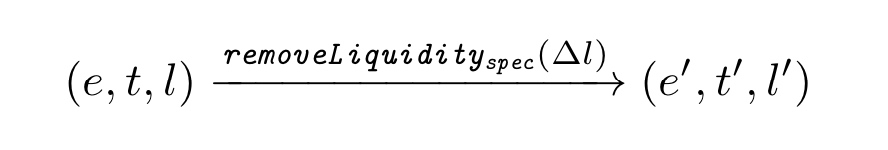
其中,
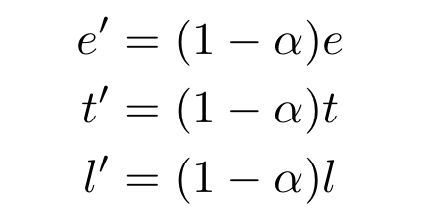
$\alpha =\Delta l/l$, 表示流动性提供者销毁∆l的流动性,得到∆e = e − e′ 个ETH和∆t = t − t′ token 对于k = e × t,k′ = e′ × t′ 可以得到:
-
e : t : l = e′ : t′ : l′
-
k > k′
-
$\frac{k'}{k}=(\frac{l'}{l})^2 $
移除流动性具体算法如下:
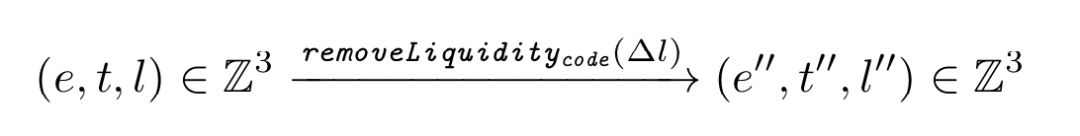
其中, t'', l''计算采用了向上取整。
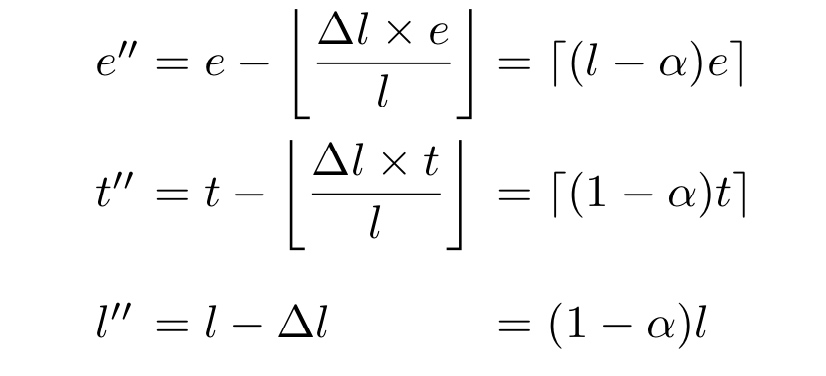
还有一点需要指出的是, 添加和移除流动性结合起来的状态变化,
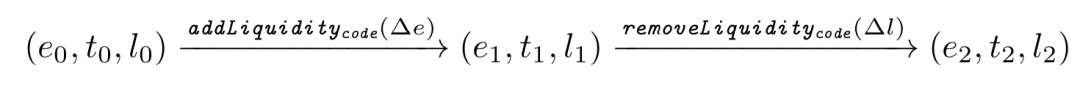
必须满足:
-
$e_0<e_2$
-
$t_0<t_2$
-
$l_0<l_2$
这样可以保证流动性提供者即投资者不能通过整数运算舍入误差获取’免费‘的收益。
小结
本文详细地解释了添加、移除流动性对unsiwap状态机状态的变化和具体的算法。总体上,简单不失优雅,
下一节继续分析uniswap中常用的方法并作为总结,结束uniswap核心算法这一系列。
欢迎关注公众号:blocksight
- 第3章:去中心化交易所 2827 浏览
- Uniswap The Compact 审计 690 浏览
- Uniswap Tribunal 审计 931 浏览
- Uniswap Labs Compact Emissary代码审计 1143 浏览
- 从零部署一套 Uniswap V2:合约、SDK、前端到上线完整实战 1045 浏览
- 探索自动化做市商协议 (AMM) 7135 浏览
- AMM 安全深度解析 - 第2部分:主流 DEX 平台深度解析 4566 浏览
- 第16章:DeFi 诉讼 1493 浏览
- 第7章:去中心化交易所(DEX) 1506 浏览
- 费用和价格预言机 648 浏览
- 协议费用 417 浏览
- 闪电贷费用 603 浏览

