区块链中的数学-椭圆曲线的背景及基本性质

写在前面

前面说过密码学是区块链的基石，没有密码学技术，区块链就是空中楼阁，也难以存在。那么密码学的基石是什么？答案是数学。

本节主要说椭圆曲线的背景及基本性质。

射影平面

首先必须要说下射影平面，因为椭圆曲线的标准方方程是定义在在射影平面上的。什么是射影平面呢？简单说来，可以理解为普通欧式平面加上无穷远点和由无穷远点组成的无穷远直线。 为什么要这样做呢？这样做达成了一个统一： 任意两条直线一定相交并且只有一个交点.

大家想想在初等几何中学到的，两条平行线是永不相交的，但是平行线永不相交只是假设，没办法严格证明。这种假设在解释一些复杂问题受到限制。于是有了无穷远点和射影平面几何。下图假想了平行线相较于无穷远点P∞

简单总结如下： 无穷远点：一条直线只有一个无穷远点，直线的两端交于无穷远点（可把直线看作封闭曲线），两条平行的直线可以看作相交在无穷远点，所有的平行直线都交于同一个无穷远点。 无穷远直线：又称理想直线.指欧氏平面上的一条假想直线，是射影平面上所有直线上的无穷远点的集合.在平面上引进无穷远直线以后，空间中每两个平面都有交线一组平行的平面相交于属于诸平行平面的一条无穷远直线。

射影平面：2维射影空间。它可以视为普通平面上追加一条无穷远点组成的无穷远直线， 它是代数几何、射影几何里最基本的对象。

射影平面坐标系

普通欧式平面下直线的方程可以表示为：

ax+by+c=0

上述方程做下改造，令x=X/Z ，y=Y/Z（Z≠0），则新方程可以表示为：

aX+bY+cZ=0;

这个方程就是新的摄影平面坐标系下的直线方程。举例说明：

点（2,3）在新的坐标体系下的坐标是多少呢？

引入Z，令X/Z=2 ，Y/Z=3（Z≠0）得到X=2Z，Y=3Z 所以新坐标为（2Z:3Z:Z），Z≠0。即（2:3:1）（4:6:2）等形如（2Z:3Z:Z）的点，可以看到单个欧式平面的点扩展成斜率相同的射影直线。

新坐标如何表示无穷远点呢？

由于无穷远点定义为平行线的交点，其中一条直线方程是：

aX+bY+c1Z =0

与之平行的直线方程是aX+bY+c2Z =0

（因为平行线斜率相同，故a,b 相同）。求两线交点，将两个方程联立，可得

c2Z= c1Z= -（aX+bY）

因为c1!=c2,所以Z=0,无穷远点表示为（X，Y，0，），普通点坐标Z！=0，无穷远直线方程Z=0. 如此新坐标系就能表示射影平面上所有点了。

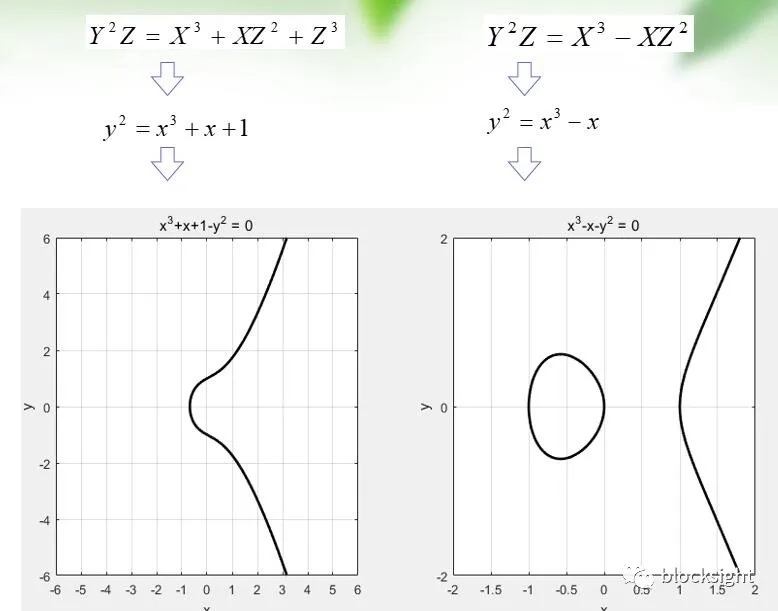
椭圆曲线方程

标准的椭圆曲线方程是在射影平面上定义的三元其次方程：

$Y^2Z+a_1XYZ+a_3YZ^2=X^3+a_2x^2Z+a_4XZ^2+a_6Z^3$

称为威尔斯特拉斯方程（Weierstrass），满足：

1.椭圆曲线方程是一个齐次方程

2.曲线上的每个点都必须是非奇异的（光滑的），偏导数FX(X,Y,Z)、FY(X,Y,Z)、FZ(X,Y,Z)不同为0

3.圆曲线的形状，并不是椭圆的。只是因为椭圆曲线的描述方程，类似于计算一个椭圆周长的方程故得名

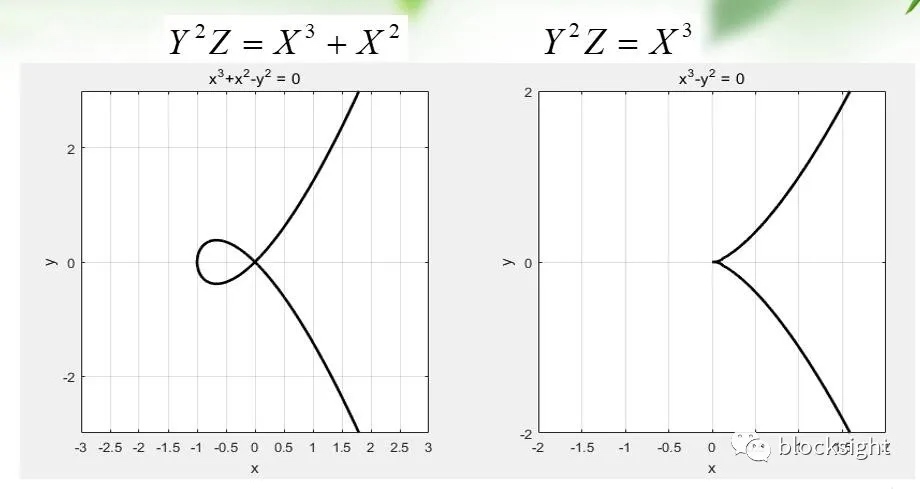
下面两个不是椭圆曲线(在零点不光滑)

椭圆曲线普通方程：

$y^2+a_1xy+a_3y=x^3+a_2x^2+a_4X+a_6$

上述标准威尔斯特拉斯方程中Z=1可得，这个一个普通欧式平面的二维曲线方程。前面说了，射影平面的上的曲线可以由普通平面的曲线加上一个无穷远点表示，椭圆曲线普通方程的无穷远点是(0, Y, 0)。

可见射影平面坐标系是向下兼容普通欧式平面坐标系的，换句话说，欧式平面坐标是射影平面坐标系的一个特例（Z=1）.

好了就到这里，下次说说椭圆曲线上点的运算。

欢迎关注公众号：blocksight