数学血脉：伦斯特拉家族

数学血统：Lenstra 家族

Apple [ here] Spotify [ here]

我知道提出这个问题很奇怪，但是哪个家族对互联网和网络安全做出了最大的贡献？嗯，Lenstra 家族完全有资格获得这个头衔。从他们的荷兰血统开始，他们为我们的现代世界做出了巨大的贡献——无论是从理论上还是从实践的角度来看。我想荷兰人的天性中存在着某种东西，他们不仅想解决实际问题，而且还想以科学的方式来解决。这种方法也是学术研究的核心——解决重大问题，并通过合作努力来解决，每个研究人员解决难题的一部分。互联网——事实上，我们的现代世界——是通过几十年来研究人员的所有惊人工作的结合而创造出来的。

会见密码学和问题解决兄弟

我的祖父是一名电工，我的父亲也是。我想电子的东西是流淌在我的血液里的。这是我职业生涯的起点，而且我一直热爱与电子相关的一切。我必须承认，小时候我给了自己太多的电击，因为拆东西的诱惑对我来说太大了。而且，我们常常只是认为电力——以及它在现代世界中的所有应用——是理所当然的，这仍然让我感到惊讶。如果没有我们对电力的控制以及一切与电有关的东西，我们会怎么样？当然，你现在也不会在读这篇文章了。

所以，有时，有些东西在我们的血液里，决定了我们未来的职业。对于 Lenstra 家族来说，情况肯定是这样的，从他们的荷兰血统来看，Hendrik、Arjen、Andries 和 Jan Karel 已经成为重要的数学家。

对于那些研究网络的人来说，这些兄弟中最著名的人之一是强大的 Jan Karel Lenstra(J.K. Lenstra)，他的许多重大突破包括调度、本地搜索和旅行商问题。因此，我们都可以感谢 Jan 在路由问题上的工作，这导致了互联网上路由协议的创建：

解决互联网上的路由问题，使得互联网能够扩展到我们现在看到的水平，并且我们可以几乎立即访问来自地球任何地方的信息。我们可以感谢 J.K. Lenstra 提供了这个基础。

Arjen 的工作重点是密码学，包括许多经典的论文，例如与多项式分解相关的论文以及一篇题为“Ron was wrong. Whit is right”[ here] 的著名论文：

但是，Arjen 被引用最多的论文包括他的兄弟（Hendrik W. Lenstra Jr.）作为合著者 [3]：

而且，在当今的 Microsoft Word 和 LaTeX 时代，难道你不喜欢纸上的笔迹标记吗？兄弟俩还合作撰写了另一篇经典论文——其中包括强大的 J.M Pollard [2]：

Lenstra–Lenstra–Lovász (LLL)

当两兄弟一起工作时，他们创造了一些最好的作品，正是经典的《有理系数多项式分解》[3] 论文促成了 Lenstra–Lenstra–Lovász (LLL) 方法 [ paper]。这篇论文还包括强大的 Laszlo Lovász [ here]（他的 h 指数为 109）：

这将使用这种方法（定义为 Lenstra–Lenstra–Lovász (LLL)）来破解签名，并发现用于对消息进行数字签名的私钥。这将搜索用于使用 ECDSA 签署消息的私钥。在这种情况下，我们将生成两个签名，然后搜索私钥。

最常见的签名之一是 ECDSA（椭圆曲线数字签名算法），它与比特币和以太坊一起使用。有了它，Bob 创建一个随机私钥 (priv)，然后从以下位置创建一个公钥：

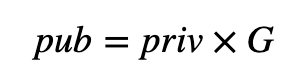
接下来，为了创建消息 M 的签名，他创建一个随机数 (k) 并生成签名：

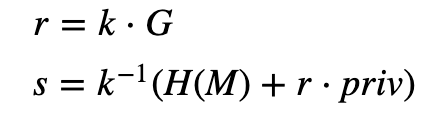
然后签名是 (r, s)，其中 r 是点 kG 的 x 坐标。H( M) 是消息 (M) 的 SHA-256 哈希，并转换为整数值。如果任何签名的 k 值被泄露，入侵者可以使用以下方法确定私钥：

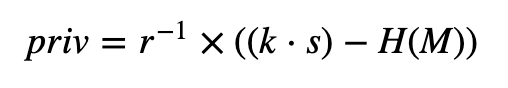
其原理如下：

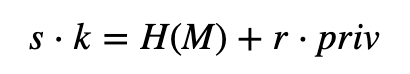
所以：

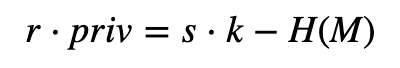
对于 priv：

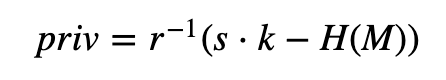
然后，我们可以使用代码 [ here] 来实现基于 LLL 的搜索方法：

import ecdsa
import random
import libnum
import olll
import hashlib
import sys# https://blog.trailofbits.com/2020/06/11/ecdsa-handle-with-care/

G = ecdsa.NIST256p.generator
order = G.order()print ("Curve detail") # 曲线细节
print (G.curve())
print ("Order:",order) # 阶
print ("Gx:",G.x())
print ("Gy:",G.y())
priv = random.randrange(1,order)

Public_key = ecdsa.ecdsa.Public_key(G, G * priv)
Private_key = ecdsa.ecdsa.Private_key(Public_key, priv)

k1 = random.randrange(1, pow(2,127))
k2 = random.randrange(1, pow(2,127))msg1="Hello"
msg2="Hello1"if (len(sys.argv)>1):
    msg1=(sys.argv[1])
if (len(sys.argv)>2):
    msg2=(sys.argv[2])m1 = int(hashlib.sha256(msg1.encode()).hexdigest(),base=16)
m2 = int(hashlib.sha256(msg2.encode()).hexdigest(),base=16)

sig1 = Private_key.sign(m1, k1)
sig2 = Private_key.sign(m2, k2)print ("\nMessage 1: ",msg1) # 消息 1
print ("Message 2: ",msg2) # 消息 2
print ("\nSig 1 r,s: ",sig1.r,sig1.s) # 签名 1 r,s
print ("Sig 2 r,s: ",sig2.r,sig2.s) # 签名 2 r,s
print ("\nk1: ",k1)
print ("k2: ",k2)print ("Private key: ",priv) # 私钥r1 = sig1.r
s1_inv = libnum.invmod(sig1.s, order)
r2 = sig2.r
s2_inv = libnum.invmod(sig2.s, order)

matrix = [[order, 0, 0, 0], [0, order, 0, 0],\
[r1*s1_inv, r2*s2_inv, (2**128) / order, 0],\
[m1*s1_inv, m2*s2_inv, 0, 2**128]]

search_matrix = olll.reduction(matrix, 0.75)
r1_inv = libnum.invmod(sig1.r, order)
s1 = sig1.s

for search_row in search_matrix:
    possible_k1 = search_row[0]
    try_private_key = (r1_inv * ((possible_k1 * s1) - m1)) % order

    if ecdsa.ecdsa.Public_key(G, G * try_private_key) == Public_key:
        print("\nThe private key has been found") # 找到了私钥
        print (try_private_key)

一个示例运行是 [ here]：

Curve detail
CurveFp(p=115792089210356248762697446949407573530086143415290314195533631308867097853951, a=-3, b=41058363725152142129326129780047268409114441015993725554835256314039467401291, h=1)
Order: 115792089210356248762697446949407573529996955224135760342422259061068512044369
Gx: 48439561293906451759052585252797914202762949526041747995844080717082404635286
Gy: 36134250956749795798585127919587881956611106672985015071877198253568414405109Message 1:  hello
Message 2:  goodbyeSig 1 r,s:  115147473306387600780958700123813228515236063210926878166205132442387398405974 78422551211706787416844282162734821752165856246967039833155909830188362436931
Sig 2 r,s:  72928835934664146344187979593177679887058837944881110039604237325952057142506 34831214671095490475430891005520988929988430486970993941519827388518136205821k1:  2238116107289725910464212774221939217
k2:  23155266189808659522258191324208917771
Private key:  3126769432554995310932591745910468237140199425344791317304188208833915624553

这是一篇非常精彩的论文，非常值得一读。

2019 年 12 月，由 INRIA 的 Paul Zimmermann 领导的一个团队宣布分解了有史以来最大的 RSA 模数 (RSA-240)：

RSA-240 = 124620366781718784065835044608106590434820374651678805754818788883289666801188210855036039570272508747509864768438458621054865537970253930571891217684318286362846948405301614416430468066875699415246993185704183030512549594371372159029236099RSA-240 = 509435952285839914555051023580843714132648382024111473186660296521821206469746700620316443478873837606252372049619334517
        × 244624208838318150567813139024002896653802092578931401452041221336558477095178155258218897735030590669041302045908071447

该因式分解涉及将一个 795 位的整数分解为其质数因子。这导致行业专家定义 RSA 只有使用至少 2,048 位密钥才是安全的。实际上，Arjen 在 1990 年代是第一个破解早期 RSA 挑战赛的人，并成功地对 330（100 位十进制数字）、364、426 和 430 位模数值进行因式分解 [ here]：

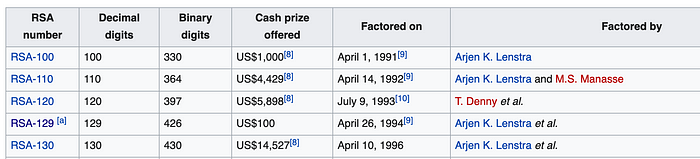
使用椭圆曲线分解

Hendrik W. Lenstra Jr. 于 1979 年成为阿姆斯特丹大学的教授，然后在 1987 年被任命为加州大学伯克利分校的教授。他最著名的博士生之一是 Daniel J. Bernstein [ here]，他以生产 Curve 25119、ChaCha20 和 Poly1305 等标准而闻名。在 Hendrik 被任命到伯克利的那一年，他概述了一种使用椭圆曲线方法分解积分的方法 [1]：

几种公钥方法的安全性依赖于分解由大质数相乘创建的模数的难度。RSA 就是一个很好的例子，我们取两个大质数（p 和 q），并将它们相乘来创建一个模数（N）。那么困难在于，如果我们知道 N，就能够找到 p 和 q。我们可以用于此因数分解的两种核心方法是通用数域筛选法 (GNFS) 和 ECM（椭圆曲线法）。

ECM

通过他的方法，我们定义了从椭圆曲线上的一个点 P 移动到 2 P。 为此，我们找到点 P 的切线，并使用它来找到 2 P。该切线将使用斜率 (s) 和 a/b 形式的梯度来定义。为此，我们必须找到 b 的模逆。如果我们找不到 b 的模逆，则 N 的一个因子是 gcd( N, b)，其中 gcd() 是最大公约数。

如果我们的曲线是 y ²= x ³+ ax + b，则斜率 (s) 将是：

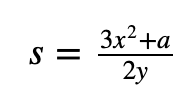
如微分中所定义。详细地说，我们首先在以下椭圆曲线上选取一个随机点 P =( x 0, y 0)：

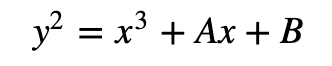
我们还选择一个随机值 A，然后计算：

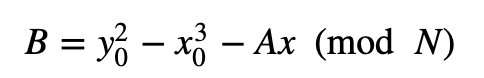
对于曲线上两个点：P =( Px, Py) 和 Q =( Qx, Qy)，它们之间线的斜率将为：

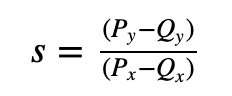
有了这个，我们就有 s 的形式为 a/b (mod N)。

接下来我们定义：

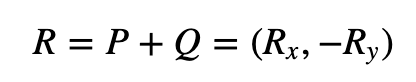
并使用：

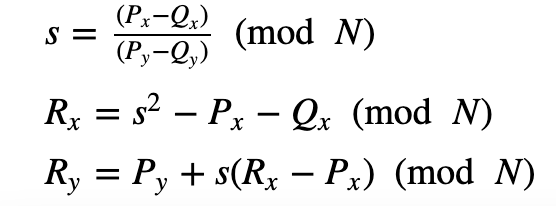
如果 Px = Qx 且 Py =− Qy，我们定义为 0 [身份]，否则我们计算 R = P + P =2 P =( Rx,− Ry)：

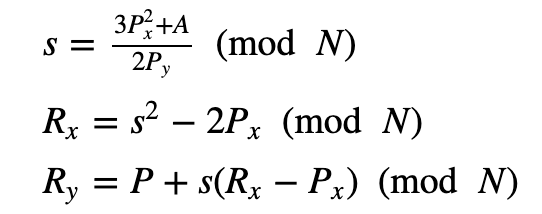
以下是一些测试运行：

• N=15（因子：3 和 5 尝试！
• N=6,161（因子：61 x 101）尝试！
• N=32,128（因子：2 x 2 x 2 x 2 x 2 x 2 x 2 x 251）尝试！
• N=53,421（因子：3 x 17,807）尝试！
• N=55,440（因子：2 x 2 x 2 x 2 x 3 x 3 x 5 x 7 x 11）尝试！
• N=999,999（因子：3 x 3 x 3 x 7 x 11 x 13 x 37）尝试！
• N=10,000,000（因子：2 x 2 x 2 x 2 x 2 x 2 x 2 x 5 x 5 x 5 x 5 x 5 x 5 x 5）尝试！
• N=100,001（因子：11 x 9091）尝试！
• N=455,839（因子：559 x 761）尝试！
• N=3,789,829（因子：3209 x 1181）尝试！
• N=7,388,399（因子：3571 x 2069）尝试！
• N=392,524,199（因子：431 x 919 x 991）尝试！

使用的代码的概要是 [ code]：

##!/usr/local/bin/python
## -*- coding: utf-8 -*-
import math
import random
import sys#y^2=x^3+ax+b mod n prime=[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271 ]
## ax+by=gcd(a,b). This function returns [gcd(a,b),x,y]. Source Wikipedia
def extended_gcd(a,b):
    x,y,lastx,lasty=0,1,1,0
    while b!=0:
        q=a/b
        a,b=b,a%b
        x,lastx=(lastx-q*x,x)
        y,lasty=(lasty-q*y,y)
    if a<0:
        return (-a,-lastx,-lasty)
    else:
        return (a,lastx,lasty)# pick first a point P=(u,v) with random non-zero coordinates u,v (mod N), then pick a random non-zero A (mod N),
## then take B = u^2 - v^3 - Ax (mod N).
## http://en.wikipedia.org/wiki/Lenstra_elliptic_curve_factorizationdef randomCurve(N):
    A,u,v=random.randrange(N),random.randrange(N),random.randrange(N)
        B=(v*v-u*u*u-A*u)%N
        return [(A,B,N),(u,v)]  # Given the curve y^2 = x^3 + ax + b over the field K (whose characteristic we assume to be neither 2 nor 3), and points
    # P = (xP, yP) and Q = (xQ, yQ) on the curve, assume first that xP != xQ. Let the slope of the line s = (yP - yQ)/(xP - xQ); since K           # is a field, s is well-defined. Then we can define R = P + Q = (xR, - yR) by
    #   s=(xP-xQ)/(yP-yQ) Mod N
    #   xR=s^2-xP-xQ    Mod N
    #   yR=yP+s(xR-xP)  Mod N
    # If xP = xQ, then there are two options: if yP = -yQ, including the case where yP = yQ = 0, then the sum is defined as 0[Identity].           # thus, the inverse of each point on the curve is found by reflecting it across the x-axis. If yP = yQ != 0, then R = P + P = 2P =         # (xR, -yR) is given by
    #   s=3xP^2+a/(2yP) Mod N
    #   xR=s^2-2xP  Mod N
    #   yR=yP+s(xR-xP)  Mod N
    #   http://en.wikipedia.org/wiki/Elliptic_curve#The_group_law''')

def addPoint(E,p_1,p_2):
    if p_1=="Identity": return [p_2,1]
    if p_2=="Identity": return [p_1,1]
    a,b,n=E
    (x_1,y_1)=p_1
    (x_2,y_2)=p_2
    x_1%=n
    y_1%=n
    x_2%=n
    y_2%=n
    if x_1 != x_2 :
        d,u,v=extended_gcd(x_1-x_2,n)
        s=((y_1-y_2)*u)%n
        x_3=(s*s-x_1-x_2)%n
        y_3=(-y_1-s*(x_3-x_1))%n
    else:
        if (y_1+y_2)%n==0:return ["Identity",1]
        else:
            d,u,v=extended_gcd(2*y_1,n)
            s=((3*x_1*x_1+a)*u)%n
            x_3=(s*s-2*x_1)%n
            y_3=(-y_1-s*(x_3-x_1))%n    return [(x_3,y_3),d]    # http://en.wikipedia.org/wiki/Elliptic_curve_point_multiplication
    #   Q=0 [Identity element]
    #   while m:
    #       if (m is odd) Q+=P
    #       P+=P
    #       m/=2
    #   return Q')def mulPoint(E,P,m):
    Ret="Identity"
    d=1
    while m!=0:
        if m%2!=0: Ret,d=addPoint(E,Ret,P)
        if d!=1 : return [Ret,d]  # as soon as i got anything otherthan 1 return
        P,d=addPoint(E,P,P)
        if d!=1 : return [Ret,d]
        m>>=1
    return [Ret,d]
def ellipticFactor(N,m,times=5):
    for i in xrange(times):
        E,P=randomCurve(N);
        Q,d=mulPoint(E,P,m)
        if d!=1 : return d
    return Nfirst=True
n=455839
if (len(sys.argv)>1):
        n=int(sys.argv[1])print n,'=',for p in prime:
    while n%p==0:
        if (first==True):
            print p,
            first=False
        else:
            print 'x',p,
        n/=pm=int(math.factorial(2000))
while n!=1:
    k=ellipticFactor(n,m)
    n/=k
    if (first==True):
        print k,
        first=False
    else:
        print 'x',k,

结论

因此，在荷兰人解决实际问题和使用科学方法方面存在着某种东西，而 Lenstra 家族也像其他任何家族一样强调了这一点。

对于整数的因式分解，过去的伟大公钥方法可能无法很好地扩展到 2020 年代，尤其是因为因式分解变得越来越强大，并且实际上正在超越摩尔定律。如果你有兴趣，这里还有其他因式分解方法：

• 平方差。Diffsq。这使用平方差方法进行分解。
• 整数因子。Factors。确定整数的因子。
• Pollard 的 ρ 方法（因式分解整数）。Pollard。Pollard ρ 方法分解整数。
• 简化 ap(mod N) Go。简化 a^p(mod N) 运算。
• 平滑数。Go。平滑数的概述。
• 二次剩余（mod p）。Go。二次剩余（mod p）的概述。
• 二次剩余（mod N），其中 N = pq。Go。二次剩余（mod N）的概述，其中 N 由两个质数组成。
• Dixon。Go。Dixon 方法。

参考文献

[1] Lenstra Jr, H. W. (1987). 使用椭圆曲线分解整数。数学年鉴，649–673。

[2] Lenstra, A. K., Lenstra, H. W., & Lovász, L. (1982). 有理系数多项式分解。数学年鉴，261(文章)，515–534。

[3] Lenstra, A. K., Lenstra, H. W., Manasse, M. S., & Pollard, J. M. (1993). 数域筛选法。在_数域筛选法的发展_中（第 11–42 页）。施普林格，柏林，海德堡。

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～