区块链中的数学-蒙哥马利曲线和应用实例Curve25519
- blocksight
- 更新于 2020-10-28 13:25
- 阅读 9738
本文介绍了蒙哥马利曲线和应用实例Curve25519，Curve25519得到广泛使用，其自身的长处简单说明，没有展开
写在前面
上一节说了扭曲爱德华曲线，扭曲爱德华曲线是EdDSA（爱德华曲线数字签名）体制的核心。
本节说下蒙哥马利曲线和Curve25519, 为什么说它呢？因为它与Ed25519签名相关联。
蒙哥马利曲线
蒙哥马利曲线（Montgomery curve）是另一种形式的椭圆曲线，方程如下：
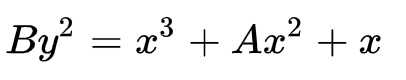
其中系数A, B ∈ 有限域K，且B($A^2$ − 4) ≠ 0.
下图是在实数域上方程 的曲线
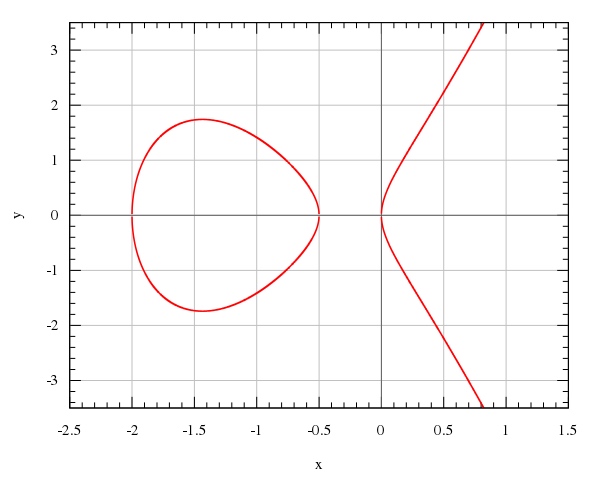
点加法规则
前面我们说了Weierstrass曲线上两点相加的几何意义，是通过两点连接一条直线，与曲线相交第三个点关于x轴的对称点就是所求的和, 蒙哥马利曲线也是这样定义两点求和算法： 已知 ）$P_1(x_1,y_1)$,$P_2(x_2,y_2)$两点和之和$P_3(x_3,y_3)$
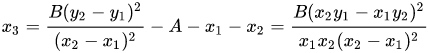
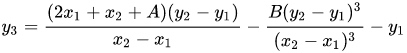
这个计算结果容易得到，令通过点$P_1$，$P_2$的直线为y = lx + m, 可得:
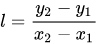
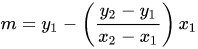
代入蒙哥马利曲线方程，
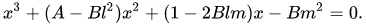
该方程有三个解$x_1$，$x_2$,$x_3$ ,$(x-x_1)(x-x_2)(x-x_3)$ = 0, 根据维达（Vieta）定理或者直接比较系数，得到：
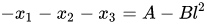
从而得到：
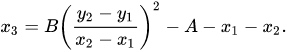
代入直线公式，即得到$y_3$坐标，注意最后是关于x轴的对称点。
如何两个点相同即2P求法稍微有些不同。主要是直线斜率计算变成了点切线问题，斜率l:
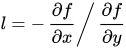
可算得
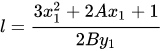
使用新斜率l代入前面$x_3,y_3$公式，可得到：
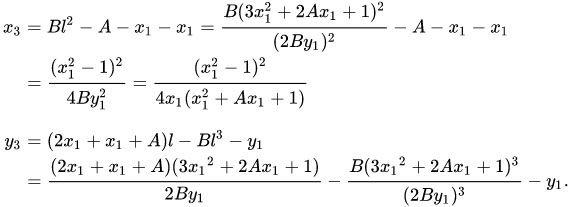
接下来说下蒙哥马利曲线广泛应用的实例Curve25519。
Curve25519
Curve25519是蒙哥马利曲线形式的一个实例， 声称是最快的Diffie-Hellman密钥交换函数，由Daniel J. Bernstein教授在2005年设计，提供128比特位安全性，并未被任何已知专利所涵盖。方程为：
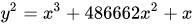
素数域$p = 2^{255}-19 $, 也是名字中25519的由来。 基点横坐标 x = 9， 群秩为$ 2^{255}+27742317777372352535851937790883648493$，
Curve25519的构造避免了许多潜在的实现方面陷阱，它不受计时攻击，能接受任何32字节字符串作为有效公钥(实际工程应用中，0除外)，并且不需要验证给定点是否属于曲线，或者是否由基点生成。
2013年斯诺登事件以后，得到大量关注和使用，目前应用已经非常广泛，包括ssh, tls,OpenSSL,Libsodium等，实际成为NIST P-256椭圆曲线算法的替代品（前者被广泛质疑有后门（back door））.
关于Curve25519，先说到这，以后有用到再说。
小结
本文介绍了蒙哥马利曲线和应用实例Curve25519，Curve25519得到广泛使用，其自身的长处简单说明，没有展开,感兴趣的话以后可以再说明，本文参考
https://eprint.iacr.org/2017/293.pdf
https://en.wikipedia.org/wiki/Curve25519
最近几篇的思路是： 爱德华曲线--> 扭曲爱德华曲线--> 蒙哥马利曲线（Curve25519）--> Ed25519签名
好了，下一篇继续介绍区块链中正在使用的Ed25519签名算法！
欢迎关注公众号：blocksight
