网络安全基石的奠基人：Ralph C Merkle

网络安全奠基人：Ralph C Merkle

我很幸运能与一些为互联网安全奠定基础的伟大人物交谈，昨天我和其中一位伟人 Ralph C Merkle 进行了交流：

密码学界的领导者：Ralph Merkle - Youtube

Ralph 是公钥密码学的共同发明人，密码散列的发明者，创建了 Merkle 的谜题，是 Merkle-Hellman 背包密码系统的共同发明人，并发明了 Merkle 树。他于 1974 年在加州大学伯克利分校获得计算机科学学士学位，并于 1979 年在斯坦福大学获得电气工程博士学位。最近，他是人体冷冻学方面的研究员和演讲者。Ralph 曾是著名的施乐 PARC（帕洛阿尔托研究中心）的研究科学家，以及 Zyvex 的纳米技术理论家。

Ralph 还曾担任佐治亚理工学院的杰出教授、IMM 的高级研究员、奇点大学的教员以及 Alcor 生命延续基金会的董事会成员。1998 年，他因纳米技术理论而共同获得费曼纳米技术奖。2010 年，他因发明公钥密码学而获得 IEEE Richard W. Hamming 奖章，并于 2011 年入选美国国家网络安全名人堂。2020 年，他因“对公钥密码学、哈希算法、Merkle 树和数字签名的发展做出根本性贡献”而获得列夫钦奖。

公钥密码学的发明

许多人认为，本科阶段不太可能产生突破性的想法，但事实并非如此。1974 年，Ralph 在课程作业定义中向他的教授提出了公钥的想法，并定义了一种密钥交换方法（称为 Merkle 的谜题）。他的教授拒绝了他的想法，直到 Ralph 听到 Martin Hellman 和 Whitfield Diffie 在斯坦福的工作后，这个想法才得以复活。下面的文字显示：

项目 2 看起来更合理，也许是因为你对项目 1 的描述非常混乱

随后，Ralph 将他的想法作为论文提交给 ACM 通讯，但由于他的论文缺乏正式的文献综述以及对其他作品的引用而被拒绝。Ralph 认为，不可能有参考文献，因为根本没有其他类似的作品。三年后，这篇论文被接受了，但这次它有对其他作品的引用。

Ralph 的想法是，Bob 给 Alice 一些谜题来解决，Alice 选择其中一个并解决它。然后 Alice 返回答案和另一个谜题。这两个谜题的答案随后用作 Bob 和 Alice 之间的秘密，因此是他们用来发送秘密消息的密钥。Eve 正在监听，她可以解决这些谜题，她必须解决 Bob 和 Alice 的谜题，如果谜题的数量很大，并且破解它们所需的时间很长，Eve 将花费更长的时间来发现共享的秘密 [示例]。

历史

好的。现在是 1978 年，你是一名 26 岁的博士生，你一直在仔细研究你的导师关于密钥交换的经典论文（Martin Hellman）。在你的导师的论文中，他提出可能存在陷门函数，我们可以创建两个密钥 - 一个用于加密，另一个用于解密。在回顾了他本科阶段的工作后，Ralph 冲进去告诉他杰出的导师，他已经找到了他导师提出的方法。世界很快就会在以下经典论文中发现这一发现：

对于 Ralph 来说，这是公钥加密的发明，它现在为互联网上的安全提供了核心。他的实际方法后来被打破了，但他展示了如何创建两个密钥的可能性：一个用于锁定，另一个用于打开。对他来说，任务是创建一个公钥，该公钥极难从相关的私钥中推导出来。

独一无二的导师和论文

Ralph 的论文于 1979 年成功答辩[此处]，他的致谢总是博士论文审核者了解博士环境的一个重要来源--暗示了当时斯坦福大学和加州大学伯克利分校在密码学方面的创意温床：

能够在如此富有创造力和激励性的环境中，在 Steve Pohlig 的帮助下，以及伟大的 Whitfield Diffie 的帮助下，然后拥有 Martin Hellman 这样的导师，一定是一种荣幸。有这样的人才在你身边，你要么会开花结果，要么会枯萎，介于两者之间的可能性很小。

难道你不喜欢“……并且在我最需要的时候鼓励了我”这句话吗？这句话暗示了 Ralph 在研究他的新方法时遇到了困难，而 Martin 在那里指导和支持他，最重要的是不妨碍他，而是一位提供建设性反馈的导师。

Ralph C. Merkle 出生于 1952 年，他的博士学位是在 1979 年在斯坦福大学获得的，题目是“保密性、身份验证和公钥系统”。许多人认为，博士阶段的想法是在博士研究中孵化的，但对于 Ralph 来说，他的第一个想法是本科阶段的作业：设计一种通过不安全信道进行通信的方案。

此后，他转向了其他领域，但他因发现公钥加密方法而获得了认可，并在 1996 年获得了 ACM 公钥密码学发明奖，并在 2000 年获得了 RSA 发明奖。随后获得了许多奖项，包括在 2011 年入选国家发明家名人堂。

对 Ralph 来说，他的方法持续了四年，之后 Adi Shamir 表明，它可以很容易地被破解：

• Shamir, Adi. “一种用于破解基本 Merkle-Hellman 密码系统的多项式时间算法。”密码学进展。Springer US，1983 年。

你一定会为在文字处理器出现之前必须为博士论文付出的努力而感到高兴，那时必须有人实际输入所有字符（并检查）：

Merkle 树

在五页简短的篇幅中，Merkle 于 1979 年 9 月提交了他的专利，并阐述了后来成为我们所知的区块链的方法[此处]：

该专利被分配给了斯坦福大学，其中概述了一种通过哈希树验证数据的方法，其中顶层哈希可用于验证块内的所有数据：

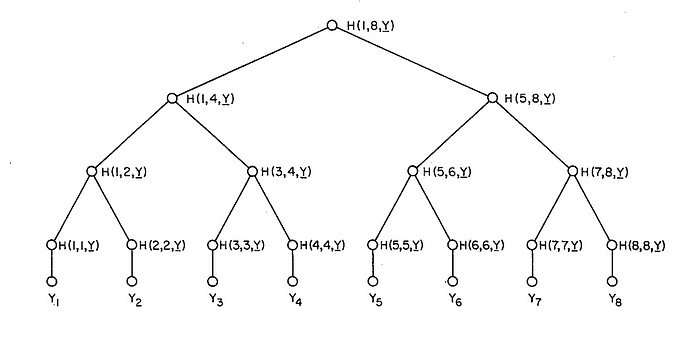
在此，数据元素 Y1 和 Y2 被哈希，然后从该哈希创建一个哈希，最终我们到达树的顶部，其中可以从顶层哈希证明所有数据的有效性，并且任何更改都可以在树中快速追踪。这是一个如此漂亮的模式，说出它是什么，它就完成了。它有四个基本声明，但基本上，它是围绕树的核心图形构建的。最美好的数学在其最精彩的形式。这有很多核心应用，其中一个是 Bob 拥有许多私钥，然后将这些密钥哈希处理成一个公钥。每当 Bob 使用他的一个私钥时，他都可以向任何人证明他知道从他的私钥到他的公钥的路径 - 从而表明“没有什么花招”。

假设我们有两家银行，每天进行数十亿笔交易，他们想检查是否所有交易或一批交易都已正确收到。一种方法是使用 Merkle 树（或哈希树），这是 Ralph Merkle 在 1979 年获得专利的一种方法[此处]，其中每个非叶节点都是其子节点的哈希。然后，要检查所有交易，我们将计算哈希值并计算根哈希，然后交换它。

假设我们有 Bob The Bank 和 Alice Online，他们交换交易。如果他们想在一天结束时检查他们的交易，他们可以通过将非叶节点与其子节点的哈希进行哈希来计算哈希树：

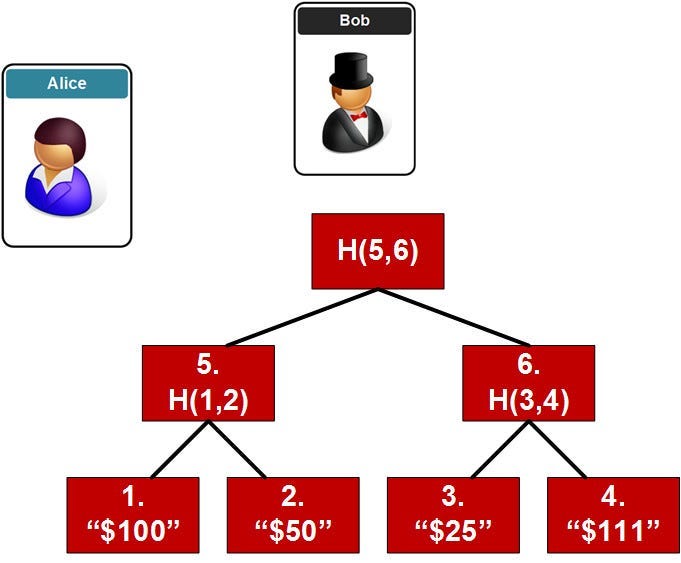
然后，Bob The Bank 会将根哈希发送给 Alice Online，然后她可以检查她是否计算出相同的值。如果他们同意，他们拥有相同的交易集。但是，假设 Alice Online 只是想搜索树的一个分支。我们可以通过仅将计算能力提高 log(N) 来在 Merkle 树中执行此操作 - 其中 N 是树中节点的数量（其中哈希列表会随节点数量而变化）。这样，我们可以检查交易 3 和 4 是否在树中。

这是一个 Merkle 树方法的简单演示：

Merkle 树 本页概述了 Merkle 树的一些示例，其中包含 node.js。Merkle。带有 node.js 的 Merkle 树。Merkle… asecuritysite.com

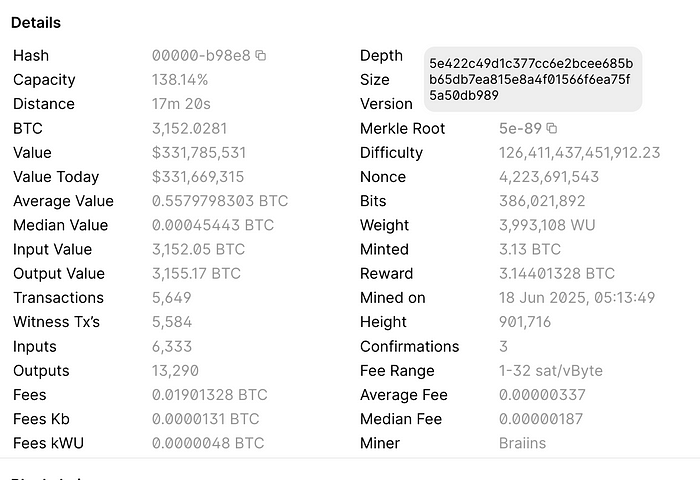
Merkle 树被用于许多应用程序中，包括 P2P 网络，以及比特币交易、Git 分发和 BitTorrent 协议。你还可以在 NoSQL 系统中找到它，例如 Apache Cassandra。另一个新的应用是在后量子密码学中，例如 SPHINCS+。在区块链中，每个块都包含一个 Merkle 树根哈希，它是该特定块中所有交易的哈希[此处]：

经典论文

1977 年提交的一项专利标志着网络安全行业的开始。它是由 Martin Hellman、Whitfield Diffie 和 Ralph Merkle 组成的奇迹团队提交的，其中概述了一种密钥交换方法，该方法允许 Bob 和 Alice 公开通信，并发现一个其他人无法泄露的秘密。虽然该专利包括 Merkle，但它通常被称为 Diffie-Hellman 专利，并且被分配给斯坦福大学[此处]：

这项工作首先发表在 1976 年 11 月发表的 Diffie-Hellman 经典论文中，其中第 8 项权利要求非常突出。在此，该专利概述了一种让各方生成自己的随机值的方式，然后以公开的方式交换这些值，并让各方最终获得相同的共享秘密：

除了 Ralph Merkle 之外，很少有人预料到这项专利的出现，但是通往陷门函数概念的大门已经打开，并且在 Diffie-Hellman 专利之后不久，Hellman-Merkle 专利也随之而来[此处]：

它涵盖了使用背包的陷门方法，并展示了一种创建公钥和私钥的方法。并且其中一种可以被使用，并且只有另一种可以逆转第一种。Shamir 最终创建了一种破解这些的方法，但是该专利是公钥加密的第一个应用。这是一个范围广泛的专利，包含 17 项权利要求，其中前六项定义了公钥加密的核心，包括密钥对的使用以及它可以用于身份验证（其中私钥可以为某些内容签名，而公钥可以证明签名）：

Merkle-Damgård 结构：MD5、SHA-1 和 SHA-2

数据哈希的简单概念奠定了网络安全信任的基础，我们可以获取数据并为数据创建固定长度的哈希。如果我们不能信任我们的哈希方法，那么我们就麻烦了。当我们创建完美的的消息哈希时，因此我们需要确保我们具有：

• 抗碰撞性。 难于找到两个具有相同哈希的消息。因此，我们应该无法在合理的时间内找到两个消息（M1 和 M2）的哈希值相同：H(M1)=H(M2)。
• 抗原像性。 如果我们已经有一个哈希值 (h)，那么应该很难找到一条消息会给出相同的哈希。因此，对于给定的哈希 (h)，很难找到一条消息 (M1) 使得 H(M1)=h。

最初的哈希方法通常基于 Merkle-Damgård (MD) 结构。使用此方法，我们使用数据块创建一个哈希函数。基于 MD 结构，Ron Rivest 开发了 MD5 哈希方法，该方法在业界得到广泛采用。它的工作原理是采用静态初始化向量 (IV)，然后将其输入到单向函数 (f) 中，以及消息块。我们将此输出输入到下一阶段，依此类推，直到我们到达末尾的消息填充：

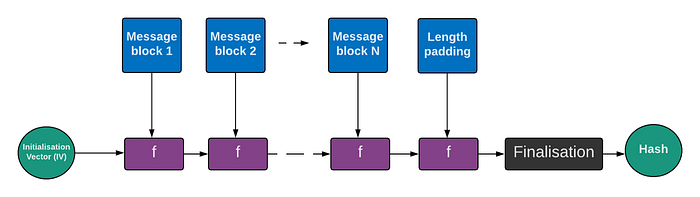
单向函数 (f) 通常会压缩数据并产生比输入的数据更少的位。不幸的是，MD 结构有很多弱点，其中最严重的一个是长度扩展攻击。使用此方法，对手 (Eve) 可以获取未知消息的哈希，然后添加其他数据以生成新的有效哈希。如果你有兴趣，这里有 MD 攻击：

长度扩展攻击 网络安全信任的基础是数据哈希的简单概念，我们可以获取数据并… asecuritysite.com

Ralph 在他的论文中概述了 MD 结构[此处]：

他的公钥方法

背包问题定义了一个问题，即我们有一定数量的权重，并且必须用最少数量的权重来填充我们的背包，使其达到给定的权重。一般来说，问题是：

• 给定一组数字 A 和一个数字 b。
• 找到 A 的子集，其总和为 b（或最接近 b）。

因此，假设你有一组权重，分别为 1、4、6、8 和 15，并且我们想要获得 28 的权重，因此我们可以使用 1、4、8 和 15 (1+4+8+15=28)。

因此，我们的代码将变为 11011（由“1”、“4”、没有“6”、“8”和“15”表示）。

然后，如果我们的纯文本是 10011，背包是 1、4、6、8、15，那么我们的密文是 1+4+8+15，得到 28。

纯文本 00001 将给我们一个密文 15。

使用公钥密码学，我们有两个背包问题。其中一个很容易解决（私钥），另一个很困难（公钥）。

创建公钥和私钥

我们现在可以使用我们的权重创建一个超递增序列，其中当前值大于前面值的总和，例如 {1, 2, 4, 9, 20, 38}。超递增序列使背包问题容易解决，我们取总权重，并将其与最大权重进行比较，如果它大于权重，则它在其中，否则它不在其中。

例如，对于权重 {1,2,4,9,20,38}，值为 54，我们得到：

检查 54 是否适合 38？是（小于 54）。[1] 我们现在有 16 的余额。
检查 16 是否适合 20？否。[0]。
检查 16 是否适合 9？是。[1]。我们现在有 5 的余额。
检查 5 是否适合 4？是。[1]。我们现在有 1 的余额。
检查 1 是否适合 2？否。[0]。
检查 1 是否适合 1？是 [1]。

我们的结果是 101101。

如果我们有一个非超递增背包，例如 {1,3,4,6,10,12,41}，并且必须制作 54，那么它会更加困难。因此，非超递增背包可以是公钥，而超递增背包是私钥。

制作公钥

我们首先从我们的超递增序列开始，例如 {1,2,4,10,20,40}，并取这些值并乘以数字 n，并取一个值（例如 120）的模数 (m)，该值大于总数 (m)。对于 n，我们确保没有任何数字与任何数字有公因子。让我们选择一个 n 值为 53，所以我们得到：

1×53 mod(120) = 53
2×53 mod(120) = 106
4×53 mod(120) = 92
10×53 mod(120) = 50
20×53 mod(120) = 100
40×53 mod(120) = 80

因此公钥是：({53,106,92,50,100,80},53,120)，私钥是 {1, 2, 4, 10, 20,40}。公钥很难分解，而私钥很容易。让我们尝试发送一条二进制代码消息：

111010 101101 111001

我们有六个权重，所以我们将它们分成三组六个权重：

111010 = 53 + 106 + 92 + 100 = 351
101101 = 53+ 92 + 50 + 80 = 275
111001 = 53 + 106 + 92 + 80 = 331

因此，我们的密文是 351 275 331。

接收者已知的两个数字是 120（m - 模数）和 53（n 乘数）。

我们需要 n-1，它是 n mod m 的乘法逆元，即 n(n−1) = 1 mod m。为此，我们找到 n 的逆元：

n-1 = 53-1 mod 120
(53 x _n) mod 120 = 1

因此，我们尝试 (53 x n-1 mod 120) 中的 n-1 值，以便获得 1 的结果：

n-1     结果
1       53
2       106
3       39
...
75      15
76  68
77  1

因此，逆元是 77。[计算]

编码后的消息是 351 275 331，现在很容易计算纯文本：

351×77 mod(120) = 27 = 111010 (1+2+4+20)
275×77 mod(120) = 55 = 101101
331×77 mod(120) = 47 = 111001

因此解码后的消息是：

111010 101101 111001

这与我们的原始消息相同：

111010 101101 111001

解码非常容易，我们唯一需要做的是找到逆元，这并不太困难。

在此处尝试此示例[此处]。

在此 Wiki 页面[此处]，私钥是 {2, 7, 11, 21, 42, 89, 180, 354}，n=792，m=881，数据为 "01100001"，公钥为 {295, 592, 301, 14, 28, 353, 120, 236}，给出的密码为 "1129"。在此处尝试示例[此处]。

结论

对于 Ralph，我对他的智慧和动力表示敬佩。

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～