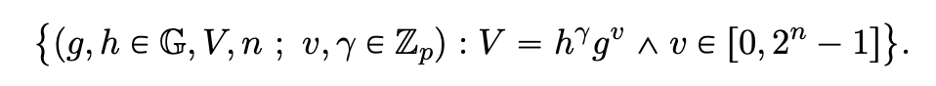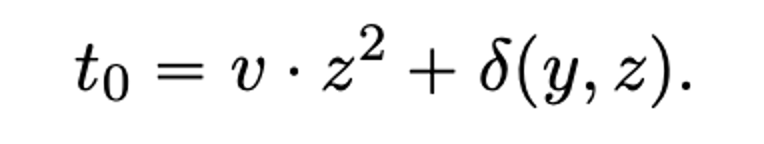Bulletproofs 中的“冰冻之心”漏洞

在本系列的第一部分中，我们披露了破坏零知识证明系统多个实现健全性的严重漏洞。这类我们称之为 Frozen Heart (冰冻之心) 的漏洞，是由 Fiat-Shamir 转换的不安全实现引起的，这些实现允许恶意用户伪造随机声明的证明。在本系列的第二部分中，我们演示了如何利用特定证明系统中的 Frozen Heart 漏洞：Girault 的知识证明。在这篇文章中，我们将演示针对另一个证明系统的类似利用：Bulletproofs。

零知识证明和 Fiat-Shamir 转换

这篇文章假设你对零知识证明有所了解。如果你想了解更多相关信息，可以阅读一些有用的博客文章和视频，例如 Matt Green 的入门文章。要了解更多关于 Fiat-Shamir 转换的信息，请查看我写的博客文章，其中更详细地解释了它。你还可以查看 ZKDocs 以获取有关这两个主题的更多信息。

Bulletproofs

Bulletproofs 是一种复杂而高效的零知识范围证明，其中证明者证明某个秘密值位于预定义的范围内，而无需揭示该值本身。

Bulletproofs 在一种称为 Pedersen commitment 的密码学原语上运行，这是一种特殊的承诺方案。使用承诺方案，一方可以创建一个承诺，将该方绑定到一个秘密值，但不揭示关于该值的任何信息。之后，该方可以解除承诺或揭示此承诺；如果揭示了，并且如果该方案是安全的，则另一方可以确定所揭示的值与原始承诺的值相同。

要为值 x 创建一个 Pedersen commitment，你需要生成一个随机的 gamma，然后使用 comm = (gx)(hgamma) 计算承诺：g 和 h 是你的有限群的不同生成器，并且 h 相对于 g 的离散对数是未知的（即，找到 ga = h 使得 a 是不可行的）。由于 Pedersen commitments 是安全的，因此该承诺不会泄露有关 x 的任何信息，并且不可能在该承诺上含糊其辞；这意味着你不能发布不同的 x’ 和 gamma’ 值来产生相同的承诺（假设 g 和 h 之间的离散对数是未知的）。

Pedersen commitment 不泄露任何信息这一事实对于复杂的协议（例如，需要保证秘密值落在预定义范围内的协议——例如，限制这些值以防止整数溢出）来说可能存在问题。但是，使用 Bulletproofs，我们可以证明我们的承诺对应于预定义范围内的值，例如 [0, 232)，而无需泄露特定的输入值。

不幸的是，Bulletproofs 协议太复杂了，无法在这篇文章中详细介绍。为了描述 Frozen Heart 漏洞，我将逐步介绍 Bulletproofs 协议，但如果你以前没有见过它，这将很难理解。如果你想了解更多关于 Bulletproofs 如何工作的信息，你可以在网上找到许多博客和视频，例如这篇总结。

Bulletproofs 中的 Frozen Heart 漏洞

Bulletproofs 有几个 Fiat-Shamir 转换（确切的数量取决于所使用的参数），这些转换可能以不同的方式被滥用。在本节中，我将介绍如何利用其中一个漏洞。事实上，这个漏洞是原始 Bulletproofs 论文的作者犯的一个错误的结果，他们建议使用不安全的 Fiat-Shamir 实现。ING Bank 的 zkrp、SECBIT Labs 的 ckb-zkp 和 Adjoint, Inc. 的 bulletproofs 都受到了这个问题的影响。

Bulletproofs 在 Pedersen commitments 上运行，其形式为 V = (gv)(hgamma)。提醒一下，Bulletproofs 的目标是证明秘密值 v 位于预定义的范围内。就本文而言，我们将使用 [0, 232) 作为我们的预定义范围。以下是 Bulletproofs 的正式零知识证明声明：

Bulletproofs 的正式证明声明（来源）

在本系列的第一部分中，我们介绍了一个安全实现 Fiat-Shamir 转换的经验法则：Fiat-Shamir 哈希计算必须包括零知识证明声明中的所有公共值和证明中计算的所有公共值（即，所有随机“承诺”值）。因此，我们希望确保此声明中的所有公共值（g、h、V、n）都包含在 Fiat-Shamir 计算中，以及我们尚未介绍的随机承诺。

与大多数密码学论文一样，Bulletproofs 算法以其交互式版本呈现。以下是论文中提出的证明者的角色：

来自原始论文的交互式 Bulletproofs 协议

（为了清楚起见，这不是协议的完整版本。在 Bulletproofs 论文的后面描述了一个重要的优化，以减少步骤(63)中发送的证明的大小，但这与此漏洞无关。）

一旦证明者在步骤(63)中发送了最终证明，验证者将需要通过执行以下检查来验证它：

验证者执行的用于验证 Bulletproofs 的检查（来源）

在证明者协议的步骤 (49)/(50) 和 (55)/(56) 中，需要生成三个不同的 Fiat-Shamir 挑战值：x、y 和 z。但是，作者建议使用不安全的计算来计算这些值：

原始 Bulletproofs 论文中推荐的不安全 Fiat-Shamir 挑战计算（来源）

根据作者的说法，我们应该设置 y = Hash(A,S)，z = Hash(A,S,y)，并且（按照他们的描述）x = Hash(A,S,y,z,T1,T2)。这违反了我们的经验法则：声明中的任何公共值（最重要的是 V）都不包括在内。这是一个 Frozen Heart 漏洞! 这个漏洞非常严重；正如你可能已经猜到的那样，它允许恶意证明者伪造实际上位于预定义范围之外的值的证明。

现在，要真正利用这一点，恶意证明者可以执行以下操作：

• 将 v 设置为范围内的任何值。所以我们假设 v = 3。
• 选择一个随机的 gamma 值。
• 使用这些 v 和 gamma 值，按照预期（分别根据步骤 (41)、(42)、(44) 和 (47)）生成 aL、aR、A 和 S。
• 按照 Bulletproofs 论文中的描述计算 t1 和 t2（这不在上图中，但在论文的文本中描述），然后通过随机生成数字来计算值 t1’ 和 t2’。在计算 T1 和 T2 时，将 t1 替换为 t1’，将 t2 替换为 t2’。因此，为了清楚起见，我们设置 Ti = (gt’_i)(htau_i)（如预期的那样，但我们将 ti 替换为 ti’）。
• 根据协议计算其余值（l、r、t_hat、tau_x、mu）。
• 最后，使用相同的 gamma 但使用新的 v’ 值来计算新的 V。具体来说，设置 v’ = 3 + (t1 - t’1)(x/z2) + (t2 - t’2)(x2/z2)（你将在一秒钟内明白为什么这样选择）。在这里，3 来自于在步骤 1 中设置 v = 3。

现在，回想一下上面的所有验证检查。我们计算方式与预期不同的唯一值是 T1、T2 和 V。由于我们按照预期计算了其他值，因此除了检查 (65) 之外，所有检查都将自动通过，检查 (65) 依赖于 T1、T2 和 V。但是由于 x、y 和 z 的计算独立于 V，因此我们可以计算依赖于这些值并且可以通过检查 (65) 的恶意 V 值。让我们看看这是如何运作的：

首先，让我们简化检查 (65) 的左侧：

LHS = (gt_hat)(htau_x) = (g[t0 + t1 * x + t2 * x2])(h[tau2 * x2 + tau1 * x + z2 * y])

现在，让我们简化检查 (65) 的右侧：

RHS = (Vz2)(gdelta(y,z))(T1x)(T2x2) = (Vz2)(gdelta(y,z))[(gt’1)(htau1)]x[(gt’2)(htau2)]x2

现在，如果你看一下我们为 V 选择的 v’ 值，你会发现 g 中的 T1 和 T2 指数将抵消 V 的 g 中的指数。所以右侧简化如下：

= g[3z2 + t1 * x + t2 * x2 + delta(y,z)]h[gamma * z2 + tau1 * x + tau2 * x2]

我们可以看到 h 中的指数在两侧是相同的。我们现在要做的就是检查 g 中的指数是否匹配。

在左侧 g 指数中，我们有 t0 + t1 * x + t2 * x2。

在右侧 g 指数中，我们有 3z2 + delta(y,z) + t1 * x + t2 * x2。

并且 t0 在原始论文中定义为：

t0 在 Bulletproofs 论文中定义（来源）

这完全正确，这意味着我们已成功伪造了证明。

为了清楚起见，这是一个伪造，因为我们刚刚为新计算的 V 值提交了这个证明，其中 v 设置为 v’ = 3 + (t1 - t’1)(x / z2) + (t2 - t’2)(x2 / z2)。由于 x 和 z 是随机的 Fiat-Shamir 挑战，v’ 最终将成为区间 [0, group order) 中的一个随机值。由于 group order 通常比有问题的区间大得多（这里是 232），因此 v’ 将是一个超出范围的值，并且具有压倒性的概率，但证明仍然会通过。如果由于任何原因 v’ 不在此范围之外，则恶意参与者可以简单地使用新的随机值（例如，新的 gamma、新的 t’1 等）重新开始相同的过程，直到获得所需的 v’ 值为止。

Frozen Heart 对 Bulletproofs 的影响

Frozen Heart 漏洞非常严重，因为它们允许攻击者伪造证明，但它们对周围应用程序的影响取决于应用程序如何使用证明系统。正如我们在本系列的第二部分中看到的 Schnorr 和 Girault 证明系统一样，在某些情况下，这些漏洞可能并不严重。但是，对于 Bulletproofs 而言，这种情况不太可能发生。

在我们的示例中，我们能够为 group order 中的一个随机值生成一个伪造。在大多数应用程序中，范围证明的预定义范围通常比 group order 的大小小得多。这意味着，虽然无法选择特定值，但攻击者可以轻松地为超出所需范围的值生成证明。在我们见过的大多数使用 Bulletproofs 的情况下，这都是非常严重的。

请关注本系列的最后一部分，在其中我们将探讨更复杂的证明系统 PlonK 中的 Frozen Heart 漏洞。

• 原文链接： blog.trailofbits.com/202...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～