GKR协议实现：代码深度解析

介绍

GKR (Goldwasser–Kalai–Rothblum) 协议提供了一种有效的方法来验证算术电路上的计算，避免了重新执行并减少了验证者的工作。在我们之前的文章 GKR 协议：一个循序渐进的例子 中，我们详细探讨了该协议的工作原理，重点关注其数学结构，并通过一个具体的手工示例进行了演示。GKR 目前用于提高 lookup arguments 的性能，这对于证明零知识虚拟机的执行至关重要。

本文的目标是解释我们在 Lambdaworks 中对该协议的 实现，展示如何描述和验证算术电路，以及证明者和验证者如何在实践中运作。我们还将看到如何应用 Fiat-Shamir 变换 使协议 非交互式，以及如何调整 Sumcheck 协议 并将其集成作为验证每个电路层的核心组件。

如果你不熟悉该协议或需要复习，我们建议从上面链接的我们之前的文章开始。

警告： 这里介绍的 GKR 实现仅用于教育目的，不应在生产中使用。请注意，对于更通用的电路，该协议容易受到实际攻击，因为它依赖于 Fiat-Shamir 变换（参见 "How to Prove False Statements"）。

电路结构

GKR 电路由多层组成。每一层包含门，每个门操作前一层的输出。门可以是加法或乘法。为了协议兼容性，每一层必须有 2 的幂次个门。

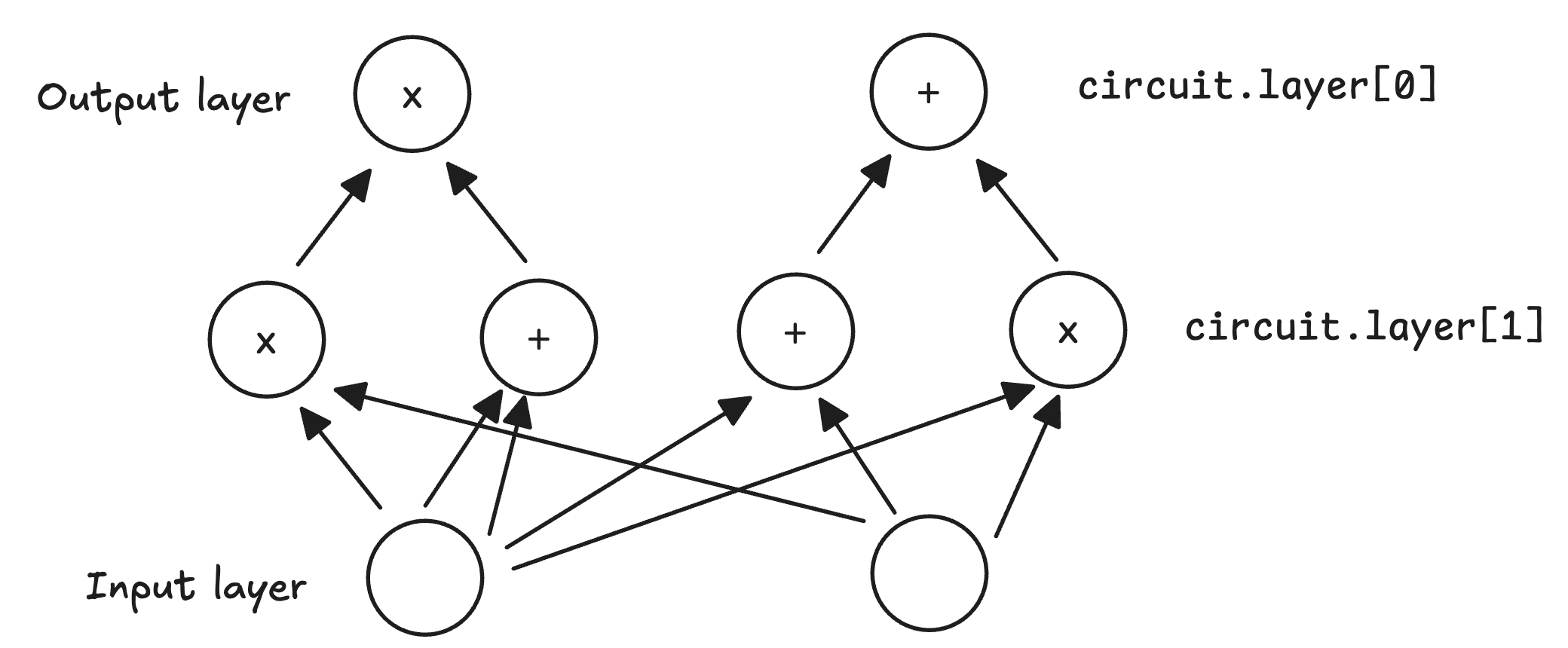
在之前的文章中用作示例的算术电路

在某些情况下，如果所有门都是乘法，我们可以使用更有效的版本。

电路 API

用于电路构建的主要结构是：

• Circuit —— 由一个层向量（从上到下排序，从输出层开始，不包括输入层）；输入数量；以及索引输入层所需的变量数量组成。

pub struct Circuit {
      /// 第一层是输出层。它不包括输入层。
      layers: Vec<CircuitLayer>,

      /// 输入数量
      num_inputs: usize,
      input_num_vars: usize, // 输入数量的 log2
}

• CircuitLayer —— 包含一个门向量和索引这些门所需的变量数量。

pub struct CircuitLayer {
      pub gates: Vec<Gate>,
      pub num_of_vars: usize, // 这一层中门数量的 log2
}

• Gate —— 单个门，带有其类型和输入索引。
• GateType —— Add 或 Mul。

电路门

电路中的每个门都是加法（Add）或乘法（Mul）门。门类型决定了如何组合前一层的输出：

• Add: 门输出其两个输入线之和。
• Mul: 门输出其两个输入线之积。

例如：

let gate_1 = Gate::new(GateType::Mul, [0, 1]); // 将前一层索引 0 和 1 的输出相乘。
let gate_2 = Gate::new(GateType::Add, [2, 3]); // 将前一层索引 2 和 3 的输出相加。

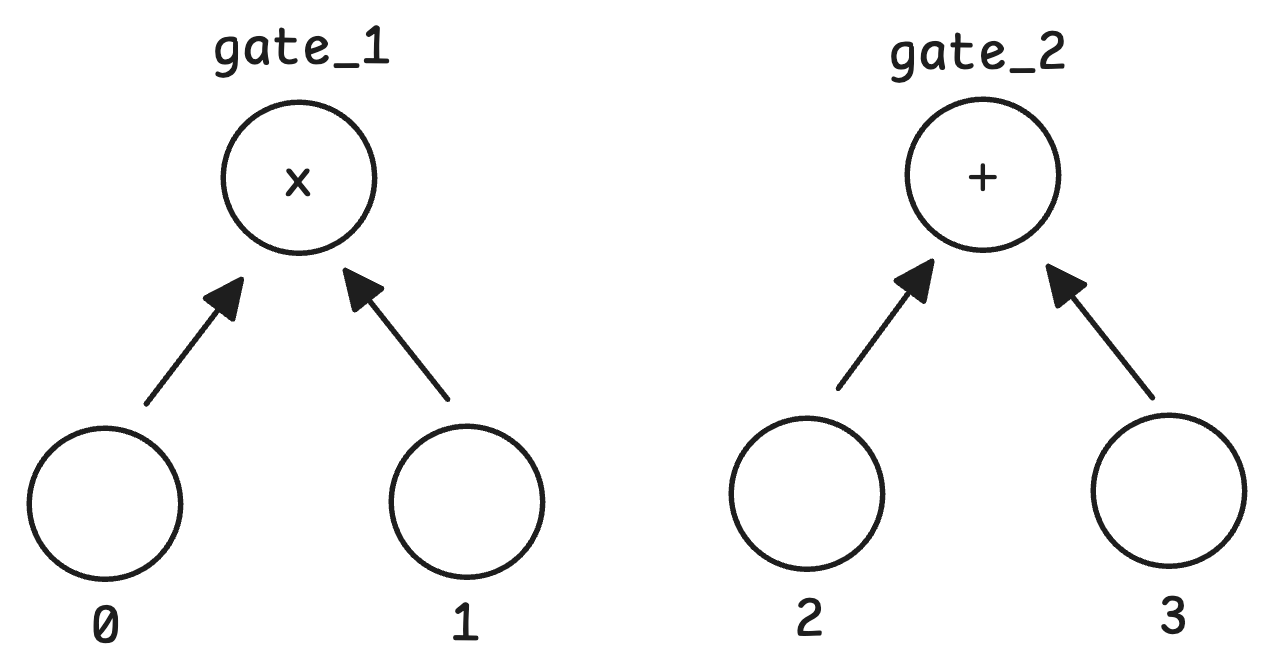
示例：博客文章电路

为了说明这一点，让我们逐步构建我们在 循序渐进的 GKR 博客文章 中使用的确切电路。这在代码库中作为 lambda_post_circuit() 提供，你可以直接使用它或将其用作电路的模板。

pub fn lambda_post_circuit() -> Result<Circuit, CircuitError> {
    use crate::circuit::{Circuit, CircuitLayer, Gate, GateType};
    Circuit::new(
        vec![
            // 第 0 层（输出层）：两个门
            CircuitLayer::new(vec![
                Gate::new(GateType::Mul, [0, 1]), // 将前一层索引 0 和 1 的输出相乘
                Gate::new(GateType::Add, [2, 3]), // 将前一层索引 2 和 3 的输出相加
            ]),
            // Layer1：四个门
            CircuitLayer::new(vec![
                Gate::new(GateType::Mul, [0, 1]), // 将两个输入相乘
                Gate::new(GateType::Add, [0, 0]), // 将第一个输入加到自身
                Gate::new(GateType::Add, [0, 1]), // 将两个输入相加
                Gate::new(GateType::Mul, [0, 1]), // 再次将两个输入相乘
            ]),
        ],
        2, // 两个输入
    )
}

如何构建你的电路

1. 确定输入数量。 每个输入都将通过其索引（从 0 开始）引用。
2. 构建第一层： 第一层中的每个门都对输入进行操作。使用 Gate::new(GateType::Add, [i, j]) 或 Gate::new(GateType::Mul, [i, j]) 添加或乘以输入索引 i 和 j。
3. 构建后续层： 每个门都对前一层的输出进行操作。索引始终引用前一层的输出顺序。每个新层都应插入 layers 向量的开头，因为层从电路的顶部（输出层）到底部排序。
4. 重复直到到达输出层。
5. 将你的层包装在 Circuit::new(layers, num_inputs) 调用中。

重要提示：

• 每一层必须有 2 的幂次个门。
• 索引必须有效（即，不超出前一层的范围）。

电路自动验证

当你构建 Circuit 时，会自动执行多项检查以确保电路格式良好：

• 2 的幂次个门： 每一层必须有 2 的幂次个门。这是协议有效工作所必需的。
• 有效的输入索引： 每个门的输入索引必须引用前一层的有效输出。如果索引超出范围，则构造失败。
• 2 的幂次个输入： 电路输入的数量也必须是 2 的幂次。

如果未能满足任何这些条件，构造函数将返回一个描述性错误（作为 Result::Err）。这可以防止创建无效电路，并有助于在开发的早期发现错误。

GKR 协议

让我们看看协议的每个步骤是如何在我们的代码中实现的。我们的目标是演示它如何利用 sumcheck 协议将关于电路一层计算正确性的声明递归地减少到关于下一层的声明，从输出层向下进行到输入层。

回想一下，在我们的实现中，我们利用 Fiat-Shamir 变换使协议成为非交互式的，这导致它与上一篇文章中描述的版本略有不同。

证明者

证明结构

证明者负责评估电路并构建一个证明，使验证者确信该评估的正确性。证明者的核心逻辑位于 prover.rs 中，你可以在其中找到由以下内容组成的结构 GKRProof：

• 电路的输入值和输出值。
• 每个电路层的 sumcheck 证明，包括：
  • 轮次单变量多项式 gjgj。
  • 单变量多项式 qq 的组成。

让我们回顾一下多项式 gjgj 和 qq 是什么。在每个电路层 ii 中，对于其 sumcheck 的每一轮 jj，证明者必须通过固定第一个变量并对所有其他变量求和来计算单变量多项式 gjgj。例如，在我们之前的文章中，在第 00 层中，sumcheck 有四轮，导致以下多项式：

g1(z)=∑(b2,c1,c2):∈0,13~f(0)r0(z,b2,c1,c2),g2(z)=∑(c1,c2):∈0,12~f(0)r0(s1,z,c1,c2),g3(z)=∑c2:∈0,1~f(0)r0(s1,s2,z,c2),g4(z)=~f(0)r0(s1,s2,s3,z),g1(z)=∑(b2,c1,c2):∈0,13f~r0(0)(z,b2,c1,c2),g2(z)=∑(c1,c2):∈0,12f~r0(0)(s1,z,c1,c2),g3(z)=∑c2:∈0,1f~r0(0)(s1,s2,z,c2),g4(z)=f~r0(0)(s1,s2,s3,z),

其中 sjsj 是随机挑战。

另一方面，对于每一层 ii，多项式 qq 是组合 q=~Wi+1∘ℓq=W~i+1∘ℓ，其中 ~Wi+1W~i+1 是将节点位置映射到其实际值的函数的多线性多项式扩展，ℓℓ 是从 b⋆b⋆ 到 c⋆c⋆ 的线。在之前的例子中，ℓ(0)=(s1,s2)ℓ(0)=(s1,s2) 并且 ℓ(1)=(s3,s4)ℓ(1)=(s3,s4)。

在代码库中，你会看到它显示为：

pub struct GKRProof<F: IsField> {
    pub input_values: Vec<FieldElement<F>>,
    pub output_values: Vec<FieldElement<F>>,
    pub layer_proofs: Vec<LayerProof<F>>,
}

每个电路层的证明是：

pub struct LayerProof<F: IsField> {
    pub sumcheck_proof: GKRSumcheckProof<F>,
    pub poly_q: Polynomial<FieldElement<F>>,
}

最后，sumcheck_proof 包含轮次多项式 gjgj 和这些轮次中使用的挑战，以便证明者和验证者都可以计算直线 ℓℓ。

pub struct GKRSumcheckProof<F: IsField> {
    pub round_polynomials: Vec<Polynomial<FieldElement<F>>>,
    pub challenges: Vec<FieldElement<F>>,
}

构建证明

证明者使用 Prover::generate_proof() 方法构造证明。此函数接收电路及其输入，对它们进行评估，并生成证明。让我们将此函数分解为以下步骤：

1. 电路评估： 证明者在给定的输入上评估整个电路。

let evaluation = circuit.evaluate(input);

2. 转换初始化：

由于我们实现了协议的非交互式版本，因此证明者必须提交到电路、其输入和其输出。这是通过定义一个 DefaultTranscript 来完成的，我们可以从中提交和采样新值。证明者和验证者都将此数据附加到转换中。为了附加电路，他们需要将其转换为字节，他们使用可以在 lib.rs 文件中找到的函数 circuit_to_bytes() 来完成。我们稍后将在 Fiat-Shamir 小节中看到更多关于转换的信息。

3. 采样 r0r0：

证明者采样第一个 r0r0 以固定变量 aa 并开始 sumcheck。回想一下，变量 aa 可能有多个比特，因此 r0r0 的大小与 aa 称为 k0k0 的大小相同

let k_0 = circuit.num_vars_at(0).ok_or(ProverError::CircuitError)?;
let mut r_i: Vec<FieldElement<F>> = (0..k_0)
       .map(|_| transcript.sample_field_element())
       .collect();

4. Sumcheck 层迭代： 对于每一层，证明者按照以下步骤应用 sumcheck 协议：

   • 构建函数：

   证明者构建他想要应用 sumcheck 的函数，

   ~fri(b,c)=˜add_i(ri,b,c)⋅(˜Wi+1(b)+˜Wi+1(c))+˜mul_i(ri,b,c)⋅(˜Wi+1(b)⋅˜Wi+1(c)),f~ri(b,c)=add_i~(ri,b,c)⋅(W~i+1(b)+W~i+1(c))+mul_i~(ri,b,c)⋅(Wi+1~(b)⋅Wi+1~(c)),

   使用方法 Prover::build_gkr_polynomial()。请注意，此方法返回两个项而不是仅仅一个项。更具体地说，它返回一个包含 2 个项目的向量，这些项目本身就是两个多线性多项式的向量：

   第一项或向量：

   [˜add_i(ri,b,c),˜Wi+1(b)+˜Wi+1(c)][add_i~(ri,b,c),Wi+1~(b)+Wi+1~(c)]

   第二项或向量：

   [˜mul_i(ri,b,c),˜Wi+1(b)⋅˜Wi+1(c)][mul_i~(ri,b,c),Wi+1~(b)⋅Wi+1~(c)]

   这是必要的，因为 lambdaworks 的 sumcheck 实现只接受多线性多项式的乘积。这就是为什么我们将多项式 ~frif~ri 分成两个多线性多项式乘积的项。

let gkr_poly_terms =
             Prover::build_gkr_polynomial(circuit, &r_i, w_next_evals, layer_idx)?;

- **应用 GKR Sumcheck 证明者：**

我们使用专门为 GKR 协议设计的 sumcheck 实现。我们稍后将更详细地讨论这个新的 sumcheck，但有三个**关键变化**要记住：

**I)** 我们需要一个 **将转换作为输入** 的 sumcheck 证明者，因此我们可以为证明者和验证者保持相同的转换，该转换在开始时创建。

**II)** 这个新的 sumcheck 也 **返回执行期间采样的随机值**。这允许证明者和验证者稍后计算函数 ℓℓ，该函数依赖于这些值。

**III)** GKR sumcheck 允许我们**同时处理** ~fri(b,c)f~ri(b,c) 的**两项**。

let sumcheck_proof = gkr_sumcheck_prove(gkr_poly_terms, &mut transcript)?;

- **Sumcheck 最终声明：**

证明者抽取一个新的域元素 r⋆r⋆（在代码中称为 `r_new`），在其上评估直线 ℓℓ，并计算组合多项式 qq。ℓℓ 的评估使用可以在 `lib.rs` 中找到的函数 `line()` 计算 (因为它被证明者和验证者使用)。另一方面，多项式 qq 使用方法 `Prover::build_polynomial_q()` 计算。为了计算这个多项式，证明者需要插入三个点，因为 qq 的度数为 2（因为 ℓℓ 是线性的，而 ~Wi+1W~i+1 在每个变量中都是多线性的）。

// r* 在我们的博客文章 <https://learnblockchain.cn/article/13911/> 中
let r_new = transcript.sample_field_element();

// 使用直线函数构造下一轮的随机点
//  l(x) = b + x * (c - b)
let (b, c) = sumcheck_challenges.split_at(num_vars_next);
// r_i = l(r_new)
r_i = crate::line(b, c, &r_new);

let poly_q = Prover::build_polynomial_q(b, c, w_next_evals.clone())?;

5. 制作证明： 最后，证明者拥有制作证明的所有要素。

let proof = GKRProof {
       input_values: input.to_vec(),
       output_values,
       layer_proofs,
};

验证者

一旦我们理解了证明者的行为，就很容易看到验证者需要做什么。它只需遵循与证明者相同的步骤，使用证明的元素并在每个步骤执行必要的检查。她使用方法 Verifier::verify() 验证证明，步骤如下：

1. 转换初始化：

与证明者一样，首先创建一个转换并附加电路（双方都知道）、输入和证明者在证明中发送的输出。

2. 初始和计算：

为 r0r0 采样域元素以固定变量 aa 并将初始和设置为 m0=~D(r0)m0=D~(r0)，其中 ~DD~ 是将输出门映射到评估值的函数的多线性多项式扩展。证明者将这些值作为证明的一部分发送。

let output_poly_ext = DenseMultilinearPolynomial::new(proof.output_values.clone());
let mut claimed_sum = output_poly_ext
       .evaluate(r_i.clone())
       .map_err(|_e| VerifierError::MultilinearPolynomialEvaluationError)?;

3. 逐层验证： 对于每一层 ii，验证者执行以下操作：

   • 验证 sumcheck 证明：

   验证者使用函数 gkr_sumcheck_verify 检查当前层的 sumcheck 证明。此函数确保证明者提供的一系列单变量多项式 gjgj 的度数为 2，并且与每个 sumcheck 轮次 jj 中声明的和一致；也就是说，

   deg(gj)≤2,deg(gj)≤2,gj(0)+gj(1)==gj−1(sj−1).gj(0)+gj(1)==gj−1(sj−1).

let (sumcheck_verified, sumcheck_challenges) = gkr_sumcheck_verify(
 claimed_sum.clone(),
 &layer_proof.sumcheck_proof,
 &mut transcript,
 )?;
if !sumcheck_verified {
 return Ok(false);
}

- **使用组合多项式 qq检查最后一轮 nn：**

为了验证 sumcheck 在最后一轮中的最终声明，验证者需要值 ~Wi+1(b⋆)W~i+1(b⋆) 和 ~Wi+1(c⋆)W~i+1(c⋆)。但是，验证者不知道多项式 ~Wi+1W~i+1：验证者没有电路评估。这就是她使用证明者提供的组合多项式 qq 执行最终检查的原因。回想一下，如果证明者没有作弊，则 q(0)=~Wi+1(b⋆)q(0)=W~i+1(b⋆) 并且 q(1)=~Wi+1(c⋆)q(1)=W~i+1(c⋆)。因此，验证者必须检查

gn(sn)=˜add\_i(ri,b⋆,c⋆)⋅(q(0)+q(1))+˜mul\_i(ri,b⋆,c⋆)⋅(q(0)⋅q(1))gn(sn)=add\_i~(ri,b⋆,c⋆)⋅(q(0)+q(1))+mul\_i~(ri,b⋆,c⋆)⋅(q(0)⋅q(1))

let last_poly = layer_proof.sumcheck_proof.round_polynomials.last().unwrap();
let last_challenge = sumcheck_challenges.last().unwrap();
let expected_final_eval = last_poly.evaluate::<F>(last_challenge);

let q_at_0 = layer_proof.poly_q.evaluate(&FieldElement::zero());
let q_at_1 = layer_proof.poly_q.evaluate(&FieldElement::one());

let add_eval = circuit.add_i_ext(&r_i, layer_idx).evaluate(sumcheck_challenges.clone())?;
let mul_eval = circuit.mul_i_ext(&r_i, layer_idx).evaluate(sumcheck_challenges.clone())?;

let final_eval = add_eval * (&q_at_0 + &q_at_1) + mul_eval * q_at_0 * q_at_1;
if final_eval != expected_final_eval {
 return Ok(false);
}

- **采样一个新的挑战并更新评估点：**

验证者从转换中采样一个新的域元素 r⋆r⋆，然后使用直线函数计算下一层的下一个评估点 ri+1=ℓ(r⋆)ri+1=ℓ(r⋆)。通过在新的挑战上评估组合多项式 qq 来更新声明的和：q(r⋆)q(r⋆)。

let r_new = transcript.sample_field_element();
let num_vars_next = circuit.num_vars_at(layer_idx + 1).ok_or(VerifierError::CircuitError)?;
let (b, c) = sumcheck_challenges.split_at(num_vars_next);
r_i = crate::line(b, c, &r_new);
claimed_sum = layer_proof.poly_q.evaluate(&r_new);

4. 最终输入检查：

在处理完所有层之后，验证者检查最终声明的和是否与最终评估点 riri 处输入值的多线性扩展的评估匹配。在之前的文章示例中，这将是 q(r⋆)==~W2(r2).q(r⋆)==W~2(r2)。这确保了整个计算从输出到输入都是一致的。

let input_poly_ext = DenseMultilinearPolynomial::new(proof.input_values.clone());
if claimed_sum
       != input_poly_ext
           .evaluate(r_i)
           .map_err(|_| VerifierError::MultilinearPolynomialEvaluationError)? {
               return Ok(false);
}

如果所有检查都通过，则验证者接受证明为有效。否则，证明将在第一次失败的检查时被拒绝。此过程允许验证者有效地确认计算的正确性，而无需重新执行整个电路。

Sumcheck 协议

Sumcheck 协议是 GKR 协议的核心组件。它的作用是允许证明者说服验证者，多线性多项式乘积的和是正确的，而无需验证者直接计算总和。这是通过将原始和减少为单变量多项式检查序列来实现的，每个变量一个。

快速回顾：正在检查的总和是什么？

在 GKR 协议的每一层 ii 中，证明者和验证者需要检查以下形式的和：

S=∑x1,…,xn∈0,1~fri(x1,…,xn)S=∑x1,…,xn∈0,1f~ri(x1,…,xn)

其中 ~fri(x1,…,xn)f~ri(x1,…,xn) 是一个多线性多项式，它编码了该层电路的连线和值，而 nn 是该层的变量数（这取决于索引下一层门所需的比特数）。

sumcheck 协议允许证明者通过发送单变量多项式序列 g1,g2,…,gng1,g2,…,gn 来说服验证者声明的值 SS 是正确的，这样，在第 jj 轮：

gj(z)=∑xj+1,…,xnfr(s1,…,sj−1,z,xj+1,…,xn)gj(z)=∑xj+1,…,xnfr(s1,…,sj−1,z,xj+1,…,xn)

其中 s1,…,sj−1s1,…,sj−1 是在前几轮中采样的挑战, zz 是当前回合的变量，其余变量被求和。轮数（因此 gjgj 多项式的数量）始终等于 ~frif~ri 被检查层的变量数。

在每一轮中，验证者都会检查关键的 sumcheck 属性：

deg(gj)≤2deg(gj)≤2

gj(0)+gj(1)=previous sumgj(0)+gj(1)=previous sum

然后为下一轮采样一个新的挑战 sjsj。经过所有回合后，验证者只剩下关于 fr(s1,…,sn)fr(s1,…,sn) 的声明，该声明将根据下一层进行检查。

拆分sumcheck的GKR多项式

GKR多项式 ~fri(b,c)f~ri(b,c) ，它编码了相邻两层之间的关系，由以下给出：

~fri(b,c)=˜add_i(ri,b,c)⋅(Wi+1(b)+Wi+1(c))+˜mul_i(ri,b,c)⋅(Wi+1(b)⋅Wi+1(c))f~ri(b,c)=add_i~(ri,b,c)⋅(Wi+1(b)+Wi+1(c))+mul_i~(ri,b,c)⋅(Wi+1(b)⋅Wi+1(c))

为了应用 sumcheck 协议，这个多项式被分成两项，每一项都是两个多线性多项式的乘积：

• 第一项：

˜add_i(ri,b,c)⋅(Wi+1(b)+Wi+1(c))add_i~(ri,b,c)⋅(Wi+1(b)+Wi+1(c))

• 第二项：

˜mul_i(ri,b,c)⋅(Wi+1(b)⋅Wi+1(c))mul_i~(ri,b,c)⋅(Wi+1(b)⋅Wi+1(c))

这种拆分是必要的，因为 sumcheck 实现需要多线性多项式的乘积。在代码中，这是由函数 Prover::build_gkr_polynomial 处理的（参见 [Prover 部分] (https://blog.lambdaclass.com/gkr-protocol-implementation-deep-dive-into-the-code/#prover)），该函数返回一个带有两个条目的vector，每个条目都是两个多线性多项式的vector(每个项的因子)。然后将这些传递给 sumcheck 证明者，后者在每一轮中一起处理这两个项。

代码库中的实现

sumcheck 协议的逻辑在 sumcheck.rs 中实现。此文件包含证明者和验证者用于为每个电路层执行 sumcheck 轮的函数。

证明者：逐步 sumcheck 证明生成：

在每一层，证明者按如下方式构造 sumcheck 证明：

1. 构建 GKR 多项式项

对于当前层，构造 GKR 多项式并将其拆分为协议所需的两个项：

let factors_term_1 = terms[0].clone();
let factors_term_2 = terms[1].clone();

let mut prover_term_1 = Prover::new(factors_term_1)?;
let mut prover_term_2 = Prover::new(factors_term_2)?;

2. 计算初始声明的和

证明者计算两个项的初始和并将它们相加：

let claimed_sum_term_1 = prover_term_1.compute_initial_sum()?;
let claimed_sum_term_2 = prover_term_2.compute_initial_sum()?;
let claimed_sum = claimed_sum_term_1 + claimed_sum_term_2;

3. 逐轮应用 sumcheck 协议

对于每一轮，证明者计算每一项的单变量多项式，将它们相加并将结果附加到转换中。每个结果多项式 gjgj 都收集在一个vector中：

let mut proof_polys = Vec::with_capacity(num_vars);
for j in 0..num_vars {
    let g_j_term_1 = prover_term_1.round(current_challenge.as_ref())?;
    let g_j_term_2 = prover_term_2.round(current_challenge.as_ref())?;
    let g_j = g_j_term_1 + g_j_term_2;
    // ...将 g_j 附加到转换中...
    proof_polys.push(g_j);
    // ...采样挑战，更新 current_challenge...
}

4. 收集证明数据

经过所有回合后，多项式vector和挑战用于构造 sumcheck 证明对象：

let sumcheck_proof = GKRSumcheckProof {
    round_polynomials: proof_polys,
    challenges,
};

5. 发送给验证者

将 sumcheck 证明作为整个 GKR 证明的一部分包含在内，验证者将在下一阶段检查该证明。

验证者：逐步 sumcheck 验证：

在每一层，验证者按如下方式处理 sumcheck 证明：

1. 对于每一轮，检查degree和和属性

对于收到的每个单变量多项式 gjgj，检查 degree 是否最多为 2，并且它在 0 和 1 处的评估之和是否与预期值(初始声明或先前挑战中评估的先前多项式)匹配：

// 检查 g_j 的 degree 是否超过理论界限
if g_j.degree() > 2 {
    return Err(crate::verifier::VerifierError::InvalidDegree);
}
let g_j_0 = g_j.evaluate::<F>(&FieldElement::zero());
let g_j_1 = g_j.evaluate::<F>(&FieldElement::one());
let sum_evals = &g_j_0 + &g_j_1;

let expected_sum = if j == 0 {
    claimed_sum.clone()
} else {
    let prev_poly = &proof_polys[j - 1];
    let prev_challenge = &challenges[j - 1];
    prev_poly.evaluate::<F>(prev_challenge)
};

if sum_evals != expected_sum {
    return Ok((false, challenges));
}

2. 更新转换并采样下一个挑战

在每一轮之后，验证者将多项式附加到转换并采样下一个挑战：

let r_j = transcript.sample_field_element();
challenges.push(r_j.clone());

3. 接受或拒绝

如果所有回合都通过检查，则接受总和为正确，而无需直接评估完整总和。如果任何检查失败，请立即拒绝该证明。

sumcheck 协议的每一轮都将变量数减少一个，从而将多元和转换为单变量检查序列。证明者执行主要的计算，而验证者只需要检查少量的多项式评估和域运算。Fiat-Shamir 转换的使用确保了该协议是非交互式的，所有挑战都来自转换。

Fiat-Shamir 转换：使其非交互式

最初的 GKR 协议是交互式的，这意味着它需要在证明者和验证者之间进行一系列来回通信。虽然交互式证明在理论上是合理的，但由于延迟和通信开销，它们对于许多实际应用程序来说是不切实际的。Fiat-Shamir 转换是一种加密技术，用于将交互式证明系统转换为非交互式证明系统。

如何应用 Fiat-Shamir

在我们的实现中，Fiat-Shamir 转换用加密哈希函数(特别是来自 lambdaworks_crypto crate 的 DefaultTranscript) 的输出替换了验证者的随机挑战。这允许证明者确定性地生成所有必要的挑战，而无需与验证者进行任何交互。

1. 转换初始化: 创建转换并使用与证明相关的公共信息进行播种。这包括：

   • 电路结构 (通过 circuit_to_bytes(circuit) 序列化)。
   • 公共输入值。
   • 声明的输出值。

通过包含此信息，任何一方都可以重建相同的转换并验证生成的挑战。

2. 挑战生成: 在交互式协议需要验证者的随机挑战的每个步骤中，该实现改为：
   • 将证明的当前状态(例如，证明者发送的多项式的系数)追加到转换。
   • 使用 transcript.sample_field_element() 从转换中采样一个随机域元素。此元素是从转换中的所有先前信息以加密方式导出的，从而使证明者在提交相关信息之前无法预测它。

关键挑战点

Fiat-Shamir 转换应用于 GKR 协议中的几个关键时刻：

• 初始随机值 (r0r0)：对于输出层，采样初始随机 challenges 以开始逐层归约。
• Sumcheck Challenges (sjsj)：在 Sumcheck 协议的每一轮中，challenges 从 transcript 生成。这些 challenges 对于验证者检查证明者的单变量多项式的一致性至关重要。
• 线函数参数 (r⋆r⋆ 或 r_new)：在每一层的 sumcheck 之后，会采样一个新的 challenge r_new。这个 challenge 用于 line 函数中，以推导出下一层声明和的求值点，有效地连接证明中的各层。

通过利用 Fiat-Shamir 变换，我们的 GKR 实现实现了非交互性，使其更适用于 prover 和 verifier 之间连续通信可能不可行或引入不希望的延迟的实际应用。这种转换是许多现代零知识证明系统的基石，能够在各种场景中实现高效且可验证的计算。

总结

在这篇文章中，我们展示了我们如何实现 GKR 协议。从电路描述开始，证明者评估每一层，构建相应的多项式，并运行定制的 Sumcheck 协议，该协议的 challenges 通过 Fiat-Shamir transcript 生成。验证者使用相同的 transcript，重放 Sumcheck 轮次，使用组合多项式 qq 检查最终声明，并最终确认计算是正确的，一直到公共输入。这样，潜在的昂贵的电路重新执行被简化为一系列轻量级的代数检查。

虽然此实现旨在用于教育用途，但它捕获了协议的每个关键步骤。

• 原文链接： blog.lambdaclass.com/gkr...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～