Binius证明系统，PCS

TL;DR（太长不看版）

Binius 证明系统是一种基于二叉塔的 ZK 证明系统，它提供了小的内存占用和高效的域计算。我们以直观但严格的方式分析了 Binius 中的 PCS，它是任何 ZK 证明系统的基本组成部分。我们介绍了 Binius 中使用的 PCS 的动机，然后分析了 commitment、环切换（ring switch）、多变量sum-check协议（Multi-variate Sumcheck protocol）、FRI，它们用于打开 commitment 的证明。

1. 定义与动机

PCS Commit（PCS 承诺）

与跟踪或 witness 相对应的多项式 t(X) 包含敏感信息，并且大小相对较大（由于其高阶数）。为了在证明过程中实现 ZKSNARK（零知识简洁非交互式知识论证），我们不能直接在证明中包含该多项式（例如，它的系数）。相反，多项式的系数被压缩以产生一个较小的值（例如，一个 256 位的哈希）。

这个值被称为 commitment 值，而这个过程被称为 commit 计算。

例如，在 RISC0 中，对于给定的多项式 ( t )，在 commitment 域上执行 NTT（数论变换）以获得 Merkle 树的叶子节点，然后构建该树，树的根作为 commitment 值。

PCS Open Proof（PCS 开放证明）

在证明过程中，需要在特定的 challenge 值 r 处评估多项式 t。证明者需要计算多项式 t 的函数值 β = t(α)，并证明这个计算是诚实的（即，避免使用伪造的多项式）。

这个过程被称为 PCS 开放证明。commit 和开放证明是 PCS 中两个最关键的步骤。一般来说，commit 步骤很简单，而开放证明则更为复杂。

在 RISC0 V2 中，PCS 基于 Merkle 树（哈希）+ FRI（RS 码），而在 Varuna 中，PCS 基于 KZK10 MSM。在 Binius 中，PCS 基于 Merkle 树（哈希）+ Sumcheck + FRI（RS 码）。

值得注意的是，FRI 的使用在这两者之间存在显著差异。在 RISC0 中，FRI 用于低阶测试（与商多项式结合）以执行开放证明，而在 Binius 中，FRI 用于大域多项式的开放证明（稍后将讨论大和小域多项式）。此外，RS 码的构造也完全不同。

这是 Binius 的主要贡献。它的 PCS 基于 Merkle 树（哈希：Groestl256）、多变量sum-check（Multi-Variate Sumcheck）和 FRI（RS 码）。Merkle 树和哈希相对简单，而其他概念则更为复杂，如下所述。

RS Code（RS 码）

RS 码指的是一组码字，其中“码字”被定义为多项式 t 在集合 S 上评估的所有函数值的集合。计算多项式 t 的码字的过程称为编码，多项式 t 被称为消息。我们假设 t 是有限域 F 上的一个多项式。

例如，在 RISC0 中，多项式 t 的码字由其在 commitment 域上的所有函数值组成（也就是集合 S）。使用乘法 FFT 计算这些值要求 commitment 域形成一个阶数为 2 的幂的循环乘法群（在复数域中，FFT 是可行的，因为在复平面上的单位圆上存在任何阶数的循环乘法群）。由于所有计算都发生在有限域 F 中，因此要求 F 包含这样的乘法子群。

此外，对于 RS 码，码字长度，即 commitment 域 H 的大小，必须满足 |H| > deg⁡(t)+1 = trace length（迹长度），因为 RS 码是纠错码（信息中的错误可以很容易地被检测到，对应于可靠性），这需要引入冗余。

Additive NTT（加法数论变换）

定义如下：给定多项式 t 的系数：t_{0}, …, t_{2^l-1}，计算另一个单变量多项式 P 在超立方体 B_{l+R} 上的函数值。

其中，

• B_l 是加法子群（对应于 RISC0 中的迹域），
• B_{l+R} 是包含 B_l 的加法子群，对应于 R0 中的 commitment 域，尽管在实践中它是一个陪集，
• R 是 blowup 因子，在 R0 中为 2，在 Binius 中为 1，
• X_j(X) 是 F 上多项式向量空间的基函数，与标准基函数 1, X, X², … 完全不同。有关其严格定义，请参阅此链接。

MLE（多线性扩展）

Multi-Linear Extension（多线性扩展）：对于给定的函数 t:B_l → F，其多线性扩展是一个多项式函数 tilde_t(X_0,…,X_{l−1})，它满足：

• tilde_t 在每个变量 X_j 中都是线性的，即 tilde_t 关于任何变量 X_j 的阶数最多为 1，使得 tilde_t 是多线性的；
• tilde_t 在超立方体 B_l 上的函数值等于 t 的函数值，tilde_t 是 t 的一个扩展。

如公式（Eq. 2）所示，tilde_t 中的多项式 tilde_eq 正好是多变量多项式的拉格朗日基（其中由所有 l 变量的 MLE 形成的集合被视为一个 2^l 维的向量空间）。

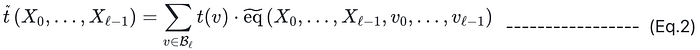
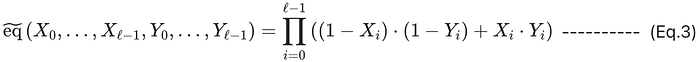
为什么使用 MLE？

在 RISC0 中，代数证明依赖于约束多项式和评估域上的消失多项式之间的可除性。然而，在二元域中，不存在乘法子群，并且消失多项式缺乏简单或有效的计算方法。

为了解决这个问题，Binius 采用了基于多变量多项式的零校验（Zero Check）来进行证明。零校验使用多变量多项式sum-check协议（Sumcheck protocol）来证明（我们将在后面介绍）。trace 被视为多变量多项式的最简单情况，即通过 MLE 获得的多线性多项式。

(为什么不使用来自 Varuna 的单变量多项式sum-check来进行证明？原因相同：缺少乘法子群。)

2. Binius PCS Commitment（Binius PCS 承诺）

Binius 中的所有计算都在二元域中执行，例如 F2 ~ F2⁷，这提供了高效计算和减少内存使用量的优点。

然而，为了在实现这些优势的同时遵守 Reed-Solomon (RS) 码的约束，出现了冲突。Binius 中多项式承诺方案 (PCS) 的设计主要是为了解决这些冲突。

• 冲突 1：在二元域塔中，不存在 2 的幂的乘法子群（由于拉格朗日定理），因此不能使用乘法 FFT。但是，二元域中存在加法子群，从而可以使用加法 NTT。
• 冲突 2：在多项式 t 的系数域（小域）中，没有足够大的子群来用作 RS 码的 commitment 域。RS 码要求 commitment 域大小 |H| > deg⁡(t)+1 = trace length（迹长度），但我们希望迹长度足够大（例如，段大小），同时保持 t 的内存使用量最小，即更喜欢小的系数域 F。此外，H 必须是有限域 F 的子集（因为所有编码计算都发生在 F 中）。例如，如果有限域 F2⁴ 且段大小或 |H| 为 2¹⁹，则 F2⁴ 的任何子集都不能用作 H，因为 |F2⁴| = 2¹⁶ < 2¹⁹。

对于冲突 2，一种简单的方法是将 t 的所有系数直接嵌入到更大的域中（例如 F2⁷），但这会增加内存使用量和计算开销（即，嵌入开销）。

Binius 通过使用 packing 技术来解决这个问题，其中 t 的多个相邻系数被打包到较大域中的单个元素中。例如，如果 F2⁴ 上的多项式 t 具有系数 [t0, t1,… ]，其中每个元素具有 16 位的位宽，则 Binius 将八个相邻元素打包到 F2⁷ 中的单个元素中，从而产生 F2⁷ 上的多项式 t′，如下图所示：

随后，使用 RScode 对 t′ 进行编码，t′ 是大域上的多项式，解决了冲突 2。然后，计算 t′ 的 Merkle 树根节点作为 commitment 值。Binius 中的 PCS 也被称为小域 PCS（small-field PCS）。

3. Ring-Switch（环切换）

如前所述，为了解决使用 RS 码时多项式 t 的系数域缺少足够大的 commitment 域的问题，Binius 引入 packing 技术。这涉及将 t 的相邻系数打包到较大域上的多项式 t′ 中，然后计算 t′ 的 Merkle 树根节点作为 commitment 值。

然而，这引入了另一个挑战：虽然 Merkle 树 commitment 是使用 t′ 建立的，但证明打开需要计算小域多项式 t 的函数值（未能解决这个问题可能会导致安全问题）。

为了解决这个问题，Binius 采用环切换（Ring-Switch）和 Sumcheck 将打开 t 的 commitment 的问题简化为打开 t′ 的 commitment 的问题，其中 t′ 的 commitment 开放证明通过 FRI 折叠和 Merkle 树查询来实现。

Binius 中的 PCS 也被称为小域 PCS。环切换的目的是将小域 PCS 的开放证明简化为大域 PCS 的开放证明，这有些复杂。我们尝试解释如下：

假设小域 MLE 是 t(X_0,…,X_{l−1})，并且在 packing 之后，生成的多项式是 t′(X_0,…,X_{l−κ})。我们需要证明 s = t(r_0,…,r_{l−1})，其中：

• r_j 是来自大域的随机 challenge 值（出于安全原因，随机 challenge 值通常从大域中提取，例如 F2⁷）；
• κ 是 packing 或扩展系数（extension coefficient）。例如，如果 t 的每个系数是 F2⁴ 的一个元素（位宽为 16 位），并且 t′ 的每个系数是 F2⁷ 的一个元素（位宽为 128 位），则 κ = log⁡2(128/16) = 3。

为方便起见，我们将 t 的系数域表示为 K，将 t 的系数域表示为 L，其中 L 是 K 的 2^κ 阶扩展。此外，L 是 K 上的 2^κ 维向量空间，具有基 β_0,…,β_{2^κ−1}。我们还将 l′=l−κl 表示为 l′=l−κl。

请注意我们的目标是证明（声明 1）：

3.1 如何证明（声明 1）？

请注意，通过将 r_0,…，r_{κ−1} 视为变量，并基于 MLE 的定义，我们可以推断：

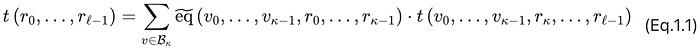
因此，我们得出结论，当且仅当（声明 2）成立时，（声明 1）成立：

这是因为，在（声明 2）的右侧，v_0,…,v_{κ−1} 遍历超立方体 B_κ。在接收到 hat_s_v 之后，验证者可以根据（Eq.1.1）轻松地计算 t(r_0,…,r_{l−1})，然后确定 s 是否等于 t(r_0,…,r_{l−1})。因此，问题简化为证明（声明 2）。

3.2 如何证明（声明 2）？

我们根据基 β_0,…,β_{2^κ−1} 展开所有 hat_s_v∈L，得到以下表达式：

此外，请注意，通过根据拉格朗日基展开多项式 t(v_0,…,v_{κ−1}, X_κ,…,X_{l−1}) 并在 r_κ,…,r_{l−1} 处对其进行评估，我们得到：

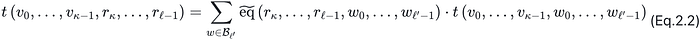
我们得出结论，当且仅当（声明 3）成立时，（声明 2）成立：

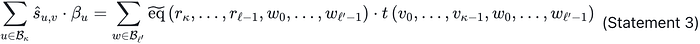
事实上，我们使用了两种方法来计算 hat_s_v：

• 在（声明 2）的左侧，hat_s_v 根据（Eq. 2.1）按 L 在 K 上的向量空间的基进行展开。
• 在（声明 2）的右侧，多项式根据拉格朗日基进行展开，然后进行评估，根据（Eq. 2.2）。

因此，问题简化为证明（声明 3）。

3.3 如何证明（声明 3）？

为了与 t′ 建立联系，因为我们的目标是将小域开放证明简化为大域开放证明，我们可以尝试用 β_v 表示 β_u 请注意 v 出现在（声明 3）中的 t 中，我们展开 hat_eq 多项式值的函数值：

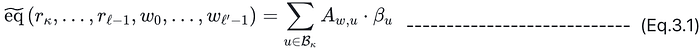
通过将（Eq. 3.1）代入（声明 3）并进行简化，并利用向量空间中基的线性独立性，我们得出结论，当且仅当（声明 4）成立时，（声明 3）成立：

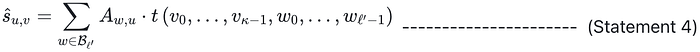
因此，问题简化为证明（声明 4）。

3.4 如何证明（声明 4）？

通过将两边乘以 β_v 并进行简化，我们得出结论，当且仅当（声明 5）成立时，（声明 4）成立：

其中 hat_s_u 定义为（Eq. 4.1）：

请注意，（Eq. 4.1）中的 u 来自（声明 4）的右侧，它起源于（Eq. 3.1），并且 hat_s_u 中的 u 必须与 A_{w,u} 中的 u 匹配。

因此，问题简化为证明（声明 5）。

3.5 如何证明（声明 5）？

由于（声明 5）是一个标准的 Multi Sumcheck 方程，因此可以使用 Multi Sumcheck 协议来证明。但是，我们的目标是证明（声明 5）对于所有 u∈B_κ 成立，将它们批量处理以减少证明的大小。为此，我们必须（声明 5）几乎等同于（声明 6）：

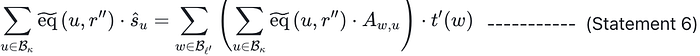
可以使用 Multi Sumcheck 证明（声明 6）。（为什么？在用（声明 6）两侧的 κ 变量替换 r′′ 之后，两侧都是 MLE。如果（声明 5）成立，则（声明 6）必须成立；如果两个 MLE 在随机选择的点处相等，则（声明 5）以极高的概率成立。）

3.6 总结：

要证明（声明 1）：

使用较少的 challenge 值，（声明 1）等价于（声明 2）：

通过使用两种不同的基扩展方法计算 hat_s_v，（声明 1）等价于（声明 3）：

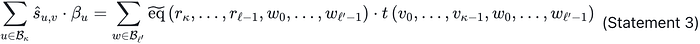
为了与 t′ 建立联系，消除 β_u，（声明 3）等价于（声明 4）：

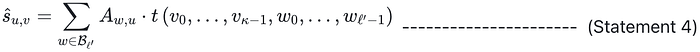
乘以 β_v 并简化，（声明 4）等价于（声明 5）：

批量进行 Sumcheck 证明，（声明 5）几乎等价于（声明 6）：

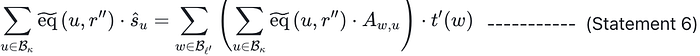
最后，我们定义了多项式 ( h )：

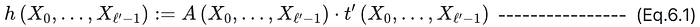
其中 A 由（Eq. 6.2）给出：

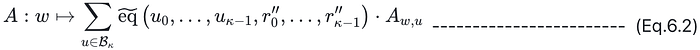
环切换的目的是计算多项式 h，（声明 6）s0 的左侧，用于后续的 Sumcheck 证明和 FRI。具体算法流程如下图所示：

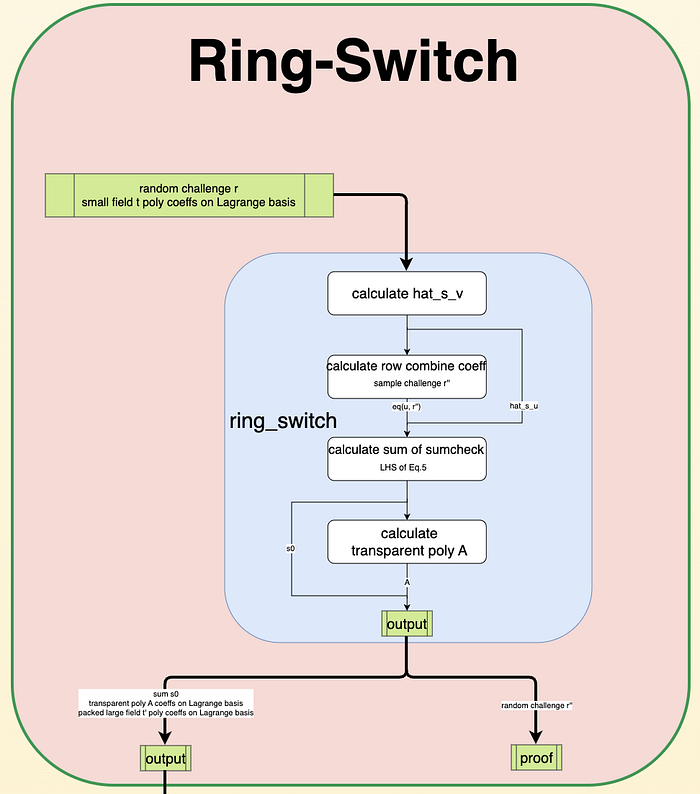
4. Sumcheck FRI

Sumcheck Protocol（sum-check协议）

Sumcheck 协议的目的是证明以下等式成立：

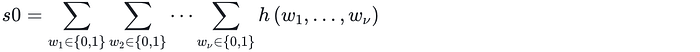
其中 h 的定义见（Eq. 6.1）。证明者需要证明这个等式成立，而不泄露 h 的系数。从上面的等式可以看出，右边实际上是多项式在“超立方体”所有顶点上的函数值之和，即 Sumcheck。

Prover（证明者）：

总共有 l’ 轮，证明过程如下：

对于 j=round_1, …, round_l′：

A. 证明者计算单变量多项式的系数：

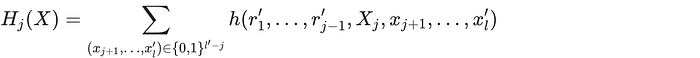
B. 证明者将 H_j 的系数附加到当前 transcript。

C. 证明者使用生成的 transcript 作为输入来生成随机挑战值 r′_j。

D. 证明者计算多变量多项式 h(r′_1,…,r′_j, X_{j+1},…,X_{l′}) 的系数。

Verifier（验证者）：

收到 transcript 后，验证者找到与 Sumcheck 对应的部分，并提取每个单变量多项式 H_j。

对于 j=round 1, …, round_l′：

验证者检查 H_j(0)+H_j(1) = H_{j−1}(r′_{j−1}) 是否成立。

— 如果对于所有 j 都成立，则验证者接受 Sumcheck 是正确的。

— 否则，验证者认为 Sumcheck 不正确。

此外，验证者检查 H_l′(r′_l′) == h(r′_1,…,r′_l′) 是否成立。

请注意，在最后一步中，验证者需要检查

H_l′(r′_l′) == h(r′_1,…,r′_l′) = A(r'_1, ..., r'_l') * t′(r'_1, ..., r'_l')。在这里，验证者可以独立计算 H_l′(r′_l′) 和 A(r′_1, …, r′_l′)（为什么？请参阅 Eq. 6.2 中的定义，其中涉及 hat_eq 多项式）。但是，t′(r′_1, …, r′_l′) 无法由验证者计算（为了确保零知识，验证者无权访问它）。

证明者使用 FRI 来计算和证明 t′(r′_1, …, r′_l′)。这是如何证明的？经过 FRI 折叠（FRI folding）后，t′ 的 RS 码变成了一个常数函数，这个常数正好是 t′(r′_1,…,r′_l′)（为什么？请参阅此链接）。此外，需要 Merkle 树路径证明来确保折叠过程是正确的。

具体算法流程如下图所示：

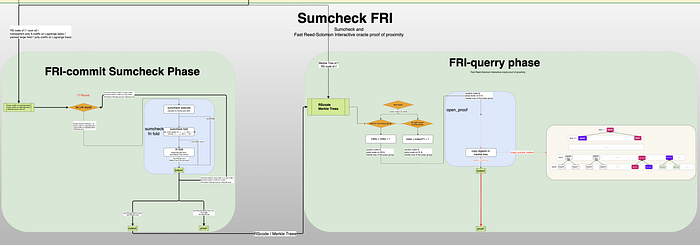
5. Conclusion（结论）

Binius 证明系统的 PCS 是一种复杂而创新的方案，它针对二元域进行了优化，从而在效率、安全性和实用性之间实现了平衡。通过使用加法 NTT、MLE 和环切换（Ring-Switch）等技术来解决二元域的局限性，Binius 为零知识证明提供了一个强大的框架，尤其是在计算资源有限的情况下。它的设计不仅提高了性能，而且为受限环境中的 ZK 证明系统树立了新的标准。特别是，它对 FPGA 或 ASIC 等硬件友好，因此可能会进一步加速。

• 原文链接： medium.com/@CFrontier_La...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～