Aleo 2025 年路线图及 Varuna 深入探索

TL;DR （太长不看）

最近，Aleo 发布了他们的2025 年路线图。我们分析了 Varuna 可能使用的算法来实现这一目标。

Varuna 是 Aleo 中 snarkVM 当前的证明系统，用于证明程序执行（用 Leo 语言编写）的正确性。它将证明一个或多个程序执行的正确性的问题简化为证明一个 R1CS 问题，底层证明利用了用于单变量多项式的 sum-check 协议。

1. 2025 年路线图

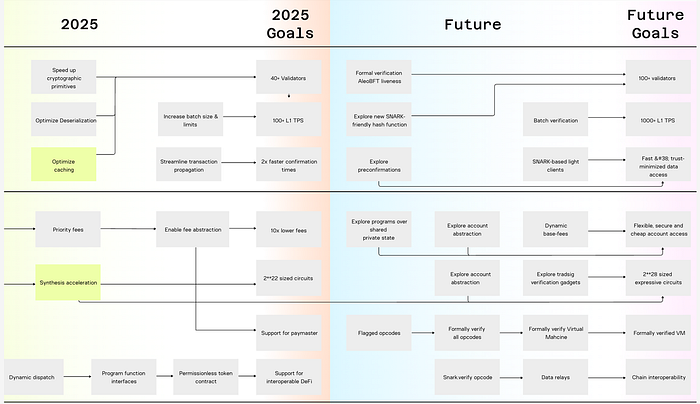
Aleo 正式发布了 2025 年路线图，如下图所示。2025 年的目标是支持大小为 2²² 的电路，并计划在未来支持大小为 2²⁸ 的电路，这对内存和计算能力提出了重大挑战。

为了实现这一目标，我们估计 Aleo VM 可能会朝着以下方向发展：

A. 支持递归功能，即将要证明的程序或电路拆分为多个部分，为每个部分单独生成证明，然后将这些证明聚合为最终证明。

B. 开发更有效的多项式承诺方案。

C. 目前，Varuna 使用 BN254 的基域，其中每个元素占用大量内存，并且该域中的算术运算需要大量的计算。切换到更小的域可以显著减少内存使用和计算需求。

来源：https://aleo.org/roadmap/

另请参阅我们之前的文章，通往 Aleo 的通用 ZKVM 之旅 和 高级 ZK 硬件加速：Aleo ASIC 矿机背后的技术。

2. 简介

Varuna 算法主要由三个部分组成：电路综合、代数全息证明和多项式承诺方案。我们将详细介绍和分析 Varuna ZKP 算法的代数全息证明部分（即，如何通过多项式表示和计算来证明约束），这是 Varuna 中最具挑战性的部分。

本文将从理论角度分析和介绍该算法的原理，提供一个简单的数学推理过程，并结合 Aleo 2025 年路线图讨论 Varuna 的未来发展。

如下图所示，本文将重点关注图表的左侧部分，即代数全息证明（其中“全息”指的是证明过程所需的少量查询）。电路综合和多项式承诺方案虽然在逻辑上有些复杂，但与其他证明系统中的类似。

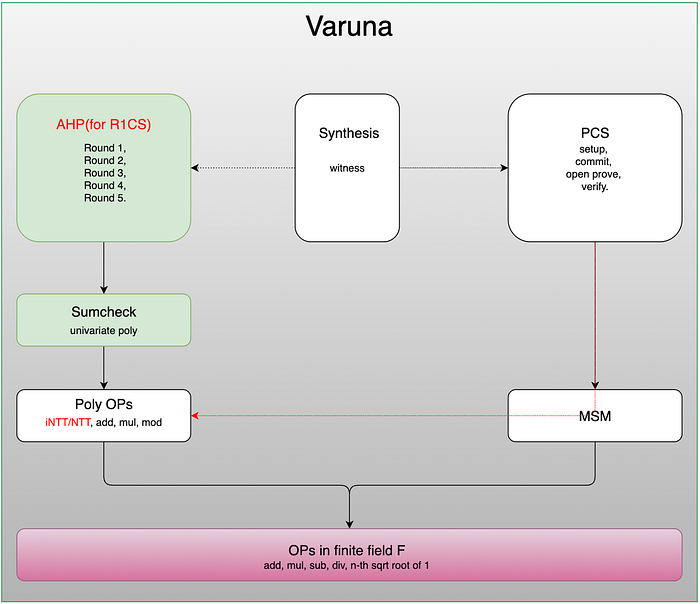
以下文字将解释 Varuna 证明的问题，提供所用术语的严格定义，然后详细分析为解决此问题而引入的五个轮次（其中第 3 轮和第 4 轮更为复杂，而其他轮次则更简单）。由于篇幅限制，对于所涉及的数学基础，我们将仅简要解释概念和定理，而不提供详细的描述或证明，并鼓励读者参考他们感兴趣的任何抽象代数教材。

3. R1CS 问题和定义

Varuna 算法的目的是证明程序（用 Leo 语言编写，假设目前只有一个程序；稍后将讨论证明多个程序的过程）的执行是正确的。为了实现这一点，Varuna 首先执行程序，并根据执行期间的计算类型和中间结果，构造三个矩阵 A、B、C 和一个向量 z。这使得证明程序执行的正确性的问题简化为证明这三个矩阵和向量 z 满足某些约束。我们提供以下定义：

定义 3.1：R1CS 问题

对于给定的矩阵 A、B、C 和向量 z，R1CS（Rank-1 Constraint System，秩 1 约束系统）指的是证明以下等式成立：

• 矩阵 A：有限域 F 上的一个 (m, n) 维矩阵（即，矩阵的元素属于 F，而不是实数）。有限域是一个可以执行四种基本算术运算（加法、减法、乘法和除法）的集合，并且集合中元素的数量是有限的（有关严格的定义，请参阅教材）。
• 矩阵 B、C：与 A 的定义类似，但作为不同的矩阵，所有三个矩阵都具有相同的维度。
• z：有限域中的一个 n 维列向量，其中 z 包括程序的公共输入和见证（即，公共输入和程序执行的中间结果），例如 z = (x, w)。
• Az：表示标准的矩阵向量乘法，得到一个列向量 a_z。类似地，定义 b_z 和 c_z。
• Az 和 Bz 的乘积：表示列向量之间的 Hadamard 积，即，两个向量中对应元素的逐元素乘法。

如下图中的简单示例所示，这说明了如何将指令的算术运算转换为 R1CS 问题。请注意，矩阵的每一行对应一个约束，并且当且仅当相应指令的计算正确时，约束才成立。

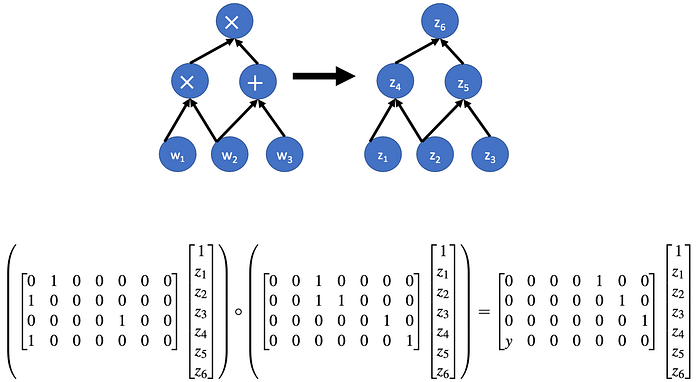
来源：Justin Thaler 的 Proofs, Arguments and Zero Knowledge

引理 3.2：Sum-check（sum-check）

对于有限域 F 上的给定多项式 f(Y)（即，多项式的系数属于 F），如果且仅当存在 F 上的多项式 h(Y) 和 g(Y) 使得以下等式成立时，f 在 F 中的循环群 C（一个非零乘法子群，与 R1CS 中的 C 略有滥用符号，但很容易区分）上的和等于 σ：

• σ：F 中的一个元素。
• C：由 F 中所有非零元素在乘法下形成的乘法群的子群。群，是一个定义了“乘法”运算的集合。值得注意的是，有限域中的任何乘法子群都是循环群，这意味着群中的每个元素都是某个元素的整数幂。这一点至关重要，因为零知识证明中的许多算法（尤其是 Varuna）都依赖于循环群的简单结构。
• |C|：循环群 C 中元素的数量。由于 F 是有限的，因此 C 必然是有限的。
• vC(Y)：循环群 C 上的 vanishing polynomial （零化多项式），即，在 C 的每个元素处求值为零的多项式。可以类似地定义循环群上的其他 vanishing polynomial。

为了便于在以下章节中进行讨论，我们假设 R1CS 中三个矩阵的行索引（例如 A 中的行索引）被视为从 F 的循环子群 R 到 F 的函数。我们将此循环子群 R 称为约束域（即代码中的 constraint_domain）。与列索引对应的循环子群 C 称为变量域（即代码中的 variable_domain）。根据上下文，很容易区分 C 是指 R1CS 中的矩阵还是指变量域，从而避免符号混淆。

显然，z 应被视为从 R 到 F 的函数，并且要证明的程序的公共输入（即代码中的 public_input）被视为 R 的子群 H0 上的函数，我们称之为输入域（即代码中的 input_domain）。

此外，如上面的 R1CS 示例所示，三个矩阵中的许多元素为零。为了节省内存和计算，每个矩阵中的所有非零元素都按照其出现的顺序进行排序，并且与此排序的索引对应的子群 K 称为非零参数域（即代码中的 nonzero_domain）。

4. 第 1 轮：生成见证偏移多项式和随机多项式

4.1. 计算见证偏移多项式

计算以下多项式：

• x：要证明的程序的公共输入。
• H0：输入域，其元素数量是大于或等于公共输入中元素数量的最小 2 的幂。
• vH0(X)：H0 上的 vanishing polynomial。
• hat_x(X)：公共输入 x 的低次扩展多项式，通过 IFFT 获取 x 在 H0 上的函数值。
• z’(X)：函数 z’ 的低次扩展多项式，其中 z’ 表示公共输入和 witness。

4.2. 生成随机掩码多项式

生成过程相对简单，如下式所示：

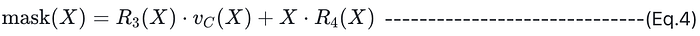
• R3(X), R4(X)：系数为 F 中的随机元素的多项式，其中 R3(X) 的次数为 3，R4(X) 的次数为 4。
• vC(X)：C 上的 vanishing polynomial（在代码中，这对应于最大变量域）。

为什么需要掩码多项式？

它在第 3 轮中用于实现零知识属性。

4.3. 证明过程

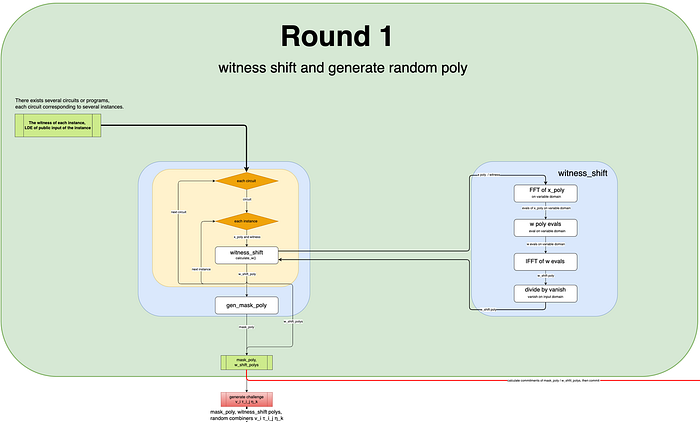
下图说明了第 1 轮的计算过程。请注意，该图涉及迭代电路以及每个电路的多个实例。这是因为 Varuna 支持所谓的批量证明，其中多个电路及其各自的多个执行被一起证明，从而只生成一个证明。

5. 第 2 轮，行检查

5.1 证明原理

目标是证明以下内容：

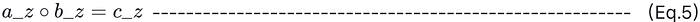
• a_z = Az，矩阵 A 和列向量 z = (x, w) 的乘积，b_z 和 c_z 的定义类似
• 左侧的乘法是逐元素乘法，而不是向量内积。
• 要证明的等式由 m 个等式组成，对应于 m 个约束。如果程序执行正确，则这些 m 个等式成立。

如何证明？ 这很简单。

1. 使用 IFFT 计算 a_z、b_z 和 c_z 的低次扩展多项式，得到 hat_az(X)、hat_bz(X) 和 hat_cz(X)。

2. (Eq. 5) 成立，这意味着 R1CS 中的每个约束都得到满足，当且仅当对于 R 中的任何元素 x，x 是等式 hat_az(X)·hat_bz(X) — hat_cz(X) = 0 的根。

3. 步骤 2 中的语句成立当且仅当 R 上的 vanishing polynomial v_R(V) 可以整除 hat_az(X)·hat_bz(X) — hat_cz(X)。也就是说，存在 F 上的多项式 h0(X) 使得：

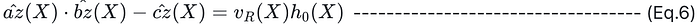
4. (Eq. 6) 成立几乎等同于以下等式成立，其中 α∈F\R 是一个来自 F 中的随机挑战值：

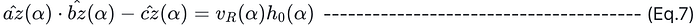
5. 第 2 轮的目的是计算 h0(X)，计算其承诺值并提交。

6. 当验证者收到用于验证的证明时，他们需要检查 (Eq. 7) 是否成立。

5.2 证明过程

第 2 轮的特定证明过程如下图所示：

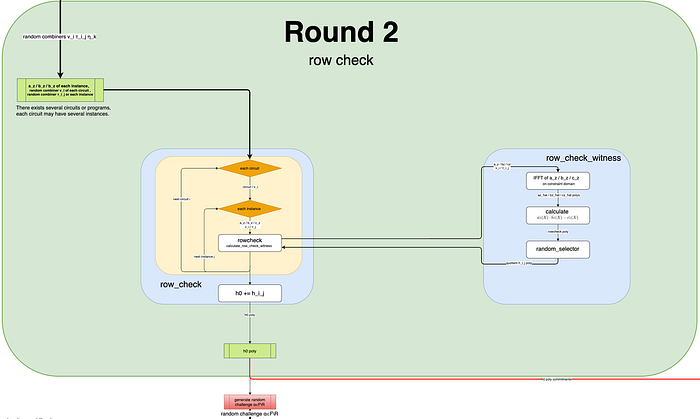
请注意，在第 2 轮中，该过程会迭代多个电路以及每个电路的多个实例，从而计算 row_check_witness。

Varuna 最重要的特性是对批量证明的支持，其中包括一起证明多个电路及其多个实例，从而生成单个证明。

由于有多个电路，每个电路都可能具有多个实例，因此一种简单的实现方式是需要为每个电路的每个实例计算 h0(X) 多项式，计算其承诺值并提交。但是，这种方法会导致提交许多承诺值，从而导致证明大小很大。

相反，我们的目标是将来自多个电路和实例的所有商多项式组合成一个多项式并提交其承诺值。这是通过计算以下表达式来实现的，该表达式是通过简单的数学推理得出的。

• R：最大的约束域。
• Ri：第 i 个电路的约束域。
• vRi(X)：之上的 vanishing polynomial。

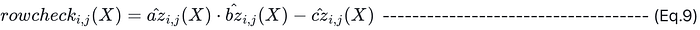
6. 第 3 轮，线性检查

6.1 证明原理

线性检查是计算并证明矩阵向量乘法是正确的，即计算并证明以下等式成立：

• M ∈ {A, B, C}，其中 a_z 表示矩阵 A 和向量 z = (x, w) 的乘积，b_z 和 c_z 的定义类似。

为什么有这个必要？

1. R1CS 本身需要证明这个等式。

2. 在第二轮的验证过程中，验证者需要计算：

但是，验证者无法直接计算，因为他们没有 M（可能非常大）或 z。因此，他们依赖于证明者。

请注意，(Eq. 11) 成立几乎等同于 (Eq. 10) 成立，因此我们只需要计算并证明 (Eq. 11)。

如何证明？

为了便于解释，我们首先假设只有一个电路。对证明过程的直观理解如下：

1. 利用循环群 ( C ) 上的单变量多项式的sum-check协议。 Sum-check 引理：如定义 3.2 中所述，对于多项式 ( f(Y) )，如果且仅当存在多项式 h(Y) 和 g(Y) 使得：

2. 请注意，矩阵向量乘法本质上是一个求和。

3. 证明的关键是计算 f(Y) = hatM(α, Y) · z(Y)，其中 hatM(α, Y) 是 M 作为二元多项式的低次扩展。

4. 为了计算 f(Y)，考虑 hatM(X, Y) 的 Lagrange 基展开：

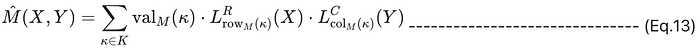
• R：约束域，即 M 的行索引的域。
• C：变量域，即 M 的列索引的域。
• K：与通过按出现顺序对矩阵 M 的所有非零元素进行排序而获得的索引相对应的循环子群，即代码中的非零域。
• valM(κ)：将 M 的所有非零元素视为 K 上的函数，hat_valM(Z) 作为其低次扩展多项式。
• rowM(κ)：将 M 的所有非零元素的行索引视为 K 上的函数，hat_rowM(Z) 作为其低次扩展多项式。
• colM(κ)：与 rowM(κ) 的定义类似。
• L_rowM(κ)_R(X)：与 R 上的第 rowM(κ) 个元素相对应的 Lagrange 基函数，L_colM(κ)_C(Y) 也是如此

5. 使用 M 的低次扩展 (Eq.13)，我们可以轻松构造 f(Y)。

6. 然后，应用sum-check引理，(Eq. 11) 成立几乎等同于以下等式成立，其中 β 是 F\C 中的随机挑战值：

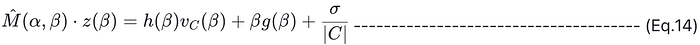
7. 第 3 轮的目的是计算 h(Y) 和 g(Y)，提交它们，并确保零知识属性。

8. 验证者在验证期间需要检查 (Eq. 14) 是否成立。

6.2 证明过程

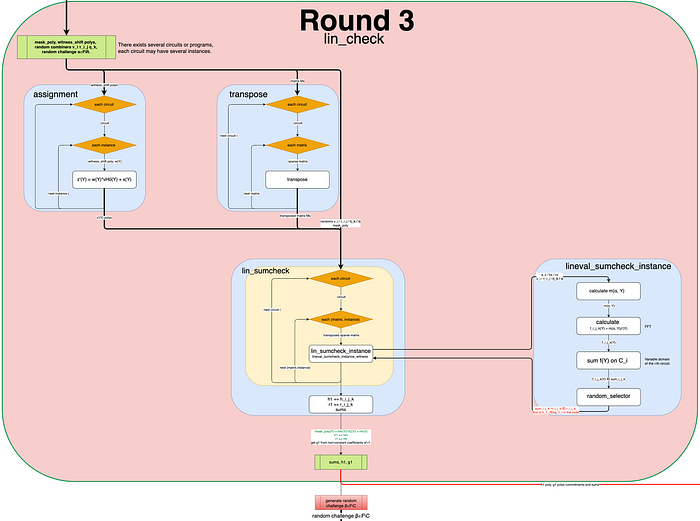
此外，请注意，在第 3 轮中，该过程会迭代多个电路以及每个电路的多个实例。与第 2 轮中的证明过程类似，对于多个电路和实例，我们的目标是将所有商多项式 h(Y) 和余数多项式 r(Y) 组合成一个多项式，即计算以下等式中的 h1(Y) 和 r1(Y) 并提交它们的承诺值：

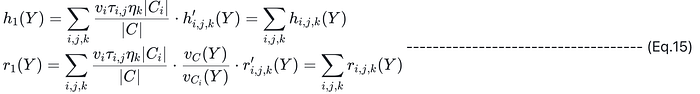
• C：最大的变量域。
• Ci：第 i 个电路的变量域。
• vC(Y)：C 上的 vanishing polynomial。
• h’_ijk(Y) 和 r’_ijk(Y) 必须满足以下等式：

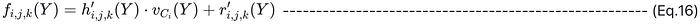
7. 第 4 轮，有理检查

7.1 证明原理

计算并证明二元矩阵多项式的求值

• M ∈ {A, B, C}。
• hatM(X, Y)：M 的低次扩展多项式，如 (Eq. 13) 中所述。
• α：来自 F\R 的随机挑战值。
• β：来自 F\C 的随机挑战值。

为什么有这个必要？

1. 在第 3 轮中，验证者需要计算 hatM(α, β) 以进行最终检查，但无法直接这样做（由于计算成本高昂）。因此，证明者必须计算并证明它。

2. 直接使用从矩阵的 Lagrange 扩展获得的二元多项式进行证明的计算成本很高。因此，引入了导数多项式基。以下是 Lagrange 基函数展开式和导数多项式基函数展开式：

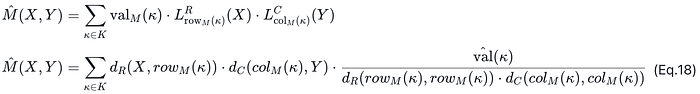
• dR(X, Y) = [vR(X) — vR(Y)] / (X — Y)。
• R：约束域。
• C：变量域。
• K：非零参数域。

如何证明 (Eq. 17)？

为了便于解释，我们首先假设只有一个电路。

1. 使用商多项式的定义，简化 (Eq. 18)，获得以下表达式：

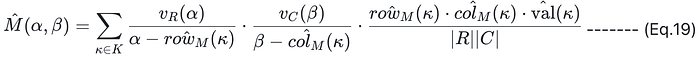
2. 定义以下多项式 r(Z)：

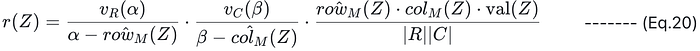
然后，(Eq. 17) 成立当且仅当有理多项式 r(Z) 在 K 上的和等于 ω。

3. 步骤 2 中的语句成立当且仅当存在多项式 h4(Z) 和 gM(Z) 使得以下等式成立：

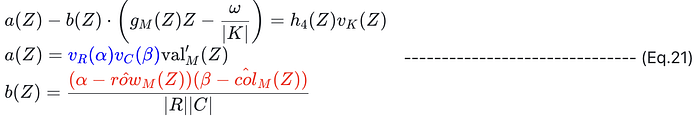
4. 第 4 轮的目的是从以上等式中计算 ω、hM(Z)、gM(Z)、a(Z)、b(Z) 并提交它们（对于多项式，计算其承诺）。

7.2 证明过程

基于以上描述，我们可以获得第 4 轮的证明过程，如下图所示：

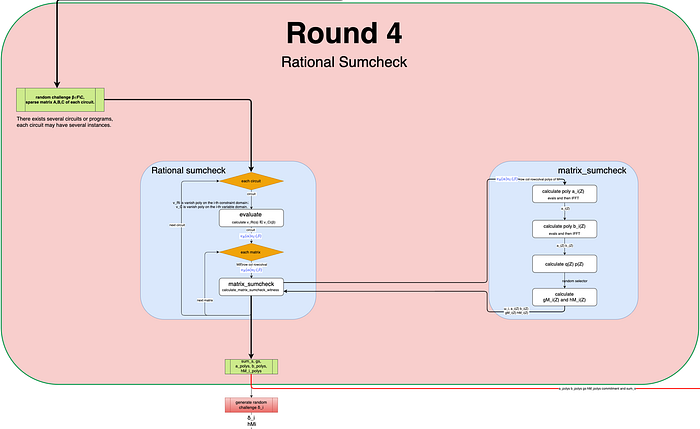
与第 2 轮和第 3 轮中的方法类似，所有 hM_i(Z) 多项式都组合在一起（使用随机选择，但是组合器稍后获得并在第 5 轮中累积）。

8. 第 5 轮

第 5 轮的过程相对简单，只需要完成以下计算即可：

9. 总结

总之，Varuna 的代数全息部分的证明过程主要包括以下五个轮次：

第 1 轮：证明的准备工作，生成 witness_shift 多项式和随机多项式 mask(X)，用于实现零知识 ZK。

第 2 轮：行检查，证明 R1CS 中的每个行约束都成立。

第 3 轮：线性检查，计算并证明矩阵向量乘法是正确的，同时还支持第 2 轮。

第 4 轮：有理检查，支持第 3 轮，计算并证明矩阵 M 的低次扩展多项式在 (α, β) 处的求值：ω = hatM(α, β)。

第 5 轮：随机组合来自第 4 轮的商多项式并计算其承诺值，支持第 4 轮。

• 原文链接： medium.com/@CFrontier_La...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～