有限域算术优化

TLDR

有限域算术运算在 ZKP 证明系统中至关重要，我们介绍了一些简单新颖的域计算算法，至少提高了扩展域 K 中乘法的 20% 性能，以及基础域 F 中从整数到 Montgomery 表示的 Montgomery 变换的 30% 性能。

1. 目标

在许多零知识证明系统（例如 SP1 和 RISC0）中，大多数计算发生在有限域内，包括有限域加法、乘法和除法。 因此，高效的有限域算术运算对于零知识证明系统的性能至关重要。 我们将介绍一些新颖的有限域计算算法，并提供性能比较数据。

2. 有限域

域 是一个集合 F，配备了两种运算，分别称为“加法”和“乘法”，分别表示为 + 和 ⋅，并且满足以下条件：

A. F 在加法下形成一个 阿贝尔群：

• 存在一个加法单位元素 0∈ F。
• F 中的每个元素都有一个加法逆元。
• 加法是结合律和交换律。

B. F ∖{0} 在乘法下形成一个 阿贝尔群：

• 存在一个乘法单位元素 1∈ F ∖{0}。
• F 中每个非零元素都有一个乘法逆元。
• 乘法是结合律和交换律。

例如，实数集 R 在标准加法和乘法下，构成了实数域 R。如果一个域 F 包含有限数量的元素，则称它为 有限域。

一个 素域 F p 定义为集合 F p ={0,1,2,…, p −1}，其中 p 是一个素数。 它的运算是：

• 加法：a + b =( a + b) mod p (其中第二个“+”表示整数加法，而 mod 是模运算)。
• 乘法：a ⋅ b =( a × b) mod p (其中 × 表示整数乘法)。

域 F 的一个 域扩张 K 是指一个域，使得 F 是 K 的一个子域（即，F ⊆ K，并且 K 的运算，当限制在 F 上时，满足域的公理）。 例如，复数 C 构成了实数 R 的一个扩张域。

由于素域 F p 在零知识证明系统中被广泛使用，我们专注于 F p 及其扩张域 K 中的计算。 不失一般性，我们假设：

很容易知道多项式 X 4+11 在 F[X] 中是不可约的，那么商环 F[ X]/( _X^_4+11) 构成一个域，并且是 F 的扩张。

3. 域 F 及其扩张域 K 中的运算

域 F 中的运算通常包括加法、减法、乘法和求逆，其中加法和乘法是在域 F 中定义的基本运算，而减法和求逆可以由这些基本运算构造出来。 类似地，扩张域 K 中的运算可以从 F 中的运算导出，因此我们首先关注 F 中的加法和乘法。

基于素域的定义，F 中的加法定义为 a+b = (a+b) mod p。 注意 0≤a≤p−1, 0≤b≤p−1。 当 a+b 作为整数加法计算时，结果 c=a+b 满足 0≤c≤2p−2。 因此 c mod p 可以计算为：c mod p = if c<p then c ; 否则 c−p。 这意味着 F 中的加法可以很容易地通过 1~2 个整数加法/减法运算和一个逻辑比较来计算。

F 中的乘法定义为 a⋅b=(a⋅b) mod p。 注意 0≤a⋅b≤(p−1)^2。 当 a⋅b 很大时，需要大量的减法运算才能将 a⋅b 简化为域 F 中的一个元素。或者，可以使用一个除法，例如 q = ⌊(a⋅b)/p⌋, 并且 (a⋅b) mod p = (a⋅b)−(p⋅q)。 然而，除法运算在硬件或 GPU 实现中需要大量的周期。 为了解决这个问题，我们引入 Montgomery 约简。

4. Montgomery 约简

为了在不使用除法的情况下将给定的一个大整数约到 [0, p) 范围内，Montgomery 约简基于以下公式：

该公式显然成立，因为，通过考虑表达式 z + ((z⋅p′ mod R)⋅p) 中的运算作为环 Z/RZ 中的乘法和加法，存在一个整数 k 使得以下关系得到满足：

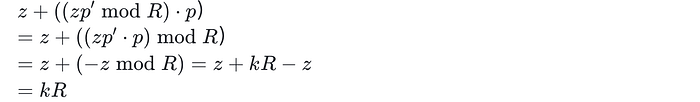
也就是说，公式 (1) 中的分子是 ( R ) 的倍数。

此外，请注意 Rc = R(z⋅R_inv mod p)。 通过将乘法视为域 F 中的运算，我们有：

对于 x∈[0,p)，假设 tilde_x = xR mod p， y 和 tilde_y 的定义类似。 根据域 F 的定义，以下公式成立：

从公式 (2) 可以看出，我们可以使用公式 (1) 即 Montgomery 约简进行 tilde_x 和 tilde_y 的乘积计算。 然而，这需要首先将 x 转换成 tilde_x = xR mod p，这个计算代价很高。 这种转换可以通过例如 Mont(x,R2) 来实现，其中 R2=(R⋅R) mod p, 并且 R2 可以预先计算。在许多证明系统中，这种转换通常只需要执行一次，然后进行大量的乘法或除法运算。 因此，Montgomery 乘法是一种有效的元素相乘的方法。

此后，我们将此转换称为 Montgomery 变换，而 tilde_x 称为其 Montgomery 表示。

5. 优化后的 Barrett 约简

在许多证明系统(如 SP1 和 RISC0)中，当生成一个 trace 时，需要使用 Montgomery 变换将 [0, 0xffffffff) 范围内的许多整数转换为 Montgomery 表示。 然而，Montgomery 变换的计算成本相对较高。 为了解决这个问题，可以引入 Barrett 约简，如下式所示：

公式 (5) 的正确性或 Barrett 约简的正确性证明可以在参考文献 [1] 的 Note 2.15 中找到。 只要注意到，从这个证明中，可以表明：0≤(z−hat_q⋅p) < 3p。

然而，请注意，由于 μ>(1≪32)，需要一个 u64 来表示 μ。 此外，由于 0≤⌊z / b^(k−1)⌋< (1≪34)，它也需要一个 u64 来表示。 这导致一个 u64-u64 乘法和一个 u64-u32 乘法，计算成本很高。 为了解决这个问题，我们可以利用 μ 和 p 的属性来简化计算。

此外，Montgomery 变换是 tilde_x = xR mod p, 那么令

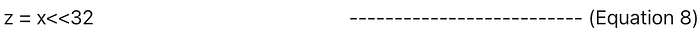
使用公式 6 ~ 公式 8， 我们可以将公式 3 和公式 4 更改为以下形式：

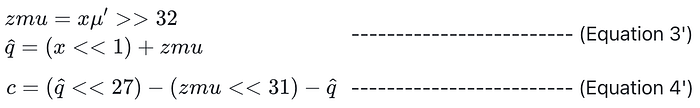
那么，优化后的 Barrett 约简只需要一个 u32 乘法，以及其他的移位、加法和减法，这些都比乘法运算更有效。

6. 扩张域 K 中的乘法

我们知道，扩张域 K 中的元素本质上是一组多项式 { r(X)+q(X)p(X) | q(X)∈F[X] }，其中 p(X) 是一个不可约多项式，例如上面定义的 p(X)=X^4 + 11，其中 r(X)∈F[X] 且其次数小于 4。

因此，K 中的元素可以通过其相应的多项式 r(X) 表示，该多项式可以使用来自域 F 的 4 个元素表示为多项式的系数。

扩张域 K 中的乘法运算包括多项式乘法，然后是关于 p(X) 的多项式约简：

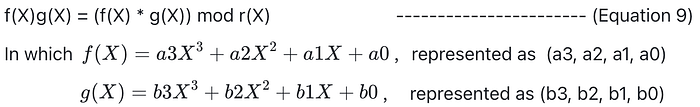
那么 h(X) = (f(X) ⋅ g(X)) mod r(X) 的系数：

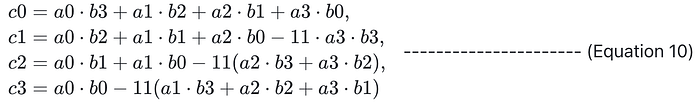
从公式 (10) 可以看出，扩张域 K 中的乘法是通过域 F 中元素的乘法和加法来实现的。 值得注意的是，这主要涉及向量的内积，例如计算 inn3=a0⋅b2+a1⋅b1+a2⋅b2。 如果使用域 F 中的乘法和加法运算进行朴素计算，则需要多次 Montgomery 约简（例如，inn3 需要 3 次约简），每次约简都涉及大量的计算成本：

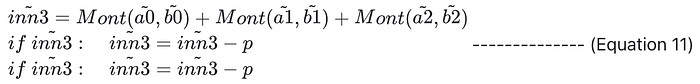
假设我们已经使用优化的 Barrett 约简对 a0 执行了 Montgomery 变换，即 tilde_a0 = a0⋅R mod p，同样对于 tilde_a1, tilde_a2, tilde_b0, tilde_b1, tilde_b2 也是如此。 那么 tilde_inn3 是：

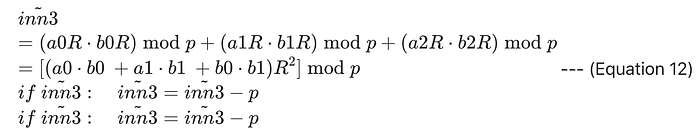
从公式 (12) 可以看出，我们只需要执行一次 Montgomery 约简，这大大提高了内积的计算性能。 因此，可以优化扩张域 K 中的乘法运算。

7. 性能比较

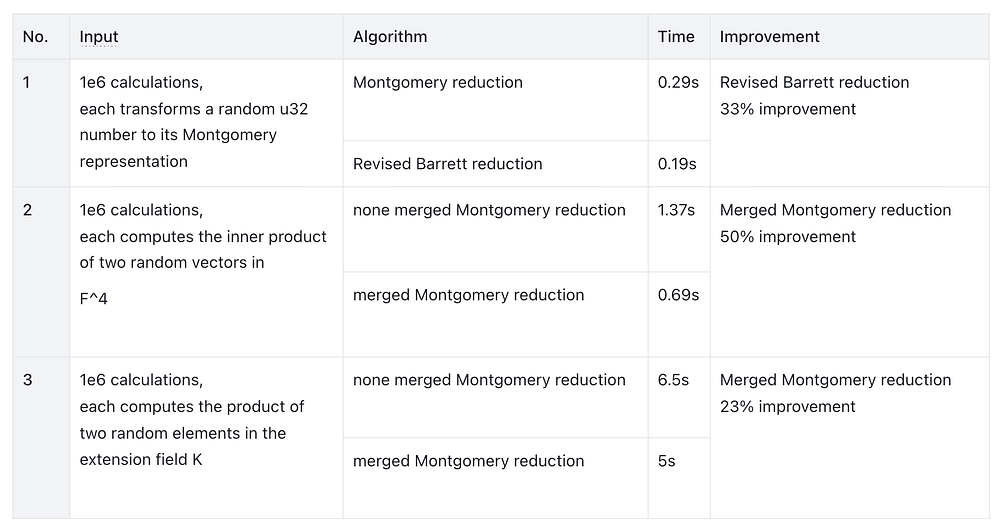
我们用 Python 实现了以下三种简单算法，并收集了性能数据：

1. 用于 Montgomery 变换的优化 Barrett 约简；
2. 在两个向量的内积计算中合并 Montgomery 约简。
3. 用于扩张域 K 中乘法的合并 Montgomery 约简；

测试平台：Mac M3, 16GB RAM, Python 实现。

8. 参考文献

1. Menezes, A. J., Vanstone, S. A., & Oorschot, P. C. V. (2004). Guide to elliptic curve cryptography. Springer.

• 原文链接： medium.com/@CFrontier_La...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～