基于哈希证明系统的区块链两方椭圆曲线签名
- 刘峰老师
- 发布于 2022-02-14 15:14
- 阅读 6517
椭圆曲线数字签名算法(ECDSA)是区块链密码学技术中常见的数字签名之一,其在加密货币、密钥身份认证等方面已被广泛应用。然而当前的区块链ECDSA算法灵活性较低、匿名性较弱且分散性不高,性能相对高效的应用实例也十分有限。基于哈希证明系统,文章提出一种适用于区块链的两方椭圆曲线数字签名算法。通过给定签名算法的数理逻辑及其安全模型,融入区块链进行测评,证明了方案的可行性。最后,对签名方案的安全性进行了分析,证实该方案无需交互性安全假设便可在零知识性的基础上减少通信开销。
摘 要 :椭圆曲线签名ECDSA是区块链密码学技术中常见的数字签名之一,其在加密货币、密钥身份认证等方面已被广泛应用。然而当前的区块链ECDSA算法灵活性较低、匿名性较弱且分散性不高,性能相对高效的应用实例也十分有限。故拟借助哈希证明系统,提出一种适用于区块链的两方椭圆曲线签名。通过给定签名算法的数理逻辑及其安全模型,融入区块链进行测评,证明了方案的可行性。最后,对签名方案的安全性进行了分析,利用基于模拟的安全证明方式证实出该方案无需交互性安全假设,便可在具备零知识性的基础上减少通信上的开销。
关键词:哈希证明系统; 椭圆曲线签名;区块链;安全性证明;隐私保护
Two-Party ECDSA for Blockchain Based on Hash Proof Systems
Abstract: Elliptic curve signature ECDSA is one of the common digital signatures in blockchain cryptography technology, which has been widely used in cryptocurrency, key identity authentication, etc. However, current blockchain ECDSA algorithm is inflexible, weakly anonymous and poorly decentralized, and have limited examples of relatively high-performing applications. This study intended to propose a two-party elliptic curve signature suitable for blockchain with the help of hash proof systems. Given the mathematical logic of the signature algorithm and its security model, its incorporation into the blockchain was evaluated to show the feasibility of the scheme. Finally, the security of the signature scheme was analyzed, and a simulation-based security proof was used to demonstrated that the scheme did not require interactive security assumptions and can reduce the overhead in communication with zero knowledge proof.
Key words: Hash Proof System; ECDSA; Blockchain; Security Proof; Privacy Protection
0 引言
椭圆曲线数字签名算法源自于1985年KOBLITZ^ [1]^ 与MILLER^ [2]^ 提出的椭圆曲线公钥密码体制(ECC),是一种安全性基于解离散对数问题困难的数字签名算法。在现代密码学的非对称加密中,RSA、ElGamal等公钥密码体制需要1024 bit长度密钥才能实现80位的安全级别^[3,4]^ ,而椭圆曲线签名算法在私钥长度为160 bit时就可实现80位的安全级别。简言之,椭圆曲线数字签名算法能以短密钥实现高安全,也正是如此,ECDSA在区块链这种分布式系统发展早期被广泛地采纳为默认签名算法。
在比特币诞生之初,区块链上的ECDSA算法多数是基于SECP256K1曲线的构造,该曲线因具备自同态映射的特性可加速消息验签过程曾备受青睐。不过随着工程应用的更迭,基于这种曲线的签名算法也暴露出诸多缺点,如总体算法结构冗杂、易遭受侧信道攻击与信息隐私性差等^[5,6]^ 。虽然有学者尝试性设计了基于Montgomery曲线的ECDSA高效算法,并且对其中的标量乘步骤实施了优化以进一步提升签名效率^[7]^ ,但此类改进依然无法抵抗有效代数故障注入这种侧信道攻击,量子威胁也对ECDSA算法带来了很大的冲击^[8]^ 。此外,当前大多数ECDSA算法因随机预言机产生的哈希函数与椭圆曲线中存在的离散对数困难问题,安全性也不利于有效证明^[9]^ 。
随着多方计算的场景逐渐增多,多方协作签名的需求也迫使ECDSA算法寻求改进,基于门限签名机制(Threshold Signature Scheme,TSS)的ECDSA算法便是改进过程中一个探讨的方向,这在当前的去中心化跨链技术方案中也是一个炙手可热的研究点。LINDELL^[10]^ 在2017年提出了一种快速安全两方ECDSA签名方案,深入分析了ECDSA门限签名协议在博弈安全证明下的安全性与相关假设下的应用方式。然而这种产生ECDSA签名的门限技术方案需要依赖繁重的密码学原语假设,这对原本ECDSA签名的性能影响很大,实际应用的效益也大大减弱。DOERNER ^[11]^ 等人发现LINDELL方案这一缺陷,基于计算Diffie-Hellman假设以及ECDSA自身依赖的原语假设提出了一个可在随机预言机中抵抗恶意敌手攻击的新型安全两方门限ECDSA签名方案,此方案在密钥生成和签名效率上有很大的提升。在此之后,LINDELL^[12]^ 等人分析出此签名方案虽然在签名效率上有所提升,但却不可避免地带来了严重的带宽问题,且并没有具体展示多方设置的方法,进而他们提出了可分散密钥生成与签名的多方ECDSA的门限签名协议。不过,这种协议方案的消息隐私处理方面尚需改善。CASTAGNOS^[9]^ 等人则在2019年的论文中基于Lin的方案设计出无需交互性假设的基于哈希证明系统的两方ECDSA签名方案,且基于模拟安全情况下给出方案是紧安全性规约的结果证明。
本文研究将以CASTAGNOS^[9]^ 等人提出椭圆曲线数字签名方案为基准,提出能够融入区块链的基于哈希证明系统的两方椭圆曲线签名方案。通过设定合理的计算模型来进行模拟安全分析,拟定在区块链上构造合理的验证操作完善签名方案,使得基于模拟的安全简洁构造方案在真实场景中同样适用且具备灵活性与可分散性。该方案也通过较少的传输比特信息的轮换次数,无需交互性假设即可实现隐私信息的零知识性,实现较为安全的数字签名技术。
1 相关知识
1.1 符号定义
在介绍相关的基础知识与签名算法前,预先给出一些通用符号的定义与简要说明以便于理解,如表1所示。
表1 通用符号定义与说明
| 符号标记 | 解释说明 |
|---|---|
| XX | NP问题的一个实例集合 |
| LL | 归属XX的NP语言集合 |
| WW | 证明给定元素在LL内的证据集合 |
| RR | 定义语言LL的二元关系,R**⊂X×**WR⊂X×W |
| Z**q**Zq | 整数模qq的乘法群 |
| Z**∗**qZq∗ | 单位群 |
| R**D**LRDL | 椭圆曲线离散对数知识的功能性函数 |
| F**RDLzk−com**Fzk−comRDL | 零知识性承诺函数 |
| F**RDLzk−proof**Fzk−proofRDL | 零知识性承诺证明函数 |
| R**HPS−D**LRHPS−DL | 基于哈希证明系统的零知识功能函数 |
| F**RHPS−DLzk**FzkRHPS−DL | 零知识性哈希证明函数 |
| c**ontractbp**contractbp | 用于背书备份加密信息的智能合约 |
| c**ontractve**rcontractver | 用于验证共享公钥及签名的智能合约 |
其余未在表中列举的符号含义,请参照具体章节与公式推导。
1.2 哈希证明系统
哈希证明系统于2002年被CRAMER和SHOUP提出,用于设计选择密文安全的公钥加密(PKE)机制,是一类特殊的非交互式证明系统^[13]^ 。因为指定验证者的非交互系统中证明形式表现为哈希值,故被称为哈希证明系统。因为指定验证者的非交互系统中证明形式表现为哈希值,故被称为哈希证明系统。通常来说,哈希证明系统中存在一个实例集合X ,存在NP语言L ⊂ X ,使得L ={x ∈X |ω ∈W :(x ,ω )∈R }。其中R 是一种二元关系定义,L 为NP 语言集合,W 为证据集合。那么由语言系统( X ,L ,W ,R )组成的哈希证明系统算法由下面3种概率多项式时间算法组成^[14]^ 。
1)参数生成算法(Parameter Generation)Gen:生成密钥对( pr~key~ , pb~key~ ),pr~key~ 和pb~key~ 之间存在多对一的关系映射,即p**rkey→αpbkeyprkey→αpbkey,α 是一种映射关系。此外密钥pr~key~ 定义一个哈希函数hashpr:X→**Πhashpr:X→Π,其中 X 为实例空间,ΠΠ为证明空间。
2)私有求值算法(Private Evaluation)Pri:在算法Pri中,输入私钥pr~key~ ,可以快速计算求出hash~pr~ ( x ),x ∈X 。
3)公开求值算法(Public Evaluation)Pub:在算法Pub中,输入公钥pb~key~ ,可在无私钥的情形下计算出hash~pr~ (x ),前提是需要获取到x ∈L 中相应的证据ω ,即hash~pr~ (x )=Pub ( pb~key~ , x , ω )。
一般地,哈希证明系统具备两个特性,分别是平滑性和投射性。投射性是指对于x ∉L ,hash~pr~ (x )在证明空间Π 中随机分布,即如果私钥不相同,哈希值的产生也不相同,对于x ∈L ,hash~pr~ (x )的值可由公钥pb~key~ 和元素x 唯一确定,哈希值不变;平滑性是指一个有效密文x ∈L 与一个无效密文x ∉L 在哈希证明系统中的输出统计不可区分的。我们可以将具备较好平滑性和投影性的语言系统(X , L ,W , R )可视为一个有效的子群问题(Subnet Membership Problem)。
1.3 零知识证明
所谓的零知识证明,简而言之,就是不泄露具体信息前提下向别人证明自己知道某个信息。Zcash就是为了实现全部匿名交易,利用零知识证明的算法保证了交易无法被追溯和泄露^[15]^ 。从算法的设计上,零知识证明虽然在常见的隐私技术中算法简洁度比较差,但它的隐私程度相对较高。因此,自从2013年Pinocchio协议首次将零知识证明从理论带到应用到中以来(实现了分钟级证明,毫秒级验证)^[16]^ ,很多研究机构团体在零知识证明的算法及应用方面开展了研究与实现,例如斯坦福大学BUNZ^ [17]^ 等人提出的匿名支付协议Zether、WILLIAMSON ^[18]^ 提出的基于以太坊主网的隐私网络协议AZTEC,都采用零知识证明实现隐私保护。当前,应用最为广泛的零知识证明技术是zk-SNARKs,图1是zk-SNARKs的基本实现过程。
图1
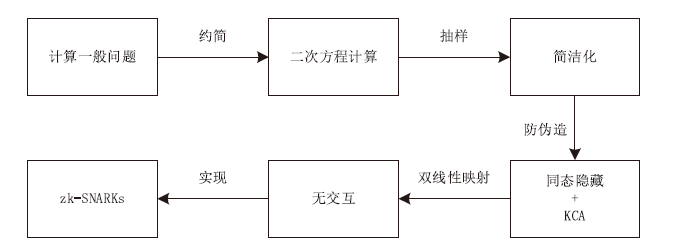
图1 zk-SNARKs的基本实现过程
首先,需要将一个一般问题经过计算约简成QAP (Quadratic Arithmetic Program)问题,再进行抽样实现算法的简洁性;其次对抽样点进行同态隐藏并进行KCA(Knowledge of Coefficient Test and Assumption),设置好共同参考数据集CRS)Common Reference String);最后进行数据的双线性映射,实现无交互的目的。
1.4 椭圆曲线数字签名算法
椭圆曲线数字签名算法是椭圆曲线密码体制 (ECC)对数字签名DSA的模拟,在加密货币中ECDSA算法实现一般是对交易中哈希形式的数据信息进行签名然后利用用户的私钥进行签名的认证。ECDSA主要由密钥生成算法、签名算法、验证算法3部分组成。
1)密钥生成算法
给定算法函数Genkey (G~q~ ,q ,G ),有如下密钥生成方式:Genkey (G~q~ ,q ,G )→(k , K )。其中G~q~ 是阶数为q 的椭圆曲线群,拥有基点G ,k ∈Z~q~ ,为ECDSA算法的私有输入密钥,K 为基于k 的公钥。密钥生成方式为:K =kG 。
2)签名算法
给定签名算法函数Sign (k , m ),有如下算法生成方式:Sign (k ,m )→(r ,s )。其中m 是待签名的消息,s 为签名,r 是有关R 横坐标分量r~x~ 的映射关系,取样a ∈Z~q~ ^^ ,有R =aG =(r~x~ ,r~y~ ),那么r 就可表示为r ←x mod q 。如果r 计算返回值为0,则重新选择a 进行计算;最后对待签名消息进行hash 处理计算签名s ←a ^-1^ hash (m )+rk mod q 。给出签名对(r , s ),并序列化为字节流和签名消息m* 送出进行验证。
3)验证算法
给定验证算法函数Verify (K , m , (r , s )),有如下验证方式:P =s ^-1^ hash (m )+rkG =aG →(x~p~ , y~p~ )。如果r ←x~p~ mod q 成立,则验证方可证实签名有效。
2 签名算法与安全模型
当前,较为适合实现安全多方计算的数字签名技术是Schnorr签名以及BLS签名,因为自身具备同态特性可以进行公钥聚合然后签名消息通过线性等式验证。而相比之下,ECDSA相对复杂,因为验证的等式并不是线性的。为了使得ECDSA能够在现今多方计算场景中得以被使用,需要对原有ECDSA进行改造。鉴于Castagnos提出的基于HPS的两方椭圆曲线数字签名算法(2P-ECDSA)方案,给出2P-ECDSA的安全模型密钥生成阶段,如图2所示。
图2
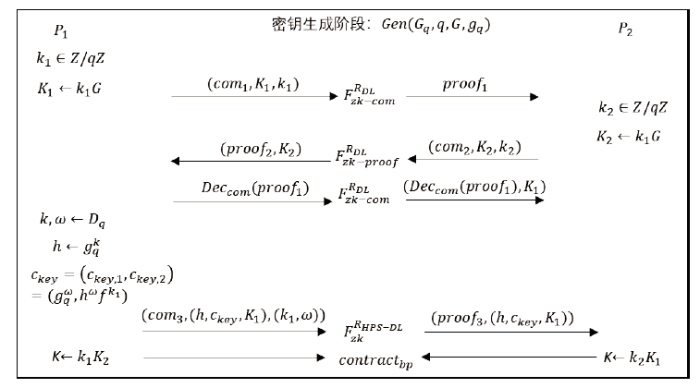
图2 2P-ECDSA的安全模型密钥生成阶段
从图2可以看出,给定的2P-ECDSA的安全模型主要分为密钥生成和签名验证两个阶段,在密钥生成阶段Gen (G~q~ ,q ,G ,g~q~ )中,相关的密钥信息的交互是由签名双方在链下进行的,其中g~q~ 是以阶数q 为基准的本原元。生成步骤如下:
1)签名参与方P ~1~ 首先借助自己的私有输入密钥k ~1~ 生成共享密钥K ~1~ ,然后将k ~1~ ,K ~1~ 以及有关k ~1~ 知识证明的承诺com ~1~ 传入零知识性承诺函数F**RDLzk−comFzk−comRDL中,上标R~DL~ 代表零知识性功能函数,用于证明给定的椭圆曲线点的离散对数知识,特征数式为R~DL~ :={(K ,ω )|K =ωG }。在经过FRDLzk−co**mFzk−comRDL处理之后,输出证明proof ~1~ ,传递给P ~2~ 处理;
2)签名参与方P ~2~ 确认接收到证明proof ~1~ 后,使用私有输入密钥k ~2~ 生成共享密钥K ~2~ ,然后将k ~2~ ,K ~2~ 以及有关k ~2~ 知识证明的承诺com ~2~ 传入零知识性承诺证明函数F**RDLzk−proofFzk−proofRDL中,在经过FRDLzk−proo**fFzk−proofRDL处理之后,输出证明proof ~2~ ,传递给P ~1~ 处理。
3)P ~1~ 接收到确认接收到proof ~2~ 之后,对原有证明proof ~1~ 进行拆解,然后再次送入零知识性函数F**RDLzk−com*Fzk−comRDL进行处理,将证明proof ~1~ 的拆解内容Dec~com~ ( proof ~1~ )连同共享密钥K* ~1~ 进行预存。
4)P ~1~ 私下从q 阶离散点集分布D~q~ 中取样私密输入k 以及ω ,然后利用k 投影生成哈希钥h 。接着通过k ,ω 以及h 产生用于二次零知识性证明的加密值c~k~ ey ,需要注意的是图中的f 是证明空间ΠΠ的一个循环子群。加密值c~key~ 给定完成后,需要将有关私密输入对(k ~1~ ,ω )知识的承诺com ~3~ ,公共参数组(h ,c~key~ ,K ~1~ )以及私密输入对(k ~1~ ,ω )送至零知识性哈希证明函数F**RHPS−DLzkFzkRHPS−DL处理,其中上标RHPS−DLRHPS−DL指代基于哈希证明系统的零知识性功能函数,用于证明加密的随机性知识、给定椭圆曲线离散对数基点K ~1~ 的知识以及有关加密了私密输入k ~1~ 的密文对(c~key~ ~,1~ ,c~key~ ~,2~ )知识,即c~key~ 。在经过FRHPS−DLz**kFzkRHPS−DL处理之后,输出证明proof ~3~ 以及公共参数组(h ,c~key~ ,K ~1~ )交由P ~2~ 留存。
5)P ~1~ 、P ~2~ 分别私下计算统合公钥K ,然后需提交至区块链合约contract~bp~ 上进行备份存根。
通过使用具备零知识性的功能函数F**RDLzk−comFzk−comRDL、FRDLzk−proo**fFzk−proofRDL以及F**RHPS−DLzk**FzkRHPS−DL进行私密信息的处理,将签名参与双方在密钥生成阶段的隐私信息进行封装,对于每次进行零知识函数处理生成的证明,如果接受方接受不到,将会终止接下来的信息交换流程,也就相应无区块链链上操作,减少额外通信的损耗。
在密钥生成阶段处理完成后,便会进入签名阶段Sign (m , seed ),流程如图3所示。
图3

图3 2P-ECDSA安全模型签名阶段
从图3中可以看出,对于给定签名消息m 以及用于消息标识的随机数seed ,签名双方交互有如下步骤:
1)~3)与密钥生成阶段操作相仿,唯一区别在于每次传输消息数据时多了消息标识seed ,其中seed ~1~ 代表来自签名参与方P ~1~ 的标识,seed ~2~ 代表来自签名参与方P ~2~ 的标识。以便于在签名阶段对每次输出传输的数据流进行更为精准的判别;
4)P ~1~ 、P ~2~ 分别私下计算用于ECDSA验证算法的椭圆曲线点R ,然后将R 的横坐标r~x~ 抽取出来,由签名双方分别对其进行取模运算生成r ,并传输至合约contract~ver~ 中进行存根比对,如果比对成功,可以进行下一步签名流转;
5)签名参与方P ~2~ 对消息m 进行哈希处理产生m' ,紧接着调取r 、a ~2~ 、m' 以及密钥生成阶段P ~1~ 传输过来的哈希钥h 生成加密值c ~1~ 以及基于c~key~ 生成的加密输入c ~2~ 进行组合运算生成c ~3~ ,并将其传给P ~1~ ;
6)由签名参与方P ~1~ 利用投影哈希函数的可分解性对c ~3~ 进行解密以便获得随机变量α 计算签名的乘幂s**̂ **s^。
7)取s**̂ s^与q−s**̂ q−s^的最小值作为签名s ,最终将签名对(r , s )交付区块链上合约contract~ver~ 进行核验。
8)合约验证签名(r , s )是否正确,验证通过返回1,否则返回0。因验证过程与椭圆曲线签名算法ECDSA的验证过程相同,故不再进行过多赘述。
3 区块链方案测评
3.1 理论架构设计
本文采用第2章中的算法和安全模型,给出融入区块链的哈希证明系统架构,如图4所示。可以看出,该系统架构由3个模块组成:可证数据流转协议模块、哈希证明系统中间件模块和区块链模块。
图4

图4 融入区块链的哈希证明系统架构
可证数据协议负责处理可信数据流转,本架构拟采用哈希证明文件(Hash Proof File Protocol)进行模块设计。在该协议内部嵌入了第3部分的安全模型与算法结构、需要签名的真实信息数据以及哈希证明中间件的指向。通过哈希证明中间件位置信息定位到哈希证明系统中间件将安全模型与算法结构桥接到哈希证明系统中间件中进行信息的交互。哈希证明系统中间件则包括两个部分,身份认证中间件以及哈希证明中间件,为了在签名过程中加强参与方之间的可信度,需经过身份认证中间件进行基本核验评判,然后再进入哈希证明中间件进行2P-ECDSA算法实现。根据密钥生成阶段与签名阶段,在进行哈希证明2P-ECDSA算法协议时,需要与区块链数据进行流转,借助智能合约比对验证共享密钥的正确性、签名的合法性等。此外,对于签名消息,也需要借助单向函数进行哈希处理,进行备份保存。
之所以可证数据流转协议中利用哈希证明中间件位置信息先指向哈希证明中间件而不直接指向区块链,是因为参与方不能直接对链数据操作来证明签名信息的可靠,因为代价开销过高,且通过区块节点位置查找证明内容并不方便。但证明中间件是可被经过身份认证的参与方利用链数据来验证的,从而在保证公共存储的公钥数据、签名数据等难以篡改,以建立可信实用的哈希证明系统。
对于该HPFS架构,区块链的链式结构使得哈希证明进一步实现了算法协议控制权声明与数据信息控制权使用的分离,解决信息泄露、信息不可信的问题。一方面,算法的定义与使用在链下进行实现的同时,需要与区块链进行交互对公钥数据、签名信息等进行备份以防在算法协议声明时发生信息篡改;另一方面,借助智能合约也能够在签名验证阶段进行算法自治,对不合法签名予以否认,并仅对共享数据进行哈希处理,使得签名双方保有私有信息时可借助区块链与公共数据建立逻辑纽带,从而释放签名者的隐私数据价值。此外,因为分布式网络中任何人都可以拉取区块链,所以区块链网络上的参与者都可以利用链数据进行验证,从而增强了该哈希证明系统的可靠性。
3.2 安全性分析
3.2.1 基于模拟的安全证明
通常密码学领域安全性证明主要分为两种,一种是基于博弈的安全(Proofs Based on Simulation),一种是基于模拟的安全(Proofs Based on Games)。对于基于博弈的安全,安全性一般是由博弈的过程来判定的。而基于模拟的安全,则是由自己设定的模拟器和理想函数而定的。所以从语义安全上看,基于模拟的安全性证明更加能确定它的正确性。即若敌手获取某消息密文而模拟器未得到,那么敌手此时能计算的所有有关该消息的信息模拟器也是可以计算的,则加密安全^[6]^ 。
本文拟定了3个具备零知识性的理想功能函数:F**RDLzk−comFzk−comRDL、 FRDLzk−proo**fFzk−proofRDL、F**RHPS−DLzk*FzkRHPS−DL,给定模拟器σ ,那么所有这些理想功能函数的执行将会在σ 被执行,输入参数会经过模拟器σ 传入指定功能函数然后在函数体内执行完成之后将会再次通过模拟器σ 被输出出来。为了证明该基于HPS的2P-ECDSA算法协议在存在单一恶意敌手情况下的不可区分性,下面将模拟存在恶意参与方P ~1~ 和存在恶意参与方P* ~2~ 两种情形进行安全分析。
1)存在恶意参与方P ~1~ 。给定模拟器σ ,在密钥生成步骤将会验证K ~1~ =k ~1~ G 是否成立,如果不成立,那么σ 将在密钥生成步骤3)中模拟出参与方P ~2~ 中止流程的情况。如果成立,那么σ 将会通过提取的私密输入k ~1~ 验证P ~1~ 私下计算的c**key**=(g**qω,hωfk**1)ckey=(gωq,hωfk1)是否成立,如果不成立,那么σ 将在密钥生成步骤4)中模拟出参与方P ~2~ 中止流程的情况。相应地,在签名步骤σ 将会验证R ~1~ =a ~1~ G 是否成立,如果不成立,那么σ 将会在签名步骤3)中模拟出参与方P ~2~ 中止流程的情况。如果成立,将会继续生成最终共享公钥K 供签名步骤计算核验签名。
2)存在恶意参与方P ~2~ 。在密钥生成步骤,σ 将会通过提取的私密输入k ~2~ 验证P ~2~ 计算K ~2~ 是否是椭圆曲线上的非零点使得K ~2~ =k ~1~ G 。如果不成立,那么σ 将在密钥生成步骤2)中模拟出参与方P ~1~ 中止流程的情况。如果成立,那么将继续进行理想的ECDSA功能函数,使参与方P ~1~ 接受输入,然后进行共享公钥K 的链上合约存储备份。在签名步骤,σ 将会通过提取的私密输入a ~2~ 验证P ~2~ 计算R ~2~ 是否是椭圆曲线上的非零点使得R ~2~ =k ~2~ G 成立。如果不成立,那么σ 将在签名步骤2)中模拟出参与方P ~1~ 中止流程,不再进行签名计算。如果成立,那么σ 将接收从P ~2~ 传入过来的c ~3~ ,根据α = a ~2~ ^-1^ m '+ rx ~2~ x ~1 ~ mod q 进行判别,如果σ 成立,诚实参与方P ~1~ 将会接收输入进行校验,否则算法将会中止。
综合上述两种情形的分析,在与诚实参与方P~i~ , i ∈1,2交互时,经σ 输出的内容是不可区分的。因为σ 可以从基于哈希证明系统的零知识性功能函数R~HPS~ ~-~ ~DL~ 中提取私密输入k ~1~ ,换句话说,也就是发生恶意行为后可以重新计算密文并验证以获取加密值c~key~ 。另外,因为私密输入元素都源自于循环群Z /qZ ,所以在理想情形和实际情形中,私密输入的概率分布将会是相同的。通过设定模拟器σ 简要分析了存在恶意参与方的情形,展示了算法的存在性与零知识性,从而完成了模拟安全的证明。
此外,为了证明不可区分性,敌手必须要将原加密方案中的x ∈L 的元素替换为语言系统(X ,L ,W ,R )之外的x ∉L 元素,即将有效密文篡改为无效密文。但若想实行这种篡改,敌手又必须知道私密的哈希密钥,然而对于一个语言系统子集成员(X ,L ,W ,R )是一个子集成员困难问题时,那么在多项式时间内,敌手的这种篡改便不会成功,这一点不会被任何多项式时间的对手注意到。此外,因签名方案中的哈希证明系统的平滑性允许参与方用明文空间的某些随机值来替换当前的明文值,从而保证加密方案的不可区分性。
3.2.2 应用安全分析
该理论架构中,将哈希后的签名信息、密钥生成时的共享密钥信息以及签名对信息(**r,s**)(r,s)进行上链存储,通过合约对公开的数据信息进行检测认证,防止签名双方链下肆意篡改数据信息进行作恶。在哈希证明系统的中间件中额外添加了身份验证的机制,预先定义唯一的标识信息与签名者的隐匿身份信息进行关联,在身份验证中间件内部进行签名者身份的验证方式将会保证签名者的签名身份具有一定可信性。而针对算法定义、安全模型定义等涉及内部签名实现的原理级别内容,是在可证数据流转协议中进行了内部封装,只向外部服务提供需权限认证通过才可进行调用的接口,即在使用上进行了安全限制。
总而言之,基于HPS的2P-ECDSA算法,融合区块链实现分布式的哈希证明系统服务,将分布式的账本技术逐渐发展成为分布式的服务技术,业务层面上是从单纯的去中心化数据存储机制演变为去中心化的“数据+服务”。通过哈希证明构造语义安全的密码学签名算法,保障了数据的准确性与可信。一旦数据具备可信任的所属性,那么在此前提下便可进一步交换创造价值。
4 结束语
本文研究在CASTAGNOS^[9]^ 等人论文理论之上,实现可以融入区块链的基于HPS的2P-ECDSA方案理论,证实了该方案是基于模拟安全的,且具备良好隐私性。不过目前的方案仍有可以改进的地方,如在哈希证明系统中间中并未将身份认证中间件中判别签名者的算法协议进行具体的描述,需要更为详细的设计方案,我们正考虑在此中间件中融入多方参与的量子密钥分发手段^[20]^ 以实现安全、可双向验证的密钥分发协议。本文方案在后量子密码时代并不具备抵抗量子计算机的能力,设计一个更为安全的基于哈希证明系统的两方椭圆曲线签名依旧需要不断分析和深入研究。此外,下一步工作中会考虑将方案与多学科技术进行交叉融合,如大数据、人工智能等,将算法效率进行调优改进,以便结合真实案例场景进行合理布局。
参考文献 View Option
[1]KOBLITZ N.Elliptic Curve Cryptosystems
[J]. Mathematics of Computation, 1987,48(177):203-209.
DOI:10.1090/S0025-5718-1987-0866109-5 URL [本文引用: 1]
[2]MILLER V S.Use of Elliptic Curves in Cryptography
[C] // ACM. Lecture notes in computer sciences 218 on Advances in cryptology—-CRYPTO 85, August 18-22, 1985, Santa Barbara, California, USA. Heidelberg: Springer, 1986: 417-426.
[3]HU Y C, LABERTEAUX K P. Strong VANET Security on a Budget[EB/OL]. https://www.researchgate.net/publication/250004065_Strong_VANET_security_on_a_budget, 2020-06-19.
[4]ABUEH Y J, LIU H. Message Authentication in Driverless Cars[EB/OL]. https://ieeexplore.ieee.org/document/7568882, 2020-06-25.
[5]COURTOIS N, SONG G, CASTELLUCCI R.Speed Optimizations in Bitcoin Key Recovery Attacks
[J]. Tatra Mountains Mathematical Publications, 2016,67(1):55-68.
DOI:10.1515/tmmp-2016-0030 URL [本文引用: 1]
[6]CHEN Yuan, BAI Enjian, XIAO Guozhen.Equivalence Between Two Definitions of Semantic Security
[J]. Acta Electronica Sinica, 2009,37(10):2149-2153.
陈原, 白恩健, 肖国镇.两种语义安全性定义的等价性
[J]. 电子学报, 2009,37(10):2149-2153.
[7]YU Wei, LI Bao, WANG Kunpeng, et al.Co-z Montgomery Algorithm on Elliptic Curves over Finite Fields of Characteristic Three
[J]. Chinese Journal of Computers, 2017,40(5):1121-1133.
于伟, 李宝, 王鲲鹏, 等.特征3有限域上椭圆曲线的co-Z Montgomery算法
[J]. 计算机学报, 2017,40(5):1121-1133.
[8]CAMPBELL Sr R.Evaluation of Post-quantum Distributed Ledger Cryptography
[J]. The Journal of the British Blockchain Association, 2019,2(1):7679.
[9]CASTAGNOS G, CATALANO D, LAGUILLAUMIE F, et al. Two-party ECDSA from Hash Proof Systems and Efficient Instantiations[EB/OL]. https://www.researchgate.net/publication/335077814_Two-Party_ECDSA_from_Hash_Proof_Systems_and_Efficient_Instantiations, 2020-06-29.
[10]LINDELL Y. Fast Secure Two-party ECDSA Signing[EB/OL]. https://xueshu.baidu.com/usercenter/paper/show?paperid=14579863a345247cf28a724049a82c78&site=xueshu_se, 2020-06-30.
[11]DOERNER J, KONDI Y, LEE E, et al. Secure Two-party Threshold ECDSA from ECDSA Assumptions[EB/OL]. https://www.computer.org/csdl/pds/api/csdl/proceedings/download-article/12OmNvDI3J1/pdf, 2020-07-10.
[12]LINDELL Y, NOF A. Fast Secure Multiparty ECDSA with Practical Distributed Key Generation and Applications to Cryptocurrency Custody[EB/OL]. https://xueshu.baidu.com/usercenter/paper/show?paperid=114400w0xs5q04p0625h0vf05b514642&site=xueshu_se, 2020-07-13.
[13]CRAMER R, SHOUP V. Universal Hash Proofs and a Paradigm for Adaptive Chosen Ciphertext Secure Public-key Encryption[EB/OL]. https://xueshu.baidu.com/usercenter/paper/show?paperid=114400w0xs5q04p0625h0vf05b514642&site=xueshu_se, 2020-07-15.
[14]LAI Qiqi, YANG Bo, YU Yong, et al.A Survey on the Construction of Hash Proof Systems Based on Lattices
Journal of Cryptologic Research, 2017,4(5):474-484.
来齐齐, 杨波, 禹勇, 等.基于格的哈希证明系统的构造综述
[J]. 密码学报, 2017,4(5):474-484.
[15]HOPWOOD D, BOWE S, HORNBY T, et al. Zcash Protocol Specification[EB/OL]. , 2020-07-19.
[16]PARNO B, HOWELL J, GENTRY C, et al. Pinocchio: Nearly Practical Verifiable Computation[EB/OL]. http://www.andrew.cmu.edu/user/bparno/papers/pinocchio-cacm.pdf, 2020-07-20.
[17]BUNZ B, AGRAWAL S, ZAMANI M, et al. Zether: Towards Privacy in a Smart Contract World[EB/OL]. https://www.researchgate.net/publication/343032027_Zether_Towards_Privacy_in_a_Smart_Contract_World, 2020-07-22.
[18]WILLIAMSON Z J. The Aztec Protocol[EB/OL]. https://github.com/AztecProtocol/AZTEC, 2020-07-25.
- 零知识编年史:群 114 浏览
- zkMesh:2026年2月回顾 265 浏览
- zkMesh:2026年1月回顾 509 浏览
- 使用 Ecash 票据的谨慎日志合约 417 浏览
- Vitalik: 2026年我对使用的软件做了两个重大改变 638 浏览
- Fiat-Shamir 启发式非交互式零知识证明之美(以及 Zig) 661 浏览
- 基于密码学的安全联邦学习 631 浏览
- 扳手攻击:发生与预防 631 浏览
- 在浏览器中生成零知识证明, 今天就可以 729 浏览
- ZK Mesh:2025年12月回顾 782 浏览
- DahLIAS:既非 ECDSA,也非 Schnorr 626 浏览
- 安全研究人员的数学指南 942 浏览


