Bitlayer Research:Binius STARKs原理解析与优化思考
- Bitlayer Labs
- 发布于 2024-10-22 10:28
- 阅读 2730
第1,2,3代STARK证明系统位宽分别为252,64和32bit,编码效率虽有提高,但仍有浪费空间;Binius直接对位操作,编码紧凑高效,很可能是未来的第4代STARK。

作者:mutourend & lynndell
1. 引言
区别于基于椭圆曲线的SNARKs,可将STARKs看成是hash-based SNARKs。当前STARKs效率低下的一个主要原因是:实际程序中的大多数数值都较小,如for循环中的索引、真假值、计数器等。然而,为了确保基于Merkle树证明的安全性,使用Reed-Solomon编码对数据进行扩展时,许多额外的冗余值会占据整个域,即使原始值本身非常小。为解决该问题,降低域的大小成为了关键策略。
如表1所示,第1代STARKs编码位宽为252bit,第2代STARKs编码位宽为64bit,第3代STARKs编码位宽为32bit,但32bit编码位宽仍然存在大量的浪费空间。相较而言,二进制域允许直接对位进行操作,编码紧凑高效而无任意浪费空间,即第4代STARKs。
| 表 1: STARKs衍化路径 | STARKs | 基域 | 基域位宽 | 编码效率(越大越好) | 扩域 | 典型代表 |
|---|---|---|---|---|---|---|
| 第1代 | $p=2^{251}+17\cdot 2^{192}+1$ | 252 bits | 1 | - | Stone | |
| 第2代 | $p=2^{64}-2^{32}+1$ | 64 bits | 2 | 2次扩域 | Plonky2, Polygon zkEVM, zkSync zkEVM | |
| 第3代 | $p=2^{31}-2^{27}+1$ | 32 bits | 3 | 4次扩域 | RISC Zero | |
| $p=2^{31}-1$ | 32 bits | 3 | 4次扩域 | Plonky3, Stwo | ||
| 第4代 | $p=1$ | 1 bit | 4 | 128次扩域 | Binius |
相比于Goldilocks、BabyBear、Mersenne31等近几年新研究发现的有限域,二进制域的研究可追溯到上个世纪80年代。当前,二进制域已经广泛应用于密码学中,典型例子包括:
- 高级加密标准 (AES) ,基于 $\mathbb{F}_{2^8}$ 域;
- Galois 消息认证码 (GMAC) ,基于 $\mathbb{F}_{2^{128}}$ 域;
- QR码 ,使用基于 $\mathbb{F}_{2^8}$ 的Reed-Solomon编码;
- 原始FRI和zk-STARK协议 ,以及进入SHA-3决赛的Grøstl 哈希函数,该函数基于 $\mathbb{F}_{2^8}$ 域,是一种非常适合递归的哈希算法。
当采用较小的域时,扩域操作对于确保安全性愈发重要。而Binius所使用的二进制域,需完全依赖扩域来保证其安全性和实际可用性。大多数Prover计算中涉及的多项式无需进入扩域,而只需在基域下操作,从而在小域中实现了高效率。然而,随机点检查和FRI计算仍需深入到更大的扩域中,以确保所需的安全性。基于二进制域来构建证明系统时,存在2个实际问题:STARKs中计算trace表示时,所用域大小应大于多项式的阶;STARKs中Merkle tree承诺时,需做Reed-Solomon编码,所用域大小应大于编码扩展后的大小。
Binius提出了一种创新的解决方案,分别处理这两个问题,并通过两种不同的方式表示相同的数据来实现:首先,使用多变量(具体是多线性)多项式代替单变量多项式,通过其在“超立方体”(hypercubes)上的取值来表示整个计算轨迹;其次,由于超立方体每个维度的长度均为2,因此无法像STARKs那样进行标准的Reed-Solomon扩展,但可以将超立方体视为方形(square),基于该方形进行Reed-Solomon扩展。这种方法在确保安全性的同时,极大提升了编码效率与计算性能。
2. 原理解析
当前大多数SNARKs系统的构建通常包含以下两部分:
- 信息理论多项式交互预言机证明(Information-Theoretic Polynomial Interactive Oracle Proof, PIOP): PIOP作为证明系统的核心,将输入的计算关系转化为可以验证的多项式等式。不同的PIOP协议通过与验证者的交互,允许证明者逐步发送多项式,使得验证者通过查询少量多项式的评估结果即可验证计算是否正确。现有的PIOP协议包括:PLONK PIOP、Spartan PIOP和HyperPlonk PIOP等,它们各自对多项式表达式的处理方式有所不同,从而影响整个SNARK系统的性能与效率。
- 多项式承诺方案(Polynomial Commitment Scheme, PCS): 多项式承诺方案用于证明PIOP生成的多项式等式是否成立。PCS是一种密码学工具,通过它,证明者可以承诺某个多项式并在稍后验证该多项式的评估结果,同时隐藏多项式的其他信息。常见的多项式承诺方案有KZG、Bulletproofs、FRI(Fast Reed-Solomon IOPP)和Brakedown等。不同的PCS具有不同的性能、安全性和适用场景。
根据具体需求,选择不同的PIOP和PCS,并结合合适的有限域或椭圆曲线,可以构建具有不同属性的证明系统。例如:
- Halo2: 由PLONK PIOP与Bulletproofs PCS结合,并基于Pasta曲线。Halo2设计时,注重于可扩展性,以及移除ZCash协议中的trusted setup。
- Plonky2: 采用PLONK PIOP与FRI PCS结合,并基于Goldilocks域。Plonky2是为了实现高效递归的。
在设计这些系统时,选择的PIOP和PCS必须与所使用的有限域或椭圆曲线相匹配,以确保系统的正确性、性能和安全性。这些组合的选择不仅影响SNARK的证明大小和验证效率,还决定了系统是否能够在无需可信设置的前提下实现透明性,是否可以支持递归证明或聚合证明等扩展功能。
Binius :HyperPlonk PIOP + Brakedown PCS + 二进制域。具体而言,Binius包括五项关键技术,以实现其高效性和安全性。首先,基于塔式二进制域(towers of binary fields)的算术化 构成了其计算的基础,能够在二进制域内实现简化的运算。其次,Binius在其交互式Oracle证明协议(PIOP)中,改编了HyperPlonk乘积与置换检查 ,确保了变量及其置换之间的安全高效的一致性检查。第三,协议引入了一个新的多线性移位论证 ,优化了在小域上验证多线性关系的效率。第四,Binius采用了改进版的Lasso查找论证 ,为查找机制提供了灵活性和强大的安全性。最后,协议使用了小域多项式承诺方案(Small-Field PCS) ,使其能够在二进制域上实现高效的证明系统,并减少了通常与大域相关的开销。
2.1 有限域:基于towers of binary fields的算术化
塔式二进制域是实现快速可验证计算的关键,主要归因于两个方面:高效计算 和高效算术化 。二进制域本质上支持高度高效的算术操作,使其成为对性能要求敏感的密码学应用的理想选择。此外,二进制域结构支持简化的算术化过程,即在二进制域上执行的运算可以以紧凑且易于验证的代数形式表示。这些特性,加上能够通过塔结构充分利用其层次化的特性,使得二进制域特别适合于诸如Binius这样可扩展的证明系统。
| 表 2: 素数域 $\mathbb{F}p$ 与二元域 $\mathbb{F}{2^k}$ 对比 | 素数域$\mathbb{F}_p$ | 二进制域$\mathbb{F}_{2^k}$ | |
|---|---|---|---|
| 表示 | Not canonical | Canonical | |
| 加法运算 | 为带条件的整数加法(即模加运算) | 为bitwise XOR运算 | |
| 乘法运算 | 为带reduction方法的整数乘法(即模乘运算) | 为带reduction方法的carryless无进位乘法运算(为多项式乘法) |
其中“canonical”是指在二进制域中元素的唯一且直接的表示方式。例如,在最基本的二进制域 $\mathbb{F}_2$ 中,任意k位的字符串都可以直接映射到一个k位的二进制域元素。这与素数域不同,素数域无法在给定位数内提供这种规范的表示。尽管32位的素数域可以包含在32位中,但并非每个32位的字符串都能唯一地对应一个域元素,而二进制域则具备这种一对一映射的便利性。在素数域$\mathbb{F}p$中,常见的归约方法包括 Barrett归约 、Montgomery归约 ,以及针对Mersenne-31 或Goldilocks-64 等特定有限域的特殊归约方法。在二进制域 $\mathbb{F}{2^k}$ 中,常用的归约方法包括 特殊归约 (如AES中使用)、Montgomery归约 (如POLYVAL中使用)和递归归约 (如Tower)。论文《Exploring the Design Space of Prime Field vs. Binary Field ECC-Hardware Implementations》指出,二进制域在加法和乘法运算中均无需引入进位,且二进制域的平方运算非常高效,因为它遵循$(X + Y)^2 = X^2 + Y^2$的简化规则。
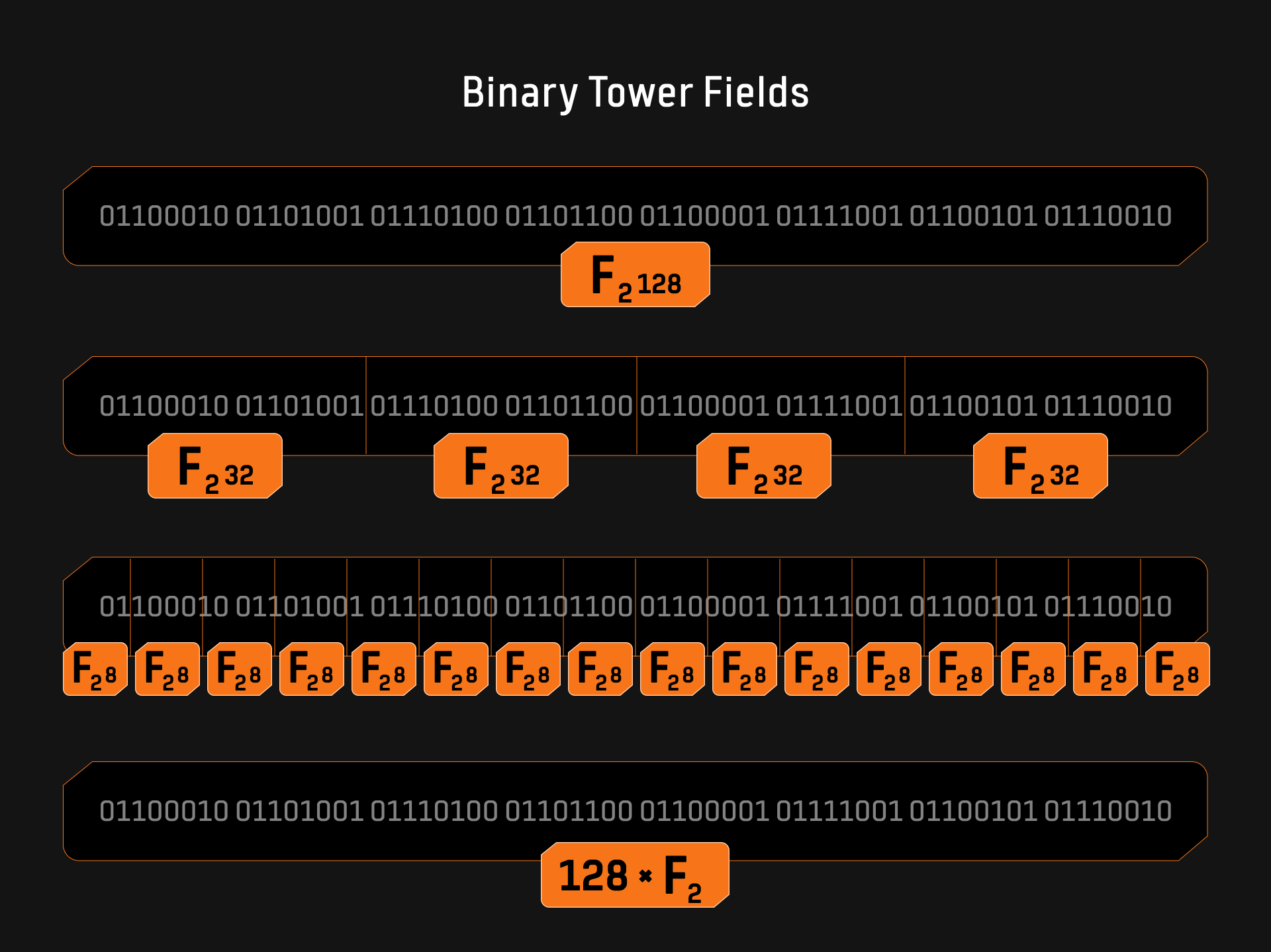
如图2所示,一个128位字符串:该字符串可以在二进制域的上下文中以多种方式进行解释。它可以被视为128位二进制域中的一个独特元素,或者被解析为两个64位塔域元素、四个32位塔域元素、16个8位塔域元素,或128个 $\mathbb{F}_2$ 域元素。这种表示的灵活性不需要任何计算开销,只是对位字符串的类型转换(typecast),是一个非常有趣且有用的属性。同时,小域元素可以被打包为更大的域元素而不需要额外的计算开销。Binius协议利用了这一特性,以提高计算效率。此外,论文《On Efficient Inversion in Tower Fields of Characteristic Two》探讨了在$n$位塔式二进制域中(可分解为$m$位子域)进行乘法、平方和求逆运算的计算复杂度。
| 表 3: 域运算的复杂度 | 乘法运算 | m-bit子域乘法运算 | 平方运算 | 求逆运算 |
|---|---|---|---|---|
| $O(n^{1.58})$ | $O(nm^{0.58})$ | $O(n\log n)$ | $O(n^{1.58})$ |
2.2 PIOP:改编版HyperPlonk Product和Permutation Check——适用于二进制域
Binius协议中的PIOP设计借鉴了HyperPlonk,采用了一系列核心检查机制,用于验证多项式和多变量集合的正确性。这些核心检查包括:
- GateCheck: 验证保密见证$\omega$和公开输入$x$是否满足电路运算关系$C(x,\omega)=0$,以确保电路正确运行。
- PermutationCheck: 验证两个多变量多项式$f$和$g$在布尔超立方体上的求值结果是否为置换关系$f(x)=f(\pi(x))$,以确保多项式变量之间的排列一致性。
- LookupCheck: 验证多项式的求值是否在给定的查找表中,即$f(B\mu )\subseteq T(B\mu )$,确保某些值在指定范围内。
- MultisetCheck: 检查两个多变量集合是否相等,即${(x{1,i},x{2,i})}{i\in H} = {(y{1,i},y{2,i})}{i\in H}$,保证多个集合间的一致性。
- ProductCheck: 检测有理多项式在布尔超立方体上的求值是否等于某个声明的值$\prod{x\in H\mu }f(x)=s$,以确保多项式乘积的正确性。
- ZeroCheck: 验证一个多变量多项式在布尔超立方体上的任意点是否为零$\prod{x\in H\mu }f(x)=0, \forall x\in B_\mu $,以确保多项式的零点分布。
- SumCheck: 检测多变量多项式的求和值是否为声明的值$\sum{x\in H\mu }f(x)=s$。通过将多元多项式的求值问题转化为单变量多项式求值,降低验证方的计算复杂度。此外,SumCheck还允许批处理,通过引入随机数,构造线性组合实现对多个和校验实例的批处理。
- BatchCheck: 基于SumCheck,验证多个多变量多项式求值的正确性,以提高协议效率。
尽管Binius与HyperPlonk在协议设计上有许多相似之处,但Binius在以下3个方面做出改进:
- ProductCheck优化: 在HyperPlonk中,ProductCheck要求分母$U$在超立方体上处处非零,且乘积必须等于一个特定值;Binius通过将该值特化为1,简化这一检查过程,从而降低计算复杂度。
- 除零问题的处理: HyperPlonk未能充分处理除零情况,导致无法断言$U$在超立方体上的非零问题;Binius正确地处理了这一问题,即使在分母为零的情况下,Binius的ProductCheck也能继续处理,允许推广到任意乘积值。
- 跨列PermutationCheck: HyperPlonk无此功能;Binius支持在多个列之间进行PermutationCheck,这使得Binius能够处理更复杂的多项式排列情况。
因此,Binius通过对现有PIOP SumCheck机制的改进,提升了协议的灵活性和效率,尤其在处理更复杂的多变量多项式验证时,提供了更强的功能支持。这些改进不仅解决了HyperPlonk中的局限性,还为未来基于二进制域的证明系统奠定了基础。
2.3 PIOP:新的multilinear shift argument——适用于boolean hypercube
在Binius协议中,虚拟多项式的构造和处理是关键技术之一,能够有效地生成和操作从输入句柄或其他虚拟多项式派生出的多项式。以下是两个关键方法:
- Packing: 该方法通过将词典序中相邻位置的较小元素打包成更大的元素来优化操作。Pack运算符针对大小为$2^\kappa$的块操作,并将它们组合成高维域中的单个元素。通过多线性扩展(Multilinear Extension, MLE),这个虚拟多项式可以高效地评估和处理,将函数$t$转换为另一个多项式,从而提高了计算性能。
- 移位运算符: 移位运算符重新排列块内的元素,基于给定偏移量$o$进行循环移位。该方法适用于大小为$2^b$的块,每个块根据偏移量执行移位。移位运算符通过检测函数的支持来进行定义,确保在处理虚拟多项式时保持一致性和效率。评估该构造的复杂度随块大小线性增长,特别适用于处理大数据集或布尔超立方体中的高维场景。
2.4 PIOP:改编版Lasso lookup argument——适用于二进制域
Lasso协议允许证明方承诺一个向量$a \in \mathbb{F}^m$,并证明其所有元素均存在于一个预先指定的表$t \in \mathbb{F}^n$中。Lasso解锁了“查找奇点”(lookup singularities)的概念,并能适用于多线性多项式承诺方案。其效率体现在以下两个方面:
-
证明效率: 对于大小为$n$的表中的$m$次查找,证明方只需承诺$m + n$个域元素。这些域元素很小,均位于集合${0, \dots, m}$中。在基于多次幂运算的承诺方案中,证明方的计算成本为$O(m + n)$次群运算(如椭圆曲线点加),外加证明多线性多项式在布尔超立方体上是否为表元素的求值成本。
-
无需承诺大表: 如果表$t$是结构化的,则无需对其进行承诺,因此可以处理超大表(如$2^{128}$或更大)。证明方的运行时间仅与访问的表条目相关。对于任意整数参数$c > 1$,证明方的主要成本是证明大小,承诺的域元素为$3 \cdot c \cdot m + c \cdot n^{1/c}$个。这些域元素都是较小的,位于集合${0, \dots, \max{m, n^{1/c}, q} - 1}$中,其中$q$为$a$中的最大值。
Lasso协议由以下三个组件构成:
- 大表的虚拟多项式抽象: 通过将虚拟多项式组合,实现在大表上的操作,确保在表内进行高效的查找和处理。
- 小表查找: Lasso的核心是小表查找,作为虚拟多项式协议的核心构建,使用离线内存检测验证一个虚拟多项式在布尔超立方体上的求值是否是另一个虚拟多项式求值的子集。这一查找过程将归约为多集合检测的任务。
- 多集合检查: Lasso引入虚拟协议来执行多集合检查,验证两个集合的元素是否相等或满足特定条件。
Binius协议将Lasso适应于二进制域的操作,假设当前域是一个大特征的素数域(远大于被查找列的长度)。Binius引入了乘法版本的Lasso协议,要求证明方和验证方联合递增协议的“内存计数”操作,不是通过简单的加1递增,而是通过二进制域中的乘法生成元来递增。然而,这一乘法改编引入了更多的复杂性,与递增操作不同,乘法生成元并非在所有情况下递增,在0处存在单一轨道,这可能成为攻击点。为防止这种潜在的攻击,证明方必须承诺一个处处非零的读取计数向量,以确保协议的安全性。
2.5 PCS:改编版Brakedown PCS——适用于Small-Field
构建Binius PCS的核心思想是packing。Binius论文中提供了2种基于二进制域的Brakedown多项式承诺方案:一种是采用concatenated code来实例化;另一种采用block-level encoding技术,支持单独使用Reed-Solomon codes。第二种Brakedown PCS方案,简化了证明和验证流程,但proof size要比第一种略大一点,但所带来的简化和实现优势,做该取舍是值得的。
Binius多项式承诺主要使用小域多项式承诺与扩展域评估、小域通用构造和块级编码与Reed-Solomon码技术。
-
小域多项式承诺与扩展域评估: Binius协议中的承诺是在小域$K$上的多项式承诺,并在更大的扩展域$L/K$中进行评估。这种方法确保了每个多线性多项式$t(X0,\dots,X{\ell-1})$属于域$K[X0,\dots,X{\ell-1}]$,而评估点可以位于更大扩展域$L$中。承诺方案专门设计用于小域多项式,并能在扩展域上进行查询,同时保证承诺的安全性和效率。
-
小域通用构造: 小域通用构造通过定义参数$\ell$、域$K$及其相关的线性块码$C$,确保扩展域$L$足够大,以支持安全评估。为了在保持计算效率的同时提高安全性,协议通过扩展域的特性,以及采用线性块码对多项式进行编码,保证了承诺的稳健性。
-
块级编码与Reed-Solomon码: 针对字段比线性块码字母表更小的多项式,Binius提出了块级编码方案。通过这一方案,即使在小域(如$\mathbb{F}2$)中定义的多项式,也可以使用如$\mathbb{F}{2^{16}}$这样的大字母表的Reed-Solomon码高效承诺。Reed-Solomon码之所以被选中,是因为它具有高效性和最大距离分离特性。该方案通过将消息打包并逐行编码,之后利用Merkle树进行承诺,简化了操作复杂度。块级编码允许小域多项式的高效承诺,而不会产生通常与大域相关的高计算开销,从而使得在$\mathbb{F}_2$等小域中承诺多项式成为可能,并在生成证明与验证中保持计算效率。
3. 优化思考
为了进一步提升Binius协议的性能,本文提出了四个关键优化点:
- GKR-based PIOP: 针对二进制域乘法运算,借助GKR协议,来替换Binius论文中的的Lasso Lookup算法,可大幅降低Binius的承诺开销;
- ZeroCheck PIOP 优化: 在Prover与Verifier之间进行计算开销权衡,使得ZeroCheck操作更加高效;
- Sumcheck PIOP 优化: 针对小域Sumcheck的优化,进一步减少了小域上的计算负担;
- PCS优化: 通过FRI-Binius优化,降低证明大小,提高协议的整体性能。
3.1 GKR-based PIOP:基于GKR的二进制域乘法
Binius论文引入一种基于lookup的方案,旨在实现高效的二进制域乘法运算。通过Lasso lookup argument改编的二进制域乘法算法依赖于lookups和加法操作的线性关系,这些操作与单个word中的limbs数量成比例。虽然这一算法在某种程度上优化了乘法操作,但仍需要与limbs数量线性相关的辅助承诺。
GKR(Goldwasser-Kalai-Rothblum)协议中的核心思想是,证明方(P)和验证方(V)针对一个有限域$\mathbb{F}$上的layered算术电路达成一致。该电路的每个节点有两个输入,用于计算所需的函数。为了减少验证方的计算复杂度,协议使用SumCheck协议,将关于电路输出门值的声明逐步简化为更低层的门值声明,直至最终将声明简化到关于输入的陈述。这样,验证方只需检查电路输入的正确性即可。
基于GKR的整数乘法运算算法,通过将“检查2个32-bit整数$A$和$B$是否满足$A\cdot B \overset{?}{=} C$”,转换为“检查$\mathbb{F}_{2^{64}}^*$ 中 $(g^A)^B\overset{?}{=}g^C$ 是否成立”,借助GKR协议大幅减少承诺开销。与之前的Binius lookup方案相比,基于GKR的二进制域乘法运算只需一个辅助承诺,并且通过减少Sumchecks的开销,使该算法更加高效,特别是在Sumchecks操作比承诺生成更便宜的场景下。随着Binius优化的推进,基于GKR的乘法运算逐渐成为减少二进制域多项式承诺开销的有效途径。
3.2 ZeroCheck PIOP优化:Prover与Verifier计算开销权衡
论文《Some Improvements for the PIOP for ZeroCheck》在证明方(P)和验证方(V)之间调整工作量的分配,提出了多种优化方案,以权衡开销。该工作探索了不同的$k$值配置,使得在证明方和验证方之间达成了成本的权衡,特别是在减少传输数据和降低计算复杂性方面。
1. 减少证明方的数据传输 通过将一部分工作转移给验证方V,从而降低证明方P发送的数据量。在第$i$轮中,证明方P需要向验证方V发送$v_{i+1}(X)$,其中$X=0,\dots,d+1$。验证方V检查以下等式以验证数据的正确性 $$vi = v{i+1}(0) + v{i+1}(1).$$ 优化为: 证明方 P 可以选择不发送$v{i+1}(1)$,而是让验证方 V 自行通过以下方式计算出该值 $$v_{i+1}(1) = vi - v{i+1}(0).$$ 此外,在第0轮,诚实的证明方 P 始终发送$v_1(0)=v1(1)=0$,这意味着无需进行任何评估计算,从而显著减少了计算和传输成本,降低至$d2^{n-1}C\mathbb{F} + (d + 1)2^{n-1}C_\mathbb{G}$。
2. 减少证明方评估点的数量 在协议的第 $i$ 轮中,验证者在之前的$i$轮中已经发送了一个值序列 $r = (r0, \dots, r{i-1})$。 当前协议要求证明者 ($P$) 发送多项式 $$v{i+1}(X) = \sum{x \in H_{n-i-1}} \hat{\delta}n(\alpha, (r, X, x)) C(r, X, x).$$ 优化为: 证明方 P 发送以下多项式 $$v{i+1}'(X) = \sum{x \in H{n-i-1}} \hat{\delta}n(\alpha{i+1}, \dots, \alpha_{n-1}, x) C(r, X, x)$$ 这两个函数之间的关系是: $$v_i(X) = vi'(X) \cdot \hat{\delta}{i+1}((\alpha_0, \dots, \alphai), (r, X))$$ 其中 $\hat{\delta}{i+1}$ 因为验证者拥有 $\alpha$ 和 $r$,所以是完全已知的。这个修改的好处在于 $v_i'(X)$ 的次数比 $v_i(X)$ 少 1,这意味着证明者需要评估的点更少。因此,主要的协议变化发生在轮次之间的检查环节。
此外,将原本的约束$vi = v{i+1}(0) + v_{i+1}(1)$ 优化为: $(1 - \alphai)v{i+1}'(0) + \alphai v{i+1}'(1) = vi'(X)$。 则证明者需要评估和发送的数据更少,进一步减少传输的数据量。 计算$\hat{\delta}{n-i-1}$ 也比计算$\hat{\delta}_n$更高效。 通过这两项改进,成本降低为大约: $2^{n-1}(d - 1)C_F + 2^{n-1}dC_G$。 在常见的 $d = 3$ 情况下,这些优化使成本降低了 5/3 倍。
3. 代数插值优化 对于诚实的证明者,$C(x0, \dots, x{n-1})$在$H_n$上为零,可表示为: $$C(x0, \dots, x{n-1}) = \sum_{i=0}^{n-1} x_i(x_i - 1) Q_i(x0, \dots, x{n-1})$$ 虽然$Q_i$不是唯一的,但可以通过多项式长除法构造一个有序的分解:从 $R_n = C$ 开始,逐次除以 $x_i(x_i - 1)$ 来计算 $Q_i$ 和 $R_i$,其中 $R_0$ 是 $C$ 在 $H_n$ 上的多线性扩展,且假设其为零。
分析 $Q_i$ 的次数,可以得出:对于 $j > i$,$Q_j$ 在 $x_i$ 上的次数与 $C$ 相同;对于 $j = i$,次数减少 2;对于 $j < i$,次数至多为 1。
给定向量 $r = (r_0, \dots, r_i)$,$Q_j(r, X)$ 对于所有 $j \leq i$ 都是多线性的。 此外$Qi(r, X) = \sum{j=0}^{i} r_j(r_j - 1) Qj(r, X)$是与$C(r, X)$ 在 $H{n-i}$上相等的唯一多线性多项式。对于任何$X$和$x \in H_{n-i-1}$,可以表示为: $$C(r, X, x) - Qi(r, X, x) = X(X - 1) Q{i+1}(r, X, x)$$ 因此,在协议的每一轮中,仅引入一个新的$Q$,其评估值可以从$C$和先前的$Q$计算得出,实现插值优化。
3.3 Sumcheck PIOP优化:基于小域的Sumcheck协议
Binius所实现的STARKs方案,其承诺开销很低,使得prover瓶颈不再是PCS,而在于sum-check协议。
Ingonyama在2024年提出了针对基于小域的Sumcheck协议的改进方案(对应图3中的Algo 3和Algo 4算法),并开源了实现代码。算法4专注于将Karatsub算法合并到算法3中,以额外的基域乘法为代价来最小化扩域乘法次数,因此当扩域乘法比基域乘法昂贵得多时,算法4的性能会更好。
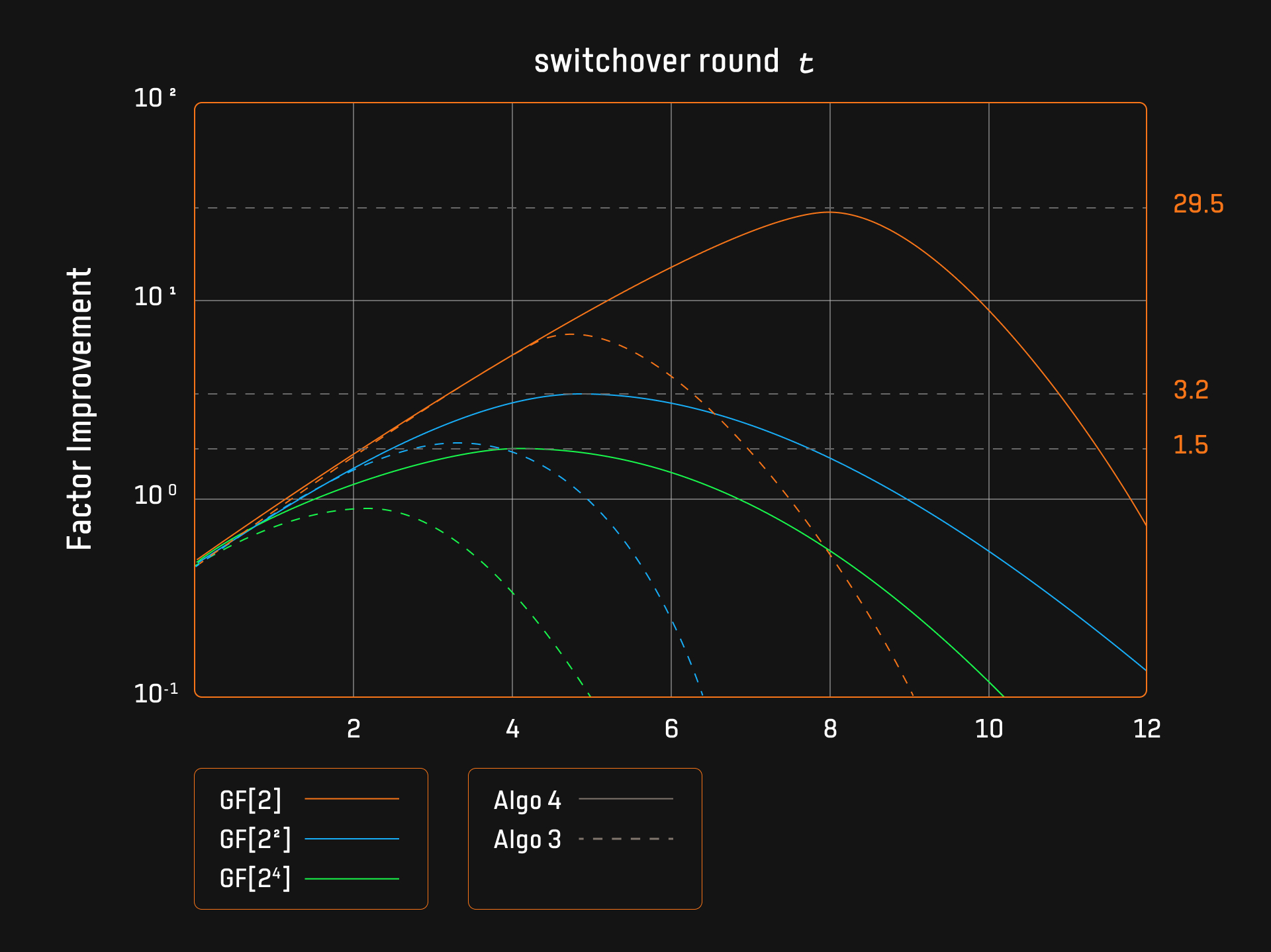
1. 切换轮次的影响与改进因子: 基于小域的Sumcheck协议的改进集中于切换轮次$t$的选择。切换轮次是指从优化算法切换回朴素算法的时间点,论文的实验表明,在最佳切换点时,改进因子达到最大值,随后呈现抛物线趋势。如果超过这一切换点,优化算法的性能优势减弱,效率下降。这是由于小域上的基域乘法与扩域乘法相比有更高的时间比率,因此在适当时机切换回朴素算法至关重要。
对于具体应用,如涉及Cubic Sumcheck($d=3$)的情况,基于小域的Sumcheck协议相较于朴素算法的改进达到了一个数量级。例如,在基域为$GF[2]$的情况下,算法4的性能比朴素算法高出近30倍。
2. 基域大小对性能的影响: 论文的实验结果表明,较小的基域(如$GF[2]$)能够使优化算法显示出更显著的优势。这是因为扩展域与基域乘法的时间比率在较小基域上更高,从而优化算法在此条件下表现出更高的改进因子。
3. Karatsuba算法的优化收益: Karatsuba算法在提升基于小域的Sumcheck性能方面表现出显著的效果。对于基域$GF[2]$,算法3和算法4的峰值改进因子分别为6和30,表明算法4比算法3高效五倍。Karatsuba优化不仅提升了运行效率,也优化了算法的切换点,分别在算法3的$t=5$和算法4的$t=8$达到最佳。
4. 内存效率的提升: 基于小域的Sumcheck协议除了提升运行时间,还在内存效率方面表现出显著的优势。算法4的内存需求为$O(d \cdot t)$,而算法3的内存需求为$O(2^d \cdot t)$。当$t=8$时,算法4仅需0.26MB的内存,而算法3则需67MB来存储基域的乘积。这使得算法4在内存受限设备上表现出更强的适应性,尤其适用于资源有限的客户端证明环境。
3.4 PCS优化:FRI-Binius降低Binius proof size
Binius协议的一个主要缺陷在于其相对较大的证明大小,随着见证大小的平方根按$O(\sqrt{N})$缩放。与更高效的系统相比,这种平方根大小的证明是一种局限性。相反,对数级(polylogarithmic)证明大小对于实现真正“简洁”的验证器至关重要,这在像Plonky3这样的先进系统中得到了验证,后者通过FRI等先进技术实现了对数级证明。
论文《Polylogarithmic Proofs for Multilinears over Binary Towers》,简称为FRI-Binius,实现了二进制域FRI折叠机制,带来4个方面的创新:
- 扁平化多项式: 初始的多线性多项式被转换为LCH(低码高度)新颖多项式基。
- 子空间消失多项式: 用于在系数域上执行FRI,并通过加性NTT(数论变换)实现类似FFT的分解。
- 代数基打包: 支持协议中信息的高效打包,可移除嵌入开销。
- 环交换SumCheck: 一种新颖的SumCheck方法,利用环交换技术优化性能。
基于二进制域FRI-Binius的多线性多项式承诺方案(PCS)的核心思想为:FRI-Binius协议通过将初始的二进制域多线性多项式(定义于$\mathbb{F}_2$上)打包为定义在更大域$K$上的多线性多项式来操作。
在基于二进制域的FRI-Binius PCS中,过程如下:
- 承诺阶段: 对一个$\ell$变量的多线性多项式(定义于$\mathbb{F}2$上)的承诺被转化为对一个打包后的$\ell'$变量的多线性多项式(定义于$\mathbb{F}{2^{128}}$上)的承诺,系数个数因此减少了128倍。
- 评估阶段: 证明方和验证方进行$\ell'$轮交叉环切换SumCheck和FRI交互证明(IOPP):
- FRI开放证明占据了证明大小的大部分。
- 证明方的SumCheck成本类似于常规大域上的SumCheck成本。
- 证明方的FRI成本与常规大域上的FRI成本相同。
- 验证方接收128个来自$\mathbb{F}_{2^{128}}$的元素,并执行128个额外的乘法运算。
借助FRI-Binius,可将Binius证明大小减少一个数量级。这使得Binius的证明大小更加接近最先进的系统,同时保持与二进制域的兼容性。专为二进制域定制的FRI折叠技术,加上代数打包和SumCheck的优化,使得Binius能够在保持高效验证的同时,生成更加简洁的证明。
| 表 4: Binius与FRI-Binius证明大小对比 | Total Data Size | Coeff. Size | Packing Factor | Binius Proof Size (MiB) | FRI-Binius Proof Size (MiB) |
|---|---|---|---|---|---|
| 512MB (2^32 bits) | 6 | 0 | 2.7 | 0.55 | |
| 3 | 2 | 5.4 | 0.95 | ||
| 0 | 4 | 10.8 | 3.51 | ||
| 8.192GiB (2^36 bits) | 6 | 0 | 10.8 | 0.74 | |
| 3 | 2 | 21.6 | 1.28 | ||
| 0 | 5 | 59.1 | 4.58 |
| 表 5: Plonky3 FRI与FRI-Binius对比 | Scheme | Coeff. Bits | Current Size (MiB) | Optimized Size (MiB) | Commit + Prove Time (s) |
|---|---|---|---|---|---|
| Plonky3 FRI | 31 | 1.1 | 0.31 | 9.55 | |
| FRI-Binius | 1 | 0.84 | 0.16 | 0.91 | |
| 8 | 1.09 | 0.20 | 7.6 | ||
| 32 | 1.29 | 0.24 | 28.9 |
4. 小结
Binius的整个价值主张是,可为witnesses使用最小的power-of-two域,因此只需根据所需来选择域大小。Binius是“使用硬件、软件、与FPGA中加速的Sumcheck协议” 的协同设计方案,可以以非常低的内存使用率来快速证明。
Halo2和Plonky3等证明系统有4个占用大部分计算量的关键步骤:生成witness数据、对witness数据进行承诺、vanishing argument、opening proof。
以Plonky3中的Keccak和Binius中的Grøstl哈希函数为例,二者对应的以上4大关键步骤计算量占比情况如图3所示:
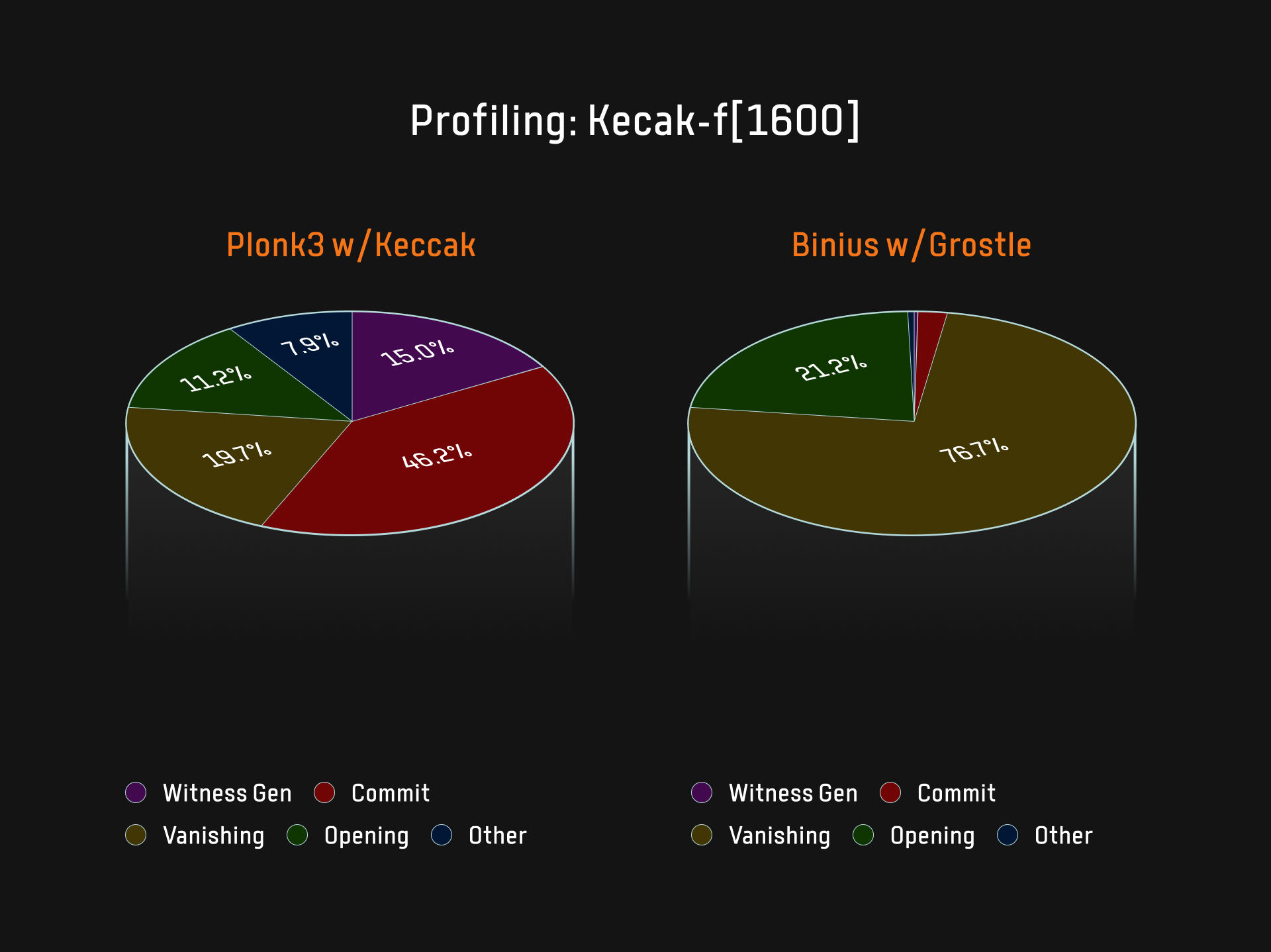
由此可知,Binius中已基本完全移除了Prover的commit承诺瓶颈,新的瓶颈在于Sumcheck协议,而Sumcheck协议中大量多项式evaluations和域乘法等问题,可借助专用硬件高效解决。
FRI-Binius方案,为FRI变体,可提供一个非常有吸引力的选择——从域证明层中消除嵌入开销,而不会导致聚合证明层的成本激增。
当前,Irreducible团队正在开发其递归层,并宣布与Polygon团队合作构建Binius-based zkVM; Jolt zkVM正从Lasso转向Binius,以改进其递归性能; Ingonyama团队正在实现FPGA版本的Binius。
参考文献
- [2024.04 Binius Succinct Arguments over Towers of Binary Fields](https://eprint.iacr.org/2023/1784
- 2024.07 Fri-Binius Polylogarithmic Proofs for Multilinears over Binary Towers
- 2024.08 Integer Multiplication in Binius: GKR-based approach
- 2024.06 zkStudyClub - FRI-Binius: Polylogarithmic Proofs for Multilinears over Binary Towers
- 2024.04 ZK11: Binius: a Hardware-Optimized SNARK - Jim Posen
- 2023.12 Episode 303: A Dive into Binius with Ulvetanna
- 2024.09 Designing high-performance zkVMs
- 2024.07 Sumcheck and Open-Binius
- 2024.04 Binius: highly efficient proofs over binary fields
- 2023.12 SNARKs on binary fields: Binius - Part 1
- 2024.06 SNARKs on binary fields: Binius - Part 2
- 2022.10 HyperPlonk, a zk-proof system for ZKEVMs
- lambdaworks 2026 年更新路线图和优先级 346 浏览
- op succint(op Kailua等riscv通用零知识证明虚拟机)和zkysnc等专用零知识证明的在以太坊上面的核心区别 480 浏览
- 从零开始构建 ZK (STARK) 证明器的旅程 906 浏览
- 区块链扩容 1871 浏览
- ZK Rollup 开发公司:构建可扩展、私密和高速的 Web3 解决方案 638 浏览
- 零知识证据,给 Cashu 带来任意的花费条件 752 浏览
- ZK/SEC季度报告 642 浏览
- ZK/SEC 季度报告 551 浏览
- Succinct Labs:SP1和SPN有什么区别? 1626 浏览
- 以太坊扩容方案:状态通道、Plasma、Rollup 1667 浏览
- 012:L2 是什么?Rollup 到底 Roll 的是什么? 2241 浏览
- Circle STARKs:第三部分,Circle FFT - ZKSecurity 2284 浏览

