zkMIPS解读
【zkMIPS系列】zkVM概述
- ZKM
- 发布于 2024-12-05 20:15
- 阅读 2313
zkVM(零知识虚拟机)是一种利用零知识证明(ZKP)来保证计算的正确性、完整性和隐私性的虚拟机。
zkVM
zkVM(零知识虚拟机)是一种利用零知识证明(ZKP)来保证计算的正确性、完整性和隐私性的虚拟机。
1. 预备知识
1.1 概念
- 零知识证明:证明方(prover)向验证方(verifier)证明某个陈述是真实的,同时不向验证方传递除该陈述真实性之外的任何信息。 包括以下4个性质:
- 零知识性
- 简洁性
- 非交互性
- 透明性
- 有效性证明
- 用于证明状态转换的有效性。例如,zk-Rollups 使用有效性证明来向父链证明状态转换的合法性,通常与 SNARKs 和 STARKs 等证明系统配合使用。
- 欺诈证明
- 用于验证方挑战交易的有效性。
- 可验证计算
- 允许客户端将函数 $F$ 的计算任务外包给不可信的工作方,并验证返回结果的正确性。
1.2 电路与门
编写一个 ZKP 应用时,需要经过以下三个步骤:
- 用一种语言定义问题(约束满足问题)
| 名称 | 核心贡献者 | 主要特性 | 应用场景 |
|---|---|---|---|
| Circom/SnarkJS | Iden3 | 易学,最广泛使用的 DSL(领域专用语言),优化电路创建;Circom 主要兼容广泛使用的 ZKP 系统,如 snarkjs 和 libsnark | Dark Forest 和 Tornado Cash |
| Zokrate | Jacob Eberhardt 和 Alex Gluchowski,达姆施塔特工业大学 | ZoKrates 是一个基于以太坊的 zkSNARK 工具箱;类似 Python 的编程语言 | |
| SnarkyJS | O(1) Labs | 支持开发者创建合约,基于 Node.js 和浏览器兼容性等成熟技术 | Mina 协议上的 zkApps |
| Cairo | Starkware | 专注于安全性和易用性,支持开发 StarkNet 智能合约 | StarkNet 和 StarkEx |
| Noir | Aztec | 提供隐私保护功能,支持多种证明系统 | 仍在开发中 |
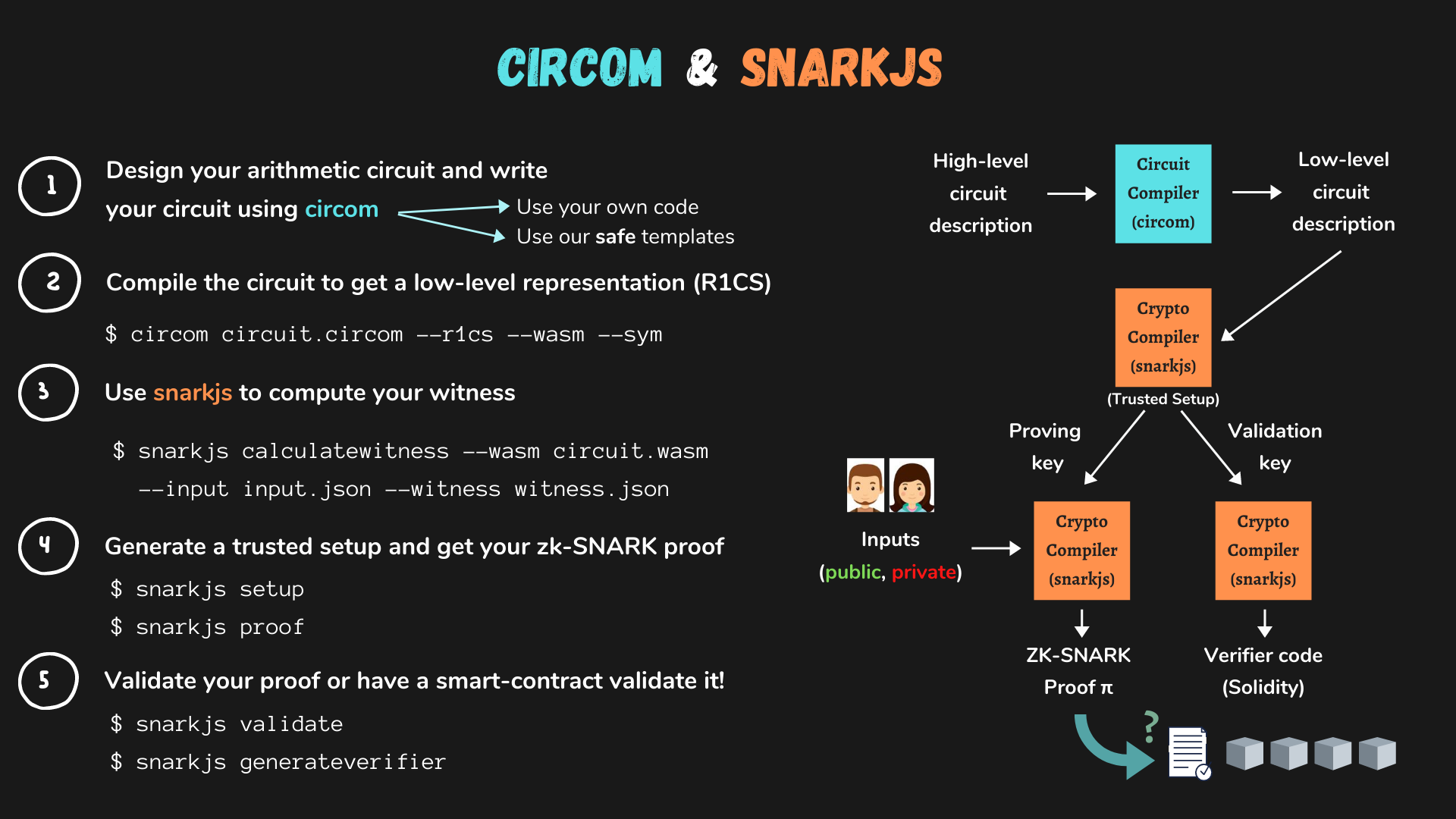
以下是如何使用 Circom 实现一个乘法器的示例。
Multiplier2.circom:
pragma circom 2.0.0;
/*该电路模板检查 c 是否为 a 和 b 的乘积。*/
template Multiplier2 () {
// 信号声明
signal input a;
signal input b;
signal output c;
// 约束
c <== a * b;
}流程图如下:
-
算术化 (Arithmetization):将程序转换为一组多项式
-
电路计算: 该方法将程序降至门级(Gate Level)的概念层面。然而,这里的门并非处理器中的物理门,而是逻辑上的概念门。
- R1CS:最大多项式次数为 2,满足以下方程: $$ \left( \sumk A{ik} z_k \right)\left( \sumk B{ik} z_k \right) - \left( \sumk C{ik} z_k \right) = 0 $$
其中 $A{ik}, B{ik}, C_{ik}$ 是某有限域 $F$ 中的元素。例如,给定表达式 $y = x^3$,可通过引入中间变量如下表达:
$$ x \cdot x = w_1\ w_1 \cdot w_1 = w $$
中间变量可以是电路的私有/公共输入。需要注意,描述计算的 R1CS 表示法并不唯一。例如,上述表达式还可以表示为:
$$ x \cdot x = w_1 \ w_1 \cdot x = w_2 \ w_2 \cdot x = w $$
- Plonkish:支持双输入门(two fan-in gates),允许实现自定义门(Custom Gate)。
$$ q_L x_a + q_R x_b + q_O x_c + q_M x_a x_b + q_C = 0 $$
其中 $q_L, q_R, q_O, q_M, q_C$ 是选择操作的控制参数,用于表示 R1CS 的操作。
-
计算机计算:
该方法与计算机工作原理类似,包括一组寄存器和修改寄存器值的状态转换函数。- AIR 和 PAIR:适用于均匀计算。
-

- [**CCS (Customizable Constraint System)**](https://eprint.iacr.org/2023/552):
CCS(可定制约束系统)是一种通用的约束表示方法,同时支持 R1CS、Plonkish 和 AIR。
- **简单对比** 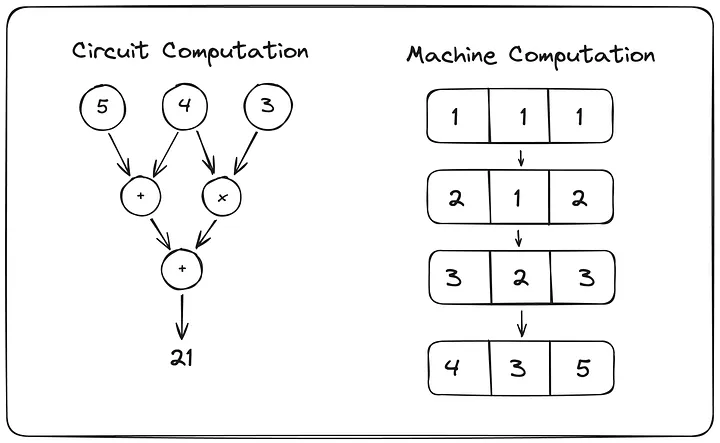
-
定义证明者实例,生成证明及验证者
-
交互式 Oracle 证明(IOP):
IOP 是一种交互证明协议,其中验证者无需读取证明者的整个消息,而是可以通过 Oracle 访问所需的任意符号,这样使得验证者的运行时间可以低于证明总长度(即所有消息长度之和)。 -
多项式承诺方案(Polynomial Commitment Scheme):
一种密码协议,用于承诺多项式并在后续验证特定点的评估值,避免证明者将整个见证 $w$ 发送给验证者。一般交互式协议流程如下:
- 证明者承诺一个或多个多项式,使用指定的多项式承诺方案。
- 验证者随机选择一个或多个域元素,将其作为挑战逐一发送给证明者,并请求证明者提供所承诺多项式在这些随机选定点的评估值(称为开放值)。
- 此“问答”交互可以根据验证者要求的开放次数重复进行,以确保证明的可靠性。
- 验证者使用相关的多项式约束测试证明者的开放值的真实性。
通过 Fiat-Shamir 方法可以将交互式协议转换为非交互式协议。
-
KZG 承诺方案:
-
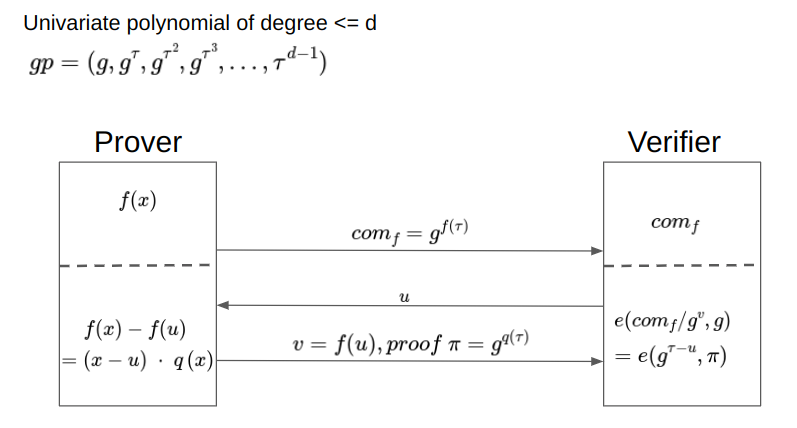
来源:[https://youtu.be/xuGQYEvytxk?t=640](https://youtu.be/xuGQYEvytxk?t=640)
- **FRI 承诺方案**(如 [eSTARK](https://eprint.iacr.org/2023/474.pdf)): 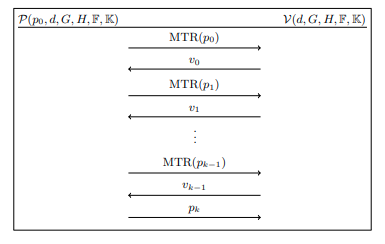
**提交阶段**
证明者 $\mathcal{P}$ 在乘法子群 $H$ 上提交多项式 $p_0$。多项式的度数为 $d$,所有元素来自域 $F$,$G$ 是域 $F$ 的生成元,$K$ 是 $H$ 的扩展域。
MTR 是默克尔树的根节点。验证者随机生成一个值并将其发送给证明者,证明者将 MTR 提交给验证者作为开放值。 
-
证明系统:
- Groth16:如 rapidsnark, libsnark, arkworks
- Plonk:如 Bellman, Halo2
- EthStark
-
发布验证者到链上:
- 选择合适的链上椭圆曲线:如 BN128, BLS12381
问题: 我们是否可以使用高级语言(如 Golang、Rust)定义问题模型?
2. zkVM 深入剖析
2.1 概览
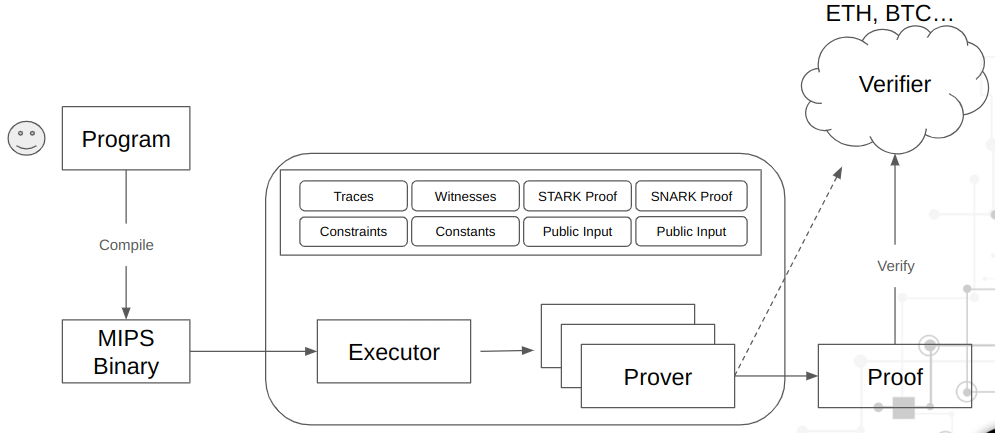
2.2 虚拟机 (Virtual Machine)
在计算领域,虚拟机(VM)是计算机系统的虚拟化或仿真。虚拟机基于计算机体系结构,提供类似物理计算机的功能。
计算机体系结构是对计算机系统由组成部分(如 CPU、内存、ALU 等)构成的结构的描述。
2.2.1 两种主要架构
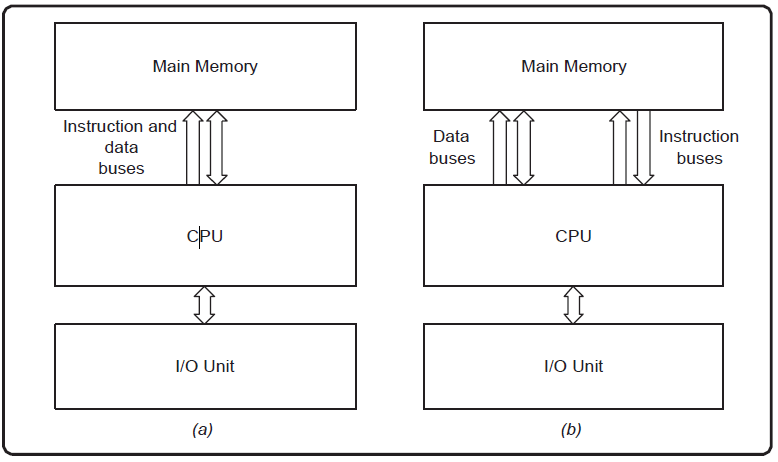
- CPU
- 内存
- 寄存器
- 总线
- 输入/输出单元
2.2.2 RISC 指令集架构 (ISA)
RISC(精简指令集计算机)旨在简化计算机执行任务时的指令集合。
以下是 MIPS32 中 ADDI 指令的示例,该指令允许选择源寄存器和目标寄存器,并包含一个小的常数。
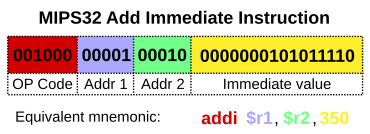
在 zkVM 中,有三种主要的 RISC ISA:
- MIPS
- RISC V
- WASM
其中,RISC V 更像是简化版的 MIPS。

来源:第 322 页,《计算机组成与设计:硬件/软件接口——RISC-V 版》
2.3 实现一个简易 zkVM:菲波那切执行器
2.3.1 生成执行轨迹
基于现有的知识,我们可以实现一个简易 zkVM,例如菲波那切执行器,用于计算斐波那契序列的第 n 项。
$$ f(n) = f(n-1) + f(n-2) \ f(0) = f(1) = 1 $$
选择 AIR(代数中间表示)作为代数化方法。
定义一个状态机 $S$,包含如下两个变量,并设 $i$ 为域大小:
$$ S = (A_i, Bi) \ S' = (A{i+1}, B_{i+1}) $$
现在可以使用状态机 $S$ 表示菲波那切执行器:
$$ A_{i+1} = Bi \ B{i+1} = A_i + B_i $$
因此,对于域中的所有 $i$,执行轨迹表如下,设 $n = 6$:
| 计数器 | A | B |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 1 | 2 |
| 2 | 2 | 3 |
| 3 | 3 | 5 |
| 4 | 5 | 8 |
| 5 | 8 | 13 |
2.3.2 构建多项式等式
在虚拟机中,每个状态使用一个寄存器表示。
用于表示两个寄存器的多项式来自于多项式集 $F_p[X]$ ,其中系数是素数域 $F_p$ 中的元素,且 $p = 2^{64} - 2^{32} + 1$ 。
因此,上述域是一个子群:
$$ H = {\omega_0, \omega_1, \omega_2, \ldots, \omega_d=\omega_0 } \subset F_p^d $$
定义两个多项式 $P(X)$ 和 $Q(X)$ 来表示轨迹列 $A$ 和 $B$ :
$$ P(\omega^i) = A_i \ Q(\omega^i) = B_i $$
显然可以看出:
$$ P(\omega^i \cdot \omega) = P(\omega^{i+1}) = A{i+1} \ Q(\omega^{i} \cdot \omega) = Q(\omega^{i+1}) = B{i+1} $$
利用拉格朗日插值,我们可以计算出 $P$ 和 $Q$ 的系数形式。
现在可以使用多项式约束来限制具有两个寄存器的状态转换:
$$ P(X \cdot \omega) = \bigg|_H Q(X) \ Q(X \cdot \omega) = \bigg|_H P(X) + Q(X) $$
2.3.3 引入循环性
由于 $H$ 是一个子群,因此:
$$ P(\omega^5 \cdot \omega) = \bigg|_H Q(\omega^5) = 13, \ P(\omega^5 \cdot \omega) = P(\omega^0) = 1 $$
显然,在最后一行中约束被破坏。
解决方案是引入另一个寄存器 $LAST$ 来标记最后一行,并为其分配一个向量值 $[0, \ldots, 1]$ 。轨迹表变为:
$$ P(X \cdot \omega) = \bigg|_H Q(X) \cdot (1 - LAST(X)) + LAST(X) \cdot P(\omega^0) \ Q(X \cdot \omega) = \bigg|_H (P(X) + Q(X)) \cdot (1 - LAST(X)) + LAST(X) \cdot Q(\omega^0) $$
总结来说,状态机中有两种基本约束类型:
- 状态转换约束:如寄存器 $P$ 和 $Q$
- 边界约束:如寄存器$LAST$
在实际的 zkVM 开发中,有各种指令类型,例如算术、逻辑、分支/跳转和内存等。每条指令只需少量状态来表示,但一个程序可能需要数千个状态。
以下是 zkMIPS 实现的概览:
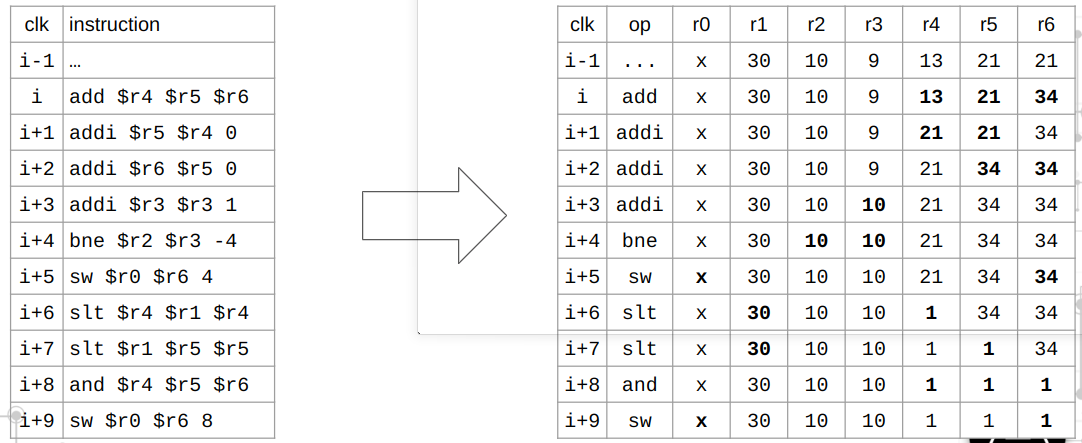

2.3.4 多项式承诺
现在可以将上述约束转换为多项式等式:
$$ P_0 = (1 - LAST(X)) \cdot (P(X \cdot \omega) - Q(X)) = 0 \ P_1 = (1 - LAST(X)) \cdot (Q(X \cdot \omega) - (P(X) + Q(X))) = 0 $$
基于多项式等式的证明系统利用了Schwartz-Zippel 引理的基本属性。
根据 Schwartz-Zippel 引理,对于来自验证者的随机挑战 ${\alpha_1, \alpha_2, \ldots, \alpha_l}$ ,证明者找到一个虚假的多项式 $Q^\prime$ (其次数为 $d$ )的概率,满足:
$$ Q^\prime(\alpha_j) = Q(\alpha_j) \quad \text{对于所有 } j \in {1, 2, \ldots, l} $$
该概率最多为 $\frac{d}{|S|}$ ,这是可以忽略的。
定义 $z_H(X)$ 为消失多项式,计算商多项式 $q_i(X)$ :
$$ P_0 = (1 - LAST(X)) \cdot (P(X \cdot \omega) - Q(X)) = z_H(X) \cdot q_1(X) \ P_1 = (1 - LAST(X)) \cdot (Q(X \cdot \omega) - (P(X) + Q(X))) = z_H(X) \cdot q_2(X) $$
因此,我们可以使用多项式承诺方案(如 FRI 或 KZG)来承诺轨迹和商多项式 $R_i, q_i(X)$。
3. 通用 zkVM 设计理念
通常来说,有三种主要的zkVM:
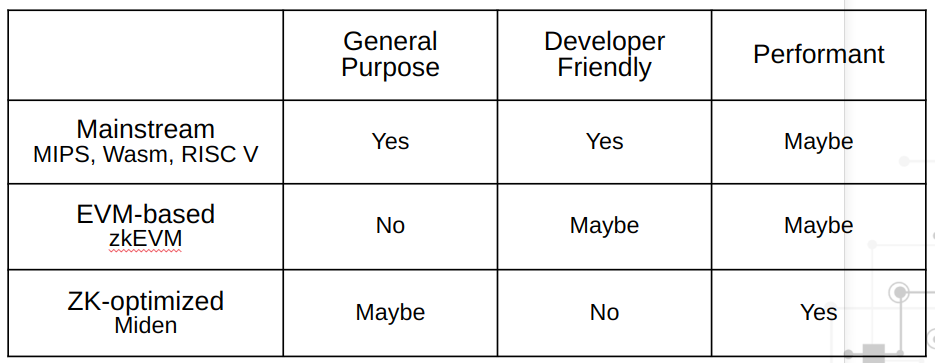
4. 通用技术
4.1 主机与子机
- 在现代指令集架构(ISA)中,虚拟机由不同的组件组成,如 CPU、ALU、内存、输入/输出、总线以及其他外设。
- 不同的组件处理不同的指令,并通过总线进行通信。
以 zkMIPS 为例,我们实现了62条指令,并将所有指令分类为以下几类:
- 算术和算术立即数:如 ADD, ADDI 等
- 逻辑和逻辑立即数:如 AND, ANDI 等
- 移位和移位立即数:如 SLL, SLLV 等
- 加载和存储:如 LB, SB 等
- 跳转/偏移跳转/分支:如 JUMP, JUMPI 等
- 系统调用:如 Read, Write 等
因此,如果我们使用单个轨迹表,并将所有状态变量都放入其中,表格将变得非常大且稀疏(即表中存在大量的0值单元)。这会导致以下问题:
- 列数非常大 ⇒ 需要承诺的轨迹多项式数量很多
- 行数非常大 ⇒ 域大小非常大,轨迹多项式的次数也非常高
这两点都会导致多项式承诺方案(PCS)中的计算量非常大。
一种常见的优化方法是将大的表格拆分成多个子表格,如下所示:
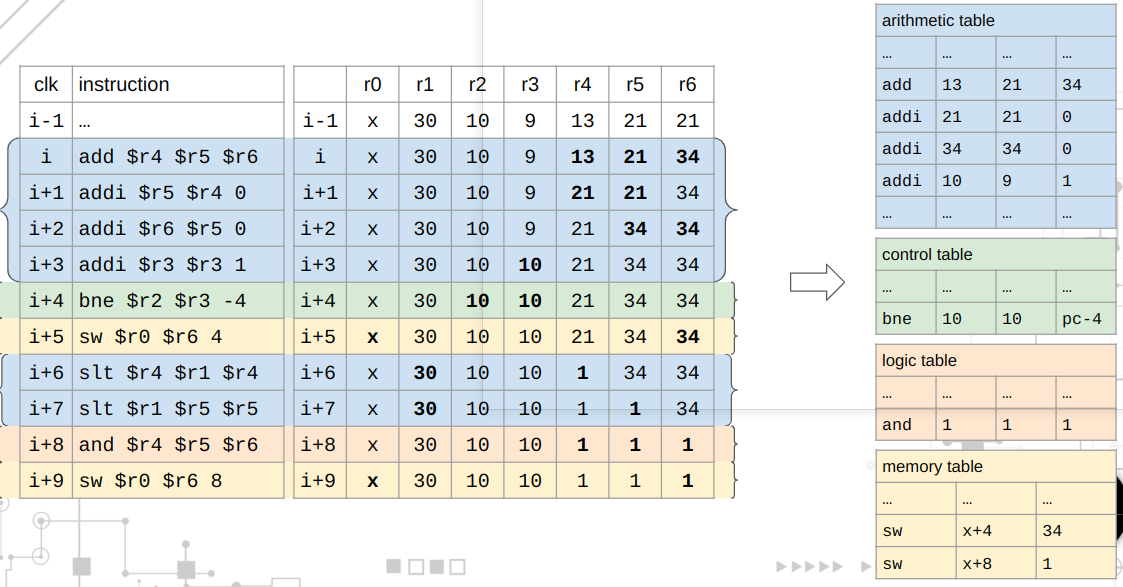
这种拆分带来了其他工程上的好处:
- 更小的内存和 CPU 消耗
- 支持并行证明
- 模块化:不同的工程师可以专注于不同电路的实现和优化
4.2 查找方案
查找参数(Lookup arguments)允许证明提交的向量元素来自另一个(更大的)提交表。这种方案常用于实现 zkVM 中的通信总线。从广义上讲,这些协议可以用来证明如下形式的陈述:
- 给定一个表 $T={t_i}, i=0,\ldots,N-1$ ,其中所有值互不相同(称为“行”),
- 以及一个查找列表 $F={f_j}, j=0,\ldots,m-1$ (其中值可能重复出现),
- 所有查找值均包含在表中,即 $F \subseteq T$ 。
在这一框架中,表 $T$ 通常被认为是公开的,而查找列表 $F$ 被视为私有证据。可以将表 $T$ 理解为存储某个变量的所有合法值,而查找列表 $F$ 则是执行特定程序时生成的该变量的具体实例。被证明的陈述表明,在程序执行过程中,该变量始终保持在合法范围内。
在此讨论中,我们假设 $m < N$ ,且通常 $m \ll N$ (除非另有说明)。我们将回顾查找协议的演变与种类,并探索证明这类陈述的多种应用。
在深入查找方案之前,让我们先通过多重集相等性(Multiset equality)来检查一个置换参数:
$$ \prod_i (X - f_i) = \prod_j (X - t_j) $$
其中 $X$ 属于域 $\mathbb{F}$ 。我们可以选择一个随机数 $\alpha\in \mathbb{F}$ ,并将上述多项式等式检查简化为一个大积(grand product)。
此外,如果 $F \subseteq T$ ,则存在 $m_j$ ,使得:
$$ \prod_i (X - f_i) = \prod_j (X - t_j)^{m_j} $$
特别地,如果所有 $m_j$ 都为 1,则我们有一个多重集相等性问题。这看起来问题已经解决,但计算复杂度与集合 $T$ 的大小有关,而 $T$ 的大小可能非常大。
现在让我们深入了解查找方案的历史。
4.3 查找参数方案
Plookup
Plookup 是最早的查找协议之一。证明者的计算复杂度为 $O(N \log N)$ 个域运算,该协议可以推广以支持多表查找和向量查找。其过程包括对向量 $f$ 和表 $t$ 的元素按升序排序,并定义:
$$ {(sk, s{k+1})} = {(tj, t{j+1})} \cup {(fi, f{i+1})} $$
作为多重集(multisets),然后进行以下检查:
$$ \prod_k (X + sk + Y \cdot s{k+1}) = \prod_i (X + fi + Y \cdot f{i+1}) \prod_j (X + tj + Y \cdot t{j+1}) $$
其中 $X$ 和 $Y$ 属于域 $\mathbb{F}$ 。
此协议可以通过大积(grand product)再次简化计算。
4.3.1 Caulk
Caulk 使证明者的工作量依赖于 $C_m$ 的大小 $m$ ,而不是 $C$ 的大小 $N$ 。证明者通过识别一个子集 $C_I$ (包含 $C_m$ 的元素)并使用 KZG 承诺证明 $C - C_I = Z_I(x) \cdot H_I(x)$ 。此协议具有子线性效率,证明者的计算复杂度为 $O(m \log N)$ 。
4.3.2 Caulk+
Caulk+ 是 Caulk 的改进版本,通过更高效的整除性检查进一步降低了证明者的计算复杂度。该协议通过计算多项式 $Z_I$ 、 $C_I$ 和 $U$ 来证明 $Z_I$ 可以整除 $C - C_I$ 和 $X^n - 1$ 。同时通过引入模糊因子(blinding factors)保持零知识特性,将证明者的计算复杂度降低至 $O(m^2)$ 。
4.3.3 Baloo
Baloo 扩展了 Caulk+,通过对表子集进行消失多项式形式的承诺,并在子集大小上实现准线性时间。它引入了一种“承诺与证明”(commit and prove)协议,并采用通用的 Sumcheck 协议将证明归约为内积参数(inner product argument)。该协议高效并支持多列查找,在 zkEVM 等 SNARK 中具有广泛应用前景。
4.3.4 Flookup
Flookup 被设计用于高效地证明提交多项式的值属于一个大表。该协议利用配对(pairing)提取相关表子集的消失多项式,并引入了一种新的多项式交互证明(IOP)。在经过 $O(N \log^2 N)$ 的预处理后,证明者以准线性时间 $O(m \log^2 m)$ 运行,大幅改进了之前的二次计算复杂度,特别适用于大域上的 SNARK 证明。
4.3.5 cq
cq 使用对数导数方法将成员资格证明简化为有理多项式等式检查。通过对商多项式的“缓存商”(cached quotients)进行预计算,协议使表项的计算更加高效。证明者时间为 $O(N \log N)$ ,证明大小为 $O(N)$ ,效率超过了 Baloo 和 Flookup,同时保持同态等特性。
4.3.6 LogUp
LogUp 高效地证明了一组见证值存在于布尔超立方体查找表中。通过使用对数导数,该方法将集合包含问题转换为有理函数等式检查,仅要求证明者提供一个重数函数。LogUp 比多变量 Plookup 变体更高效,需要的 Oracle 承诺次数减少 3-4 倍。对于大批量查找,它的效率也优于 Plookup 的有界重数优化。该方法适用于向量值查找,且可扩展用于范围证明,对 SNARK(如 PLONK 和 Aurora)及应用(如 tinyRAM 和 zkEVM)尤为重要。
4.4 证明聚合与递归
聚合是生成每个区块的单独证明并将它们组合成另一个证明的最简单方法。第一类证明验证“区块是有效且已上链”,第二类证明验证“所有这些区块证明是有效的”。这种方法称为聚合(aggregation)。
在聚合方案中,第二个电路只能在所有区块证明准备就绪后开始聚合。然而,如果我们能够逐块处理呢?这就是递归所做的。
在递归方案中,每个区块证明验证两件事:当前区块有效,以及前一个证明有效。一个证明“包裹”了前一个证明,整体结构类似于链条。
以 zkMIPS 的递归证明为例:
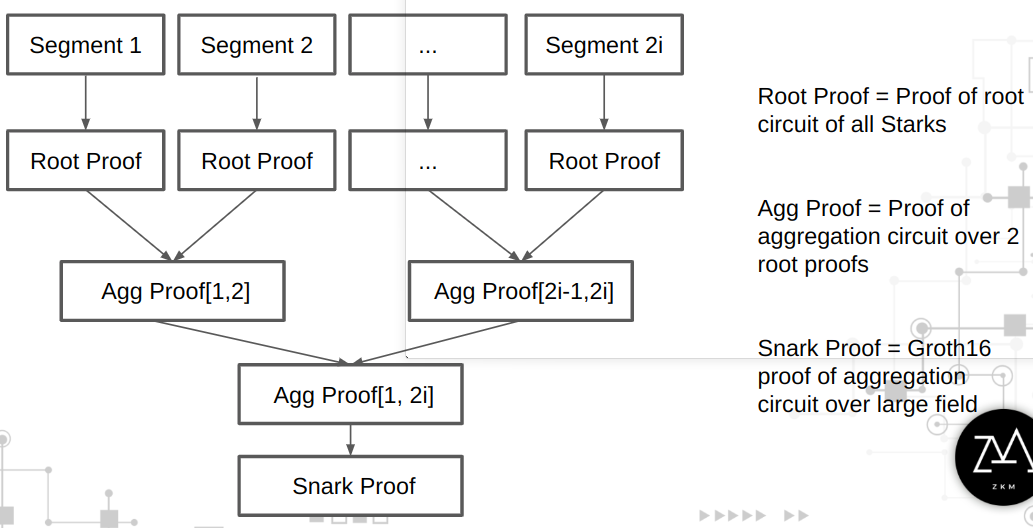
4.5 延续性机制(Continuation)
- 延续性是一种机制,用于将一个大型程序拆分为若干较小的段,这些段可以独立执行并证明。这种机制提供以下优势:
- 并行生成证明
- 在 zkVM 中启用检查点功能
- 将内存需求限制为固定大小,无论程序规模如何
- 段(Segment):
一个段是由 MIPS 轨迹组成的序列,具有入口 PC 和图像 ID。 - 内存一致性检查(Check Memory Consistent)
4.6 zkVM 示例
| 系统 | 证明系统 | ISA | 编译器 | 编程语言 |
|---|---|---|---|---|
| zkMIPS | Plonky2 | MIPS | Rust 编译器 / Golang 编译器 | Rust, Golang |
| RISCZero | STARKs | RISC V | Rust 编译器 | Rust |
| SP1 | Plonky3 | RISC V | Rust 预编译器 | Rust |
| Starknet | STARKs | Cario | 专有编译器 | Cario |
| zkWASM | Halo2 | WASM | Rust 编译器 | Rust |
| Polygon Miden | STARKs | Miden ASM | 专有编译器 | 支持 Miden 的 Rust SDK |
4.7 zkVM评估
效率
为了估算为程序 $P$ 生成证明所需的时间,我们需要考虑:
- 程序 $P$ 中的指令数量
- 约束复杂度
并使用以下公式计算 ISA 的效率:
$$ #\ 指令数 \times \frac{\text{约束复杂度}}{\text{每条指令}} \times \frac{\text{时间}}{\text{约束复杂度}} $$
来源: 视频链接
评估 zkVM 性能的方法:
- 测试场景:SHA2、SHA3、Rust EVM、Rust Tendermint 等。
- 指标:
- 每秒证明周期数(Proving cycles per second 或 HZ)
- 每 gas 的证明能耗(Proving energy cost per gas)
开源框架:
包含 RISCZero、zkMIPS、SP1 和 Jolt,可参考 zkMIPS/zkvm-benchmarks。
4.7.2 开发工具链
zkVM 应提供对开发者友好的工具链,允许开发者构建、编译其程序并将验证器部署到链上。
正确性
- VM 必须按照预期执行程序。
- 证明系统必须满足其声明的安全属性,例如:
- 健全性(Soundness)
- 完备性(Completeness)
- 零知识性(Zero Knowledge)
简洁性
- zkVM 生成的证明应可在链上验证。
- 较小的证明大小、较短的验证时间以及透明设置是优良特性。
4.8 应用场景
-
混合 Rollup:Optimistic + ZK
Metis 将 Optimistic Rollups 的灵活性和可组合性与 zkMIPS 的可扩展性相结合,形成一个统一协议,将最终确认时间从 7 天减少到不足 1 小时。 -
比特币 L2:
GOAT 网络实现了基于 zkMIPS 的 BitVM2 协议,构建了一个在安全性上无任何妥协的真实比特币 L2。 -
zk 身份验证(zkIdentity)
-
zk 机器学习(zkML)
 来源:
来源: