从零开始学习 Layer2 - zero-Merkle 树构建
- carterfeldman
- 发布于 2023-06-17 12:46
- 阅读 1580
本教程详细介绍了如何从零开始构建一个高效的零知识Merkle树(ZMT)实现,并讨论了如何构建仅需要O(log(n))存储的仅追加Merkle树。文章还探讨了如何生成和验证批量更新的Spiderman证明,并提供了TypeScript的实现代码。
这是 《黑客指南:从零构建zkVM的Layer 2》第2期的周播。
在本教程中,我们将:
- 学习如何构建一个高效的 zero merkle tree 实现,能够处理 万亿级叶子的树 的变更,并从零开始用 TypeScript 实现它。
- 学习如何构建一个 仅追加的merkle树,只需 O(log(n)) 的存储,并从零开始用 TypeScript 实现它。
- 学习 Spiderman proofs,以及如何高效生成/验证用一个 单一、简洁的证明 对 merkle树进行的 批量更新。
注意
在阅读本教程之前,强烈建议 首先完成 第一期,在这一期中我们涵盖了 merkle 树的基础知识,并将经常引用我们在上一期中所学的内容。
我无法创造的,我无法理解。
理查德·费曼
引言
在《黑客指南:Layer 2》第一期中,我们介绍了 merkle 树的基础知识,并构建了一个简单的 merkle 树数据库实现。
虽然我们构建的实现简单且适用于小型树,但我们之前的 merkle 树实现对处理大型树时会非常慢:
- 每当我们调用 getRoot(计算树的 merkle 根)时,都不得不重新哈希整个 merkle 树(O(2^height) 时间复杂度)
- 创建一个新的 merkle 树实例要求我们在构造函数中传入树的高度和大小为 2^height 的 一个叶子数组(内存同样是 O(2^n))
不幸的是,我们的 zkVM 需要与 大型(高度 > 32)和 稀疏(大多数叶子为零)的 merkle 树一起使用。
我们将在未来的章节中解释为什么会这样,但这与我们的 zkVM 将使用 merkle 树来可验证地存储和组织持久数据(将 merkle 树视为空间可验证的硬盘 + 文件系统)直观相关。
但是,我们并没有失去好运,因为我们可以利用 merkle 树的 自相似性 为我们的用例构建一个更高效的数据库。
Zero Hashes
为了开始解决构建更适合我们大型/稀疏用例的 merkle 树的问题,我们可以通过首先检查一个空的 merkle 树,并寻找我们可以利用的模式来获得一些洞见:
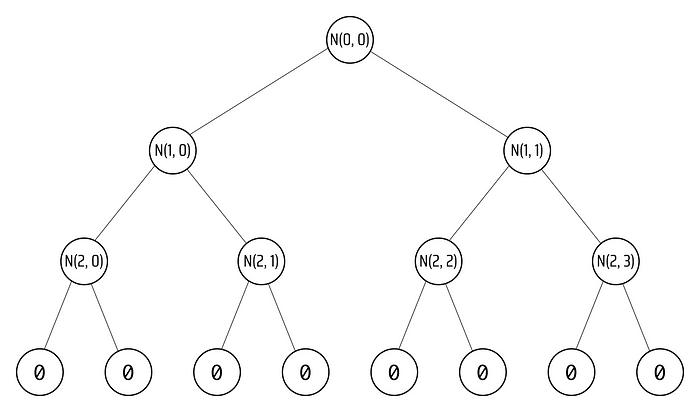
一个空的 merkle 树 (树高 = 3)
如果我们回忆起一个节点的值等于其子节点的哈希值,我们可以在具有相同值的节点周围绘制矩形:

由于底层级别的节点都有相同的值,因此上面的节点也将具有相同的值,因为上面节点的值仅依赖于下面节点的哈希
啊哈!当一个 merkle 树为空时,每个级别上的所有节点都有相同的值。空 merkle 树每个级别节点的值被称为 Zero Hashes,通常表示为 Zₙ,其中 n = TreeHeight - Level。
由于我们知道底层节点的值 Z ₀ = 0,让我们写一个关于 Zₙ. 的表达式。
回忆一下我们在上一期学到的计算 merkle 树中节点值的公式:
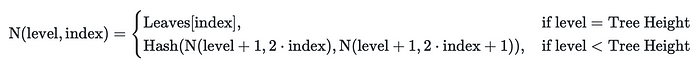
计算 merkle 树节点值的公式
我们只需为叶子插入 零,并利用我们在树中观察到的 按级别 的 自相似性 来写出 Zₙ 的表达式:
因此我们可以说,对于一个高度为 TreeHeight 的空 merkle 树:
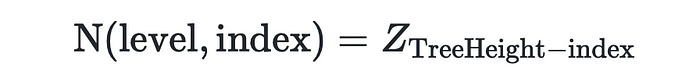
很好,现在让我们通过编写一个 TypeScript 函数来计算给定 treeHeight 的零哈希数组,以展示我们对零哈希的理解:
import shajs from "sha.js";
type MerkleNodeValue = string;
function hash(leftNode: MerkleNodeValue, rightNode: MerkleNodeValue) {
return shajs("sha256")
.update(leftNode + rightNode, "hex")
.digest("hex");
}
function computeZeroHashes(height: number): MerkleNodeValue[] {
let currentZeroHash = "0000000000000000000000000000000000000000000000000000000000000000";
const zeroHashes: MerkleNodeValue[] = [currentZeroHash];
for (let i = 1; i <= height; i++) {
currentZeroHash = hash(currentZeroHash, currentZeroHash);
zeroHashes.push(currentZeroHash)
}
return zeroHashes;
}
function example1(){
console.log("[example1] the first 32 zero hashes are: "+JSON.stringify(computeZeroHashes(32), undefined, 2));
}
example1();很好!现在我们已经写了一个计算零哈希的函数,我们可以编写一个获取空 merkle 树中任何节点值的函数,使用我们的零哈希:
function getNodeValue(treeHeight: number, level: number): MerkleNodeValue {
const zeroHashes = computeZeroHashes(treeHeight);
return zeroHashes[treeHeight - level];
}实现一个 ZMT 数据库
我们现在知道如何计算空 merkle 树中任何节点的值,让我们利用我们的知识编写一个高效的 merkle 树数据库。
在我们系列的前一篇中,我们已经证明,当你更新 merkle 树中的一个叶子时,只有沿叶子的 merkle 路径上的节点会变:

利用这个原理,我们构建一个只存储树中非零哈希节点的 merkle 树数据库,并遵循以下程序:
要找到节点 N(level, index) 的值:
- 检查它是否存在于数据库中。如果存在,返回值。
- 如果不存在,返回节点级别的对应零哈希
- 如果要更新一个节点,首先设置叶子,计算叶子的 merkle 路径,然后将所有新的节点值保存到数据库的 merkle 路径中
通过这种方式,我们将创建一个只需要存储非零哈希节点的数据库,完美适用于我们的大型稀疏 merkle 树!
让我们开始编写一个简单的数据存储,以遵循我们的从数据存储中获取节点的规则(如果存在则返回,否则回退到零哈希):
class NodeStore {
nodes: { [id: string]: MerkleNodeValue };
height: number;
zeroHashes: MerkleNodeValue[];
constructor(height: number) {
this.nodes = {};
this.height = height;
this.zeroHashes = computeZeroHashes(height);
}
contains(level: number, index: number): boolean {
// 检查节点是否存在于数据存储中
return Object.hasOwnProperty.call(this.nodes, level + "_" + index);
}
set(level: number, index: number, value: MerkleNodeValue) {
// 设置数据存储中的节点值
this.nodes[level + "_" + index] = value;
}
get(level: number, index: number): MerkleNodeValue {
if (this.contains(level, index)) {
// 如果节点在数据存储中,返回它
return this.nodes[level + "_" + index];
} else {
// 如果节点不在数据存储中,返回该节点级别的正确零哈希
return this.zeroHashes[this.height - level];
}
}
}很好!现在我们可以编写一个 ZeroMerkleTree 类,它使用 NodeStore:
class ZeroMerkleTree {
height: number;
nodeStore: NodeStore;
constructor(height: number) {
this.height = height;
this.nodeStore = new NodeStore(height);
}
}根据我们在上一期学到的内容,我们知道可以通过每次将索引除以 2 来计算节点的 merkle 路径:
function getMerklePathOfNode(level, index) {
const merklePath = [];
for (let currentLevel = level; currentLevel >= 0; currentLevel--) {
merklePath.push({
level: currentLevel,
index: index,
});
index = Math.floor(index / 2);
}
return merklePath;
}应用这项知识,让我们编写一个 setLeaf 函数,该函数根据与我们的 getMerklePathOfNode 函数和兄弟节点的奇偶哈希规则相同的逻辑在树中设置叶子并更新其 merkle 路径:
class ZeroMerkleTree {
height: number;
nodeStore: NodeStore;
constructor(height: number) {
this.height = height;
this.nodeStore = new NodeStore(height);
}
setLeaf(index: number, value: MerkleNodeValue) {
// 从叶子节点开始遍历叶子的 merkle 路径
let currentIndex = index;
let currentValue = value;
// 在循环中不要设置根节点(level = 0),因为它没有兄弟节点
for (let level = this.height; level > 0; level--) {
// 在树中设置当前节点
this.nodeStore.set(level, currentIndex, currentValue);
if (currentIndex % 2 === 0) {
// 如果当前索引是偶数,则它在右侧有一个兄弟节点(同一层,索引 = currentIndex + 1)
const rightSibling = this.nodeStore.get(level, currentIndex + 1);
currentValue = hash(currentValue, rightSibling);
} else {
// 如果当前索引是奇数,则它在左侧有一个兄弟节点(同一层,索引 = currentIndex - 1)
const leftSibling = this.nodeStore.get(level, currentIndex - 1);
currentValue = hash(leftSibling, currentValue);
}
// 将当前索引设置为父节点的索引
currentIndex = Math.floor(currentIndex / 2);
}
// 将根节点(level = 0,索引 = 0)设置为当前值
this.nodeStore.set(0, 0, currentValue);
}
}很好!让我们通过添加一个 getRoot 函数来检查它的工作情况,该函数返回 merkle 根。
class ZeroMerkleTree {
...
getRoot(): MerkleNodeValue {
return this.nodeStore.get(0, 0);
}
...
}把所有东西放在一起,我们得到了:
运行此函数得出的结果:[example2] the root is: 7e286a6721a66675ea033a4dcdec5abbdc7d3c81580e2d6ded7433ed113b7737 我们可以通过将其与我们在 前一期 中计算的相同叶子的树的 merkle 根进行比较来验证我们是否一切正常:
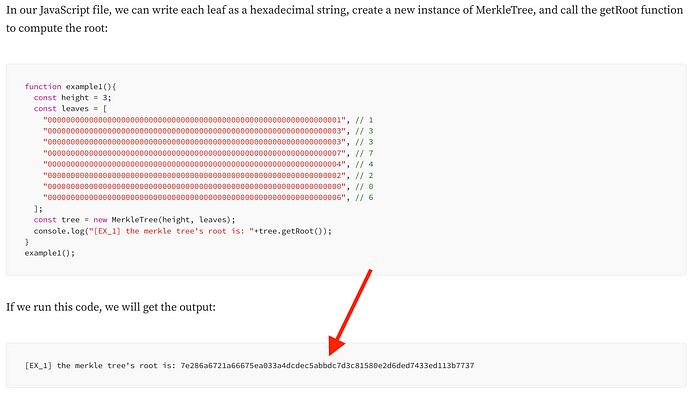
根匹配!
完美的匹配 🎉,现在我们可以通过在调用 setLeaf 时返回 delta merkle proof 来使其更有用。
回顾我们之前对 delta merkle proofs 的定义,我们将需要以下数据:
- 叶子的索引 (index)
- 叶子的 merkle 路径的兄弟节点 (siblings)
- 更改叶子之前的根 (oldRoot)
- 更改叶子之前的值 (oldValue)
- 更改叶子后根 (newRoot)
- 叶子的新值 (newValue)
type MerkleNodeValue = string; interface IDeltaMerkleProof { index: number; siblings: MerkleNodeValue[]; oldRoot: MerkleNodeValue; oldValue: MerkleNodeValue; newRoot: MerkleNodeValue; newValue: MerkleNodeValue; }
为此,我们可以修改 setLeaf 函数的开始部分,以在进行更新之前记录 oldRoot 和 oldValue 的值,并添加一个 siblings 数组来跟踪叶子的 merkle 路径的兄弟节点:
...
setLeaf(index: number, value: MerkleNodeValue): IDeltaMerkleProof {
// 获取旧根和旧值以进行 delta merkle proof
const oldRoot = this.nodeStore.get(0, 0);
const oldValue = this.nodeStore.get(this.height, index);
// 为 delta merkle proof 创建兄弟节点数组
const siblings: MerkleNodeValue[] = [];
...然后,我们可以修改循环体,在我们使用兄弟节点对 merkle 路径的节点进行哈希时,将兄弟节点的值也推入我们的 siblings 数组中:
...
setLeaf(index: number, value: MerkleNodeValue): IDeltaMerkleProof {
...
for (let level = this.height; level > 0; level--) {
// 在树中设置当前节点
this.nodeStore.set(level, currentIndex, currentValue);
if (currentIndex % 2 === 0) {
// 如果当前索引是偶数,则它在右侧有一个兄弟节点(同一层,索引 = currentIndex + 1)
const rightSibling = this.nodeStore.get(level, currentIndex + 1);
currentValue = hash(currentValue, rightSibling);
// 将右兄弟节点添加到 siblings 数组中
siblings.push(rightSibling); // <---- HERE
} else {
// 如果当前索引是奇数,则它在左侧有一个兄弟节点(同一层,索引 = currentIndex - 1)
const leftSibling = this.nodeStore.get(level, currentIndex - 1);
currentValue = hash(leftSibling, currentValue);
// 将左兄弟节点添加到 siblings 数组中
siblings.push(leftSibling); // <---- HERE
}
// 将当前索引设置为父节点的索引
currentIndex = Math.floor(currentIndex / 2);
}
...然后在函数结尾处,我们只需要使用我们的新变量返回一个 delta merkle proof:
setLeaf(index: number, value: MerkleNodeValue): IDeltaMerkleProof {
// 获取旧根和旧值以进行 delta merkle proof
const oldRoot = this.nodeStore.get(0, 0);
const oldValue = this.nodeStore.get(this.height, index);
// 为 delta merkle proof 创建兄弟节点数组
const siblings: MerkleNodeValue[] = [];
// 从叶子节点开始遍历叶子的 merkle 路径
let currentIndex = index;
let currentValue = value;
// 在循环中不要设置根节点(level = 0),因为它没有兄弟节点
for (let level = this.height; level > 0; level--) {
// 在树中设置当前节点
this.nodeStore.set(level, currentIndex, currentValue);
if (currentIndex % 2 === 0) {
// 如果当前索引是偶数,则它在右侧有一个兄弟节点(同一层,索引 = currentIndex + 1)
const rightSibling = this.nodeStore.get(level, currentIndex + 1);
currentValue = hash(currentValue, rightSibling);
// 将右兄弟节点添加到 siblings 数组中
siblings.push(rightSibling);
} else {
// 如果当前索引是奇数,则它在左侧有一个兄弟节点(同一层,索引 = currentIndex - 1)
const leftSibling = this.nodeStore.get(level, currentIndex - 1);
currentValue = hash(leftSibling, currentValue);
// 将左兄弟节点添加到 siblings 数组中
siblings.push(leftSibling);
}
// 将当前索引设置为父节点的索引
currentIndex = Math.floor(currentIndex / 2);
}
// 将根节点(level = 0,索引 = 0)设置为当前值
this.nodeStore.set(0, 0, currentValue);
return { // <--- HERE
index,
siblings,
oldRoot,
oldValue,
newValue: value,
newRoot: currentValue,
};
}把所有东西放在一起,我们可以复制我们在 前一期 中编写的 verifyDeltaMerkleProof 来检查 delta merkle proofs 是否有效, 代码:
让我们运行 JavaScript 看看效果如何:[example3]
delta merkle proof for index 0 is valid
[example3] delta merkle proof for index 1 is valid
[example3] delta merkle proof for index 2 is valid
[example3] delta merkle proof for index 3 is valid
[example3] delta merkle proof for index 4 is valid
[example3] delta merkle proof for index 5 is valid
[example3] delta merkle proof for index 6 is valid
[example3] delta merkle proof for index 7 is valid
[example3] the delta merkle proofs are:
[\
{\
"index": 0,\
"siblings": [\
"0000000000000000000000000000000000000000000000000000000000000000",\
"f5a5fd42d16a20302798ef6ed309979b43003d2320d9f0e8ea9831a92759fb4b",\
"db56114e00fdd4c1f85c892bf35ac9a89289aaecb1ebd0a96cde606a748b5d71"\
],\
"oldRoot": "c78009fdf07fc56a11f122370658a353aaa542ed63e44c4bc15ff4cd105ab33c",\
"oldValue": "0000000000000000000000000000000000000000000000000000000000000000",\
"newValue": "0000000000000000000000000000000000000000000000000000000000000001",\
"newRoot": "f06e424318b067ae608de0ef0035e9f48a2658cc59e7f94f9f94600b2a36eac6"\
},\
... /* 省略以简洁,查看代码网获取完整结果 */\
]成功了!所有的 delta merkle proofs 都是有效的!
链 Delta Merkle Proofs
除了验证 delta merkle proofs,另一个我们 zkVM 必须执行的重要检查被称为 链 delta merkle proof 验证。
链 delta merkle proof 验证确保一系列 delta merkle proofs 是顺序的,这意味着你已提供第一条 delta merkle proof 的 oldRoot 到该系列的最后一条 delta merkle proof 的 newRoot 的 所有 证明。
我们可以通过断言,每个系列中的 delta merkle proof 的 oldRoot 等于前一条 proof 的 newRoot 来执行此验证:
...
for(let i=0;i<deltaMerkleProofs.length;i++){
const deltaProof = deltaMerkleProofs[i];
if(!verifyDeltaMerkleProof(deltaProof)){ // 首先验证证明
console.error("[example4] ERROR: delta merkle proof for index "+deltaProof.index+" is INVALID");
throw new Error("invalid delta merkle proof");
}else if(i>0 && deltaProof.oldRoot !== deltaMerkleProofs[i-1].newRoot){ // <------ [HERE]
// 之前证明的新根应与此证明的旧根相同
console.error(
"[example4] ERROR: delta merkle proof for index "+deltaProof.index +
" has a different old root than the previous delta merkle proof's new root"
);
throw new Error("delta merkle proof root sequence mismatch");
}else{
console.log("[example4] delta merkle proof for index "+deltaProof.index+" is valid");
}
}
...让我们更新我们的代码以包括链 delta merkle proof 验证,并检查我们的代码是否正常工作, 代码:
运行示例4,我们得到结果:
[example4] delta merkle proof for index 0 is valid
[example4] delta merkle proof for index 1 is valid
[example4] delta merkle proof for index 2 is valid
[example4] delta merkle proof for index 3 is valid
[example4] delta merkle proof for index 4 is valid
[example4] delta merkle proof for index 5 is valid
[example4] delta merkle proof for index 6 is valid
[example4] delta merkle proof for index 7 is valid
[example4] the delta merkle proofs are:
[\
... /* 省略以简洁,查看代码网获取完整结果 */\
]太好了!没有错误 🎉,我们证明了我们所做的更改是有效的(delta merkle proof)且是顺序的(链 delta merkle proof)。
完成我们的 ZMT 数据库
我们想要实现的最后一个导入函数是 getLeaf,该函数返回叶子的值以及相应的 merkle 包含证明。要做到这一点,我们只需获取叶子的值,然后按照我们在 setLeaf 中用于获取对兄弟节点和根的 merkle proof 的相同策略遍历其 merkle 路径:
class ZeroMerkleTree {
...
getLeaf(index: number): IMerkleProof {
// 生成 merkle proof 的兄弟节点数组
const siblings: MerkleNodeValue[] = [];
// 获取用于 merkle proof 的叶子的值
const value = this.nodeStore.get(this.height, index);
// 从叶子节点开始遍历叶子的 merkle 路径
let currentIndex = index;
let currentValue = value;
// 在循环中不要设置根节点(level = 0),因为它没有兄弟节点
for (let level = this.height; level > 0; level--) {
if (currentIndex % 2 === 0) {
// 如果当前索引是偶数,则它在右侧有一个兄弟节点(同一层,索引 = currentIndex + 1)
const rightSibling = this.nodeStore.get(level, currentIndex + 1);
currentValue = hash(currentValue, rightSibling);
// 将右兄弟节点添加到 siblings 数组中
siblings.push(rightSibling);
} else {
// 如果当前索引是奇数,则它在左侧有一个兄弟节点(同一层,索引 = currentIndex - 1)
const leftSibling = this.nodeStore.get(level, currentIndex - 1);
currentValue = hash(leftSibling, currentValue);
// 将左兄弟节点添加到 siblings 数组中
siblings.push(leftSibling);
}
// 将当前索引设置为父节点的索引
currentIndex = Math.floor(currentIndex / 2);
}
// 当前值为根节点
const root = currentValue;
return {
root,
siblings,
index,
value,
};
}
...我们现在可以将所有内容放在一起并使用我们在 前一篇中 编写的 verifyMerkleProof 函数来验证通过 getLeaf 生成的 merkle proof ( 完整代码 gist):参见这里
...
function example5() {
const leavesToSet = [\
"0000000000000000000000000000000000000000000000000000000000000001", // 1\
"0000000000000000000000000000000000000000000000000000000000000003", // 3\
"0000000000000000000000000000000000000000000000000000000000000003", // 3\
"0000000000000000000000000000000000000000000000000000000000000007", // 7\
"0000000000000000000000000000000000000000000000000000000000000004", // 4\
"0000000000000000000000000000000000000000000000000000000000000002", // 2\
"0000000000000000000000000000000000000000000000000000000000000000", // 0\
"0000000000000000000000000000000000000000000000000000000000000006", // 6\
];
const tree = new ZeroMerkleTree(3);
const deltaMerkleProofs = leavesToSet.map((leaf, index) => tree.setLeaf(index, leaf));
// 验证 delta merkle proofs
for (let i = 0; i < deltaMerkleProofs.length; i++) {
const deltaProof = deltaMerkleProofs[i];
if (!verifyDeltaMerkleProof(deltaProof)) {
console.error("[example5] ERROR: delta merkle proof for index " + deltaProof.index + " is INVALID");
throw new Error("invalid delta merkle proof");
} else if (i > 0 && deltaProof.oldRoot !== deltaMerkleProofs[i - 1].newRoot) {
// 之前证明的新根应与此证明的旧根相同
console.error(
"[example5] ERROR: delta merkle proof for index " + deltaProof.index +
" has a different old root than the previous delta merkle proof's new root"
);
throw new Error("delta merkle proof root sequence mismatch");
} else {
console.log("[example5] delta merkle proof for index " + deltaProof.index + " is valid");
}
}
// 为了避免杂乱无章,不打印 delta merkle proofs
// console.log("[example5] the delta merkle proofs are:\n" + JSON.stringify(deltaMerkleProofs, null, 2));
// 验证每个叶子的 merkle proof
for (let i = 0; i < leavesToSet.length; i++) {
const proof = tree.getLeaf(i);
if (!verifyMerkleProof(proof)) {
console.error("[example5] ERROR: merkle proof for index " + proof.index + " is INVALID");
throw new Error("invalid merkle proof");
} else if (proof.value !== leavesToSet[i]) {
console.error("[example5] ERROR: merkle proof for index " + proof.index + " has the wrong value");
throw new Error("merkle proof value mismatch");
} else {
console.log("[example5] merkle proof for index " + proof.index + " is valid");
}
console.log("merkle proof for index " + proof.index + ": " + JSON.stringify(proof, null, 2));
}
}
example5();运行代码我们得到的结果:
[example5] delta merkle proof for index 0 is valid
[example5] delta merkle proof for index 1 is valid
[example5] delta merkle proof for index 2 is valid
[example5] delta merkle proof for index 3 is valid
[example5] delta merkle proof for index 4 is valid
[example5] delta merkle proof for index 5 is valid
[example5] delta merkle proof for index 6 is valid
[example5] delta merkle proof for index 7 is valid
[example5] merkle proof for index 0 is valid
merkle proof for index 0: {
"root": "7e286a6721a66675ea033a4dcdec5abbdc7d3c81580e2d6ded7433ed113b7737",
"siblings": [\
"0000000000000000000000000000000000000000000000000000000000000003",\
"6b0e4bcd4368ba74e6a99ee69334c2593bcae1170d77048854d228664218c56b",\
"81b1e323f0e91a785dfd155817e09949a7d66fe8fdc4f31f39530845e88ab63c"\
],
"index": 0,
"value": "0000000000000000000000000000000000000000000000000000000000000001"
}
[example5] merkle proof for index 1 is valid
... /* 省略以简洁,查看代码网获取完整结果 */精彩!
我们现在已经编写了一个可以与我们的 zkVM 一起使用的 merkle 树数据库 🎉🎉🎉
为了展示我们新的超级强大的 merkle 树,让我们创建一个高度为 50 的 merkle 树,具有 1,125,899,906,842,624 的叶子,并为第 1337 和第 999,999,999,999 个节点设置值(链接代码)
在每个叶子 64 字节的存储下,我们之前的实现将需要 64PB 的 RAM 仅用于存储树(甚至现代超级计算机都无法做到这一点),而我们新的 ZeroMerkleTree 实现可以在瞬间在笔记本电脑上完成,只消耗 6400 字节:// 完整代码请查看这里
...
function example6() {
const tree = new ZeroMerkleTree(50);
const deltaA = tree.setLeaf(999999999999, "0000000000000000000000000000000000000000000000000000000000000008");
const deltaB = tree.setLeaf(1337, "0000000000000000000000000000000000000000000000000000000000000007");
const proofA = tree.getLeaf(999999999999);
const proofB = tree.getLeaf(1337);
console.log("verifyDeltaMerkleProof(deltaA): " + verifyDeltaMerkleProof(deltaA));
console.log("verifyDeltaMerkleProof(deltaB): " + verifyDeltaMerkleProof(deltaB));
console.log("deltaA.newRoot === deltaB.oldRoot: " + (deltaA.newRoot === deltaB.oldRoot));
console.log("verifyMerkleProof(proofA): " + verifyMerkleProof(proofA));
console.log("verifyMerkleProof(proofB): " + verifyMerkleProof(proofB));
console.log("proofA: " + JSON.stringify(proofA, null, 2));
console.log("proofB: " + JSON.stringify(proofB, null, 2));
}
example6();
这段代码打印的结果:verifyDeltaMerkleProof(deltaA): true
verifyDeltaMerkleProof(deltaB): true
deltaA.newRoot === deltaB.oldRoot: true
verifyMerkleProof(proofA): true
verifyMerkleProof(proofB): true
proofA: {
"root": "40db8b6edad868d911c8b9aea2692ee80b2e87ac407b8d1a5efe30419e843991",
"siblings":
... /* 省略以简洁,查看代码实验室以获取完整结果 */
],
"index": 999999999999,
"value": "0000000000000000000000000000000000000000000000000000000000000008"
}
proofB: {
"root": "40db8b6edad868d911c8b9aea2692ee80b2e87ac407b8d1a5efe30419e843991",
"siblings": [\
... /* 省略以简洁,查看代码实验室以获取完整结果 */\
],
"index": 1337,
"value": "0000000000000000000000000000000000000000000000000000000000000007"
}我们已经攀登了不可能的高峰,建立了一个为我们的 zkVM 准备的 merkle 树,感谢 ZeroHashes 和我们的 ZMT 💪
仅追加 Merkle 树
我们的 ZMT 实现非常适合我们的 zkVM 使用案例,但是在构建传统区块链(EVM/zkEVM)时,存储可能会昂贵到使得即使是我们的 ZMT 在可验证事件日志等用例中也会证明过于昂贵。
我们将在未来的章节中详细讨论可验证事件日志,并探索无信任跨链桥梁,但就目前而言,了解这些仅写入的 merkle 树对于无信任地将数据和资产从第一层桥接到第二层至关重要。
可验证的事件日志
可验证事件日志的基本理论是我们希望允许智能合约在 merkle 树的叶子中记录事件。每当发生新事件时,我们就将一个叶子追加到 merkle 树(将 merkle 树中的下一个非零叶设置为该事件的哈希)并计算更新的根。然后,你可以使用零知识证明或第二层对这些事件进行链外处理,并提交证明,证明你已经将所有事件同步到最新的事件日志根,从而提供无信任的数据从第一层到第二层的传输。
使用案例中最重要的属性是智能合约只需要将叶子写入 merkle 树,而不必重新读取之前的事件叶子(我们只关心读取最新的根)。
通过对 零散 Hashes 的理解以及一些巧妙的策略,我们发现 我们只需要在链上存储 O(log(N)) 哈希即可构建一个高度为 N 的仅追加 merkle 树!
和之前一样,让我们通过可视化在追加叶子时 merkle 树的变化,看看是否能找到任何模式。
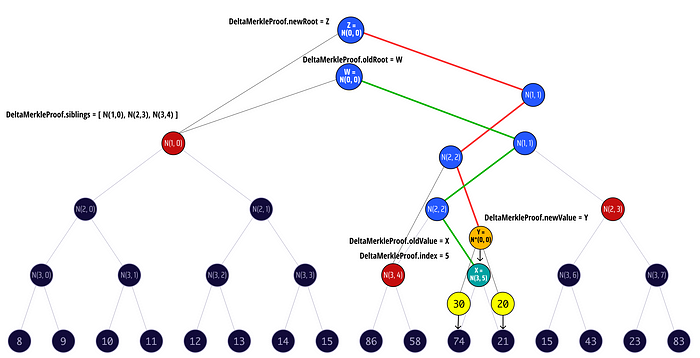
在下面的动画中,我们可视化了从添加一个叶子而来的 delta merkle 证明结果,具体如下:
- 紫色 节点代表正被追加的 叶子
- 蓝色 节点代表叶子 merkle 路径
- 红色 节点代表 兄弟节点
请记住,我们的目标是能够以某种方式计算新 merkle 根,同时存储尽可能少的数据。我们还知道从之前的章节中计算 merkle 树根所需的信息称为 merkle 证明,并包含以下信息:
- 索引(叶子的索引)
- 值(叶子的值)
- 兄弟节点(叶子 merkle 路径的兄弟节点)
在我们的仅追加 merkle 树的情况下,索引和值将被传递给函数,因此,计算所需的唯一缺失信息是用于使用存储在我们合约中的数据计算下一个 merkle 证明的兄弟节点的方式。如果我们使用前一节的 ZMT 实现,我们将不得不将树中的所有节点存储在链上,这是不可取的。
我们可能会以某种方式通过存储前一个节点的 merkle 证明,并以某种方式编写一个函数,从前一个节点的 merkle 证明中计算出新的兄弟节点来解决这个问题。
如果我们能够做到这一点,我们可以通过以下每次将叶子追加到树中的过程,达到 O(log(n)) 存储的目标:
- 从智能合约存储中读取之前的 merkle 证明,并将索引递增 1
- 以某种方式使用零散 Hashes 和之前的 merkle 证明计算正在追加的叶子的新的兄弟节点
- 使用新的兄弟节点和我们正在追加的值计算新的 merkle 根,然后将旧 merkle 证明用新追加的叶子的 merkle 证明覆盖到智能合约存储中
这当然引发了一个问题:是否可以仅使用零散 Hashes 和之前的 merkle 证明来计算我们仅追加 merkle 树中下一个叶子的兄弟节点?
让我们再次检查动画,但这一次让我们关注每当追加叶子到树时兄弟节点是如何变化的。我们将所有兄弟节点着色为红色,但这次如果它不是之前节点的 merkle 证明的兄弟节点,我们将兄弟的文本变成黄色:
开始看到模式了吗?破解这个难题的关键是要记住兄弟节点只是叶子的 merkle 路径上的相邻节点,因此当从叶子 N 过渡到叶子 N+1 时:
- 在叶子 N 和叶子 N+1 的 merkle 路径相同的层上,你可以在叶子 N+1 的 merkle 证明中重用叶子 N 的 merkle 证明中的兄弟节点
- 在叶子 N 和叶子 N+1 的 merkle 路径不同的层上,你需要以某种方式计算出新的兄弟节点。
太好了!因此在 merkle 路径没有变化的层上,我们知道可以直接重用前一个叶子的证明的兄弟节点,但对第二种情况呢?
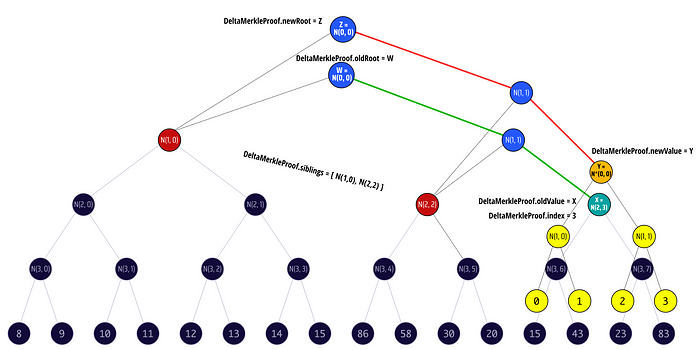
让我们检查更多的追加过渡,以获取一些直觉:
请注意,由于它是一个仅追加的 merkle 树,因此我们的叶子索引始终在增加,从而我们的路径始终向右移动。
让我们写下关于树中 Leaf[n] 和 Leaf[n+1] 的 merkle 路径/兄弟节点之间关系的已知信息,然后试图从我们所知道的事实推导出一个公式:

抱歉插入图像,medium 不支持 LaTeX,因此我无法将其内联
哈哈!因此生成 Leaf[n+1] 的 merkle 证明所需的唯一信息是:
- 树的零散 Hashes
- Leaf[n] 的兄弟节点/值
- Leaf[n] 的 merkle 路径(我们可以通过兄弟节点和自值计算得出!)
- Leaf[n+1] 的值
这真很酷,看起来构建我们的仅追加 merkle 树时需要存储的内容就是最新叶子的 merkle 证明!
根据上述事实,让我们编写我们的实现:
class AppendOnlyMerkleTree {
height: number;
lastProof: IMerkleProof;
zeroHashes: MerkleNodeValue[];
constructor(height: number){
this.height = height;
this.zeroHashes = computeZeroHashes(height);
// 创建一个所有零散 Hash 的虚拟证明以进行初始化(在追加任何叶子之前,我们知道所有的兄弟节点将是零散 Hash,因为这是一个空树)
this.lastProof = {
root: this.zeroHashes[this.height],
siblings: this.zeroHashes.slice(0, this.height),
index: -1,
value: this.zeroHashes[this.height],
};
}
appendLeaf(leafValue: string): IDeltaMerkleProof {
const oldMerklePath = computeMerklePathFromProof(this.lastProof.siblings, this.lastProof.index, this.lastProof.value);
// 获取旧根和旧值以用于 delta merkle 证明
const oldRoot = this.lastProof.root;
// 旧值将始终为空,这就是它的仅追加树的怪癖 :P
const oldValue = "0000000000000000000000000000000000000000000000000000000000000000";
const prevIndex = this.lastProof.index;
// 仅追加树 = 新索引始终是旧索引 + 1
const newIndex = prevIndex + 1;
// 保留旧兄弟节点以便可以用于我们的 delta merkle 证明
const oldSiblings = this.lastProof.siblings;
const siblings: MerkleNodeValue[] = [];
let multiplier = 1;
for(let level = 0; level < this.height; level++){
// 获取当前级别上前一个叶子的 merkle 路径节点的索引
const prevLevelIndex = Math.floor(prevIndex/multiplier);
// 获取当前级别上新叶子的 merkle 路径节点的索引
const newLevelIndex = Math.floor(newIndex/multiplier);
if(newLevelIndex === prevLevelIndex){
// 如果该级别上的 merkle 路径节点索引没有变化,我们可以重用旧兄弟节点
siblings.push(oldSiblings[level]);
}else{
// 如果这个级别上的 merkle 路径节点索引发生了变化,我们需要检查新的 merkle 路径节点索引是左子节点还是右子节点
if(newLevelIndex % 2 === 0){
// 如果新的 merkle 路径节点索引是偶数,则新的 merkle 路径节点是左子节点,
// 因此 merkle 路径节点的兄弟节点是右子节点,
// 因此我们的兄弟节点的索引大于我们的 merkle 路径节点,
// 因此兄弟节点必须是一个零散 Hash
// QED
siblings.push(this.zeroHashes[level]);
}else{
// 如果新的 merkle 路径节点是奇数,则其兄弟节点的索引小于一个,因此其兄弟节点必须是当前级别的前一个 merkle 路径节点
siblings.push(oldMerklePath[level]);
}
}
multiplier = multiplier * 2;
}
const newRoot = computeMerkleRootFromProof(siblings, newIndex, leafValue);
this.lastProof = {
root: newRoot,
siblings: siblings,
index: newIndex,
value: leafValue,
};
return {
index: this.lastProof.index,
siblings,
oldRoot,
oldValue,
newRoot,
newValue: leafValue,
};
}
}看起来不错,让我们使用我们之前的 verify delta merkle proof 函数对其进行测试,以确保它正确工作.
当我们运行 example7 时,我们得到的输出是:
verifyDeltaMerkleProof(deltaA): true
verifyDeltaMerkleProof(deltaB): true
deltaA.newRoot === deltaB.oldRoot: true
deltaA: {
"index": 0,
"siblings": [\
... /* 省略以简洁,查看代码实验室以获取完整结果 */\
],
"oldRoot": "e833d7a67160e68bf4c9044a53077df2727ad00cf36f4949c7b681a912140cbb",
"oldValue": "0000000000000000000000000000000000000000000000000000000000000000",
"newRoot": "bfe0338f3c07c1ff64514ccde5d0e4535b88c9093454b29de1590414c721abb1",
"newValue": "0000000000000000000000000000000000000000000000000000000000000008"
}
deltaB: {
"index": 1,
"siblings": [\
... /* 省略以简洁,查看代码实验室以获取完整结果 */\
],
"oldRoot": "bfe0338f3c07c1ff64514ccde5d0e4535b88c9093454b29de1590414c721abb1",
"oldValue": "0000000000000000000000000000000000000000000000000000000000000000",
"newRoot": "3b6c4c5cf467972101c5236a32eb2f5e23c66fab942352d1e7003660f83f66b2",
"newValue": "0000000000000000000000000000000000000000000000000000000000000007"
}
verifyDeltaMerkleProof(delta[0]): true
verifyDeltaMerkleProof(delta[1]): true
verifyDeltaMerkleProof(delta[2]): true
verifyDeltaMerkleProof(delta[3]): true
verifyDeltaMerkleProof(delta[4]): true
verifyDeltaMerkleProof(delta[5]): true
verifyDeltaMerkleProof(delta[6]): true
verifyDeltaMerkleProof(delta[7]): true
verifyDeltaMerkleProof(delta[8]): true
verifyDeltaMerkleProof(delta[9]): true
verifyDeltaMerkleProof(delta[10]): true
verifyDeltaMerkleProof(delta[11]): true
verifyDeltaMerkleProof(delta[12]): true
verifyDeltaMerkleProof(delta[13]): true
verifyDeltaMerkleProof(delta[14]): true
verifyDeltaMerkleProof(delta[15]): true
verifyDeltaMerkleProof(delta[16]): true
verifyDeltaMerkleProof(delta[17]): true
verifyDeltaMerkleProof(delta[18]): true
verifyDeltaMerkleProof(delta[19]): true
verifyDeltaMerkleProof(delta[20]): true
verifyDeltaMerkleProof(delta[21]): true
verifyDeltaMerkleProof(delta[22]): true
verifyDeltaMerkleProof(delta[23]): true
verifyDeltaMerkleProof(delta[24]): true
verifyDeltaMerkleProof(delta[25]): true
verifyDeltaMerkleProof(delta[26]): true
verifyDeltaMerkleProof(delta[27]): true
verifyDeltaMerkleProof(delta[28]): true
verifyDeltaMerkleProof(delta[29]): true
verifyDeltaMerkleProof(delta[30]): true
verifyDeltaMerkleProof(delta[31]): true
verifyDeltaMerkleProof(delta[32]): true
verifyDeltaMerkleProof(delta[33]): true
verifyDeltaMerkleProof(delta[34]): true
verifyDeltaMerkleProof(delta[35]): true
verifyDeltaMerkleProof(delta[36]): true
verifyDeltaMerkleProof(delta[37]): true
verifyDeltaMerkleProof(delta[38]): true
verifyDeltaMerkleProof(delta[39]): true
verifyDeltaMerkleProof(delta[40]): true
verifyDeltaMerkleProof(delta[41]): true
verifyDeltaMerkleProof(delta[42]): true
verifyDeltaMerkleProof(delta[43]): true
verifyDeltaMerkleProof(delta[44]): true
verifyDeltaMerkleProof(delta[45]): true
verifyDeltaMerkleProof(delta[46]): true
verifyDeltaMerkleProof(delta[47]): true
verifyDeltaMerkleProof(delta[48]): true
verifyDeltaMerkleProof(delta[49]): true成功!
因为我们只在类中存储一个 merkle 证明,所以我们的仅追加 merkle 树只需要 O(log(n)) 存储 🎉
蜘蛛侠证明
有时我们想要更新树的一整部分:
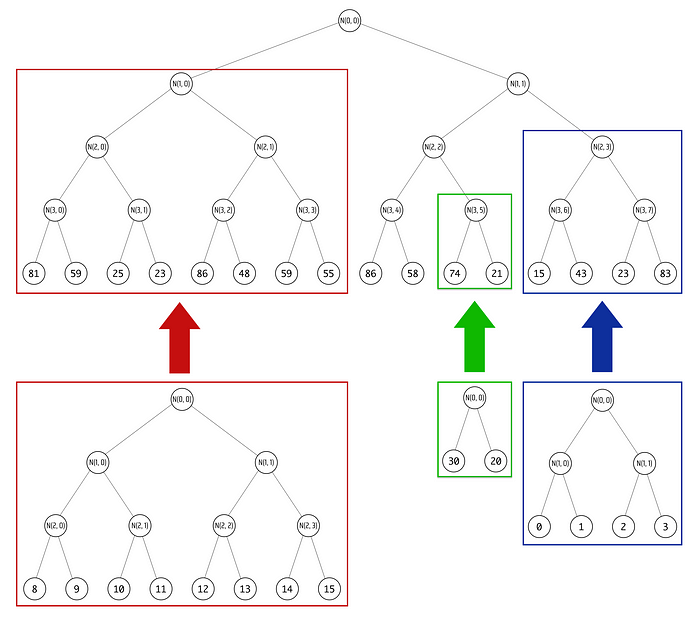
使用我们的 ZMT 实现,我们可以通过 逐个更新每个叶子 来做到这一点,但也许有更好的方法来更新一批叶子。
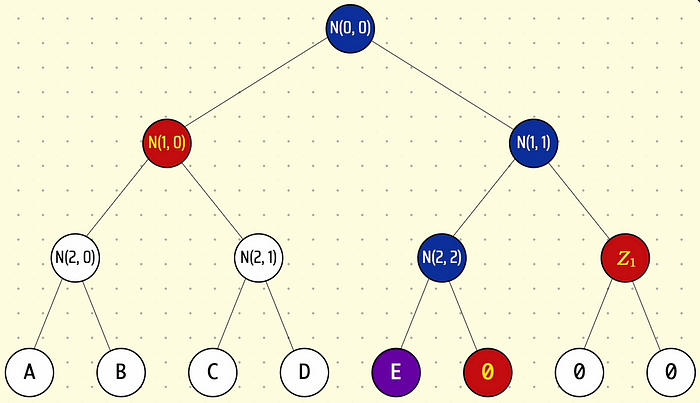
让我们先尝试左侧以红色高亮显示的树:

我们希望用底部树替换顶部子树
请注意,根节点为 N(1,0) 的子树在我们的大树中看起来与底部的更新小树相同,只是值不同。
如果我们再仔细看看顶部的大树,子树上方的节点组成了一个自己的小高度为 1 的树:
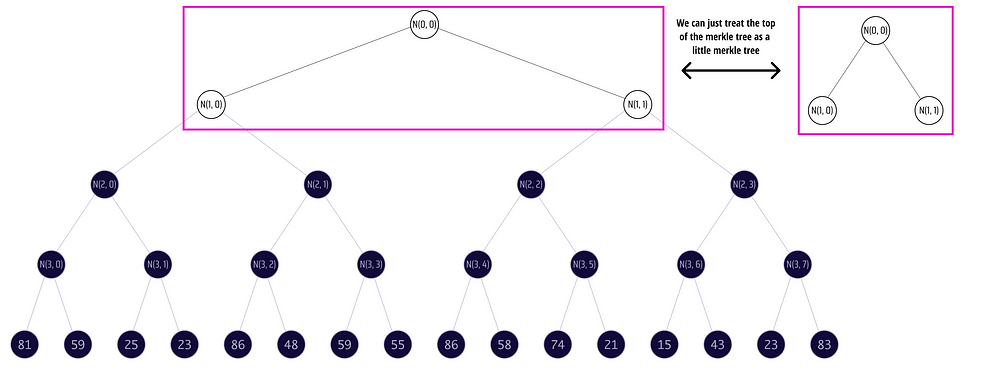
太好了!我们知道如何更新 merkle 树的叶子,让我们开始从我们所知道的信息中构建 delta merkle 证明。
- 我们知道我们要更新的节点是 N(1,0),因此 delta merkle 证明的索引将为 1。
- 我们知道 delta merkle 证明的兄弟节点将是 [N(1,1)],因为 N(1,0) 是 merkle 路径上唯一的节点,而它的兄弟是 N(1,1)
- 我们知道 delta merkle 证明的旧根将是我们的旧 N(0,0)
- 我们知道我们的旧值是 N(1,0) 的值,因为那是我们要更新的“叶子”
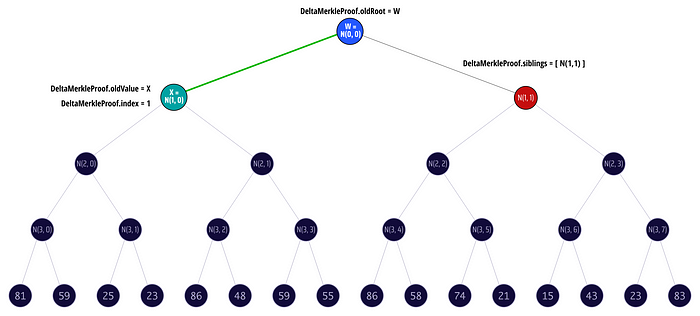
现在我们所要做的就是更新叶子,并应用我们在上一篇节目中学到的 delta merkle 证明的规则:
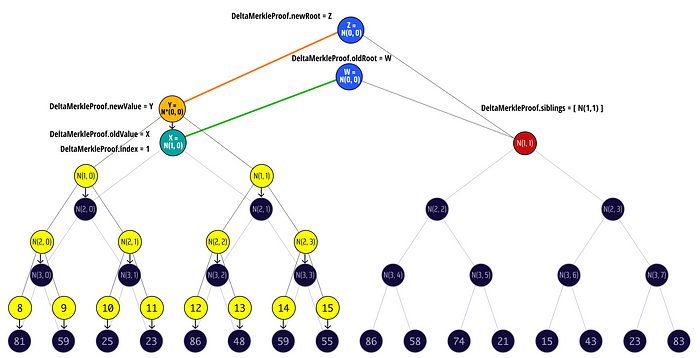
太棒了!现在我们知道了如何高效地替换 merkle 树的部分并生成 delta merkle 证明以证明我们的更改的有效性。
对于我们要替换的其余子树,我们只需根据相同的规则依次更新它们:
目前,我们不会在 TypeScript 中为此操作编写代码,因为我们只需要在接下来的章节中在我们的算术电路中编写这一逻辑的原因。
结论
如果你坚持到这里,干得不错,你现在知道了构建我们的 zkVM 所需的关于 merkle 树的所有信息!
在下一个章节中,我们将使用 plonky2 编写我们的第一个零知识电路,并开始实现我们的 zkVM!

感谢我们的赞助商 OAS 和 QED,你可以在 Twitter 上关注 OAS @OASNetwork
作者简介 — 在 Twitter 上关注 @cmpeq 或查看我的 简介页面。
- 原文链接: medium.com/@carterfeldma...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,在这里修改,还请包涵~
- 翻译
- 学分: 0
- 分类: 密码学
- 标签: Merkle树 ZMT 仅追加Merkle树 Spiderman证明 Typescript 零知识证明
- PKI (公钥基础设施)已变:量子时代与谷歌的默克尔树证书方案 93 浏览
- 民主事物的再思考:构建共识发现工具 116 浏览
- Zero 链: 技术定位报告 195 浏览
- 以太坊亟需的两大深度改造——二进制树 + VM 改造 224 浏览
- 以太坊 2029 Strawmap 傻瓜指南 262 浏览
- 不实的断言:攻破 6 个 zkVMs 188 浏览
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 348 浏览
- 零知识编年史:群 264 浏览
- 以太坊执行层优化:状态树与虚拟机 440 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 303 浏览
- 首次 ZK 攻击发生,且出乎意料 304 浏览
- Vitalik: 以太坊量子抵抗路线图 280 浏览


