高级密码学原语——群、有限域、椭圆曲线与配对

高级加密原语 — 群、有限域、椭圆曲线和配对。

在进行研究或工作于高级加密协议时，你可能会注意到许多基本元素被反复使用。这些元素被称为高级加密原语。在本文中，我们将探讨最重要的元素，例如群、有限域、椭圆曲线和配对。这些元素是密码学的基石，在设计和实现许多高级协议（例如数字签名方案、多方计算（MPC）和零知识证明（ZKP））中发挥着关键作用。依我看，拥有扎实的基础和对这些原语的深入理解在密码学工作中是非常有帮助的。让我们开始吧！

群

定义

群 G 是一组数字，配备有 单一 操作 — 仅限加法或乘法。如果操作是加法，则群称为 加法群。如果操作是乘法，则群称为 乘法群。为了简化，在本节中，我们将探讨加法群，记作 (G, +)。乘法群和加法群共享相同的属性，因此仅复习加法群就足够了。

有限群是指具有有限个元素的群。在密码学中，我们主要使用有限群；因此，本文章中的所有群如果未特别说明，均为有限群。

一般而言，有限群 (G_p, +) 由整数 p 构成，包含 p 个元素 {0, 1, 2, … , p-1} ，并配备了 模 p 加法 操作。

属性

有限群具有以下属性：

1. 闭合性

对于群中的任意两个元素 a, b，操作 (a+b) 的结果也是群中的一个元素。

2. 结合性

对于群中的任意三个元素 a, b, c，该等式成立：

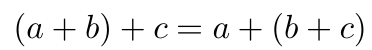
群的结合性。

3. 单位元素

群中存在单位元素 0，对于它：

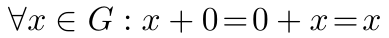
单位元素方程。

也就是说，将单位元素加到群中的任何元素上均不改变该元素。

4. 逆元素

对于群中的任意元素 x，存在一个逆元素 (-x)，满足：

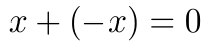
逆元素方程。

也就是说，元素与其逆元素的加法结果为单位元素。

5. 群的阶

有限群中元素的数量称为该群的阶，用 |G| 表示。

6. 生成元

我们注意到使用元素 1 及群操作 模 p 加法，可以生成群中的所有元素，满足：

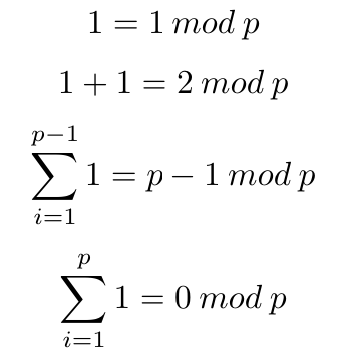
群的生成元。

生成群中所有元素的元素称为 生成元。

7. 子群

有限群可能由许多其他子群组成。每个子群本身也是一个有限群。例如，群 (G_6, + mod 6) 具有一个子群 ({0,2,4}, + mod 6)，该子群由生成元元素 2 生成，有 3 个元素 {0,2,4} ，满足：

2 = 2 mod 6

4 = 2+2 mod 6

0 = 2+2+2 mod 6

8. 元素的阶

给定群中的元素 X，使得 nX= 0 的最小整数 n 称为 X 的阶。

示例

让我们探讨一个有 6 个元素 {0,1,2,3,4,5} 的群 G_6，操作为 模 6 加法。这被记作 (G_6, +)。该群具有以下属性。

• 群的阶

群的阶为 6，即该群包含 6 个元素 {0,1,2,3,4,5}。

• 操作

该群的操作是 模 6 加法。在该群中对任意两个元素应用此操作，结果也是群中的一个元素。例如：

2 + 3 = 5 mod 6

1 + 4 = 0 mod 6

4 + 5 = 3 mod 6

• 单位元素

该群的单位元素为 0。

• 生成元

该群的生成元为 1，通过 模 6 加法 可生成群中的所有元素。

• 元素的阶

对于有限群 G_6，1 的阶为 6，而 2 的阶为 3，因为：

元素 1 和 2 的阶。

• 逆

群中的每个元素 x 都有一个逆元素 -x，使得 x + (-x) = 0。例如：

1 + 5 = 0 mod 6

2 + 4 = 0 mod 6

• 子群

群 (G_6, +) 有一个子群 ({0, 2, 4}, +)。该子群的阶为 3，单位元素为 2。

有限域

定义

一个域 F 是一组数字，配备有 两个 操作：加法和乘法。一个域的例子可能是整数域 Z、实数域 R、复数域 C。它记作 F_q。

有限域是一个拥有有限数量元素的域。在密码学中，我们主要使用有限域；因此，本文章中的所有域如果未特别说明，均为有限域。

一般而言，质数 p 的有限域 F_q 包含 q 个元素 {0, 1, 2, …, q-1}，其中 q=p^n。它配备有两种操作：模 p 加法 和 模 p 乘法。

属性

有限域具有以下属性。

1. 闭合性

在域中对任意两个元素进行加法或乘法操作的结果也是域中的一个元素。

2. 域的阶

域中元素的数量称为域的阶，用 q 表示。

3. 质数域

有限域的阶总是质数的幂，表示为：

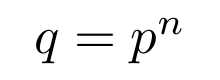
域的阶与质数关系

其中：

• p 是一个质数
• n 是一个正整数。

如果 n=1，则该有限域称为 质数域。

4. 单位元素

与群中单一单位元素的情况相对，一个有限域有 2 个单位元素。

第一个是 加法单位元素，这是一个元素，当它加到域中的任何元素上时，元素不变。

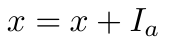
加法单位元素

其中：

• x：域中的任意元素。
• I_a：加法单位元素。

第二个是 乘法单位元素，这是一个元素，当它与域中的任何元素相乘时，元素不变。

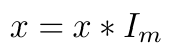
乘法单位元素

其中：

• x：域中的任意元素。
• I_m：乘法单位元素。

5. 逆元素

与单位元素类似，域中每个元素都有两个逆元素：加法逆元素 和 乘法逆元素。

加法逆元素 是当加到原元素上等于 0 的元素。

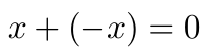
加法逆元素

其中：

• x：域中的任意元素。
• -x：x 的加法逆元素。

乘法逆元素 是当与原元素相乘等于 1 的元素。

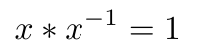
乘法逆元素

其中：

• x：域中的任意元素。
• x^-1：x 的乘法逆元素。

示例

让我们探讨一个特定的质数 p=5 的有限域 F_5，包含 5 个元素 {0, 1, 2, 3, 4}。

1. 域的阶

域的阶 q=5，即该域包含 5 个元素 {0, 1, 2, 3, 4}。

2. 质数域

质数 p=5，因此 q=p^n 在 n=1 时成立。这是一个质数域。

3. 域的操作

该域配备有 2 种操作：

• 模 5 加法
• 模 5 乘法

4. 单位元素

该域具有 2 个单位元素：

• 加法单位元素是 0，因为 x + 0 = x 对域中的所有元素均成立。
• 乘法单位元素是 1，因为 x * 1 = x 对域中的所有元素均成立。

5. 逆元素

对于域中的每个元素，存在两个逆元素：

• 加法逆元素。例如，3 是 2 的加法逆元素，因为：

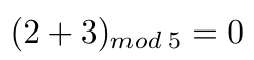
2 的加法逆元素

• 乘法逆元素。例如，4 是自身的乘法逆元素，因为：

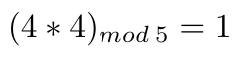
4 的乘法逆元素

椭圆曲线

定义

在数学中，椭圆曲线 E 是满足下列方程的点集 P(x, y)：

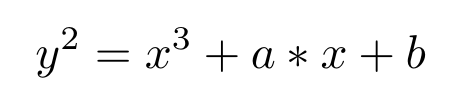
椭圆曲线方程。

其中

• x, y : 实数
• a, b : 整数

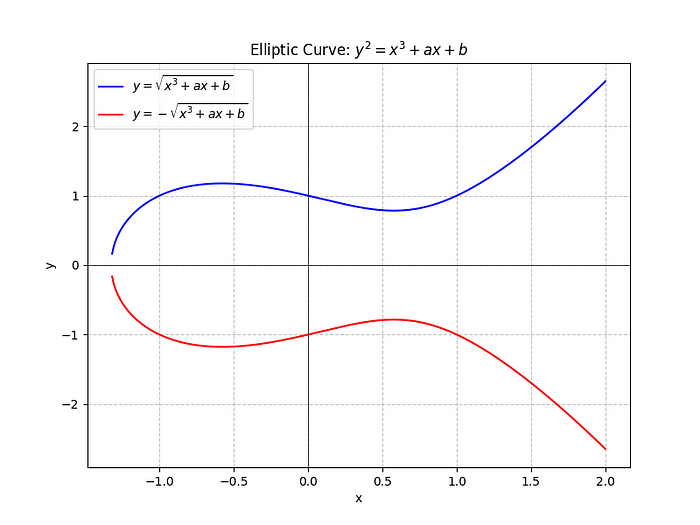
在实数 R 上，椭圆曲线如下图所示：

实数 R 上的椭圆曲线。

在加密技术中，我们通常利用 有限域上的椭圆曲线，这意味着 x, y 不是真实数字，而是有限域 F_q 的元素。它看起来像是一组随机散布的点，这与实数域上的曲线大相径庭。这是因为这些点是在配备了两种操作（模 p 加法 和 模 p 乘法）的有限域 F_q 上定义的。一种常用的椭圆曲线 BN128 在下图中展示：

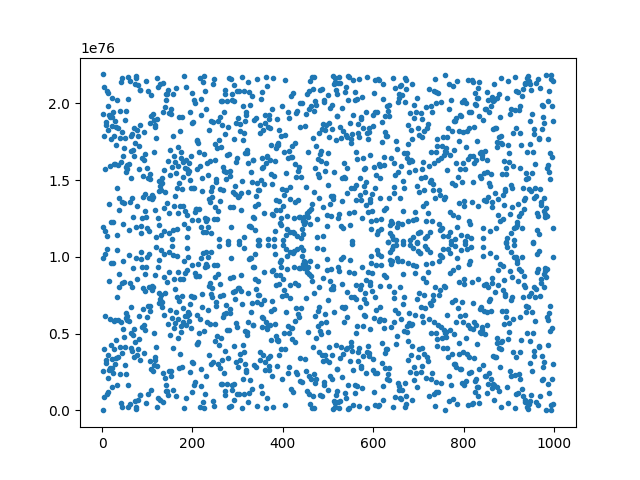
BN128 椭圆曲线图。

属性

椭圆曲线具有以下属性。

1. 生成点 (G)

有限域 F_q 上椭圆曲线 E 的生成点 G 是曲线上的一个点，可以用来生成曲线的大循环子群。这意味着曲线上的每个点都可以表示为 G 的倍数，即 k*G，其中 k 是某个整数。

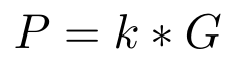
椭圆曲线的生成点。

其中：

• P — 曲线上的一个点。
• k — 整数。
• G — 生成点。

2. 单位元素

无穷远点 O 是与有限域中的加法单位元素等效的单位元素。这意味着对于曲线上的每个点，下列方程成立：

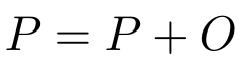
无穷远点方程。

其中：

• P — 曲线上的点。
• O — 单位元素。

3. 生成元阶

与群中元素的阶类似，椭圆曲线中生成元的阶是最大整数 n，使得与 G 乘法等于 O — 单位元素。表示为下列方程：

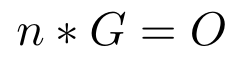
生成元的阶。

4. 曲线的阶

曲线上元素的数量，包括无穷远点，称为曲线的阶。通常用 N 表示。

5. 余因子

椭圆曲线的余因子，通常记作 h，是曲线的阶 N 与生成元的阶 n 的比率：

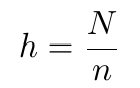
椭圆曲线的余因子。

6. 离散对数问题

离散对数问题是一个理论上非常难在椭圆曲线上解决的问题：给定点 X，生成点 G，找到有限域 F_p 中的 x，使得 x*G=X。x 通常表示为：

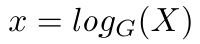
离散对数问题方程。

操作

1. 加法

给定曲线上的两个点 P、Q，操作 P+Q 返回曲线上的另一个点。

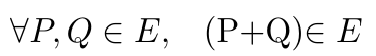
椭圆曲线上的加法操作。

2. 标量乘法

给定曲线上的点 P，与有限域 F_p 中的整数 k 的标量乘法返回曲线上的另一个点。

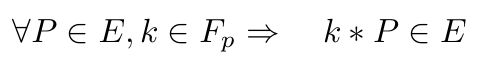
椭圆曲线上的标量乘法。

示例

让我们探讨一个在 ECDSA 签名方案中使用的标准椭圆曲线 “secp256k1”。

1. 方程

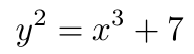
secp256k1 曲线方程。

2. 有限域

椭圆曲线在有限域 F_q 上定义，它是质数域，质数 p 如下。

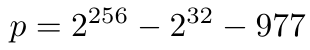
有限域的质数。

3. 生成点

G(x0,y0)，其中

• x0=55066263022277343669578718895168534326250603453777594175500187360389116729240
• y0=32670510020758816978083085130507043184471273380659243275938904335757337482424

4. 阶

生成点 G 的阶是一个大质数 n：

n=115792089237316195423570985008687907852837564279074904382605163141518161494337

5. 余因子

余因子 h=1，意味着曲线上的所有点均由基点 G 生成。

secp256k1 曲线如下图所示：

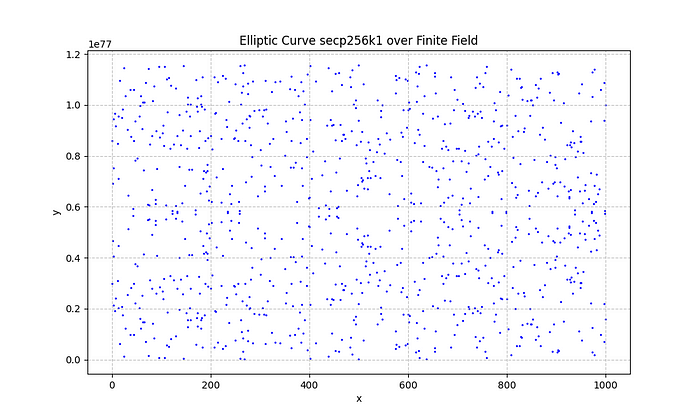
secp256k1 椭圆曲线

6. 操作

如上所述，椭圆曲线支持两种操作 加法 和 标量乘法。让我们审视这些操作的例子，用方程 G + 2G = 3G 表示，其中 G 是生成点。

首先，我们有 G=(x0, y0) 如上所述：

• x0=55066263022277343669578718895168534326250603453777594175500187360389116729240
• y0=32670510020758816978083085130507043184471273380659243275938904335757337482424

其次，我们需要计算 2G=(x1,y1) 使得：

• x1=89565891926547004231252920425935692360644145829622209833684329913297188986597
• y1=12158399299693830322967808612713398636155367887041628176798871954788371653930

计算 2G 的过程较复杂，真正值得一文详细阐述。为了避免陷入复杂的数学公式，我将这些计算留待后续文章。在此期间，如果你对这些计算感兴趣，建议阅读 这篇优秀的文章 了解 Rareskills。

接下来我们计算 3G=(x2,y2)，使得：

• x2=112711660439710606056748659173929673102114977341539408544630613555209775888121
• y2=25583027980570883691656905877401976406448868254816295069919888960541586679410

现在我们可以验证 3G 是曲线上的点，因为它满足方程 y2² = x2³ + 7，可以使用算术运算轻易验证。这意味着方程 G + 2G = 3G 成立。该操作的代码示例如下。

signature-schemes/secp256k1_ecc.py at main · 0xbarchitect/signature-schemes

配对

定义

配对是一种先进的加密操作，它将两个椭圆曲线上的点映射到目标有限域中的一个元素。概念上，把配对视为椭圆曲线上的乘法。它表示为 e。

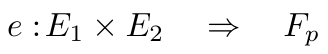
椭圆曲线配对操作。

配对可以用下图表示：

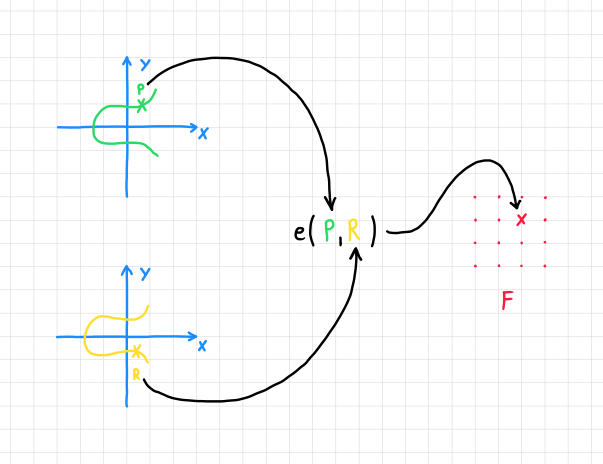
椭圆曲线配对（致谢 Philipp Muens）

双线性映射

配对具有一个 unique 属性称为 双线性映射，如下所述。

双线性映射属性。

其中：

• P, Q, R — 椭圆曲线上的点
• a, b — 整数

双线性映射意味着我们可以在曲线上“移动”系数 a, b，同时让映射结果等于 e(P, Q)^(ab)。

安全含义

将双线性映射属性应用于一个特殊情况，当：

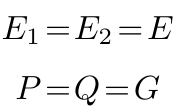
我们有：

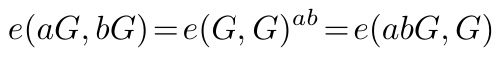
即，给定 G、aG、bG，我们可以将 abG 与随机数区分开，因为我们知道 e(abG, G) 等于 e(aG, bG) 但 e(random_number, G) 不等于 e(aG, bG)。换句话说，一旦我们拥有了配对，我们就可以解决离散对数问题（DDH）[6]，该问题指出给定 aG、bG 和 G，区分 abG 与椭圆曲线 E 上的随机点是 infeasible 的。

示例

需要注意的是，并非每条椭圆曲线都对配对友好。仅特定的椭圆曲线，例如 BN128 或 BLS12–381，才能实现配对操作。配对的双线性映射属性使得签名聚合成为可能，这在 BLS 签名方案中具有重要意义。

让我们探讨一个配对友好的椭圆曲线 — BLS12–381 曲线。BLS12–381 曲线在下图中展示。

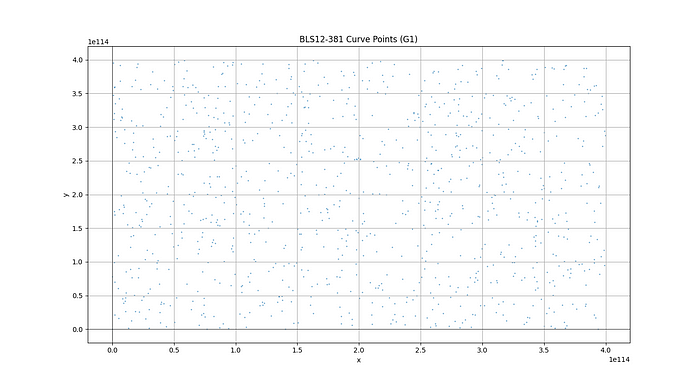
BLS12–381 椭圆曲线。

1. 方程

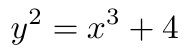
BLS12–381 曲线方程。

2. 有限域

与不适合配对的椭圆曲线（如 secp256k1 或 Curve25519）不同，BLS12–381 曲线在 2 个域上定义。

• 基域 F_q，实际上是一个质数域，质数为：

p=4002409555221667393417789825735904156556882819939007885332058136124031650490837864442687629129015664037894272559787=2³⁸¹-19

• 扩展域 F_q² 的元素类似于复数，表示为 a+bi，其中 a, b 属于 F_q，而 i 是一个虚单位，其中 i²=-1。

3. 阶

曲线上的点数量，即曲线的阶，也是一个质数：

q=52435875175126190479447740508185965837690552500527637822603658699938581184513

4. 生成点

存在 2 个生成点 G1 和 G2 对应于 2 个群。G1 群涵盖基域 F_q，而 G2 群涵盖扩展域 F_q²。

G1(x,y)

• x=3685416753713387016781088315183077757961620795782546409894578378688607592378376318836054947676345821548104185464507
• y=1339506544944476473020471379941921221584933875938349620426543736416511423956333506472724655353366534992391756441569

G2(x,y)

• x=352701069587466618187139116011060144890029952792775240219908644239793785735715026873347600343865175952761926303160 + 3059144344244213709971259814753781636986470325476647558659373206291635324768958432433509563104347017837885763365758 * i
• y=1985150602287291935568054521177171638300868978215655730859378665066344726373823718423869104263333984641494340347905 + 927553665492332455747201965776037880757740193453592970025027978793976877002675564980949289727957565575433344219582 * i

5. 配对

让我们审视 G1 和 G2 上的配对操作，其结果是有限域中的一个元素。

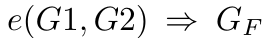
G1 和 G2 上的配对操作

配对结果：

G_F = (3408834164464458755751340723502736743445402614640994055433339214424916442641449510670327077303074893591740399366532, 1017299873256115394687936133146817339783508925356207904663165117501336940438300180831508525168135575931758510829235, 1919447955347661378578718469488414822573562393353397544098339472673901193098010131520945815709482515519580400649694, 233557331756520805040932826416017142246700002714928636467514104620558679338483625829873520553081791155104026612174, 2882199334237819327910933128503231887000342950792587449681715803095618652567681747054312179958427092970985872417068, 579878855790610229145575079003483905368886712027403088810647643659132674704592975818766405092658613973478871626949, 3268798540077874559188095304926415053902298079662269128631117894259354335713488241073281881110999874366368799440511, 2688711983546324406847903726099677850388169649284572370749691792743294691894680263880362424577638309433508620982332, 3520140447471844017044610248175793726488927385800919015247604269617056365166670232096113218155158979455637700602719, 1555267885602801620621747613743921378408444002839854792606782732724136830563310004098024452104661167182680744848589, 2626389147790168154036854297373352480470342009417426750876875476996308393122833154115295241935326582225976246741447, 873321072950766150592434764742436722571574260472569072177205897167854308426485977134306337249021436737462538398830)

配对结果表示为一组大整数，作为扩展域中结果元素的系数。该操作的代码示例如下。

bls12_381_pairing.py

结论

我们讨论的高级加密原语是设计和实现许多高级协议（如数字签名方案、多方计算（MPC）和零知识证明（ZKP））的基石。希望本文能帮助你建立扎实的基础知识，为你在密码学中取得成功做出贡献。观察这些原语在实践中的应用非常有趣，接下来我们将讨论高级加密协议。敬请关注！

如果你觉得这篇文章对你有启发，请关注我。这将让我非常开心，并激励我写更多高质量的文章。非常感谢你的支持🙏

参考文献

1. [Nguyen Thoi Minh Quan — 直观的高级加密]
2. [Philipp Muens — ECDSA 算法]
3. [RareSkills — ECDSA 背后的直观理解]
4. [Andrea Corbellini — ECDH 与 ECDSA]
5. [维基百科 — 椭圆曲线密码学]
6. [维基百科 — Diffie-Hellman 问题]
7. [RareSkills — 椭圆曲线加法]

• 原文链接： medium.com/@barchitect/a...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～