椭圆曲线点加法

这篇文章描述了椭圆曲线在实数上的加法是如何工作的。

加密技术使用有限域上的椭圆曲线，但在实数的笛卡尔平面上理解椭圆曲线要简单得多。本文面向程序员，力求在较多数学内容与较轻松讨论之间找到一个平衡。

椭圆曲线的集合论定义

椭圆曲线上的点集在椭圆曲线点加法下形成一个群。

希望如果你已经阅读了我们的群论介绍，你实际上能够理解大部分内容，除了“点加法”是什么。但这就是抽象代数的美妙之处，对吧？你无需知道那是什么，依然可以理解上述句子。

椭圆曲线是一类具有如下公式的曲线：

$$ y^2 = x^3 + ax + b $$

根据你选择的 a 和 b 的值，你将得到如以下的一些曲线：

在椭圆曲线上，一个点是一个满足 $y² = x³ + ax + b$ 的 $(x, y)$ 对，给定特定的 a 和 b。

例如，点 $(3, 6)$ 在曲线 $y² = x³ + 9$ 上，因为 $6² = 3³ + 9$。在群论的术语中，$(3, 6)$ 是由 $y² = x³ + 9$ 定义的集合的一个成员。因为我们处理的是实数，这个集合具有无限的基数。

这里的想法是，我们可以从这个集合中取出两个点，应用一个二元运算，然后我们将得到另一个同样在该集合中的点。也就是说，它是一个也在曲线上的 $(x, y)$ 对。

不要试图将椭圆曲线视为图上的一个图形，而是将其视为一个无限的点集。只有当且仅当满足椭圆曲线方程时，点才在这个集合中。

一旦我们将这些点视为一个集合，以群的形式看待它并不神秘。我们只需取两个点，并根据群的规则生成第三个。

具体来说，要成为一个群，点集合需要具备：

• 一个闭合和结合的二元运算，即它会在该集合中生成另一个点
• 该集合必须有一个单位元素 $I$
• 集合中的每个点必须有一个逆元素，使得当两者与二元运算结合时，结果是 $I$

椭圆曲线在加法下形成阿贝尔群

虽然我们并不知道二元运算如何工作，但我们知道它需要两个在曲线上的 $(x, y)$ 点，并返回曲线上的另一个点。因为运算是封闭的，我们知道这个点实际上是椭圆曲线方程的有效解，而不是其他地方的一个点。

我们也知道这个二元运算是结合的（根据章节标题的内容，也是可交换的）。

所以给定椭圆曲线上的三个点 $A$、$B$ 和 $C$ （或者 $(x_a, y_a)$、$(x_b, y_b)$ 和 $(x_c, y_c)$，如果你喜欢的话），我们知道以下内容是正确的：

• $(A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)$
• $A ⊕ B = B ⊕ A$

我使用 $⊕$，因为我们知道这个二元运算在任何正常意义下都不是加法，而是一个二元运算（再次提醒，根据集合论，二元运算接收集合中的两个元素，并返回集合中的其他元素，它是如何做到这一点的，不是定义的核心）。

我们也知道必须存在某个位置的单位元素。即，任何落在曲线上的 $(x, y)$ 点与单位元素结合时，输出的仍然是相同的不变的 $(x, y)$ 点。

而且因为这是一个群而不是一个幺半群，所以每个点都需要有一个逆元素，使得 $P ⊕ P⁻¹ = I$，其中 $I$ 是单位元素。

单位元素( identity element)

直观上我们可能会认为 $(0, 0)$ 或者 $(1, 1)$ 是单位元素，因为这些值在其他群中往往是这样的，但是你可以在上面的图中看到，这些点通常不落在曲线上。因为它们不属于集合 $y² = x³ + ax + b$ 上的点，它们不是该群的一部分。

但是请记住，根据集合论，我们可以任意定义二元运算。这使我们能够添加一个技术上不在曲线上的特殊元素，但根据定义它是单位元素。

我喜欢将单位元素视为“无处的点”，因为如果你将无处与任何实数点结合，则什么都不会改变。恼人的是，数学家将这个点，称为“无穷远的点”。

嘿，等等，这点不是应该满足 $y² = x³ + ax + b$ 吗？无处（或无穷大）并不是 $(x, y)$ 的有效值。

啊，但请记住，我们可以任意定义集合！我们将构成椭圆曲线的集合定义为椭圆曲线上的点和无处点。

因为二元运算仅仅是笛卡尔乘积的子集（一种关系），我们可以随意定义这个关系。我们可以在我们的算术中有任意多的“如果语句”，并且仍然遵循群法则。

加法是封闭的

不失一般性，让我们取椭圆曲线

$$ y² = x³ + 10 $$

以说明直线如何与椭圆曲线相交，让我们绘制一条几乎竖直的直线 $y = 10x$

（它可以是 1000x 以使其更加竖直，但我们会得到数值不稳定性，正如你将在后面看到的那样）

我们得到以下的一组图示。

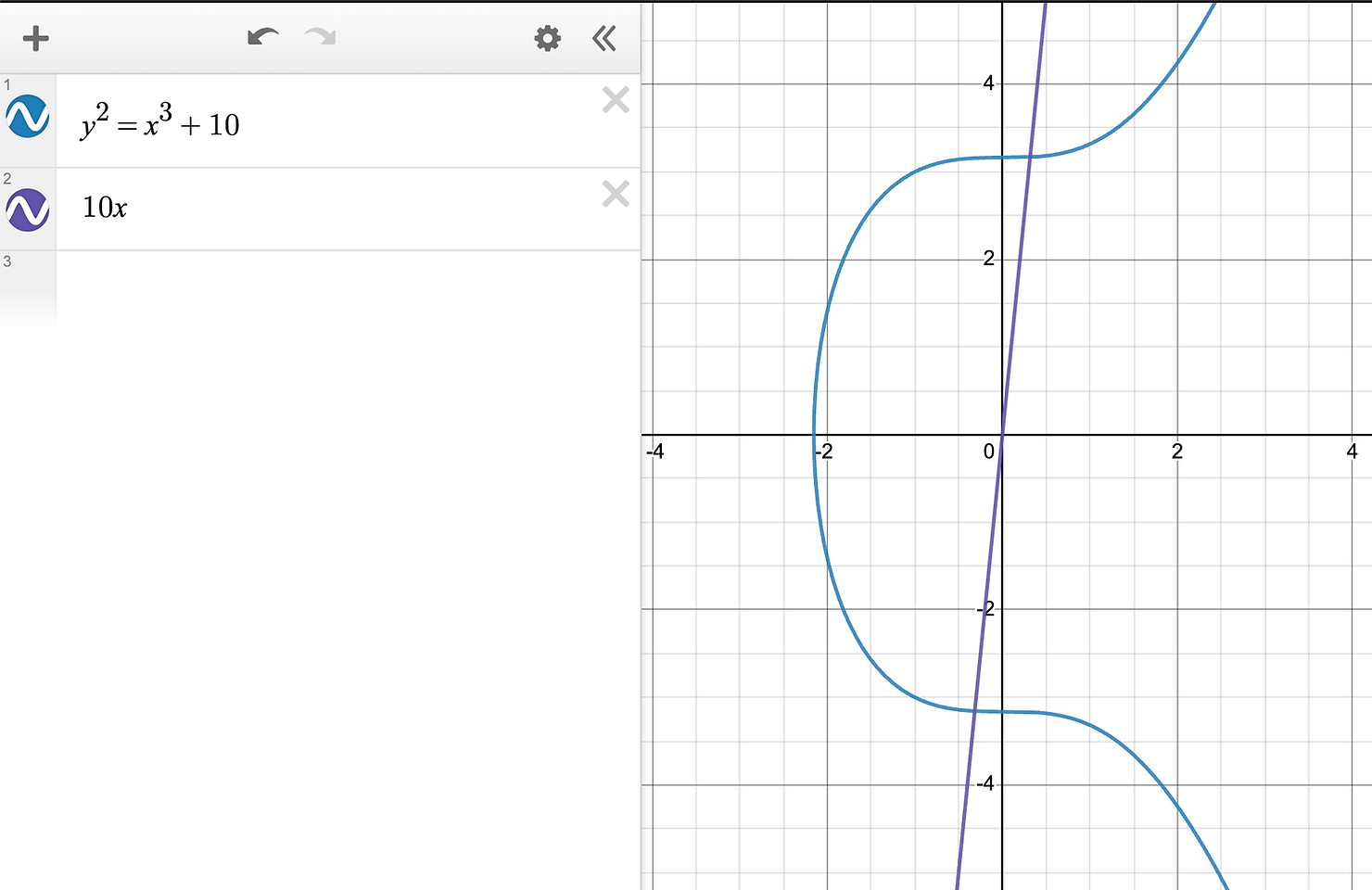
事实证明，即使看起来紫色线条（$y = 10x$）的上升速度比蓝色曲线（$y² = x³ + 10$）快，但它们总会相交。

如果我们放大到足够的程度，我们可以看到交点。这在一般情况下是成立的。

只要 x 不是“完全竖直”的，只要它与曲线的两个点交叉，它总会再次交叉第三个点。 那两个点如果是切点，则这两个点可能是同一个点。

“如果我们与两个点相交”很重要。如果我们将紫线向左移动，以便它不穿过椭圆曲线的“U型”，那么它只会在一个点相交。

理解这一点的另一种方法：

如果一条直线在椭圆曲线上恰好相交两个点，并且没有交点是切线交点，那么它必须是完全竖直的。

你可以从上面的公式中进行代数证明，但我认为几何上的论述更直观。

我建议你停下来并绘制一些椭圆曲线和直线，以视觉上说服自己。

我们对垂直线的例外实际上会使逆元素和单位元素完美契合。

椭圆曲线上一个点的逆是该对的 y 值的负值。 也就是说，$(x, y)$ 的逆是 $(x, -y)$，反之亦然。通过这样的点绘制一条直线会形成一条完美的竖直线。

我们之前提到的“无穷远”的点就是我们之前提到的单位元素，当我们绘制一条垂直线时，它就是“高高在上”的点。

阿贝尔群

椭圆曲线点在我们的“2 个点总是产生一个第三个点，除非是单位”的背景下，显然具有可交换性质。

当我们选择两个点时，只有一个唯一的第三个点。你不能在椭圆曲线上得到四个交点。因为我们只得到一个可能的解，所以显然 $A ⊕ B = B ⊕ A$。

为什么椭圆曲线加法在$x$轴上翻转

我们在上一节中忽略了一个非常重要的细节，因为它确实值得一个单独的章节。

在目前的形式下，如果我们两点相加而相交在中间，它就存在缺陷。

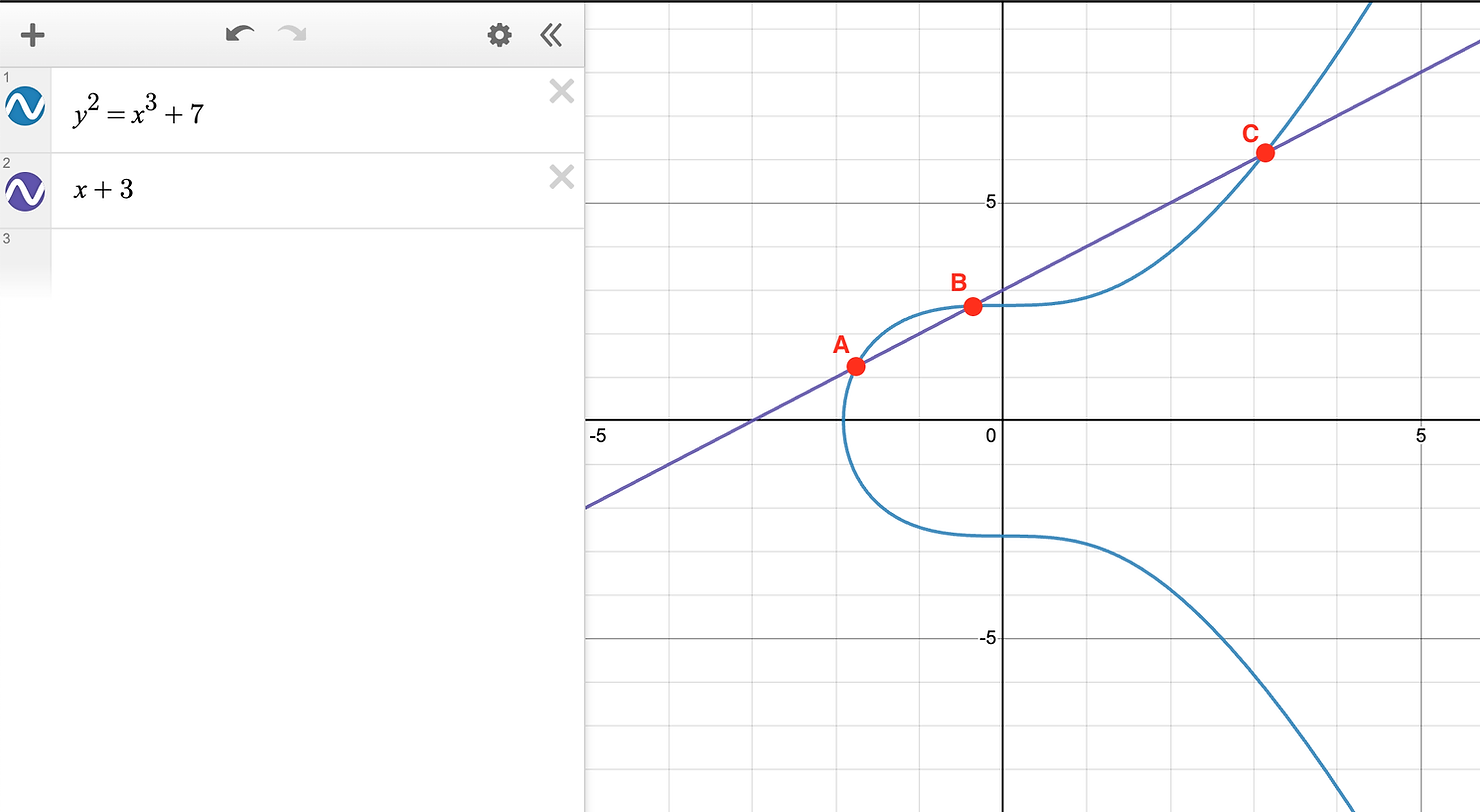
根据我们上面的定义，以下内容必须成立：

$$ \begin{align} A ⊕ B &= C \\ A ⊕ C &= B \\ B ⊕ C &= A \end{align} $$

通过一些代数，我们可以推导出矛盾：

$$ \begin{align} (B ⊕ C) ⊕ B &= C \\ B ⊕ C &= \mathsf{inv}(B) ⊕ C \\ B &= \mathsf{inv}(B) \end{align} $$

这句话意味着 $B$ 等于其逆元。但是 $B$ 不是单位元（只有单位元素才可能是其自身的逆），因此我们有了一个矛盾。

幸运的是，我们可以通过一种方法来挽救这一点。只需将点加法定义为第三点 翻转到 y 轴。再次强调，我们 被允许这样做，因为二元运算可以以我们喜欢的方式定义，我们只需要确保我们的定义满足群法则。

因此，正确的方式来添加椭圆曲线点在图上表示如下：

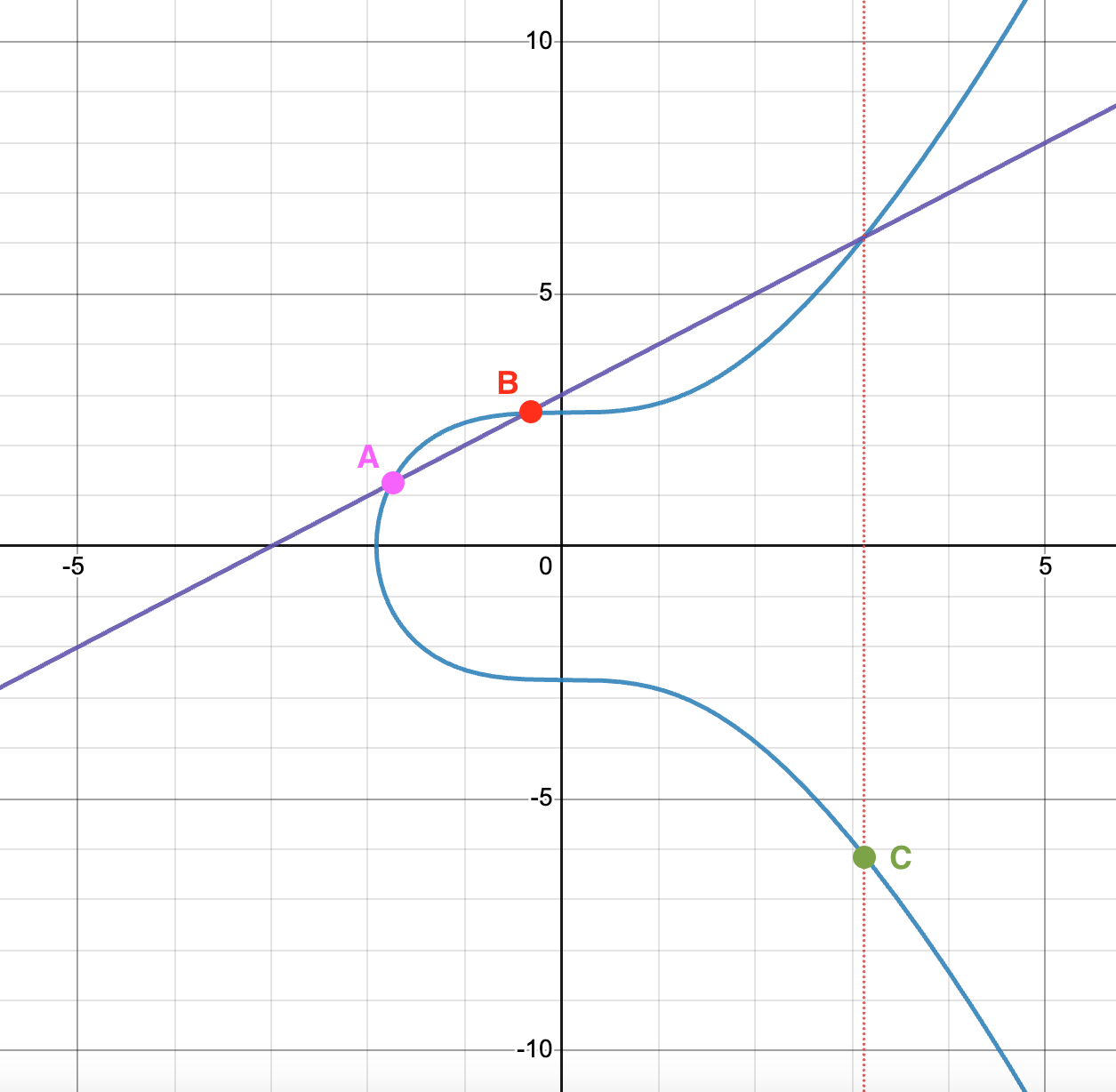
加法公式

通过一些代数，给定两个点

$$ \begin{align} P₁ &= (x₁, y₁) \\ P₂ &= (x₂, y₂) \end{align} $$

可以推导出如何计算 $P₃ = (x₃, y₃)$，其中 $P₃ = P₁ ⊕ P₂$，使用如下公式。

$$ \begin{align} \lambda &= \frac{y₂ – y₁}{x₂ – x₁} \\ x₃ &= \lambda² – x₁ – x₂ \\ y₃ &= \lambda(x₃ – x₁) – y₁ \end{align} $$

代数演示可交换性和结合性

由于我们有一个封闭形式的方程，我们可以在给定点 $T$ 和 $U$ 的情况下证明 $T⊕U = U⊕T$。

我们这样做：

$$ \begin{align} P &= T ⊕ U \\ Q &= U ⊕ T \\ P &= Q \end{align} $$

var('y_t', 'y_u', 'x_t', 'x_u')
lambda_p = (y_u - y_t)/(x_u - x_t)
x_p = lambda_p^2 - x_t - x_u
y_p = (lambda_p*(x_t - x_p) - y_t)

lambda_q = (y_t - y_u)/(x_t - x_u)
x_q = lambda_q^2 - x_u - x_t
y_q = (lambda_q*(x_u - x_q) - y_u)

下面是运行上述代码在 Jupyter notebook 的截图并美观打印输出。计算机代数系统需要一些调整，但我们可以明显看到 x_q == x_p 和 y_q == y_p。

对于所有 $(x_t, y_t)$ 和 $(x_u, y_u)$ 值我们都有 $P = Q$ 的成立。如果 $x_t = x_u$，我们会得到一个零除错误...