zk-SNARKs 可行性的大致介绍

An approximate introduction to how zk-SNARKs are possible

特别感谢 Dankrad Feist、Karl Floersch 和 Hsiao-wei Wang 对反馈和评审的支持。

也许过去十年中最强大的加密技术是通用的简洁零知识证明，通常称为 zk-SNARKs（“零知识简洁论证”）。一个 zk-SNARK 允许你生成一个证明，表明某些计算有某个特定输出，这种证明可以被极快速地验证，即便基础计算需要很长时间才能完成。“ZK”（“零知识”）部分增加了一个额外的特性：证明可以隐藏输入计算的一些部分。

例如，你可以为以下陈述生成证明：“我知道一个秘密数字，使得如果你将单词‘cow’放在后面，再进行 1 亿次 SHA256 哈希，输出的开头是 0x57d00485aa。”验证者可以迅速验证这个证明，而无需自己进行 1 亿次哈希，证明也不会泄露秘密数字是什么。

在区块链的背景下，这有两个非常强大的应用：

1. 可扩展性：如果一个区块验证耗时较长，则一个人可以验证它并生成证明，而其他人只需快速验证证明即可。
2. 隐私：你可以证明你有权转移某项资产（你收到了它，且没人已经转移它），而无需透露你收到了哪项资产。这确保了安全性，同时不使公众过度了解谁与谁进行交易。

但是 zk-SNARKs 相当复杂；事实上，直到 2014-17 年，它们仍然常被称作“月亮数学”。好消息是，从那时起，协议变得更简单，我们对它们的理解也大大提高。本文将试图以一种普通人能够理解的方式解释 zk-SNARKs 工作原理，前提是读者具备中等程度的数学基础。

请注意，我们将重点关注可扩展性；这些协议的隐私实际上相对简单，一旦可扩展性得以实现，最后我们会再回到这个话题上。

为什么 zk-SNARKs “应该” 是困难的

让我们以我们开始的例子为例：我们有一个数字（我们可以将“cow”及其后面的秘密输入编码为一个整数），我们计算该数字的 SHA256 哈希，然后再计算另外 99,999,999 次，我们得到输出，然后检查它的起始数字。这是一个 巨大的 计算。

“简洁”证明是指证明和验证所需时间远比要验证的计算增长得慢。如果我们想要一个“简洁”的证明，我们不能要求验证者在每轮哈希中做一些工作（因为那样验证时间将与计算成正比）。相反，验证者必须以某种方式检查整个计算，而不查看每个单独的计算部分。

一个自然的技术是 随机抽样 : 如果我们让验证者在计算中检查 500 个不同的位置，检查这些部分是否正确，如果所有 500 次检查都通过，那么就假设其余的计算在很高的概率下也应该是好的，这怎么样？

这样一个程序甚至可以使用 Fiat-Shamir 启发式 转换为非交互式证明：证明者计算出计算的 Merkle 根，使用 Merkle 根随机选择 500 个索引，并提供相应的 500 个 Merkle 分支。关键在于，证明者不知道他们需要揭示哪些分支，直到他们已经“承诺”数据。如果一个恶意证明者在得知哪些索引要被检查后试图改变数据，必然会改变 Merkle 根，这将导致生成一组新的随机索引，并需要重新捏造数据……这将恶意证明者困在一个无尽的循环中。

但不幸的是，以这种方式直接应用随机抽样检查计算存在一个致命缺陷：计算本质上是 脆弱 的。如果一个恶意证明者在计算的某个部分翻转了一位，他们可以使计算给出完全不同的结果，而随机抽样的验证者几乎永远不会发现。

__

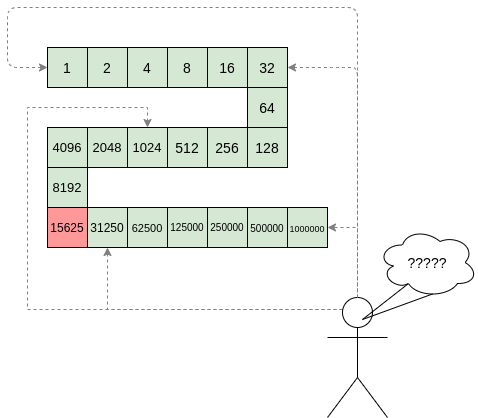
如果 要设计 zk-SNARK 协议，许多人可能会走到这个地步然后被卡住并放弃。一个验证者怎么可能在不查看每个计算部分的情况下检查每个单独部分的计算呢？但事实证明，有一个巧妙的解决方案。

多项式

多项式是一类特殊的代数表达式，其形式为：

• x+5
• x4
• x3+3x2+3x+1
• 628x271+318x270+530x269+...+69x+381

也就是说，它们是以 cxk 的形式的有限数目的项之和。

关于多项式有许多令人着迷的东西。但在这里，我们将专注于一个特定的点：多项式是一种单一的数学对象，可以包含无界数量的信息（将其视为整数列表，很容易理解）。上面的第四个示例包含了 816 位的 tau，人们可以轻易想象出一个包含更多的多项式。

此外，一个关于多项式的单一方程可以表示无界数量的关于数字的方程。例如，考虑方程 A(x)+B(x)=C(x)。如果这个方程是正确的，那么也意味着：

• A(0)+B(0)=C(0)
• A(1)+B(1)=C(1)
• A(2)+B(2)=C(2)
• A(3)+B(3)=C(3)

依此类推，对每一个可能的坐标也成立。你甚至可以构造多项式，以蓄意表示数字的集合，这样你可以同时检查许多方程。例如，假设你想要检查：

• 12 + 1 = 13
• 10 + 8 = 18
• 15 + 8 = 23
• 15 + 13 = 28

你可以使用一个名为 Lagrange 插值 的过程来构造多项式 A(x)，使其在某些特定坐标（例如 (0, 1, 2, 3)）输出 (12, 10, 15, 15)，而 B(x) 在相同坐标上的输出为 (1, 8, 8, 13)，以此类推。事实上，以下是这些多项式：

• A(x)=-2x3+192x2−192x+12
• B(x)=2x3−192x2+292x+1
• C(x)=5x+13

用这些多项式检查方程 A(x)+B(x)=C(x，同时检查上述四个方程。

将多项式与其自身进行比较

你甚至可以使用一个简单的多项式方程检查大量的 相邻同样多项式 的评估之间的关系。这稍微更高级一点。假设你想要检查，对于给定的多项式 F，F(x+2)=F(x)+F(x+1) 在整数范围 {0,1...98} 内成立（所以如果你 也 检查 F(0)=F(1)=1，那么 F(100) 将是第 100 个 斐波那契数）。

作为多项式，F(x+2)−F(x+1)−F(x) 将不会完全为零，因为它在范围 x={0,1...98} 之外会给出任意的答案。但是我们可以做一些巧妙的事。一般来说，有一个规则：如果多项式 P 在某个集合 S={x1,x2...xn} 上为零，则可以表示为 P(x)=Z(x)∗H(x)，其中 Z(x)= (x−x1)∗(x−x2)∗...∗(x−xn)，H(x) 也是多项式。换句话说，任何在某个集合上等于零的多项式都是等于该集合上零的最简单（最低度）多项式的（多项式）倍数。

为什么会这样？这是多项式长除法的一个很好推论：因子定理。我们知道，当将 P(x) 除以 Z(x) 时，我们会获得一个商 Q(x) 和一个余数 R(x)，满足 P(x)=Z(x)∗Q(x)+R(x)，其中余数 R(x) 的次数严格小于 Z(x)。因为我们知道 P 在 S 的所有位置为零，所以 R 在 S 的所有位置也必须为零。因此，我们可以简单地通过多项式插值计算 R(x)，因为它是至多 n−1 次的多项式，而我们知道 n 个值（在 S 处的零点）。插值一个零点完全给出零多项式，因此 R(x)=0，H(x)=Q(x)。

回到我们的例子，如果我们有一个编码了斐波那契数的多项式 F（例如 F(x+2)=F(x)+F(x+1) 在 x={0,1...98} 上成立），那么我可以向你证明，F 实际上满足这个条件，通过证明多项式 P(x)= F(x+2)−F(x+1)−F(x) 在此范围内为零，通过提供商：

H(x)=F(x+2)−F(x+1)−F(x)Z(x)

其中 Z(x)=(x−0)∗(x−1)∗...∗(x−98)。

你可以自己计算 Z(x)（理想情况下你应该将它预先计算好），检查方程，如果检查通过，那么 F(x) 就满足这个条件！

现在，退后一步，注意我们在这里做了什么。我们将一个 100 步长的计算（计算第 100 个斐波那契数）转换为一个多项式的单一方程。当然，证明 N’th 斐波那契数并不是一项特别有用的任务，尤其是对于那些 有闭式表达 的斐波那契数。但你可以简单使用相同的基本技术，只需额外的多项式和更复杂的方程，就可以编码任意计算，且包含任意数目的步骤。

现在，如果只有一种方法可以比逐个检查每个系数更快地验证多项式之间的方程…

多项式承诺

然后，再次，事实证明有答案：多项式承诺。多项式承诺最好视为一种特殊的“哈希”多项式的方式，其中哈希具有额外的特性，即可以通过检查多项式之间的哈希之间的方程来检查多项式之间的方程。不同的多项式承诺方案在可以检查哪些类型的方程方面具有不同的特性。

以下是一些常见示例，通过各种多项式承诺方案可以完成的操作（我们用 com(P) 来表示“多项式 P 的承诺”）：

• 相加：给定 com(P)、com(Q) 和 com(R)，检查 P+Q=R
• 相乘：给定 com(P)、com(Q) 和 com(R)，检查 P∗Q=R
• 在某一点上求值：给定 com(P)、w、z 和补充证明（或“见证”）Q，验证 P(w)=z

值得注意的是，这些原语可以相互构造。如果你可以添加和相乘，那么你可以评估：为了证明 P(w)=z，你可以构造 Q(x)=P(x)−zx−w，验证者可以检查 Q(x)∗(x−w)+z=?P(x)。这行得通，因为如果这样的多项式 Q(x) 存在 ，那么 P(x)−z=Q(x)∗(x−w)，这意味着 P(x)−z 在 w 处等于零（因为 x−w 在 w 处等于零），因此 P(x) 在 w 上等于 z。

如果你可以评估，你可以进行各种检查。这是因为有一个 数学定理，大致上说明了如果某个涉及多项式的方程在一个 随机选择的坐标 上成立，那么它几乎肯定在整体多项式上也成立。因此，如果我们只有证明评估的机制，我们可以检查，例如我们的方程 P(x+2)−P(x+1)−P(x)=Z(x)∗H(x)，使用一个交互式游戏：

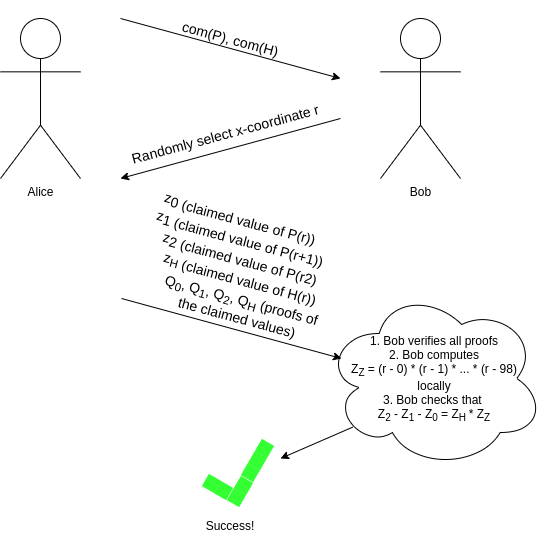
正如我之前提到的，我们可以使用 Fiat-Shamir 启发式 将其转变为非交互式：证明者可以通过设置 r = hash(com(P), com(H)) 自行计算 r （其中 hash 是任何加密哈希函数；它不需要任何特殊的属性）。证明者无法通过选择在特定 r 下“契合”但在其他地方不契合的 P 和 H 来“作弊”，因为他们在选择 P 和 H 时并不知道 r！

到此为止的快速回顾

• ZK-SNARKs 很难，因为验证者需要以某种方式检查计算中的数百万个步骤，而不会直接对每个步骤进行一项工作（因为那样会太慢）。
• 我们通过将计算编码成多项式来绕过这个问题。
• 一个多项式可以包含无界的大量信息，一个多项式表达式（例如 P(x+2)−P(x+1)−P(x)=Z(x)∗H(x)）可以“替代”无界数量的数字方程。
• 如果你可以通过多项式验证方程，你就隐式地同时验证所有的数字方程（将 x 替换为任何实际的 x 坐标）。
• 我们使用一种特殊类型的多项式的“哈希”，称为 多项式承诺，以便让我们实际上能以非常短的时间验证多项式间的方程，即使基础多项式非常大。

那么，这些华丽的多项式哈希是如何工作的？

目前有三种广泛使用的主要方案：bulletproofs、Kate 和 FRI。

• 这是 Dankrad Feist 对 Kate 承诺的描述：<https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html>
• 这是 curve25519-dalek 团队对 bulletproofs 的描述：<https://doc-internal.dalek.rs/bulletproofs/notes/inner_product_proof/index.html>，还有我对它的解释：&lt;https://twitter.com/VitalikButerin/status/1371844878968176647>
• 这是我对 FRI 的描述：../../../2017/11/22/starks_part_2.html

哇，慢点来。尝试简单解释其中一个，而不是继续发送我去更可怕的链接

老实说，它们并没有 那么 简单。这也是为何这些数学在 2015 年之前并没有真正获得重视的原因。

可以吗？

依我看，最容易完全理解的是 FRI（如果你愿意接受 椭圆曲线配对 作为“黑盒”，那么 Kate 更容易，但配对 真的 很复杂，因此总的而言，我觉得 FRI 更简单）。

以下是简化版 FRI 工作方式的描述（真实协议在此处缺少许多技巧和优化以简化）。假设你有一个次数小于 n 的多项式 P。对 P 的承诺是对某一组预选坐标（例如 {0,1....8n-1}，尽管这不是最有效的选择）的一组对 P 的评估的 Merkle 根。现在，我们需要添加一些额外的东西，以证明这组评估实际上是一个次数小于 n 的多项式。

令 Q 为仅包含 P 的偶系数的多项式，R 为仅包含 P 的奇系数的多项式。因此，如果 P(x)=x4+4x3+6x2+4x+1，那么 Q(x)=x2+6x+1，而 R(x)=4x+4 （注意，系数的次数被“压缩”到 [0...n2] 范围）。

请注意 P(x)=Q(x2)+x∗R(x2)（如果这对你来说不太明显，停下来看一看示例直至你理解）。

我们要求证明者提供 Q(x) 和 R(x) 的 Merkle 根。然后，我们生成一个随机数 r 并要求证明者提供一个“随机线性组合” S(x)=Q(x)+r∗R(x)。

我们随机抽取一大组索引（使用前面提供的 Merkle 根作为随机性的种子），并要求证明者为 P、Q、R 和 S 在这些索引处提供 Merkle 分支。在每个提供的坐标处，我们检查：

• P(x) 实际上等于 Q(x2)+x∗R(x2)
• S(x) 实际上等于 Q(x)+r∗R(x)

如果我们进行足够多的检查，我们可以确信，S(x) 的“预期值”在最大 1% 的情况下与“提供的值”不同。

请注意 Q 和 R 的次数均小于 n2。由于 S 是 Q 和 R 的线性组合，S 也 具有次数小于 n2。反过来，如果我们证明 S 的次数小于 n2，那么它是随机组合的，则证明者无法选择隐藏高次系数的恶意 Q 和 R，因此 Q 和 R 的次数都必须小于 n2，且由于 P(x)=Q(x2)+x∗R(x2)，我们知道 P 的次数必须小于 n。

接下来，我们简单地重复这一过程，用 S 逐渐“降低”我们关心的多项式的次数，直到它低到我们可以直接检查的程度。

和前面相似，这里“Bob”是一个抽象概念，有助于密码学家理解协议。实际上，Alice 正在生成整个证明，为了防止其作弊，我们使用 Fiat-Shamir：我们依据在此之前生成的证明数据的哈希值选择每个随机抽样坐标或 r 值。

对 P 的完整 “FRI 承诺” （在此简化协议中）将包括：

1. P 的评估的 Merkle 根
2. Q、R、S1 的评估的 Merkle 根
3. 在检查 S1 是否正确从 P “化简”的情况下随机选择的 P、Q、R、S1 的分支
4. 在步骤（2）和（3）中对于从 S1 化简到 S2，从 S2 化简到 S3 的所有乘法的 Merkle 根与随机选择的分支，直到最后得到一个低度 Sk （这一过程总计重复 ≈log2(n) 次）
5. Sk 的评估的完整 Merkle 树（以便我们可以直接检查）

该过程中的每一步可能引入“错误”，但只要增加足够的检查，总体错误就会低到可以在 80% 的位置至少证明 P(x) 等于一个次数小于 n 的多项式。这对于我们的用例是足够的。如果你想在 zk-SNARK 中作弊，你需要为一个分式表达式生成一个多项式承诺（例如，“证明” x2+2x+3 在 4 的值为 5，你需要为 x2+2x+3−5x−4=x+6+22x−4 提供多项式承诺）。这样的分式表达式的评估将与任何真实的次数小于 n 的多项式在多个位置上 不同，因此进行 FRI 承诺时，必然会在某个步骤失败。

此外，你可以仔细检查 FRI 承诺中对象的总数量和大小与次数之间是对数关系，因此对于大型多项式，承诺比多项式本身小得多。

要检查这种类型的不同多项式承诺之间的方程（例如，检查 A(x)+B(x)=C(x)，给定 A、B 和 C 的 FRI 承诺），只需随机选择多个索引，要求证明者在每个索引处提供 Merkle 分支，并验证该方程在每个位置确实成立。

上述描述是一个效率极低的协议；还有一整套代数技巧可以将其效率提高好几倍，如果你希望该协议在区块链交易中实际上可行，你需要这些技巧。特别是，例如，Q 和 R 并非实际上是必要的，因为如果你非常聪明地选择你要评估的点，那么你可以直接从 P 的评估重构所需的 Q 和 R 的评估。然而，上述描述应该足以让你确信多项式承诺是从根本上可能的。

有限域

在以上的描述中，有一个隐藏假设，就是每个多项式的“评估”都是小的。但是当我们处理大的多项式时，显然这一点并不成立。如果我们取上面的例子，628x271+318x270+530x269+...+69x+381，这编码了 816 位的 tau，并在 x=1000 时进行评估，你会得到……一个包含所有这些 tau 位的 816 位数字。因此我们还需要添加一个东西。实际上，在实现中，所有的运算并不会采用“常规”的实数算术，相反，它会使用 模运算。

我们重新定义所有的算术运算如下。我们选择一些素数“模数” p。% 运算符表示“取余数”：15 % 7=1，53 % 10=3，等等（请注意，答案总是非负的，因此例如 -1 % 10=9）。我们重新定义：

x+y⇒(x+y) % p

x∗y⇒(x∗y) % p

xy⇒(xy) % p

x−y⇒(x−y) % p

x/y⇒(x∗yp−2) % p

上述规则都是自洽的。例如，如果 p=7，那么：

• 5+3=1（因为 8 % 7=1）
• 1−3=5（因为 -2 % 7=5）
• 2⋅5=3
• 3/5=2（因为 (3⋅55) % 7=9375 % 7=2）

更复杂的恒等式，例如分配律也成立：(2+4)⋅3 和 2⋅3+4⋅3 评估为 4。甚至像 (a2−b2) = (a−b)⋅(a+b) 这样的公式在这个新类算术中仍然是正确的。

除法是最难的一部分；我们不能使用常规除法，因为我们希望值总是保持为整数，并且常规除法通常会给出非整数结果（例如3/5）。我们通过 费马小定理 避免了这个问题，该定理说明对于任何非零的 x<p，xp−1 % p=1。这意味着 xp−2 返回一个数，如果再乘以 x 会得到 1，所以我们可以说 xp−2（这是整数）等于 1x。一种更加复杂但是更快的评估这个模除法运算符的方法是 扩展欧几里得算法，在 Python 中的实现 这里。

通过模运算，我们创造了一个全新的算术系统，它在所有与传统算术的自洽性方面都是自洽的。因此，我们可以在这个域上讨论与“常规数学”相关的所有类型的结构，包括多项式。密码学家们喜欢在模运算（或更普遍的“有限域”）中工作，因为在那里数值的大小始终受到约束 - 无论你做什么，这些值都不会“逃脱”集合 {0,1,2...p−1}。即使在有限域中评估一个次数为 100 万的多项式也决不会给出超出该集合的答案。

有什么稍微更有用的计算被转换为一组多项式方程的例子吗？

假设我们想证明，对于某个多项式 P，0≤P(n)<264，而不透露 P(n) 的确切值。在区块链交易中，这是一种常见用例，其中你希望证明一笔交易留给余额为非负，而不透露这个余额是多少。

我们可以通过以下多项式 方程构造一个证明（为了简单起见，假设 n=64）：

• P(0)=0
• P(x+1)=P(x)∗2+R(x) 在范围 {0...63} 内
• R(x)∈{0,1} 在范围 {0...63} 内

后两个语句可以重述为“纯”多项式方程如下（在这种情况下 Z(x)=(x−0)∗(x−1)∗...∗(x−63)）：

• P(x+1)−P(x)∗2−R(x)=Z(x)∗H1(x)
• R(x)∗(1−R(x))=Z(x)∗H2(x)（注意一个巧妙的技巧：y∗(1−y)=0 当且仅当 y∈{0,1}）

这个想法是，P(i) 的连续评估逐位构建该数字：如果 P(4)=13，则直到该点的评估序列将是：{0,1,3,6,13}。在二进制中，1 是 1，3 是 11，6 是 110，13 是 1101；注意如何 P(x+1)=P(x)∗2+R(x) 持续在末尾添加一位，只要 R(x) 为零或一。在 0≤x<264 的范围内，任何数字都可以通过这样的 64 步构建，而任何超出该范围的数字则不能进行。

隐私

但是还有一个问题：我们如何知道对 P(x) 和 R(x) 的承诺会不会“泄露”信息，允许我们查明确切的 P(64) 的值，这是我们想要保密的？

好消息是：这些证明都是小证明，可以表明大量数据和计算的状况。因此一般来说，证明通常是 不会大到 泄露比一些信息更多的信息。但我们能从“只是一些”转换为“零”吗？幸运的是，我们可以。

这里，一个相当通用的技巧是将一些“干扰因素”添加到多项式中。当我们选择 P 时，为多项式中添加 Z(x) 的一个小整数倍（即，将 P′(x)=P(x)+Z(x)∗E(x) 且某个随机 E(x)）。这样做并不会影响陈述的正确性（实际上，在“正在进行计算”的坐标上，P′ 的输出与 P 的输出相同，所以它仍然是有效的记录），但可能在承诺中加入额外的“噪声”，以便剩余信息无法恢复。此外，在 FRI 的情况下，重要的是不要在“计算进行”的域内随机抽取点（在这种情况下为 {0...64}）。

我们能再回顾一次吗？

• 三种最主要的多项式承诺类型是 FRI、Kate 和 bulletproofs。
• Kate 在概念上是最简单的，但依赖于非常复杂的椭圆曲线配对的“黑盒”。
• FRI 很酷，因为它仅依赖于哈希；它通过逐步降低多项式的次数来成功工作，并通过 Merkle 分支进行随机样本检查以证明每一步的等价性。
• 为了防止单个数值的大小飙升，而不是对整数进行多项式运算，我们对有限域进行所有运算（通常是整数以某些素数 p 取模）。
• 多项式承诺自然适用于隐私保护，因为证明已经远低于多项式，因此多项式承诺无法泄露多于多项式中某些信息的更多信息。但是我们可以在承诺的多项式中添加一些随机噪声，以减少信息从“一点点”泄露到“零”的程度。

还有哪些研究问题正在被深入研究？

• 优化 FRI：已存在多种优化方案，包括对评估域的仔细选择，“DEEP-FRI”等以及大量其他技巧，以提高 FRI 的效率。Starkware 和其他人都在这里努力。
• 更好的方式来将计算编码成多项式：弄清楚将涉及哈希函数、内存访问和其他特征的复杂计算以最有效的方式编码成多项式方程仍然是一个挑战。这方面取得了很大进展（例如，参见 PLOOKUP），但我们仍需更多，尤其是如果我们希望将通用虚拟机执行编码成多项式时。
• 递增可验证计算：在计算持续进行的同时，能够有效地“扩展”证明将是非常有用的。这在单一证明人的情况下十分有价值，在多证明人情况中，也尤其是在区块链中，不同的参与者生成每一个区块。请参考 Halo 有关此方面的近期研究。

我想了解更多！

我的资料

• STARKs: 第一部分，第二部分，第三部分
• 将计算编码成多项式的具体协议：PLONK
• 一些我在这里没有提到的关键数学优化：快速傅里叶变换

其他人的资料

• Starkware 的在线课程
• Dankrad Feist 论 Kate 承诺
• Bulletproofs

• 原文链接： vitalik.eth.limo/general...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～