Curve StableSwap中的get D()和get y()
- RareSkills
- 发布于 2024-09-28 11:48
- 阅读 1708
这篇文章详细介绍了Curve StableSwap中的get_D()和get_y()函数的数学推导过程,分析了如何通过牛顿法计算流动性池的D值,以及如何在保持平衡的条件下调整代币的值。文章深入探讨了StableSwap的不变量公式,并与实际代码进行了对比,有助于读者理解流动性池的工作原理和算法优化。
这篇文章逐步展示了 get_D() 和 get_y() 的代码是如何从 StableSwap 不变式推导而来的。
给定 StableSwap 不变式:
$$ A \cdot n \sum x_i + D = A \cdot n \cdot D + D^{n+1} \cdot n \prod x_i $$
我们希望对其进行两种常见的数学操作:
- 在 A 和储备 x1,…,xn 的固定值的情况下计算 D。请注意,n,即池支持的代币数量,在池部署时是固定的。这正是函数
get_D()的作用。 - 给定 D,我们希望将一个储备 xi 的值增加到一个新值 xi',并计算另一个储备 xj 需要减少多少,以保持方程的平衡。这正是函数
get_y()的作用。在这里,“y”指的是 xi'。
在 Curve StableSwap 中,这些操作分别称为 get_D() 和 get_y()。
get_D() 的目标
在 Curve V1 (StableSwap) 中,D 类似于 Uniswap V2 中的 k — D 越大,储备就越多,价格曲线的“外推”越远。流动性添加或移除后,或者费用更改池余额后,D 会改变并需要重新计算。这就是函数 get_D() 的用途。给定当前储备的池,它计算 D。
如果一个曲线池持有两个代币 x 和 y,StableSwap 不变式为
$$ 4A(x+y) + D = 4AD + D^{3/4}xy $$
在我们讨论的情况下,“增幅因子” A 可以视为一个常数。
get_y() 的目标
get_y() 函数在交换过程中使用。与 Uniswap V2 中的 k 类似,交换过程中必须保持 D 为常数(忽略费用)。具体来说,给定 x 的新值,它计算出保持方程平衡的 y 的值。因此,它是计算“如果我将这数额的代币 x 放入池中,我可以取出多少代币 y?”的一个重要子程序。
Curve 可以在池中持有超过 2 个代币(例如 3pool 持有 USDT、USDC 和 DAI)。Curve 通过一个数组中的索引来识别这些代币。因此,在这种情况下,x 和 y 指的是该数组中的特定代币。在这个上下文中,get_y() 意味着改变特定代币 x 的余额,同时保持其他余额不变,但允许另一个代币 y 的价值变化。然后,在给定特定的 x 变动后,计算 y 如何变化以保持不变式平衡。
n 个代币的恒等式为:
$$ A \cdot n \sum x_i + D = A \cdot n \cdot D + D^{n+1} \cdot n \prod x_i $$
为简单起见,本文接下来将使用 S 代替求和,使用 P 代替乘积,因此不变式变为:
$$ A \cdot n S + D = A \cdot D^{n} + D^{n+1} \cdot n P $$
其中 S 是代币余额的总和($x_0 + x_1 + … + x_n$),P 是余额的乘积($x_0 x_1 … x_n$),而 $x_i$ 是代币 $i$ 的余额。
在 白皮书 中,S 被写作 $\sum x_i$,而 P 被写作 $\prod x_i$。白皮书中的方程复制如下:
$$ A \cdot n \sum x_i + D = A \cdot D^{n} + D^{n+1} \cdot n \prod x_i $$
我们将使用 S 和 P 来代替求和和乘积符号。
我们假设池可以保存任意数量的 n 个代币,因此公式将反映这一点。然而,实际上,n 必须很小,否则 $D^{n+1}$ 项可能会发生溢出。
使用 get_D() 计算 D
在 get_D() 中,我们得到了一组余额 $x_0, x_1, ..., x_n$,我们要计算 D。
不可能代数求解
$$ A \cdot n S + D = A \cdot D^{n} + D^{n+1} \cdot n P $$
来找出 D。相反,我们需要应用Newton方法来数值解它。为此,我们创建一个函数 f(D),当方程平衡时它等于0。
$$ 0 = A \cdot D^{n} + D^{n+1} \cdot n P - D - A \cdot n S $$
$$ 0 = D^{n+1} \cdot n P + A \cdot D^{n} - D - A \cdot n S $$
$$ f(D) = D^{n+1} \cdot n P + A \cdot n D - D - A \cdot n S $$
然后我们对 D 计算导数 $f'(D)$:
$$ f'(D) = (n+1) D^{n} \cdot n P + A \cdot n - 1 $$
Newton 方法公式
我们可以通过下列公式迭代求解 D:
$$ D_{\text{next}} = D - \frac{f(D)}{f'(D)} $$
将 $f'(D)$ 表示为 D 的分母会比较有用。首先,我们将左侧分数的上下乘以 D。
$$ f'(D) = (n+1) \frac{D^{n+1} \cdot n P}{D} + A \cdot n - 1 $$
然后,将 $f'(D)$ 合并为单个分数:
$$ f'(D) = \frac{(n+1) D^{n+1} \cdot n P + (A \cdot n - 1)D}{D} $$
我们可以重写 Newton 方法,使其具有相同的分母:
$$ D_{\text{next}} = D - \frac{f(D)}{f'(D)} $$ $$ = \frac{D \cdot f'(D)}{f'(D)} - \frac{f(D)}{f'(D)} $$ $$ = \frac{D \cdot f'(D) - f(D)}{f'(D)} $$
通过将前面得到的 $f(D)$ 和 $f'(D)$ 代入重写过的 Newton 方法公式,我们得到:
$$ = \frac{D(n+1)D^{n+1} \cdot n P + (A \cdot n - 1)D - (D^{n+1} \cdot n P + A \cdot n D - D - A \cdot n S)}{(n+1)D^{n+1} \cdot n P + (A \cdot n - 1)D} $$
因为我们重新安排了 $f'(D)$ 以使D 作为分母,所以 $Df'(D)$ 项将很好地相消:
$$ = \frac{(n+1)D^{n+1} \cdot n P + (A \cdot n - 1)D - (D^{n+1} \cdot n P + A \cdot n D - D - A \cdot n S)}{(n+1)D^{n+1} \cdot n P + (A \cdot n - 1)D} $$
$$ = \frac{(n+1)D^{n+1} \cdot n P + (A \cdot n - 1)D - (D^{n+1} \cdot n P + A \cdot n D - D - A \cdot n S)}{(n+1)D^{n+1} \cdot n P + (A \cdot n - 1)D} $$
$$ = \frac{nD^{n+1} \cdot n P + A \cdot n S}{(n+1)D^{n+1} \cdot n P + (A \cdot n - 1)D} $$
我们将分子和分母都乘以 D:
$$ = \frac{(A \cdot n S + nD^{n+1} \cdot n P)D}{(A \cdot n - 1)D + (n+1)D^{n+1} \cdot n P} $$
如果我们定义 $D_P$ 为
$$ D_P = D^{n+1} \cdot n P $$
并替换 $D_P$,我们得到:
$$ D_{\text{next}} = \frac{(A \cdot n S + nD_P) D}{(A \cdot n - 1)D + (n+1)D_P} $$
与原始源代码的比较
这与在 Vyper 代码 中的内容完全匹配:
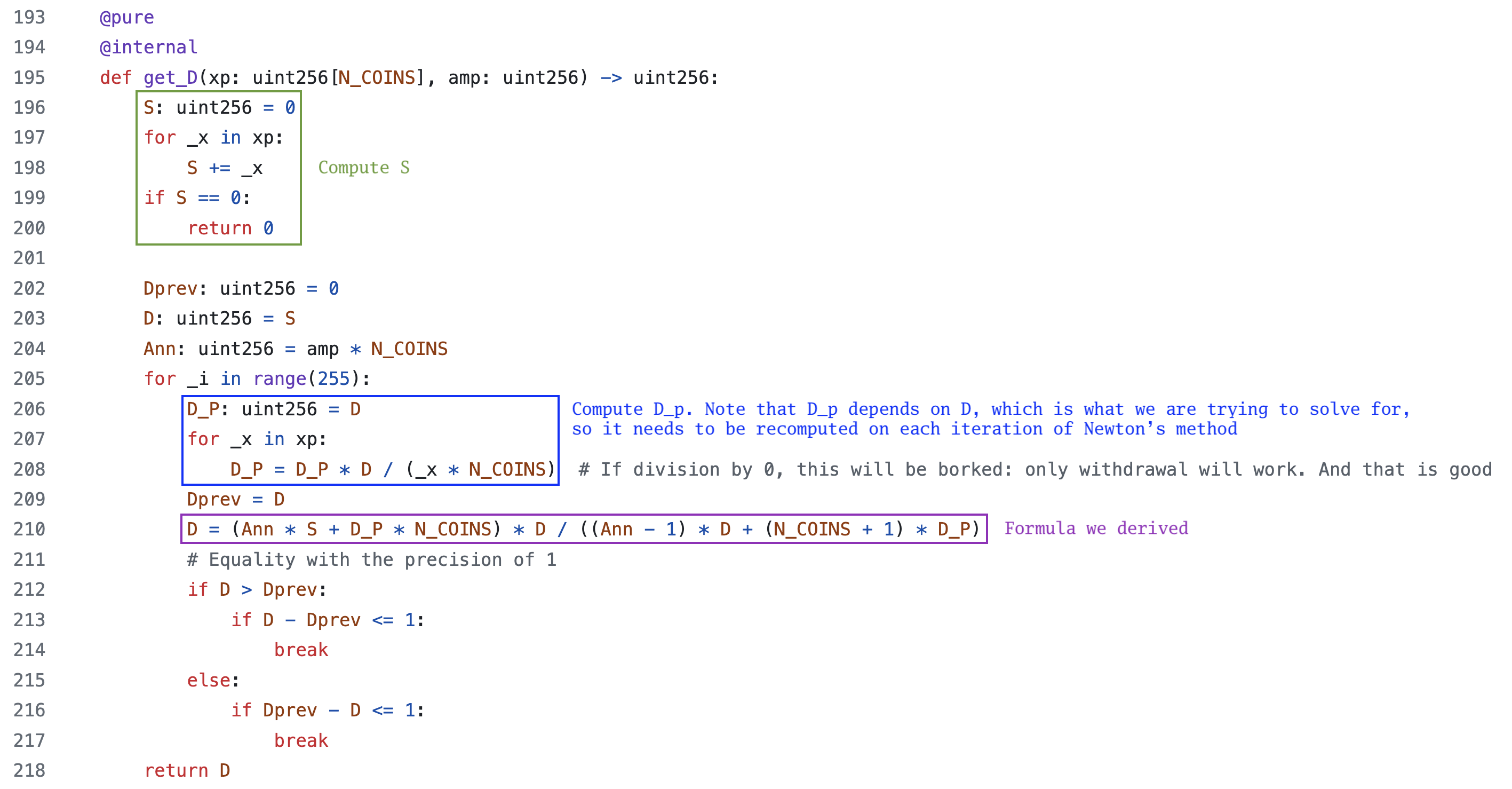
变量 D_P 被定义为:
D_P: uint256 = D # D_P = S
for _x in xp:
D_P = D_P * D / (_x * N_COINS)xp 是代币的数量,因此循环将运行 n 次。因此,我们在分母中得到了 D 自身乘以 n 次。
$$ DP = D^{n+1} \cdot n \prod{i=1}^{n} x_i $$
使用 get_y() 计算 y
这个想法是我们强制其中一个 $x_i$ 采取一个新值(代码称之为 x),并计算出另一个 $x_j$(其中 i≠j)的正确值,使方程保持平衡。其他代币的余额保持不变。$x_j$ 被称为 $y$。
尽管 StableSwap 池可以有多个代币,但一次只能使用 get_y() 交换两个代币。
同样地,我们有相同的不变式:
$$ A \cdot n S + D = A \cdot D^{n} + D^{n+1} \cdot n P $$
D、A 和 n 是固定的,但我们将改变 S 和 P 中的两个值。
$$ S = x_0 + x_1 + … + x_n \ P = x_0 x_1 … x_n $$
因此,我们需要稍微调整公式,因为 S 和 P 包含我们正在计算的值。
- S' 将是所有余额的总和_除了_我们试图求解的代币 $x_i$ 的新余额。
- P 将是所有代币余额的乘积,_除了_我们试图求解的代币。
换句话说:
$$ S = S' + y \ P = P' \cdot y $$
为了与代码保持一致,我们将称我们正在尝试计算其新余额的代币为 $y$。
则公式变为:
$$ A \cdot n (S' + y) + D = A \cdot D^{n} + D^{n+1} \cdot n P' \cdot y $$
同样,我们得出一个 f(y),当方程平衡时它会为0,以及关于 y 的导数:
$$ f(y) = A \cdot D^{n} + D^{n+1} \cdot n P' \cdot y - A \cdot n(S' + y) \ f'(y) = -D^{n+1} \cdot n P' \cdot y^2 - A \cdot n $$
这里再次是 Newton 方法的公式:
$$ y_{\text{next}} = y - \frac{f(y)}{f'(y)} $$
在将 $f(y)$ 和 $f'(y)$ 代入 Newton 方法后,我们得到:
$$ y_{\text{next}} = y - \frac{A \cdot D^{n} + D^{n+1} \cdot n P' \cdot y - A \cdot n(S' + y)}{-D^{n+1} \cdot n P' \cdot y^2 - A \cdot n} $$
把 -1 移到分母外面:
$$ y_{\text{next}} = y - \frac{1}{\left(-A \cdot D^{n} - D^{n+1} \cdot n P' \cdot y + A \cdot n(S' + y)\right)}{D^{n+1} \cdot n P' \cdot y^2 + A \cdot n} $$
再次对 y 乘以分数,使其具有相同的分母:
$$ y_{\text{next}} = y + \frac{A \cdot D^{n} + D^{n+1} \cdot n P' \cdot y - A \cdot n(S' + y)}{D^{n+1} \cdot n P' \cdot y^2 + A \cdot n} $$
$$ y_{\text{next}} = y \cdot \left(D^{n+1} \cdot n P' \cdot y^2 + A \cdot n\right) + (A \cdot D^{n} + D^{n+1} \cdot n P' \cdot y - A \cdot n(S' + y)) - D^{n+1} \cdot n P' \cdot y^2 - A \cdot n $$
将 y 分配到左侧项中:
$$ y_{\text{next}} = y \cdot \left(D^{n+1} \cdot n P' + A \cdot n y + A \cdot D^{n} + D^{n+1} \cdot n P' \cdot y - A \cdot n S' - A \cdot n y - D^{n+1} \cdot n P' \cdot y^2 - A \cdot n\right) $$
结合同分母的总和:
$$ y_{\text{next}} = A \cdot D^{n} + 2D^{n+1} \cdot n P' \cdot y - A \cdot n S' - D^{n+1} \cdot n P' \cdot y^2 - A \cdot n $$
从原始不变式创建一个替代项
看起来方程无法进一步简化,但如果我们重新审视我们的原始不变式:
$$ A \cdot n (S' + y) + D = A \cdot D^{n} + D^{n+1} \cdot n P' \cdot y $$
我们可以求解 $A \cdot D^{n}$,得到:
$$ A \cdot n (S' + y) + D - D^{n+1} \cdot n P' \cdot y = A \cdot D^{n} $$
$$ A \cdot D^{n} = -D^{n+1} \cdot n P' \cdot y + A \cdot n (S' + y) + D $$
然后,如果我们将 $A \cdot D^{n}$ 代入我们计算 $y_{\text{next}}$ 的最新公式的分子中,我们得到:
$$ y_{\text{next}} = A \cdot D^{n} + 2D^{n+1} \cdot n P' \cdot y - A \cdot n S' - D^{n+1} \cdot n P' \cdot y^2 - A \cdot n $$
$$ y_{\text{next}} = \left(-D^{n+1} \cdot n P' \cdot y + A \cdot n (S' + y) + D\right) + 2D^{n+1} \cdot n P' \cdot y - A \cdot n S' - D^{n+1} \cdot n P' \cdot y^2 - A \cdot n $$
许多项发生相消:
$$ y_{\text{next}} = -D^{n+1} \cdot n P' \cdot y + A \cdot n S' + A \cdot n y + D + 2D^{n+1} \cdot n P' \cdot y - A \cdot n S' - D^{n+1} \cdot n P' \cdot y^2 - A \cdot n $$
我们剩下的就是一个更小的方程:
$$ y_{\text{next}} = A \cdot n y + D^{n+1} \cdot n P' \cdot y \cdot \frac{D^{n+1} \cdot n P' \cdot y^2 + A \cdot n}{D^{n+1} \cdot n P'} $$
我们将上下同时乘以 $y^{A \cdot n}$:
$$ y_{\text{next}} = \frac{(A \cdot n y + D^{n+1} \cdot n P')y^{A \cdot n}}{(D^{n+1} \cdot n P' \cdot y^2 + A \cdot n)y^{A \cdot n}} $$
回到我们的不变式,我们可以求解分母中的分数项:
$$ A \cdot n (S' + y) + D = A \cdot D^{n} + D^{n+1} \cdot n P' \cdot y $$
$$ D^{n+1} \cdot n P' \cdot y = A \cdot n (S' + y) + D - A \cdot D^{n} $$
然后我们可以将其代入 $y_{\text{next}}$ 的公式中:
$$ y_{\text{next}} = y^2 + D^{n+1} \cdot n P' \cdot A n \cdot (S' + y) + D - A \cdot D^{n} $$
然后我们可以将 $1/A_n$ 分配并简化分母:
$$ y_{\text{next}} = y^2 + D^{n+1} \cdot n P' \cdot A n (S' + y + D - A)/A_n $$
简化分母,去掉括号并将两个 y 相加:
$$ y_{\text{next}} = y^2 + D^{n+1} \cdot n P' \cdot A n/2y + S' + D/A_n - A $$
在原始代码中,Curve 定义了额外的变量:
$$ c = D^{n+1} \cdot n P' \cdot A n \ b = S' + D/A_n $$
替代到 $y_{\text{next}}$ 的公式中,我们得到:
$$ y_{\text{next}} = y^2 + D^{n+1} \cdot n P' \cdot A n/2y + S' + D/A_n - A $$
与原始源代码的比较
这与 Curve 代码完全匹配,请参阅下方紫色框:

Ann 和 Anⁿ 之间的不匹配
让人困惑的是,Curve 白皮书使用不变式 Ann,但代码库使用的是 Ann。也就是说,代码库似乎在计算 $A \cdot n \cdot n$ 而不是 $A \cdot n^{n}$。这种差异的原因是,代码库将 A 存储为 $A \cdot n - 1$。由于 n 部署时是固定的,预先计算 $n^{n-1}$ 使代码能够避免在链上计算指数,这是一个更昂贵的操作。
总结
Curve 的核心不变式不允许通过符号方法求解变量 D 或 $x_i$。相反,这些项必须通过数值方法来解决。
这次活动的一个启示是,良好的代数操作是一种非常有效的 Gas优化 技术。Curve 开发者能够计算出比直接代入 $f$ 和它的导数相对更小的 Newton 方法公式。
引用与致谢
撰写本文时参考了以下资源:
StableSwap — 稳定币流动性高效机制,Michael Egorov, <https://resources.curve.fi/pdf/curve-stableswap.pdf>
理解 Curve AMM,第一部分:StableSwap 不变式,Atul Agarwal <https://atulagarwal.dev/posts/curveamm/stableswap/>
Curve Finance Discord, “chanho”
<https://discord.com/channels/729808684359876718/729812922649542758/1126630568004698132>
Curve – 代码解析 – get_y() | DeFi, 智能合约程序员 <https://www.youtube.com/watch?v=jAhKbxoeskQ>
- 原文链接: rareskills.io/post/curve...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 保留块及其在不变量验证中的作用 30 浏览
- Certora 中的不变量介绍 24 浏览
- ERC-721 的转移与授权规则 15 浏览
- 约束不变量中的幽灵变量 21 浏览
- 使用Sstore Hook与存储映射 6 浏览
- Solidity智能合约审计2026:定价、AI与预备宣言 372 浏览
- Sudoswap 正在升级 ♨️ 404 浏览
- 第3章:去中心化交易所 2629 浏览
- 慢雾:去中心化永续合约安全审计指南 1100 浏览
- 流动性池有了代理:KOPS如何解决凌晨2点的再平衡问题 814 浏览
- Balancer稳定币交换分析与差分模糊测试指南 910 浏览
- AMM 安全深度解析 - 第2部分:主流 DEX 平台深度解析 4349 浏览

