掌握椭圆曲线算术 - 带有 SageMath 示例的综合指南

thogiti
发布于 2023-10-19 18:24
阅读 45

这篇文章详细介绍了椭圆曲线及其在现代加密中的应用，尤其是椭圆曲线密码学（ECC）。文章涵盖了椭圆曲线的基本概念、算术运算、在SageMath中的实现以及ECC在通信安全、数字签名和密钥交换中的应用。通过丰富的代码示例和可视化图表，读者可以深入理解椭圆曲线加密的理论基础和实践应用。

- [介绍：揭开椭圆曲线及其应用的神秘面纱](#介绍：揭开椭圆曲线及其应用的神秘面纱)
  - [椭圆曲线密码学（ECC）的力量](#椭圆曲线密码学-ecc-的力量)
  - [利用 SageMath 打开 ECC 的潜力](#利用-sagemath-打开-ecc-的潜力)
- [理解椭圆曲线的基础知识](#理解椭圆曲线的基础知识)
  - [椭圆曲线的定义](#椭圆曲线的定义)
  - [椭圆曲线上的点](#椭圆曲线上的点)
  - [可视化椭圆曲线上的点](#可视化椭圆曲线上的点)
  - [探索椭圆曲线群的结构](#探索椭圆曲线群的结构)
- [椭圆曲线算术](#椭圆曲线算术)
  - [在椭圆曲线上进行点加法](#在椭圆曲线上进行点加法)
  - [掌握点翻倍技巧](#掌握点翻倍技巧)
  - [高效的标量乘法算法](#高效的标量乘法算法)
  - [计算点的逆](#计算点的逆)
  - [验证椭圆曲线算术中的结合律和交换律](#验证椭圆曲线算术中的结合律和交换律)
  - [可视化椭圆曲线算术操作](#可视化椭圆曲线算术操作)
- [在 SageMath 中使用椭圆曲线](#在-sagemath-中使用椭圆曲线)
  - [使用 SageMath 定义和可视化椭圆曲线](#使用-sagemath-定义和可视化椭圆曲线)
  - [发现椭圆曲线上的点](#发现椭圆曲线上的点)
  - [在 SageMath 中操作椭圆曲线群](#在-sagemath-中操作椭圆曲线群)
    - [点加法](#点加法)
    - [点翻倍](#点翻倍)
    - [标量乘法](#标量乘法)
    - [多标量乘法](#多标量乘法)
- [椭圆曲线算术的应用](#椭圆曲线算术的应用)
  - [利用椭圆曲线密码学 (ECC) 确保通信安全](#利用椭圆曲线密码学-ecc-确保通信安全)
  - [利用数字签名 (ECDSA) 确保数据完整性](#利用数字签名-ecdsa-确保数据完整性)
  - [利用密钥交换 (ECDH) 建立安全连接](#利用密钥交换-ecdh-建立安全连接)
  - [以太坊区块链应用](#以太坊区块链应用)
  - [使用 Plonk 的零知识投票](#使用-plonk-的零知识投票)
- [反思椭圆曲线算术的力量](#反思椭圆曲线算术的力量)
  - [通过高级 ECC 主题扩展你的知识](#通过高级-ecc-主题扩展你的知识)
  - [探索更多资源和学习材料](#探索更多资源和学习材料)

## 介绍：揭开椭圆曲线及其应用的神秘面纱

椭圆曲线是数学中的一个迷人领域，在现代密码学中得到广泛应用，特别是在椭圆曲线密码学（ECC）领域。ECC 的受欢迎程度源于其能够提供与传统密码学方法（如 RSA）相同级别的安全性，但所需的密钥尺寸更小。这导致更快的计算速度和减少的存储需求，使得 ECC 成为在资源受限环境中保护通信的一个吸引人的选择。

在这篇博客中，我们旨在提供对椭圆曲线算术及其在密码学中应用的全面介绍。我们将探讨椭圆曲线的基本概念，深入了解对其进行的算术操作，并演示如何使用强大的 SageMath 软件与椭圆曲线进行操作。到这篇文章结束时，你将对椭圆曲线算术的基础有一个扎实的理解，并能够探索更高级的 ECC 主题。

### 椭圆曲线密码学（ECC）的力量

ECC 是一种公钥密码系统，依赖于有限域上的椭圆曲线的代数结构。它相较于传统密码系统有几个优点，如：

1. **更小的密钥尺寸**：ECC 提供与 RSA 相同的安全级别，但密钥尺寸显著更小。例如，256 位的 ECC 密钥被认为与 3072 位的 RSA 密钥同样安全。

2. **更快的计算速度**：由于密钥尺寸较小，ECC 操作通常比其 RSA 对应操作快，使得 ECC 更适合资源受限的设备。

3. **增强的安全性**：ECC 被认为在某些类型的攻击，如量子计算攻击方面具有更好的抗性，相较于传统密码系统来说。这使得 ECC 成为在面对不断变化的威胁时保护通信的前瞻性选择。

### 利用 SageMath 打开 ECC 的潜力

SageMath [sagemath.org](https://www.sagemath.org/) 是一个开源数学软件系统，提供了一个强大的环境，用于处理各种数学结构，包括椭圆曲线。它提供了一套丰富的工具和库，用于在椭圆曲线上执行算术操作，使其成为学习和实验 ECC 的理想平台。

![椭圆曲线示例](https://upload.wikimedia.org/wikipedia/commons/thumb/2/2b/Elliptic_curve_simple.svg/2560px-Elliptic_curve_simple.svg.png)

在这篇博客中，我们将涵盖以下主题：

- 椭圆曲线基础：定义、点和示例图
- 椭圆曲线算术：点加法、翻倍、标量乘法和计算点的逆
- 在 SageMath 中使用椭圆曲线：定义、绘图和寻找曲线上的点
- 在 SageMath 中实现椭圆曲线算术：点加法、翻倍、标量乘法和计算点的逆的代码示例
- 椭圆曲线算术的应用：保护通信（ECC）、数字签名（ECDSA）和密钥交换（ECDH）、区块链协议、零知识证明（ZKP）、零知识机器学习

到这篇文章结束时，你将拥有对椭圆曲线算术的扎实基础，并为探索更高级的 ECC 主题及其在密码学中的应用做好充分准备。

## 理解椭圆曲线的基础知识

椭圆曲线是现代密码学中发挥重要作用的代数结构。为了理解椭圆曲线的基础知识，让我们从其定义开始。

### 椭圆曲线的定义

椭圆曲线由以下形式的方程定义：

$$y^2 = x^3 + ax + b$$

其中 $a$ 和 $b$ 是常数，并且曲线必须满足条件 $4a^3 + 27b^2 \neq 0$ 以确保它没有奇点（即没有自交或尖点）。在密码学的背景下，我们通常在有限域上使用椭圆曲线，这意味着坐标 $(x, y)$ 和常数 $a$ 和 $b$ 是有限域的元素。

### 椭圆曲线上的点

椭圆曲线上的点 $(x, y)$ 满足曲线的方程。除了位于曲线上的点外，还有一个额外的“无穷远点”用 $\mathcal{O}$ 表示，作为椭圆曲线群的恒等元素（稍后会详细讨论）。

### 可视化椭圆曲线上的点

为了可视化椭圆曲线，我们可以绘制满足曲线方程的点。让我们使用 SageMath 绘制一个椭圆曲线的示例。

```python
a, b = -1, 1
E = EllipticCurve([a, b])
plot(E, xmin=-3, xmax=3, ymin=-3, ymax=3)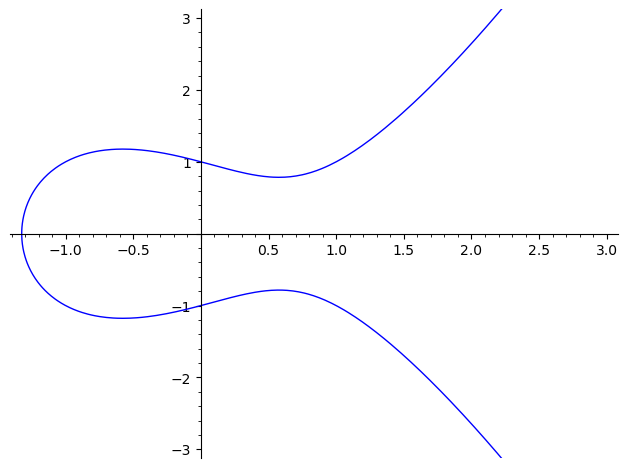
```

![椭圆曲线图](https://img.learnblockchain.cn/2025/03/29/sagemath-elliptic-curve-example.png)

*使用 SageMath 生成的椭圆曲线图的示例。*

### 探索椭圆曲线群的结构

椭圆曲线具有内在的群结构，这是椭圆曲线算术的基础。群运算定义为曲线上点的加法。无穷远点 $\mathcal{O}$ 作为恒等元素，这意味着对曲线上任何一点 $P$，都有 $P + \mathcal{O} = P$。

群运算具有以下属性：

1. **封闭性**：任意两个曲线上的点的和也是曲线上的一个点。
2. **结合性**：对曲线上的任意点 $P$、$Q$ 和 $R$ ，有 $(P + Q) + R = P + (Q + R)$。
3. **恒等**：存在恒等元素 $\mathcal{O}$，对于曲线上任何一点 $P$，有 $P + \mathcal{O} = P$。
4. **逆元**：对曲线上的任何一点 $P$，存在逆点 $-P$，使得 $P + (-P) = \mathcal{O}$。

椭圆曲线的群结构使我们能够在点上执行算术运算，这是椭圆曲线密码学的基础。

在接下来的部分中，我们将深入探讨椭圆曲线算术，并展示如何使用 SageMath 与椭圆曲线进行操作。通过理解椭圆曲线的基础知识及其群结构，你将准备好探索椭圆曲线密码学及其应用中的更高级主题。

## 椭圆曲线算术

椭圆曲线算术是椭圆曲线密码学的基础。在这一部分，我们将涵盖以下主题：

- 在椭圆曲线上进行点加法
- 掌握点翻倍技巧
- 高效的标量乘法算法
- 计算点的逆
- 验证椭圆曲线算术中的结合律和交换律

### 在椭圆曲线上进行点加法

点加法是椭圆曲线算术中的主要运算。给定曲线上的两个点 $P$ 和 $Q$，它们的和 $R = P + Q$ 的计算步骤如下：

1. 找到经过 $P$ 和 $Q$ 的直线 $L$。
2. 找到直线 $L$ 与椭圆曲线的第三个交点 $R'$。
3. 将 $R'$ 反射到 x 轴以获得 $R$。

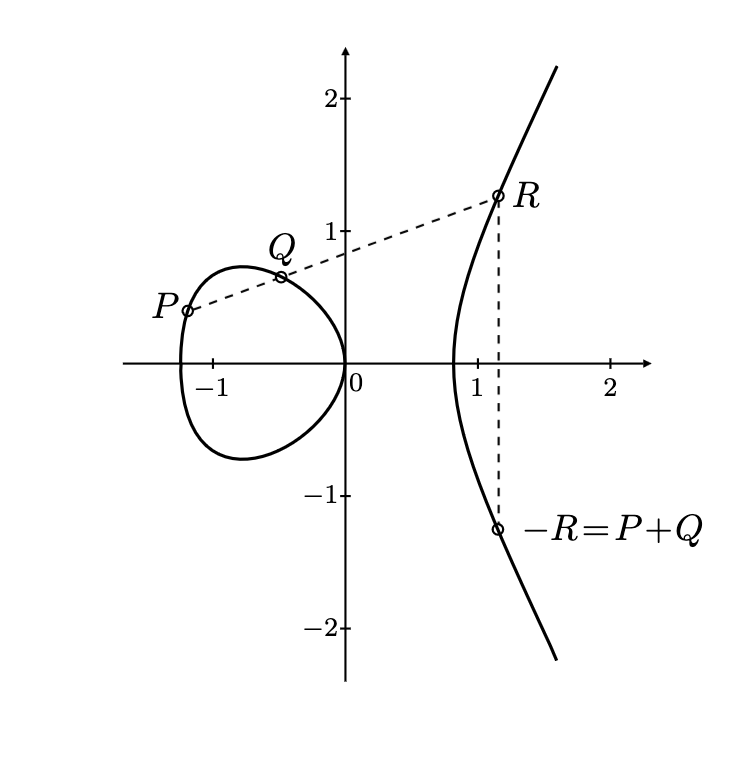
![椭圆曲线上的点加法](https://img.learnblockchain.cn/2025/03/29/point-addition-in-ECC.png)

*椭圆曲线上点加法的几何可视化。*

在 SageMath 中，可以使用 `+` 操作符进行点加法：

```python
p = 2^256 - 2^32 - 977
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])
P = E.random_element()
Q = E.random_element()
R = P + Q
print(" P+Q = ", R)
```

### 掌握点翻倍技巧

点翻倍是点加法的特例，其中 $P = Q$。在这种情况下，直线 $L$ 是点 $P$ 处的切线。计算 $R = 2P$ 的过程与点加法类似：

1. 找到点 $P$ 的切线 $L$。
2. 找到直线 $L$ 与椭圆曲线的第二个交点 $R'$。
3. 将 $R'$ 反射到 x 轴以获得 $R$。

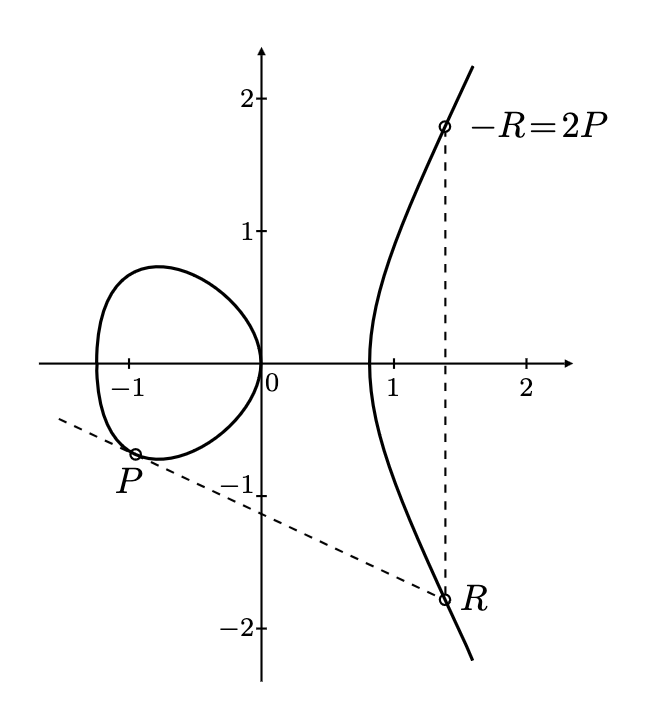
![椭圆曲线上的点翻倍](https://img.learnblockchain.cn/2025/03/29/point-doubling-in-ECC.png)

*椭圆曲线上点翻倍的几何可视化。*

在 SageMath 中，点翻倍可以使用 `*` 操作符进行：

```python
p = 2^256 - 2^32 - 977
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])
P = E.random_element()
R = 2 * P
print(" 2*P = ", R)
```

### 高效的标量乘法算法

标量乘法是将点 $P$ 自己加上 $k$ 次的操作，记作 $[k]P$。如双倍加法算法等高效的标量乘法算法可以显著提高椭圆曲线密码学的性能。

在 SageMath 中，标量乘法可以使用 `*` 操作符执行：

```python
p = 2^256 - 2^32 - 977
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])
P = E.random_element()
k = randint(1, E.order() - 1)
R = k * P
print(" k*P = ", R)
```

### 计算点的逆

椭圆曲线上点 $P = (x, y)$ 的逆点为 $-P = (x, -y)$。逆点用于椭圆曲线算术中计算两个点之间的差。

在 SageMath 中，可以使用 `neg` 方法计算点的逆：

```python
p = 2^256 - 2^32 - 977
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])
P = E.random_element()
P_inv = -P
print(" P_inv = ", P_inv)
```

### 验证椭圆曲线算术中的结合律和交换律

结合律和交换律是椭圆曲线算术的重要性质。我们可以执行算术运算在随机点上并检查结果是否满足这些性质。

在 SageMath 中，我们可以这样验证结合律和交换律：

```python
P = E.random_element()
Q = E.random_element()
R = E.random_element()

## 验证结合律: (P + Q) + R == P + (Q + R)
print((P + Q) + R == P + (Q + R))

## 验证交换律: P + Q == Q + P
print(P + Q == Q + P)
```

通过理解椭圆曲线算术的基础知识，以及掌握点加法、点翻倍、标量乘法和计算点的逆的技巧，你将为探索椭圆曲线密码学和其应用中的更高级主题做好充分准备。

### 可视化椭圆曲线算术操作

为了更好地理解椭圆曲线上的算术操作，我们可以通过图形可视化点加法、点翻倍和标量乘法的过程。

在 SageMath 中，我们可以绘制椭圆曲线和参与算术操作的点：

```python
p = 13
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])

def plot_points_on_curve(E, points, labels, colors):
    curve_plot = plot(E, xmin=-5, xmax=5, ymin=-5, ymax=5)
    real_points = [(float(pt[0]), float(pt[1])) for pt in points]
    point_plots = [point2d(pt, color=colors[i], size=30, zorder=5) + text(labels[i], pt, fontsize=10, color=colors[i], horizontal_alignment='left', vertical_alignment='bottom') for i, pt in enumerate(real_points)]
    return curve_plot + sum(point_plots)

P = E.random_element()
Q = E.random_element()
R = P + Q

plot_points_on_curve(E, [P.xy(), Q.xy(), R.xy()], ['P', 'Q', 'R'], ['red', 'blue', 'green'])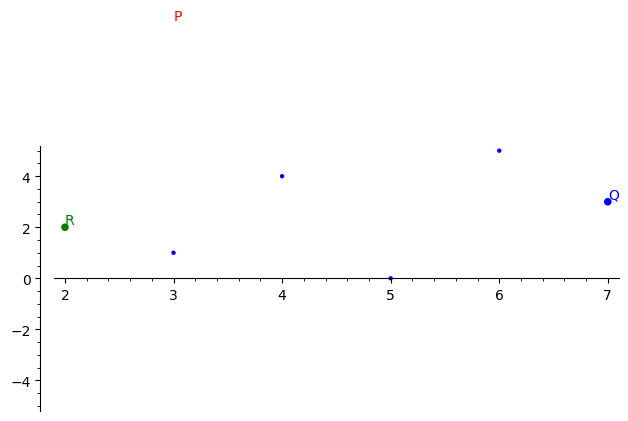
```

![椭圆曲线算术可视化](https://img.learnblockchain.cn/2025/03/29/point-addition-ecc-visualiation.png)

*使用 SageMath 生成的包含点 P、Q 和 R 的椭圆曲线图的示例。*

通过可视化椭圆曲线上的算术操作，我们可以更深入理解潜在的数学概念及其在密码学中的应用。

我们已经涵盖了椭圆曲线算术的基础，包括点加法、点翻倍、标量乘法、计算点的逆以及验证结合律和交换律。我们还演示了如何使用 SageMath 执行这些操作，并可视化结果以提升理解。

通过掌握这些概念和技巧，你将为探索椭圆曲线密码学中的更高级主题（如密钥交换、数字签名和安全通信协议）做好充分准备。

## 在 SageMath 中使用椭圆曲线

SageMath 是一个强大的开源数学软件系统，提供了大量支持用于操作椭圆曲线的功能。在这一部分，我们将覆盖以下主题：

- 使用 SageMath 定义和可视化椭圆曲线
- 发现椭圆曲线上的点
- 在 SageMath 中操作椭圆曲线群

### 使用 SageMath 定义和可视化椭圆曲线

要在 SageMath 中定义椭圆曲线，我们可以使用 `EllipticCurve` 函数，该函数接受一个系数列表 `[a, b]`，对应于曲线方程 $y^2 = x^3 + ax + b$：

```python
a, b = -1, 1
E = EllipticCurve([a, b])
```

为了可视化椭圆曲线，我们可以使用 `plot` 函数：

```python
plot(E, xmin=-5, xmax=5, ymin=-5, ymax=5)
```

![椭圆曲线图](https://img.learnblockchain.cn/2025/03/29/sagemath-elliptic-curve-example.png)

*使用 SageMath 生成的椭圆曲线图的示例。*

### 发现椭圆曲线上的点

要找到椭圆曲线上的点，我们可以使用 `points` 方法，该方法返回有限域内曲线上的点列表：

```python
p = 13
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])
points = E.points()
print(points)
```

输出：

```
[(0 : 1 : 0), (7 : 5 : 1), (7 : 8 : 1), (8 : 5 : 1), (8 : 8 : 1), (11 : 5 : 1), (11 : 8 : 1)]
```

### 在 SageMath 中操作椭圆曲线群

椭圆曲线具有内在的群结构，使我们能够在点之间执行算术运算。SageMath 提供了多种方法来操纵椭圆曲线群，例如点加法、点翻倍和标量乘法。

#### 点加法

要在椭圆曲线上添加两个点，我们可以使用 `+` 操作符：

```python
P = E.random_element()
Q = E.random_element()
R = P + Q
```

#### 点翻倍

要在椭圆曲线上双倍一个点，我们可以使用 `*` 操作符：

```python
P = E.random_element()
R = 2 * P
```

#### 标量乘法

要对一个点执行标量乘法，我们可以使用 `*` 操作符：

```python
P = E.random_point()
k = randint(1, E.order() - 1)
R = k * P
```

#### 多标量乘法

多标量乘法是计算给定标量系数的椭圆曲线上点的线性组合的操作。给定点 $P_1, P_2, \dots, P_n$ 和标量 $k_1, k_2, \dots, k_n$，多标量乘法计算结果 $R = k_1P_1 + k_2P_2 + \dots + k_nP_n$。高效的多标量乘法算法，如 Pippenger 算法或交错窗口法，可以显著提升椭圆曲线密码学的性能。

在 SageMath 中，我们可以使用循环与 `+` 和 `*` 操作符执行多标量乘法：

```python
points = [E.random_element() for _ in range(5)]
scalars = [randint(1, E.order() - 1) for _ in range(5)]

R = E(0)  # 将 R 初始化为椭圆曲线群的恒等元素
for i in range(len(points)):
    R += scalars[i] * points[i]
print(" 多标量乘法: ", R)
```

或者，我们可以使用 `sum` 函数和列表推导来实现相同的结果：

```python
R = sum(scalars[i] * points[i] for i in range(len(points)))
print(" 多标量乘法: ", R)
```

通过理解多标量乘法及其高效算法，你可以进一步优化椭圆曲线操作，从而增强基于椭圆曲线的密码协议的性能。

在椭圆曲线密码学中，有几种有效的多标量乘法计算（MSM）算法。五种流行的算法是：

1. 双倍加法算法：这是最基本的标量乘法算法，类似于模幂运算中的平方-乘法算法。它通过迭代 $k$ 的比特，对当前点在每个步骤进行翻倍，并在 $k$ 中的相应位为 1 时添加 $P$ 来计算 $kP$ [en.wikipedia.org](https://en.wikipedia.org/wiki/Elliptic_curve_point_multiplication)。

2. Montgomery 梯子：该算法使用梯形结构计算标量乘法，既高效又抵抗旁路攻击。它仅对 x 坐标操作，非常适合以 Montgomery 形式呈现的曲线 [en.wikipedia.org](https://en.wikipedia.org/wiki/Elliptic_curve_point_multiplication)。

3. wNAF（窗口非相邻形式）方法：该算法利用窗口非相邻形式，这是标量的带符号二进制表示。通过减少所需的点加法数量，它可以更快地进行计算 [en.wikipedia.org](https://en.wikipedia.org/wiki/Elliptic_curve_point_multiplication)。

4. Straus 算法（也称为 Shamir 技巧）：该算法比分别执行两个标量乘法更有效地计算多标量乘法（$kP + lQ$）。它将双倍加法算法与交错结合，允许同时计算 $kP$ 和 $lQ$ [eprint.iacr.org](https://eprint.iacr.org/2003/257.pdf)。

5. Pippenger 算法：该算法是 Straus 算法的推广，用于计算两个以上点的多标量乘法。它将标量分成更小的组，并分别计算每个组的标量乘法，然后合并结果 [cr.yp.to](https://cr.yp.to/papers/pippenger.pdf)。

我们已经探索了如何在 SageMath 中使用椭圆曲线，包括定义和可视化椭圆曲线，发现椭圆曲线上的点，以及操作椭圆曲线群。通过理解这些概念和技巧，你将为探索椭圆曲线密码学和其应用领域中的更高级主题做好充分准备。

SageMath 为操作椭圆曲线提供了一个强大且用户友好的环境，使其成为研究人员、学生和密码学领域从业人员的重要工具。通过掌握使用 SageMath 进行椭圆曲线操作，你将能够高效地实现和分析基于椭圆曲线的密码算法，为数字世界的安全和高效通信铺平道路。

## 椭圆曲线算术的应用

椭圆曲线算术在各种密码学应用中发挥着重要作用，包括保护通信、确保数据完整性、建立安全连接以及实现隐私保护协议。在这一部分中，我们将讨论椭圆曲线算术的以下应用：

- 椭圆曲线密码学（ECC）
- 数字签名（ECDSA）
- 密钥交换（ECDH）
- 以太坊区块链应用
- 使用 Plonk 的零知识投票

### 利用椭圆曲线密码学 (ECC) 确保通信安全

椭圆曲线密码学（ECC）是一种基于有限域上椭圆曲线的公钥密码系统。ECC 提供与传统密码系统如 RSA 相同的安全级别，但密钥尺寸更小，使其更高效，适合资源受限的环境。

```python
## 生成一个椭圆曲线和一个基点
E = EllipticCurve(GF(2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1), [0, 7])
G = E.random_point()

## 为 Alice 生成一个私钥-公钥对
a = randint(1, E.order() - 1)
A = a * G

## 为 Bob 生成一个私钥-公钥对
b = randint(1, E.order() - 1)
B = b * G

## Alice 和 Bob 计算共享密钥
shared_secret_A = a * B
shared_secret_B = b * A
print("共享密钥 A == 共享密钥 B? ", shared_secret_A == shared_secret_B)

```

### 利用数字签名 (ECDSA) 确保数据完整性

椭圆曲线数字签名算法（ECDSA）是一种广泛使用的数字签名方案，提供数据完整性和身份验证。ECDSA 签名比 RSA 签名更小且计算更快，因此适用于各种应用。

```python
from hashlib import sha256

E = EllipticCurve(GF(2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1), [0, 7])
G = E.random_point()

## 为签名者生成私钥-公钥对
d = randint(1, E.order() - 1)
Q = d * G

## 签署消息
message = b"Hello, world!"
hash_value = int.from_bytes(sha256(message).digest(), 'big')
k = randint(1, E.order() - 1)
R = k * G
r = Integer(R[0]) % E.order()  # 在进行模运算前先将 R[0] 转换为整数
s = ((hash_value + d * r) * inverse_mod(k, E.order())) % E.order()

## 验证签名
w = inverse_mod(s, E.order())
u1 = (hash_value * w) % E.order()
u2 = (r * w) % E.order()
X = u1 * G + u2 * Q
print("签名是否相同? ", r % E.order() == Integer(X[0]) % E.order())  # 在进行模运算前将 X[0] 转换为整数

```

### 利用密钥交换 (ECDH) 建立安全连接

椭圆曲线 Diffie-Hellman（ECDH）密钥交换协议使两方能够通过不安全的通道建立共享密钥。ECDH 提供与传统的 Diffie-Hellman 相同级别的安全性，但具有更小的密钥尺寸和更快的计算速度。

```python
## 定义椭圆曲线
E = EllipticCurve(GF(2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1), [0, 7])
G = E.random_point()

## 为 Alice 生成一个私钥-公钥对
a = randint(1, E.order() - 1)
A = a * G

## 为 Bob 生成一个私钥-公钥对
b = randint(1, E.order() - 1)
B = b * G

## Alice 和 Bob 计算共享密钥
shared_secret_A = a * B
shared_secret_B = b * A
print(" shared_secret_A == shared_secret_B? ", shared_secret_A == shared_secret_B)

```

### 以太坊区块链应用

椭圆曲线算术在以太坊区块链应用中得到广泛使用，例如智能合约和零知识证明。以太坊使用 secp256k1 椭圆曲线进行其加密操作，包括生成地址和签署交易。

```python
from hashlib import sha256

## 定义 secp256k1 椭圆曲线
p = 2^256 - 2^32 - 977
E = EllipticCurve(GF(p), [0, 7])
G = E.lift_x(55066263022277343669578718895168534326250603453777594175500187360389116729240)

## 为以太坊用户生成私钥-公钥对
private_key = randint(1, E.order() - 1)
public_key = private_key * G

## 以太坊地址生成（简化版）
address = sha256(str(public_key).encode()).hexdigest()[-40:]
print("以太坊地址:", "0x"+address)

```

### 使用 Plonk 的零知识投票

Plonk 是一种高效的零知识证明系统，利用椭圆曲线算术来实现隐私保护协议，如零知识投票。Plonk 使用基于椭圆曲线的 Kate-Zaverucha-Goldberg（KZG）多项式承诺方案。

```python
## 定义椭圆曲线和 Plonk 的基点
p = 2^256 - 2^32 - 977
E = EllipticCurve(GF(p), [0, 7])
G = E.lift_x(55066263022277343669578718895168534326250603453777594175500187360389116729240)

## 生成一个多项式的 KZG 承诺
def kzg_commit(poly_coeffs, G):
    return sum(coeff * (G * i) for i, coeff in enumerate(poly_coeffs))

## 示例多项式及其承诺
poly_coeffs = [1, 2, 3, 4]
C = kzg_commit(poly_coeffs, G)
print(C)

```

在使用 Plonk 的零知识投票系统中，投票者可以证明他们的投票有效，而无需透露其实际选择。这确保了投票过程的隐私和完整性。

总结来说，椭圆曲线算术是多种密码学应用的重要基础，包括保护通信、确保数据完整性、建立安全连接以及实现隐私保护协议。通过使用 SageMath 理解和实现这些应用，你可以利用椭圆曲线密码学的力量来开发安全且高效的解决方案，以应对现实世界中的问题。

## 反思椭圆曲线算术的力量

椭圆曲线算术在现代密码学中被证明是一种强大的工具，为各种应用提供了高效和安全的解决方案。其较小的密钥尺寸和更快的计算使其成为适用于资源受限环境和隐私保护协议的吸引人选择。

### 通过高级 ECC 主题扩展你的知识

为了进一步增强你对椭圆曲线密码学的理解，可以考虑探索以下高级主题：

- 基于配对的密码学：利用椭圆曲线上的双线性配对来实现新颖的密码学原语，如基于身份的加密（IBE）和基于属性的加密（ABE）。
- 基于格的密码学：研究椭圆曲线密码学与基于格的密码学之间的联系，后者被认为能够抵抗量子攻击。
- 同态基于椭圆曲线的密码学：研究椭圆曲线之间的同态映射，这可以用于构建后量子密码方案。

### 探索更多资源和学习材料

为了深入了解椭圆曲线算术及其应用，可以参考以下资源：

- 书籍：
  - J.S. Milne 的《A Course in Elliptic Curves》
  - Lawrence C. Washington 的《Elliptic Curves: Number Theory and Cryptography》
- 在线课程：
  - [斯坦福大学的密码学课程](https://www.coursera.org/course/crypto) 
  - [麻省理工学院的计算机科学数学课程](https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-042j-mathematics-for-computer-science-fall-2005/)
- 研究论文：
  - [椭圆曲线密码学：温和的介绍](https://learnblockchain.cn/article/8731)
  - [椭圆曲线密码学概述](https://eprint.iacr.org/2018/825.pdf)

通过扩展你在椭圆曲线算术方面的知识，并探索高级主题，你可以保持在密码学的前沿并为开发安全高效的现实问题解决方案做出贡献。

你可以在 GitHub 仓库 [github.com/thogiti](https://github.com/thogiti/Elliptic-curve-arithmetic-sage) 找到完整的 SageMath 代码。

>- 原文链接： [github.com/thogiti/thogi...](https://github.com/thogiti/thogiti.github.io/blob/master/_posts/2023-05-09-Mastering-Elliptic-Curve-Arithmetic-A-Comprehensive-Guide-with-SageMath-Examples.md)
>- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～

介绍：揭开椭圆曲线及其应用的神秘面纱
- 椭圆曲线密码学（ECC）的力量
- 利用 SageMath 打开 ECC 的潜力
理解椭圆曲线的基础知识
椭圆曲线算术
在 SageMath 中使用椭圆曲线
椭圆曲线算术的应用
反思椭圆曲线算术的力量
- 通过高级 ECC 主题扩展你的知识
- 探索更多资源和学习材料

介绍：揭开椭圆曲线及其应用的神秘面纱

椭圆曲线密码学（ECC）的力量

ECC 是一种公钥密码系统，依赖于有限域上的椭圆曲线的代数结构。它相较于传统密码系统有几个优点，如：

更小的密钥尺寸：ECC 提供与 RSA 相同的安全级别，但密钥尺寸显著更小。例如，256 位的 ECC 密钥被认为与 3072 位的 RSA 密钥同样安全。
更快的计算速度：由于密钥尺寸较小，ECC 操作通常比其 RSA 对应操作快，使得 ECC 更适合资源受限的设备。
增强的安全性：ECC 被认为在某些类型的攻击，如量子计算攻击方面具有更好的抗性，相较于传统密码系统来说。这使得 ECC 成为在面对不断变化的威胁时保护通信的前瞻性选择。

利用 SageMath 打开 ECC 的潜力

SageMath sagemath.org 是一个开源数学软件系统，提供了一个强大的环境，用于处理各种数学结构，包括椭圆曲线。它提供了一套丰富的工具和库，用于在椭圆曲线上执行算术操作，使其成为学习和实验 ECC 的理想平台。

在这篇博客中，我们将涵盖以下主题：

椭圆曲线基础：定义、点和示例图
椭圆曲线算术：点加法、翻倍、标量乘法和计算点的逆
在 SageMath 中使用椭圆曲线：定义、绘图和寻找曲线上的点
在 SageMath 中实现椭圆曲线算术：点加法、翻倍、标量乘法和计算点的逆的代码示例
椭圆曲线算术的应用：保护通信（ECC）、数字签名（ECDSA）和密钥交换（ECDH）、区块链协议、零知识证明（ZKP）、零知识机器学习

到这篇文章结束时，你将拥有对椭圆曲线算术的扎实基础，并为探索更高级的 ECC 主题及其在密码学中的应用做好充分准备。

理解椭圆曲线的基础知识

椭圆曲线是现代密码学中发挥重要作用的代数结构。为了理解椭圆曲线的基础知识，让我们从其定义开始。

椭圆曲线的定义

椭圆曲线由以下形式的方程定义：

$$y^2 = x^3 + ax + b$$

椭圆曲线上的点

可视化椭圆曲线上的点

为了可视化椭圆曲线，我们可以绘制满足曲线方程的点。让我们使用 SageMath 绘制一个椭圆曲线的示例。

a, b = -1, 1
E = EllipticCurve([a, b])
plot(E, xmin=-3, xmax=3, ymin=-3, ymax=3)

使用 SageMath 生成的椭圆曲线图的示例。

探索椭圆曲线群的结构

群运算具有以下属性：

封闭性：任意两个曲线上的点的和也是曲线上的一个点。
结合性：对曲线上的任意点 $P$、$Q$ 和 $R$ ，有 $(P + Q) + R = P + (Q + R)$。
恒等：存在恒等元素 $\mathcal{O}$，对于曲线上任何一点 $P$，有 $P + \mathcal{O} = P$。
逆元：对曲线上的任何一点 $P$，存在逆点 $-P$，使得 $P + (-P) = \mathcal{O}$。

椭圆曲线的群结构使我们能够在点上执行算术运算，这是椭圆曲线密码学的基础。

椭圆曲线算术

椭圆曲线算术是椭圆曲线密码学的基础。在这一部分，我们将涵盖以下主题：

在椭圆曲线上进行点加法
掌握点翻倍技巧
高效的标量乘法算法
计算点的逆
验证椭圆曲线算术中的结合律和交换律

在椭圆曲线上进行点加法

点加法是椭圆曲线算术中的主要运算。给定曲线上的两个点 $P$ 和 $Q$，它们的和 $R = P + Q$ 的计算步骤如下：

找到经过 $P$ 和 $Q$ 的直线 $L$。
找到直线 $L$ 与椭圆曲线的第三个交点 $R'$。
将 $R'$ 反射到 x 轴以获得 $R$。

椭圆曲线上点加法的几何可视化。

在 SageMath 中，可以使用 + 操作符进行点加法：

p = 2^256 - 2^32 - 977
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])
P = E.random_element()
Q = E.random_element()
R = P + Q
print(" P+Q = ", R)

掌握点翻倍技巧

点翻倍是点加法的特例，其中 $P = Q$。在这种情况下，直线 $L$ 是点 $P$ 处的切线。计算 $R = 2P$ 的过程与点加法类似：

找到点 $P$ 的切线 $L$。
找到直线 $L$ 与椭圆曲线的第二个交点 $R'$。
将 $R'$ 反射到 x 轴以获得 $R$。

椭圆曲线上点翻倍的几何可视化。

在 SageMath 中，点翻倍可以使用 * 操作符进行：

p = 2^256 - 2^32 - 977
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])
P = E.random_element()
R = 2 * P
print(" 2*P = ", R)

高效的标量乘法算法

标量乘法是将点 $P$ 自己加上 $k$ 次的操作，记作 $[k]P$。如双倍加法算法等高效的标量乘法算法可以显著提高椭圆曲线密码学的性能。

在 SageMath 中，标量乘法可以使用 * 操作符执行：

p = 2^256 - 2^32 - 977
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])
P = E.random_element()
k = randint(1, E.order() - 1)
R = k * P
print(" k*P = ", R)

计算点的逆

椭圆曲线上点 $P = (x, y)$ 的逆点为 $-P = (x, -y)$。逆点用于椭圆曲线算术中计算两个点之间的差。

在 SageMath 中，可以使用 neg 方法计算点的逆：

p = 2^256 - 2^32 - 977
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])
P = E.random_element()
P_inv = -P
print(" P_inv = ", P_inv)

验证椭圆曲线算术中的结合律和交换律

结合律和交换律是椭圆曲线算术的重要性质。我们可以执行算术运算在随机点上并检查结果是否满足这些性质。

在 SageMath 中，我们可以这样验证结合律和交换律：

P = E.random_element()
Q = E.random_element()
R = E.random_element()

## 验证结合律: (P + Q) + R == P + (Q + R)
print((P + Q) + R == P + (Q + R))

## 验证交换律: P + Q == Q + P
print(P + Q == Q + P)

可视化椭圆曲线算术操作

为了更好地理解椭圆曲线上的算术操作，我们可以通过图形可视化点加法、点翻倍和标量乘法的过程。

在 SageMath 中，我们可以绘制椭圆曲线和参与算术操作的点：

p = 13
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])

def plot_points_on_curve(E, points, labels, colors):
    curve_plot = plot(E, xmin=-5, xmax=5, ymin=-5, ymax=5)
    real_points = [(float(pt[0]), float(pt[1])) for pt in points]
    point_plots = [point2d(pt, color=colors[i], size=30, zorder=5) + text(labels[i], pt, fontsize=10, color=colors[i], horizontal_alignment='left', vertical_alignment='bottom') for i, pt in enumerate(real_points)]
    return curve_plot + sum(point_plots)

P = E.random_element()
Q = E.random_element()
R = P + Q

plot_points_on_curve(E, [P.xy(), Q.xy(), R.xy()], ['P', 'Q', 'R'], ['red', 'blue', 'green'])

使用 SageMath 生成的包含点 P、Q 和 R 的椭圆曲线图的示例。

通过可视化椭圆曲线上的算术操作，我们可以更深入理解潜在的数学概念及其在密码学中的应用。

通过掌握这些概念和技巧，你将为探索椭圆曲线密码学中的更高级主题（如密钥交换、数字签名和安全通信协议）做好充分准备。

在 SageMath 中使用椭圆曲线

SageMath 是一个强大的开源数学软件系统，提供了大量支持用于操作椭圆曲线的功能。在这一部分，我们将覆盖以下主题：

使用 SageMath 定义和可视化椭圆曲线
发现椭圆曲线上的点
在 SageMath 中操作椭圆曲线群

使用 SageMath 定义和可视化椭圆曲线

要在 SageMath 中定义椭圆曲线，我们可以使用 EllipticCurve 函数，该函数接受一个系数列表 [a, b]，对应于曲线方程 $y^2 = x^3 + ax + b$：

a, b = -1, 1
E = EllipticCurve([a, b])

为了可视化椭圆曲线，我们可以使用 plot 函数：

plot(E, xmin=-5, xmax=5, ymin=-5, ymax=5)

使用 SageMath 生成的椭圆曲线图的示例。

发现椭圆曲线上的点

要找到椭圆曲线上的点，我们可以使用 points 方法，该方法返回有限域内曲线上的点列表：

p = 13
F = IntegerModRing(p)
E = EllipticCurve(F, [0, 7])
points = E.points()
print(points)

输出：

[(0 : 1 : 0), (7 : 5 : 1), (7 : 8 : 1), (8 : 5 : 1), (8 : 8 : 1), (11 : 5 : 1), (11 : 8 : 1)]

在 SageMath 中操作椭圆曲线群

椭圆曲线具有内在的群结构，使我们能够在点之间执行算术运算。SageMath 提供了多种方法来操纵椭圆曲线群，例如点加法、点翻倍和标量乘法。

点加法

要在椭圆曲线上添加两个点，我们可以使用 + 操作符：

P = E.random_element()
Q = E.random_element()
R = P + Q

点翻倍

要在椭圆曲线上双倍一个点，我们可以使用 * 操作符：

P = E.random_element()
R = 2 * P

标量乘法

要对一个点执行标量乘法，我们可以使用 * 操作符：

P = E.random_point()
k = randint(1, E.order() - 1)
R = k * P

多标量乘法

在 SageMath 中，我们可以使用循环与 + 和 * 操作符执行多标量乘法：

points = [E.random_element() for _ in range(5)]
scalars = [randint(1, E.order() - 1) for _ in range(5)]

R = E(0)  # 将 R 初始化为椭圆曲线群的恒等元素
for i in range(len(points)):
    R += scalars[i] * points[i]
print(" 多标量乘法: ", R)

或者，我们可以使用 sum 函数和列表推导来实现相同的结果：

R = sum(scalars[i] * points[i] for i in range(len(points)))
print(" 多标量乘法: ", R)