关于发行政策的务实终局 - 权益证明/经济学
- 以太坊中文
- 发布于 2024-10-28 15:51
- 阅读 773
文章讨论了以太坊发行政策的终局,提出了一个务实的方案,旨在既能阻止 stake 的增长,又能保证适当的共识激励,并为勤奋的 solo staker 提供积极的定期奖励。文章探讨了不同的奖励曲线,并提出了一个具体的框架,即每年的发行量不超过流通量的 0.5%。
由 Anders Elowsson 撰写
感谢 Vitalik Buterin, Caspar Schwarz-Schilling 和 Ansgar Dietrich 的反馈。
1. 引言
本文介绍了一种关于增发策略的实用终局(endgame),该策略可以在保证适当的共识激励并为勤奋的小型单独质押者提供积极的定期奖励的同时,阻止质押量的增长。图 1 概述了终局奖励曲线的两个可能范围。一个硬 终局(hard endgame)(红色)带有一个奖励曲线,通过将收益降至负无穷来限制质押量,但代价是分析、实施和政治复杂性(一个 硬 限制可能难以实施)。即使将增发收益设置为零也会引入额外的复杂性,如果可能的话,最好避免这些复杂性——特别是如果没有 MEV 销毁机制,使得 0% 的增发收益仅停止定期奖励,而不定期奖励会继续存在。确定性可能是可行性的敌人,因为将质押收益降低到较低但依然为正的水平,在所有可能性下,就足够了。本文强调可行性:一个实用 终局(绿色),对目前可以实施的质押量提供概率保证。
图 1. 两种终局的增发范围:绿色表示实用 终局,在近期内可行且更容易达成一致意见;红色表示硬 终局,具有更高的分析和政治复杂性,可能会迫使单独质押者获得负的定期收益。两种终局在低质押存款规模 (DD) 下重叠,因此,在对在不同质押收益下提供质押的意愿做出合理假设的情况下,可能会导致类似的均衡结果。
好消息是,无论采用哪种确切的终局策略,我们都可以对每年发行的流通供应量的最大比例提供更严格的保证。对于以太坊的用户来说,对原生 ETH 代币的发行进行严格限制是可取的,因为它限制了通货膨胀率。由于协议的收入可以被销毁,就像今天部分完成的那样,ETH 的通货膨胀率可以持续为负(通货紧缩)。以太坊可以拥有无需信任的健全货币,同时保留经济安全性——这对于去中心化经济来说非常有价值。社交上限可以设定为 i=0.5\%i=0.5% 的增发率,如图 1 中的灰色线所示。这是一个易于理解的概念(模因性),足以确保一个可行的质押集合,为共识和合并激励提供充足的空间,并允许根据社区的意愿灵活地控制质押量。
一个潜在的实用终局剩下的工作是就奖励曲线的确切规范达成一致,并概述如何在奖励曲线下设计相关的微观激励。该曲线应大致遵循具有缓和增发的奖励曲线的形状。然而,如果目标是通过单一的增发策略变化来实现实用终局,则在较低质押量下的稍高收益和在较高质押量下的稍低收益似乎更可取。沿着这些思路提出了一些选项,峰值增发率为 0.5%。三次方的奖励曲线(图 3 中的红色)可以被强调为符合首选范围,但也应考虑其他曲线(例如,图 3 中的紫色和橙色)。可以选择现在简单地将增发率设置为 0.5%(图 9 中的虚线),并在几年后再次重新审视这个问题,但这似乎更难获得社区的支持。该帖子最后提出了一系列社区和研究人员应该权衡的开放性问题。
2. 增发减少回顾
首先简要回顾一下增发策略和减少增发的可能性;要获得更深入的理解,请阅读 FAQ。
2.1 动机
目前,大约有 3500 万 ETH 被质押,可以说是已经超过了所需的数量,并且质押量正在随着质押成本的降低以及质押摩擦的克服而缓慢增长。减少增发有两个根本原因:
- 目前的奖励曲线迫使用户承担比确保以太坊安全所需的更高的成本(成本广义地定义为包括硬件、风险、流动性不足、税收等)。减少增发通过降低这些总成本来提高福利,如 FAQ 中 图 1 和 图 26 所示。
- 在去中心化经济中,拥有无需信任的健全货币作为主要货币是有价值的。高增发可能会导致流动性质押代币(LST) 主导货币。较低的增发确保了应用程序开发人员和用户不会受到 LST 发行人的垄断压力,或者不必要地冒着 LST 失败的风险,甚至可能在 LST 变得 “ 太大而不能倒” 时威胁到共识。
2.2 影响
在讨论增发并思考对质押者的影响时,重要的是要记住质押供应曲线是向上倾斜的。因此,当收益降低时,均衡收益只会下降名义降幅的一小部分(参见 此帖子中的图 2)。此外,对质押者重要的是他们获得的 ETH 总量。较高的增发也会稀释质押者,如果一些质押者离开,剩余的质押者可能会获得更高比例的 ETH 总量,这符合 最低可行增发(MVI)帖子中的方程式。总 ETH 获得的比例的变化有时也被称为 “ 实际收益”。可以使用同比例图来说明这种影响,也可以使用 1D 的示例 (1, 2)。另一种说明方法是在 MVI 上的线程中提出,该线程在一个图中试图捕捉减少增发如何增加福利(所有组的情况都更好),增加质押者获得的所有 ETH 的比例,并在均衡状态下适度降低名义收益。
内生收益和外生收益
重要的是要理解以下两者之间的区别:
- 内生收益,构成来自参与共识过程的质押奖励,例如增发、MEV、预确认的销售以及对于质押的空投;以及
- 外生收益,构成来自共识参与之外的奖励,例如 DeFi 中的以重新质押收益形式的奖励。
在辩论的早期,有人担心,例如,重新质押会使单独质押在以较低数量的质押执行的均衡状态下变得不可能。其动机是,委托质押者能够更好地获得外生收益。虽然这种普遍担忧有一些道理,但外生收益也可以直接从非质押的 ETH 中获得。因此,如果内生收益接近于零,那么除了保护或攻击以太坊之外,任何人都不会有任何激励进行质押——对于单独质押者和委托质押者来说都是如此。
2.3 缺点
然而,减少增发可能不仅带来好处。一个担忧是,由于单独质押者具有较高的固定成本(例如,硬件),因此他们对质押收益的降低更为敏感。因此,降低增发可能会在一定程度上降低单独质押者的比例(回顾 图 11 中保留收益的差异如何改变图 13 中单独质押者的比例)。这是一个潜在的缺点,必须权衡减少增发的好处,但也有反驳指向另一个方向。还应该注意的是,当增发随着质押参与度的增加而下降时,阻挠攻击 (1, 2) 和卡特尔化攻击的几率增加。
此外,如果增发减少到低于 MEV 的水平,尤其是在接近于零或负数时,共识激励将受到负面影响,并且无法轻松汇集其 MEV 奖励的质押者(即单独质押者)之间的质押收益变动性将会增加。由于这些原因,实施 MEV 销毁机制(例如,1, 2, 3, 4, 5)非常重要——但这种机制可能离采用还有很长的路要走。如果例如提议者和构建者可以合作以降低经证明的 MEV (1, 2, 3),也可能无法销毁所有 MEV。但是,竞争中的质押者有强烈的动机与构建者集成,以使出价保持在相当高的水平,从而保持较高的销毁量。
在较低增发量下缺乏共识激励可以通过增加对错过证明的惩罚来弥补。然而,如果最大增发量为零(即,每次增量的基本奖励为零),则这种相对调整无效。增加证明惩罚的体制也将为少数人阻挠攻击打开大门,其中提议者有选择地删除证明以损害竞争中的质押者。如果提议者惩罚适用于补偿,那么错过的提案对于离线的单独质押者来说将变得相当昂贵,他们也会由于增加的证明惩罚而遭受相对较高的损失。然后可以考虑诸如如果提议者在前 2-4 个 epoch 中处于不活动状态则减少惩罚之类的补救措施,但是设计复杂性会增加。
在过渡到 Orbit SSF 下的合并激励也可能受到增发减少的负面影响。有充分的理由像今天一样在 Orbit SSF 中根据质押分配提案权,至少在仍然有 MEV 可提取的情况下是这样。否则,如果合并的验证者是首选的,那么就很难保留公平性,因为协议不知道预期的 MEV 收入。如果提案权根据质押分配,并且预期的证明收入较低或为负,那么质押者就有强大的动机去合并并降低他们的活动率,因为这降低了罚没的风险。然后增加的证明惩罚就不那么重要了,因为质押者可以简单地通过运行许多小型验证者来确保他们主要处于不活动状态。
为了确保合并,必须追求相对实质性的个体激励,至少在 MEV 销毁机制到位之前是这样。这意味着在极低或零增发的情况下,小型单独质押者必须在等待提议机会的每个 epoch 损失 ETH。根据第 2.2 节的推理,小型验证者的预期内生收益仍然为正,但无法轻松汇集奖励的单独质押者会受到奖励中相对较高的方差的影响。更复杂的选择是在合并级别较低且没有 MEV 销毁的情况下,将相对较多的区块提案分配给合并的质押。
根据定义,如果验证者集合没有合并,集体合并激励也会进一步减少已经在较低基线上的增发,再次可能将单独质押者推向负数区域。
3. 实用终局
3.1 奖励曲线的作用
以太坊的共识机制依赖于一个奖励曲线,该曲线规定了在质押一定数量的 ETH 时,执行每次验证者职责应该奖励多少 ETH,从而有效地确定了在完美参与下的最大总增发量。一旦安全性得到巩固,奖励曲线应大致反映增加额外质押的边际效用递减。具体而言,它应该被设计为“增发策略扩张路径”,可以最佳地平衡相关的权衡。它可以理解为沿着可能的供应曲线的效用最大化首选均衡点轨迹。换句话说,当可以实现更理想的均衡时,奖励曲线不应在供应曲线上产生不太理想的均衡点。因此,保证某些特定数量的质押的 PID 控制器是不可取的;它无法准确地衡量长期增加额外质押的边际效用。
3.2 终局类别
已经讨论了各种增发终局的方法;在增发减少 FAQ 中强调了五个大致划分的类别。
类别 4 已被称为 经济上限,目标或质押上限收益接近负无穷。最近在一篇广泛的 文章 中讨论了这一点。其好处是绝对保证了可以限制质押量,即使在 MEV 存在的情况下也是如此。这种方法的潜在缺点是,当然在上限设置较低的情况下,均衡收益对于单独质押者来说可能变得没有吸引力,特别是如果没有 MEV 销毁来减少奖励变化(如第 2.3 节中所述)。另一个问题是促进负收益所需的额外逻辑(例如,每个 epoch 扣除的 质押费)。此帖子 中的图 10 显示了在质押费下,单独质押者定期收入为负的真实情况。第三个缺点是,负增发收益会由于每次调整微观激励时增加的分析和实施复杂性而产生“共识设计债务”。图 1 概述了我认为适合类别 4 设计的大致范围,上限达到了所有 ETH 质押量的 2/3 或 3/4 左右。该图将其称为“硬 终局”,因为它具有复杂性和硬性上限。
类别 2 涉及到更适度的增发减少。它代表了近期内可取的那种减少类型,并且不需要结合额外的逻辑来维护适当的共识激励。它已被提议作为第一步,然后是类别 4 的更改。有关使用缓和增发的奖励曲线的更详细介绍,请参见此处。虽然这种类型的奖励曲线很可能在很长一段时间内都可行,但潜在的缺点是缺乏近乎确定性。
类别 3 占据了两种方法之间的中间地带,其中保留正增发收益的曲线最相关。当质押太多的 ETH 时,增发会降低到非常低的水平,但仍为正值。虽然共识/合并激励和单独质押可能会变得紧张,但勤奋的单独质押者无需“支付质押费用”即可等待提议区块的机会,并且“共识设计债务”较低。如果目标是对增发进行一次近期的调整,并且该调整有很大可能无限期持续,那么这就构成了一个实际的终局。实际上,类别 2 和类别 3 之间的差异相对较小,因为它们可能会导致类似的均衡结果。但是,如果在较高数量的质押下,将增发收益设置为最低(正)水平,则可能有助于提高瞄准终局的概念的可信度。
有人认为,以太坊必须以最终需要的最后一次更改为目标,对增发策略进行一次更改。我个人认为,分阶段方法有很多好处。如果社区愿意将奖励曲线设置为 0.5% 的增发率,并承诺在几年后重新审视该问题,我将支持它。这样可以简化近期的流程。但是,增发变更的政治性质和社区反应似乎支持通过一次更改来执行终局政策。
由于质押的固有成本和外生收益的有限相关性,类别 3 的变更提供了一个可信的理由,使其成为所需的最后一次货币政策变更。那么责任就落在了开发人员身上,他们需要采取行动以实施 MEV 销毁。MEV 销毁机制将:(1) 缓解在高质押量下由于低增发而对共识设计参数造成的压力,以及 (2) 使较低的均衡质押量更有可能实现。另请注意,建立类别 4 的质押上限并不能排除将来更改的必要性。当以太坊旨在平衡增发策略的权衡时,质押量并不是唯一发挥作用的因素。实际上,从现在起二十年的主要问题可能与今天的重点大相径庭,就像我们目前面临的许多问题在几年前也未曾预料到一样。因此,像任何其他策略一样,质押上限增发策略可能需要逆转。在这种情况下,逆转更可能是以增加增发的形式出现,这是以太坊迄今为止一直避免的方向。
3.3 实用终局的首选增发范围
图 2 大致概述了实用终局奖励曲线的首选范围(先前在图 1 中以绿色显示)。此范围代表了我个人的偏好,因为它具有合并/共识激励的早期草图。其他人可能有不同的偏好,应进行整理和进一步辩论。激励设计的草图也可能会演变,从而导致对该范围进行较小的调整。绿色的虚线曲线是先前提出的具有缓和增发的奖励曲线。如果要求是终局,那么在较高的存款规模下降低成本似乎是合理的。首选范围建议,如果每个人都进行质押,则仍然发行至少 6 万个 ETH(增发收益约为 0.05%),并且最多增加 10 万个 ETH(16 万个 ETH)。我的观点是,只有在 MEV 比今天高得多的情况下,才能在这种水平上接近均衡。该想法是,最后一小部分潜在的质押者具有相对非常高的保留收益(需要相当高的质押收益来进行质押),这应以概率方式进行考虑。较低的正增发可能不会对均衡产生太大影响,同时可能需要我们让小型单独质押者在 MEV 存在的情况下获得负的定期奖励,这我认为是不可取的。
图 2. 实际终局增发策略的质押存款规模 DD 增发的首选范围(个人粗略观点)。该策略应确保在低存款规模时提供足够的增发收益(但不超过),并且在较高的存款规模时,应确保如此低的增发收益,以至于极不可能达到均衡。为了提高可行性,在整个过程中仍将发行量保持在正数水平。
例如,假设开发人员无法建立 MEV 销毁,并且当 MEV 每年为 60 万个 ETH 时,达到了高存款规模的均衡(长期平均水平的两倍可能完全可以实现)。无论是发行 0 个 ETH 还是 10 万个 ETH,都不会从根本上改变均衡。至少对于委托质押者而言,增发的重要性肯定会降低,因为委托质押者可以轻松地获得汇总的 MEV 奖励。但是,如果增发是 0 个 ETH 而不是 10 万个 ETH,这大概需要对微观激励进行更大的重新设计,并将迫使单独质押者支付质押费用,以希望有机会提议区块。如果建立了 MEV 销毁,那么无论如何都不会在这里达到均衡,因此发行 10 万个 ETH 的意义仍然不大。根据以下直觉定义了首选范围的上限:
- 对于以太坊用户而言,将增发率限制为 0.5% 可能是可取的(请参阅第 3.4 节),这在质押 1500 万个 ETH 时会产生高达 4% 的增发收益,在质押 2000 万个 ETH 时会产生高达 3% 的增发收益,在质押 3000 万个 ETH 时会产生高达 2% 的增发收益。
- 由于超过一定水平的额外安全性的效用递减,增发率大概不应保持固定在 0.5% 的终局政策上。因此,从目前的存款规模 (3500 万个 ETH) 或更低的水平开始进一步减少似乎是可取的。
- 在最大数量的质押下,增发不应高于绝对必要值,因为这种均衡是多么不受欢迎。超过 16 万个 ETH(约为此帖子中测得的年度 MEV 的一半;增发收益率为 0.133%)似乎过高了——合理地应该可以设计出低于该水平的可行共识/合并激励。
大概第一小部分质押者具有相对较低的保留收益(需要相当低的收益来进行质押),这也应以概率方式进行考虑。但是,如果奖励曲线必须永远保持不变,以太坊应该发行略多于在所需的存款规模下实现均衡所需的代币。原因是 MEV 最终可能会被销毁,这必须考虑在内。如果考虑到当前关于所需存款规模的想法,那么在较低数量的质押下,将增发量保持在或理想地高于绿色虚线曲线似乎是有益的。
然后,一个问题是随着存款规模的增加,增发应以多快的速度下降到某个最低可接受水平。我在此处的观点是,将增发率保持在 0.1% 以上直至至少一半的 ETH 被质押是合理的。原因是 0.2% 的质押收益率(在质押了 6000 万个 ETH 的情况下,增发率为 0.1%,并且有 MEV 销毁)可能对以太坊产生更大的影响,例如,从对去中心化的影响方面来看,超过了一半的 ETH 被质押的事实。这符合第 3.1 节中概述的理念——评估沿着向上倾斜的供应曲线的不同均衡的效用。当然,在这种低收益率和质押 6000 万个 ETH 的情况下建立均衡的可能性很小,但仍然必须评估该情况下的假设性选择。
3.4 有形框架:永不超过 0.5% 的增发率
理想情况下,实用的终局应将选定的奖励曲线定位在一个易于理解的有形框架内。图 1 和图 2 中上方的灰色线表示每年发行流通供应量的 0.5%,即增发率 i=0.005i=0.005。从沟通的角度来看,承诺每年发行不超过流通供应量的 0.5% 是一项易于理解的政策,具有“模因”品质。稍微放宽一些,它也适合以太坊中流行的“2 的幂”框架:最多 2^{-1}2−1% 的供应量。请注意,该框架不仅适用于实用的终局奖励曲线;它旨在永久适用。即使将来推动增发变更,也可能仍然存在一项现有的社会承诺,从而使将增发率提高到 0.5% 以上特别难以推动。虽然对流通供应量的上限是一种站不住脚的货币政策,但对增发率的上限则不然。但是,它具有相同的简单性。
流通供应量将漂移以平衡供应、需求和协议收入。因此,一旦在共识层开始跟踪流通供应量,该承诺最终将通过在奖励曲线的方程式中交换 DD 和 dd 并通过包括交换时的流通供应量来进行标准化来执行。
4. 实用终局奖励曲线
本节提出了实用的终局奖励曲线,并进一步分析了以太坊面临的权衡。示例将构建为在 i=0.5% 处达到峰值,但如果需要,可以通过更改比例参数(通常表示为 k)来调整此峰值。 特别是,任何曲线的峰值都可以略微降低,同时仍保持在 i=0.5% 以下。
4.1 经典调和
发行量
图 3 提供了使用经典调和机制的示例。 这些奖励曲线的特殊构造最初的动机是其最小规范更改,以及确保在任何时候都不会增加发行量。 此外,请注意,考虑到阻挠攻击(1,2)和卡特尔攻击,发行量的平稳衰减是可取的。
绿色奖励曲线是通过将当前奖励曲线的公式除以 1+D/k 来构造的,其中 k 也表示峰值 质押 参与度。 可以通过对 D 进行指数运算来改变曲线的形状,并且可以通过更改 k 来改变峰值位置(比例)。 虚线绿色曲线与图 2 中显示的曲线相同,而完整绿色曲线会增加 k,以便曲线在 i=0.5% 处达到峰值,这是灰线标记的水平。 图中其他颜色的曲线是通过以 0.5 为步长增加指数直到 3.5(对于黄色曲线)来构造的,调整 k 以始终在 i=0.5% 处产生峰值。 因此,紫色曲线是通过除以 1+(D/k)^2 来构造的。 峰值将位于 D=k\sqrt{3} 处,并且在这种情况下,变量 k 设置为 40\times10^6,以在 i=0.5% 处产生峰值。 在常见问题解答的图 15 中,紫色曲线反而依赖于略低的 k 设置。
图 3. 通过更改添加到当前奖励曲线公式分母中的项中 D 的指数运算构建的可以调和发行量的奖励曲线的可能形状。 图 2 中首选的范围以灰色表示。
哪个奖励曲线是最佳的将取决于应如何平衡第 2-3 节中讨论的各种权衡,这自然会受到不同意见的影响。 红色奖励曲线是唯一仍然完全在图 2 中提出的首选范围内的选项,但是橙色和紫色奖励曲线也几乎在该范围内。 推测地,可能最容易就这三种形状之一达成协议,并根据需要进行缩放。
请注意,对于红色奖励曲线,添加项中 2.5 的指数运算自然会与当前奖励曲线的 0.5 的指数运算相结合。 因此,发行量收益的最终公式可以简单地重写为:
y_i = \\frac{cF}{\\sqrt{D} + (D/k)^3},它只需要调整 k。 具体来说,对于绘制的曲线,k 必须从大约 35.4\times10^6 降低到 1.95\times10^6。 因此,我们可以将红色形状称为“立方”奖励曲线,将橙色形状称为“立方+”奖励曲线,然后将紫色形状表示为“平方+”等。 黄色曲线是通过将先前公式中的指数从 3 增加到 4(因此表示为“四次”)来创建的。 该奖励曲线使发行量在高 质押 量时非常接近于零。
包含 MEV 的 质押 收益
图 4 显示了 质押 收益,包括每年 30 万 ETH MEV(大致为长期平均值),用于图 3 的奖励曲线。为了使讨论更具体,在假设的蓝色供应曲线下的均衡用圆圈标记,从而提供了几年后的合理情况。 请注意,由于决定 质押 的摩擦(即使忽略存款队列),供应曲线在短时间范围内几乎是垂直的,但随着时间的推移而弯曲,这里的重点是长期。 假设的供应曲线将导致 质押 的 50M ETH 的均衡,并且在当前奖励曲线下的收益率为 2.9%。
其他奖励曲线产生了在 质押 的 34M-40M ETH 内的均衡,并且收益率为 2-2.3%。 考虑一个极端的低收益情景可能会很有趣,其中供应曲线远低于最可能的结果 - 也许是十年或二十年后。 虚线蓝色线表示了这样的假设供应曲线。 希望能够达成广泛的共识,即在这种情况下,当前奖励曲线下的均衡是不希望的。 在大约 1.9% 的 质押 收益率下,发行量为 170 万 ETH - 如此之高,以至于它位于图 1-3 的边界之外。 此外,以未 质押 的 ETH 形式存在的以太坊经济体中也不再存在无需信任的健全主要货币。 与在较低 质押 量下强制执行的均衡相比,所有 ETH 或其衍生品的持有者可能会更糟。
图 4.对于不同形状的调和奖励曲线,包括每年 30 万 ETH 的 MEV,在内 质押 收益率。 使用几年后的假设供应曲线(蓝色)的均衡用圆圈表示。 一种不太可能非常低的供应曲线也用虚线蓝色线表示,假设的均衡用正方形表示。
轮廓奖励曲线的均衡 质押 量在 57M-80M ETH 之间变化,并且供应曲线非常低。 这高于希望的水平。 但是,这确实是一个极端情况,其中 MEV 燃烧尚未实现,并且一半的代币持有者已准备好在总 质押 收益率为 0.75% 的情况下承担 - 直接或通过委托 - 质押 的成本。 进一步减少发行量以调和 质押 可能是不希望的。 黑色虚线表示根本没有发行量的结果。 在我看来,与较低的奖励曲线均衡相比,均衡 质押 量并没有大幅度减少,因此这种方法是不必要的牺牲,会降低单独 质押 的可行性并增加共识设计的复杂性(另请参见第 2.3 节和第 3 节)。
发行量收益
相反,图 5 显示了没有 MEV 的发行量收益,这可能是包含完全成功的 MEV 燃烧机制之后的情况。 在调查的奖励曲线下的均衡最终在轮廓假设供应曲线下 质押 的大约 30M ETH 处结束。 即使在非常低的供应曲线下,均衡也会降至 39M-57M ETH 之间:如果发行量收益保持为正数,MEV 燃烧将是实现低 质押 量的关键组成部分。
图 5. 不同形状的调和奖励曲线的发行量收益,在完全 MEV 燃烧下,这也将是 质押 收益。 使用几年后的假设供应曲线(蓝色)的均衡用圆圈表示。 不太可能非常低的供应曲线也用虚线蓝色线表示,假设的均衡用正方形表示。
4.2 发行量下限
还可以设计奖励曲线,以从当前奖励曲线平稳过渡到发行量下限 I_f,并设置为某些所需的水平。 图 6 中显示了三个示例。 浅蓝色曲线是通过与 sigmoid 加权混合计算得出的:
w = \\frac{1}{1 + 2^{(D - D\_c)/-k}}.混合的中心点设置为 D_c=32\times10^6,过渡的陡峭度设置为 k=7\times10^6。 可以根据需要进行调整。 然后,曲线混合 (1-w)I_r+wI_f,其中 I_r 是当前奖励曲线的发行量 [即,I_r(D)],而 I_f 是设置为 120,000(i=0.1%)。 另一个解决方案是简单地通过替换 I_r 来在最大和最小所需的发行量水平之间进行混合,例如,固定的 600,000 ETH。 这可以通过粉红色曲线来完成,从而说明了在 sigmoid 加权拦截当前奖励曲线的点处从该曲线进行过渡的分段选项。
第三个选项是使用希尔型方程式:
Y(D) = \\frac{D\_{h}^{n}I\_r + D^{n}I\_f }{D^{n} + D\_{h}^{n}}.这是一个相当干净的构造,依赖于在 I_r 和 I_f 之间指定的中间点 D_h,以及进一步确定形状的指数 n。 棕色曲线由 D_h=30\times10^6 和 n=3 构造,设置 I_f=90,000。
图 6. 三个渐近接近 i=0.1% 左右的发行量下限的奖励曲线。 图 2 中概述的首选范围再次以灰色表示。
图 7 显示了包括每年 30 万 ETH MEV 在内的 质押 收益,并调查了与图 4 相同的功能。具有发行量下限的奖励曲线为低供应曲线提供了约 60M ETH 的均衡 质押,与先前示例的橙色奖励曲线大致一致。 由于发行量保持在下限附近固定,因此在较高 质押 量下,MEV(“无发行量”)相对于发行量 + MEV 的比例保持近似恒定。 相反,图 8 显示了仅有发行量收益的结果。
图 7. 对于渐近接近发行量下限的奖励曲线,包括每年 30 万 ETH 的 MEV,的 质押 收益。 使用几年后的假设供应曲线(蓝色)的均衡用圆圈表示。 不太可能非常低的供应曲线也用虚线蓝色线表示,假设的均衡用正方形表示。
图 8.渐近接近发行量下限的奖励曲线的发行量收益,这也将是完全 MEV 燃烧下的 质押 收益。 使用几年后的假设供应曲线(蓝色)的均衡用圆圈表示。 不太可能非常低的供应曲线也用虚线蓝色线表示,假设的均衡用正方形表示。
4.3 分段构造
平滑的奖励曲线并不完全与美学有关。 确保没有可能影响 质押 决策的不连续性似乎是合理的,例如,使卡特尔攻击在某些特定范围或点上更具吸引力。 总体发行政策扩张路径也可以说是平滑的。 但是,线性分段构造带来了简单性的好处,并且缺点可能不足以放弃。 图 9 显示了三个线性构造。 在 0.5% 和 0.1% 的发行率之间,深蓝色和青色奖励曲线每 质押 100 ETH,发行量减少 1 ETH。 相反,米色奖励曲线围绕 60M ETH 的中点对称,每 质押 125 ETH,发行量减少 1 ETH,同时将发行率从 0.5% 降至 0.1%。
这些构造提供了一些切实的锚点,可以简化通信。 发行量总是很容易计算的,并且在 0.5% 的发行率下,在 质押 的 15M ETH(供应量的 1/8)时,发行量收益变为 4%,在 20M ETH(1/6)时变为 3%,在 30M ETH(1/4)时变为 2%。 对于深蓝色和青色奖励曲线,发行量收益率分别在 40M ETH 或 45M ETH 处达到 1%,并且在 60M ETH(1/2)处,发行量收益率分别为 0.33% 或 0.5%。
虚线深红色奖励曲线仅将发行量设置为 0.5% 的发行率。 这种类型的奖励曲线被称为“上限发行量”,并且在 Vitalik 在 2021 年初的提案中暗示了这一点。 它不一定是终局策略,必须理解为我们可能会在几年后再次回到对话中。 它将使我们能够解决 质押 量增长的问题,以便我们可以专注于其他主题几年 - 直到与 MEV 和 Orbit SSF 相关的扭结得以解决为止。 如前所述,我发现这种类型的解决方案很有吸引力,但是从社区的角度来看,似乎对明确的答案有明显的胃口。
图 9. 说明了发行量线性变化或保持固定的分段构造。
5. 结论和重要问题
与提供 99.9% 确定性的发行政策相比,确保 100% 确定性将 质押 量调和到合理水平的发行政策存在一些缺点。 本文提出了实用的终局奖励曲线,这些曲线将调和 质押 量的增长,而不会引入不必要的政治,分析和实施复杂性。 我个人的偏好是在概述的首选范围内,是使用第 4.1 节中提出的橙色,红色或紫色调和奖励曲线的形状,其中红色曲线完全在首选范围内。 这些曲线使得在高 质押 量下实现均衡的可能性非常小,但是可以使小型单独 质押 者在充分履行职责时始终获得积极的常规奖励。 我认为,简单地将发行量设置为 0.5% 的发行率,如红色虚线所示,也是一个有吸引力的解决方案。 想法是,如果需要,在几年后再次回到对话中,一旦解决了MEV燃烧等各种问题。 但是此解决方案可能对以太坊社区没有吸引力。
实用终局的一个明显好处是,它具有更少的依赖关系,并且如果 MEV 燃烧在低供应曲线下没有实现,它也不会失败。 这使我们能够解决发行量问题而没有不必要的延迟。 与此相关的是,专注于不切实际的情况(例如,每个人都以接近零的发行量收益率进行 质押)是不幸的,因为当一项更改非常有益时,我们可能无法前进。
面向社区和研究人员的问题
欢迎社区提供反馈和辩论。 例如:
- 只要单独 质押 者从不常见的区块提案中获得长期的积极预期收益,是否允许不合并区块提案奖励的单独 质押 者在积极证明时损失 ETH? 是否应严格避免这种情况,还是在某些较高的存款规模下,为了阻止进一步增长,比如在 质押 的 60/90/120M ETH 时,是可以接受的? 在一年内离线的百分之多少的情况下,负收益率是可以接受的?
- 在 质押 的 15M,30M,45M,60M,75M,90M 和 120M ETH 时,发行量(或等效地,发行量收益率)应设置为多少? 欢迎社区成员和研究人员指定他们自己的“首选范围”。
- 鉴于当前与 MEV 相关的不确定性以及减少发行量的收益,你是否支持在接下来的 3/4/5/6 年中将发行量简单地固定在 0.5% 的发行率上(图中灰线;图 9 中红色虚线),并承诺在此之后再回到该问题?
从研究的角度来看,鉴于对 MEV 燃烧和 Orbit SSF 的依赖性,通过绘制在特定时间范围内实施这些机制的可能性,似乎可以获得很多收益。 这是我们作为共识研究人员可以做的事情,同时我们勤奋地继续研究实施细节。
- Orbit/Vorbit SSF中的合并激励
- 三层 质押(3TS)- 解绑证明者、包含者和执行提案者
- 以太坊 质押 中的发行政策与结构性事件——分析
- 彩虹角色与激励:ABPS + FOCILR + AS
- 原文链接: ethresear.ch/t/practical...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Builder Codes & ERC-8021:修复链上归属问题 81 浏览
- 并行执行的谎言:为什么SOL和ZERO不是在与ETH竞争,而是在输给它的L2 107 浏览
- “夺旗”竞赛继续! 69 浏览
- DeFi收益是什么以及它是如何运作的?新手指南 100 浏览
- EVM Gas 分析:新的执行跟踪数据 155 浏览
- 质押和链上信贷市场之间的微妙张力 225 浏览
- 以太坊应该停止担心扩展性,去做人们想要的东西 292 浏览
- Vitalik的L2重置:以太坊为何需要此航向修正 231 浏览
- 如何桥接到MegaETH(今天测试网,主网即将上线) 321 浏览
- CoW DAO月度回顾:2026年1月 - CoW DAO 289 浏览
- Vitalik: 重新评估以太坊 Layer2 347 浏览
- lambdaworks 2026 年更新路线图和优先级 304 浏览
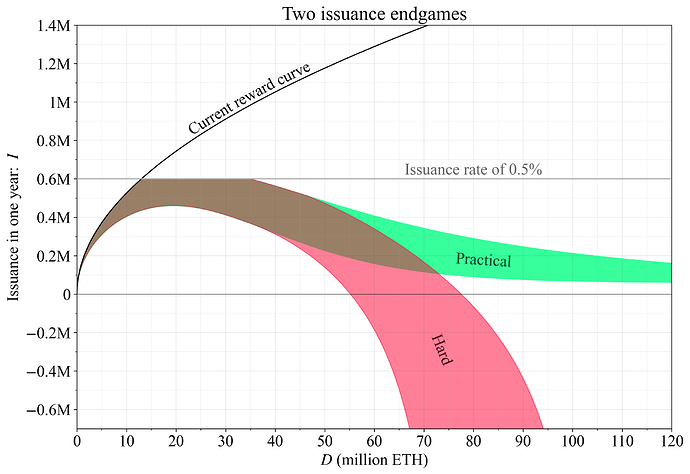 图 13237×2227 388 KB
图 13237×2227 388 KB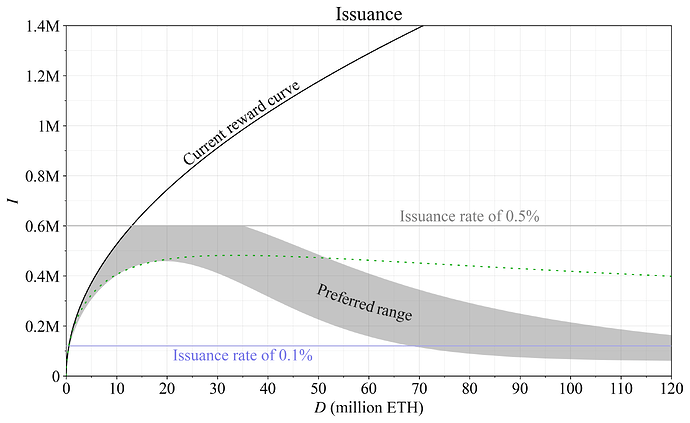 图 23181×1952 298 KB
图 23181×1952 298 KB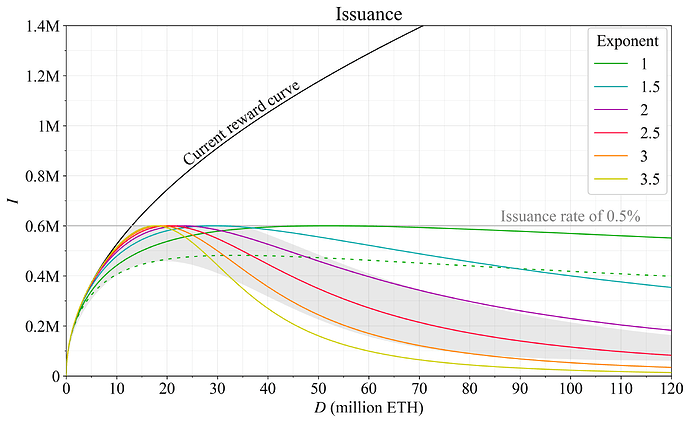 \
图 33181×1952 438 KB
\
图 33181×1952 438 KB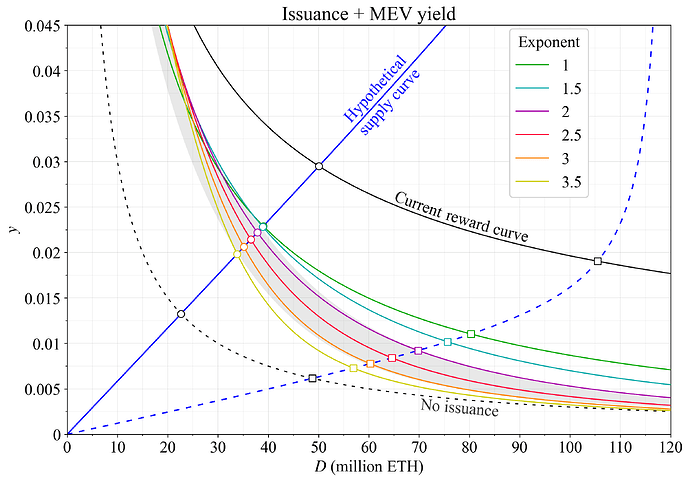 \
图 42446×1709 481 KB
\
图 42446×1709 481 KB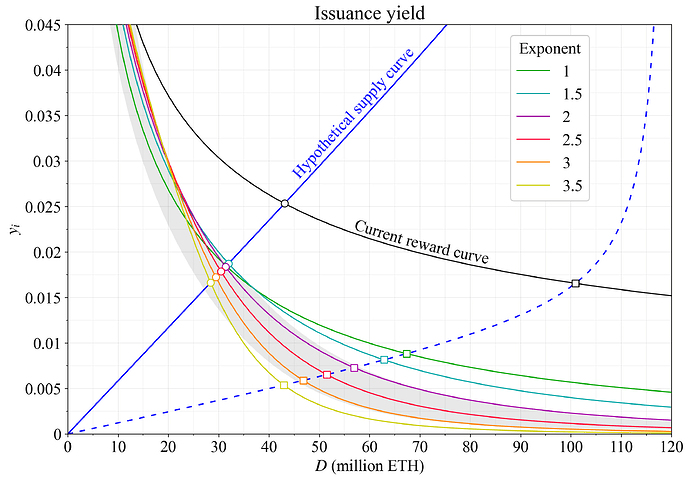 \
图 52657×1856 492 KB
\
图 52657×1856 492 KB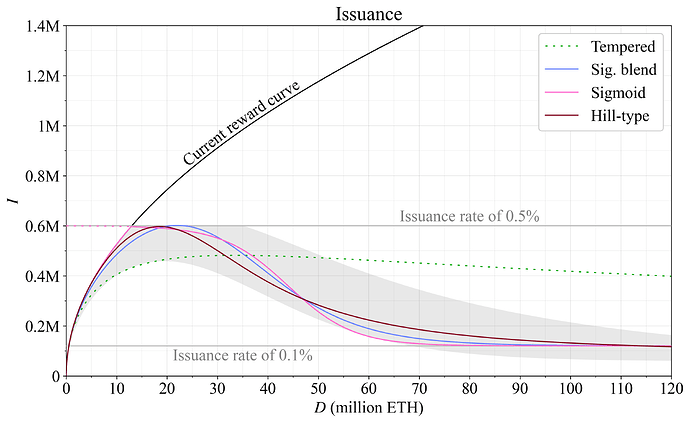 \
图 63181×1952 383 KB
\
图 63181×1952 383 KB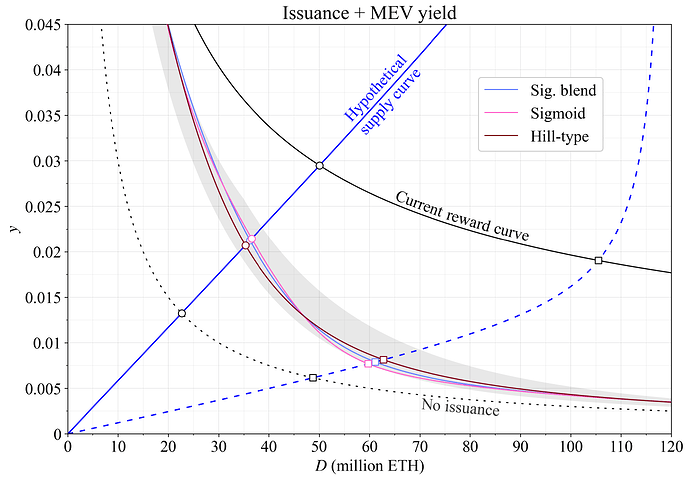 \
图 72764×1929 452 KB
\
图 72764×1929 452 KB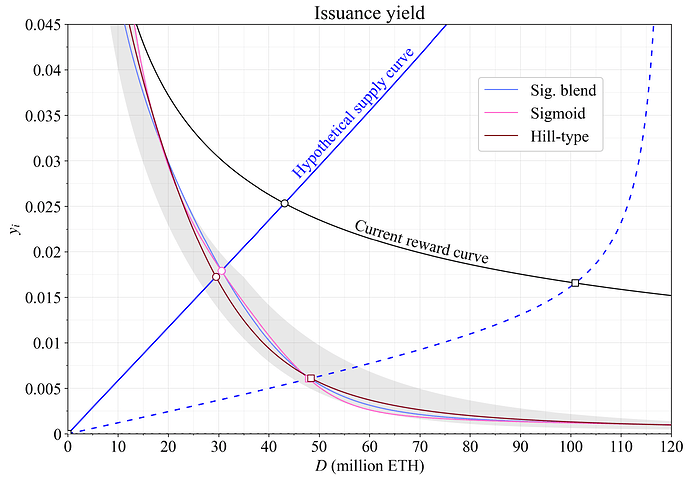 \
图 82764×1929 418 KB
\
图 82764×1929 418 KB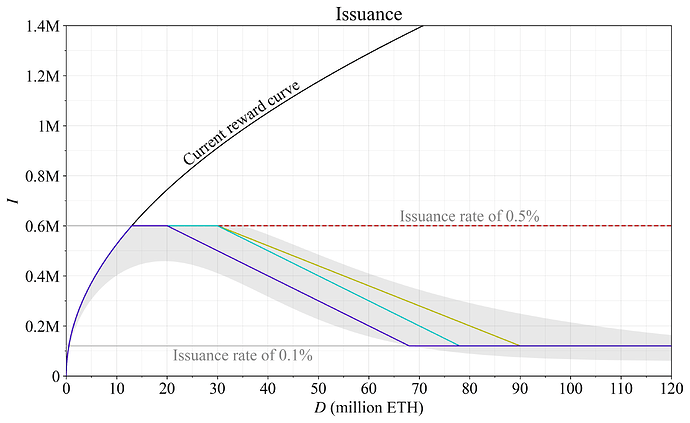 \
图 93181×1952 317 KB
\
图 93181×1952 317 KB
