区块链中的数学 - 哈希承诺

写在前面

上一篇介绍了不经意传输协议，原本打算本文写paillier加密及其同态，但是想想还是后面再说比较好，按循序渐进顺序，先介绍密码学承诺更自然些，

好了，进入正题 --- 密码学中的承诺！

密码学中的承诺

密码学中的承诺不同于日常生活中承诺的含义。日常生活中，通常的承诺一般是保证在XXX日期实现某个既定目标或行为，可以是完成某项作业，取得什么进展等等，有点类似合同的性质，到达一特定时间点兑现预先诺言。比如年底前完成销售额1亿的目标，就是一个承诺。

密码学中的承诺与此不同，它是对一个既有的确定性的事实（敏感数据）进行陈诉，保证未来的某个时间有验证方可以验证承诺的真假，也就是说承诺的标的是当前时间的，未来不会发生变化。

密码学承诺包含承诺方和验证方角色，两个使用阶段。

承诺生成（Commit）阶段： 承诺方选择一个暂不公开的敏感数据v，计算出对应的承诺c并公开。

承诺披露（Reveal）阶段： 也称之为承诺打开-验证（Open-Verify）阶段,承诺方公布敏感数据v的明文和其他的必要参数，验证方重复承诺生成的计算过程，比较新生成的承诺与之前接收到的承诺c是否一致，一致则表示验证成功，否则失败。

密码学承诺具备两个特性：

隐匿性（hiding）： 做出的承诺是密文形式，在打开承诺之前，验证方不知道承诺方的敏感数据。 绑定性（binding）： 一旦承诺生成并公开承诺，承诺方不能将已承诺的敏感数据换成（或解释成）另一个不同的数据。

本文之后提到的承诺，不再加以说明，默认均指密码学承诺。接下来介绍一些常用的承诺。

哈希承诺

哈希承诺，用户可以通过以下公式计算关于敏感数据v的承诺，其中H是一个密码学安全的单向哈希算法。

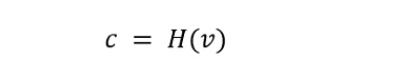
关于哈希（摘要）算法，之前文章中提到并使用多次，虽然我们没有单独对其进行阐述，但是很容易理解，并且能够查到的公开资料非常多，所以没有赘述。

简而言之，哈希算法是一个单向不可逆且对输入敏感的算法。以此为例，对于不同的输入v，得到的哈希结果c也是不同，准确的说，随机输入一个v,得到的唯一的c是均匀分布的，且无法预测即抗碰撞性。

基于单向哈希的单向性，难以通过哈希值H(v)反推出敏感数据v，提供了一定的隐匿性；基于单向哈希的抗碰撞性，难以找到不同的敏感数据v'产生相同的哈希值H(v)，以此提供了一定的绑定性。

举例说明，我有一篇文章将其哈希后结果作为该篇文章的承诺公开，之后任何人要求验证我的承诺，OK，我把原始文章拿出来，对方做一次哈希得到结果等于之前承诺，证明承诺为真。如果我没有那篇文章或者说用别的文章代替，那么哈希结果会发生变化，这样的作弊行为就无法通过验证。这种形式可以作为版权证明的一种方式。

哈希承诺的构造简单、使用方便，满足密码学承诺基本的特性，适用于对隐私数据机密性要求不高的应用场景。

对隐私数据秘密性要求高的场合，哈希承诺提供的隐匿性比较有限，不具备随机性。对于同一个敏感数据v，H(v)值总是固定的，因此理论上可以通过暴力穷举，列举所有可能的v值，来反推出H(v)中实际承诺的v（注：安全性高的哈希函数目前算力破解还很难）。

另外，哈希承诺不具有在密文形式对其处理的附加功能，例如，多个相关的承诺值之间密文运算和交叉验证，对于构造复杂密码学协议和安全多方计算方案的作用比较有限。

小结

本文介绍密码学承诺的含义及性质，并对哈希承诺做了说明，关于hash函数的内在机制实际是比较复杂的，我们以黑盒的角度来学习了解它的性质，在区块链&密码学中，哈希函数占据了基础且重要的位置。 比如区块链中常用的sha256,keccak等哈希算法。

下一节继续介绍安全性和实用性更强的Pedersen承诺。

欢迎关注公众号：blocksight

相关阅读：

区块链中的数学 - 不经意传输 不经意传输协议

区块链中的数学- BLS 基石（双线性函数）和配对 双线性映射（配对）

区块链中的数学 - BLS门限签名 BLS m of n门限签名

区块链中的数学 - BLS密钥聚合 BLS密钥聚合

区块链中的数学 - BLS数字签名 BLS签名及验证

区块链中的数学 - 参与者 < 门限值t的密钥更新Amir Herzberg方案 Amir Herzberg改进方案

区块链中的数学 - Feldman的可验证的密钥分享 Feldman可验证密钥分享方案

区块链中的数学 - Ed25519签名 Ed25519签名

区块链中的数学-ElGamal算法 ElGamal算法签名及验证&实例演练

区块链中的数学-VRF基于ECC公钥体制的证明验证过程 基于椭圆曲线的VRF证明验证过程

Schorr签名与椭圆曲线 Schorr签名与椭圆曲线

区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析（中）