区块链中的数学 - BLS 基石(双线性函数)和配对
- blocksight
- 发布于 2021-01-02 15:55
- 阅读 14282
双线性配对特性不仅可以用于签名构造,密钥协商等,还可以实现乘法的同态隐藏和校验。这一点在零知识证明项目中应用很多。另外需要说明的是,并非基于任何椭圆曲线都可以构造配对函数,对于能有效实现双线性对的椭圆曲线,称为pairing-friendly curves,例如BLS12_381曲线。
写在前面
上一篇讲述了BLS门限签名,BLS签名机制和其他签名方案相比,最大的不同或者说创新在于使用了双线性配对函数,这一点在前面几篇都提到过,本文简要说一下双线性配对函数的性质。
双线性映射定义
双线性配对(Bilinear Pairing), 有时也称作双线性映射,具体翻译略有不同。双线性配对在密码学中得到广泛的应用始于2001年Boneh和Franklin使用它构造了第一个实用并且安全的基于身份加密方案IBE(IBE 可参照https://en.wikipedia.org/wiki/Identity-based_encryption)。 可以看出与BLS首次提出在同一年,不是巧合,是因为二者有共同作者--Boneh教授。
定义:一个双线性映射是由两个向量空间上的元素,生成第三个向量空间上一个元素之函数,并且该函数对每个参数都是线性的
若有A,B,C三个向量空间,映射e: A × B → C是一个双线性映射,则A固定,B可变时,B到C的映射是线性的,B固定,A可变时,A到C的映射也是线性的,也就是说保持双线性映射中的任意一个参数固定,另一个参数对C的映射都是线性的。
即双线性的函数有两个输入,而且对这两个输入分别满足线性。
例如矩阵乘法,数据库两张表的笛卡尔积都是双线性配对的例子。
配对函数满足:
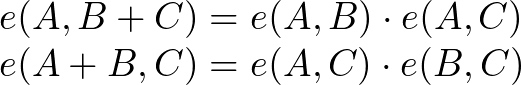
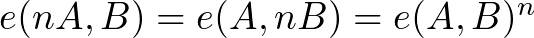
密码学中双线性映射
密码学中的配对用法: 有三个素数p阶群乘法循环群$G_1 \cdot G_2 ,G_T$,三个群存在一个映射关系(函数)$e:G_1 * G_2 \to G_T$,且满足以下性质:
双线性(Bilinearity):对于任意的$g_1 \in G_1 ,g_2 \in G_2$,均有$e(g^a_1,g^b_2)=e(g_1,g_2)^{ab}$成立;
非退化性(Non-degeneracy):$\exists g_1 \in G_1,g_2 \in G_2 $使得 $e(g_1,g2) \not= 1{G_T}$($G_T$单位元)。非退化性保证了只要我们选择椭圆曲线上的非单位成员G,就能得到目标群中的非单位元
可计算性(Computability):存在有效的算法,对于$\forall g_1 \in G_1,g_2 \in G_2$,可计算$e(g_1,g_2)$,显而易见只有这样才具有可实用性。
特殊情况下$G_1=G_2$则称该双线性配对是对称的,否则是非对称的。另外还存在一种合数阶的双线性配对,不再详述!
关于双线性映射可以通过有限域上的超椭圆曲线上的Tate对或Weil对来构造。基于pairing密码学实现库可参考PBC (Pairing-Based Cryptography) library:https://crypto.stanford.edu/pbc/ 当然也有其他库可用,不再列举。
小结
双线性配对特性不仅可以用于签名构造,密钥协商等,还可以实现乘法的同态隐藏和校验。这一点在零知识证明项目中应用很多。
另外需要说明的是,并非基于任何椭圆曲线都可以构造配对函数,对于能有效实现双线性对的椭圆曲线,称为pairing-friendly curves,例如BLS12_381曲线。
关于配对的具体实现如Kate配对实现,涉及背景知识众多,且是高等数学内容,单独说起来晦涩不易理解,好在现在都有成熟的实现库,以后有机会再讲讲配对实例的具体实现吧。
配对也不是完美的, 配对实现需要对曲线做慎重选择,加之操作复杂,运算效率有所降低,例如BLS签名验证效率就比传统的ECDSA要低,配对算法的研究就是在致力改善这一点。
关于配对,还感兴趣的可以参考:
Pairings For Beginners: http://www.craigcostello.com.au/pairings/PairingsForBeginners.pdf
Short signatures from the Weil pairing: https://www.iacr.org/archive/asiacrypt2001/22480516.pdf
既然说到了配对在零知识证明中的应用,从下一节开始,我们开启零知识证明系列! 纵观区块链技术近几年的发展,密码学在区块链领域的创新应用成为区块链创新的基石与引擎,例如以太坊扩容方案zk-rollup等等。
欢迎关注公众号:blocksight
相关阅读:
区块链中的数学 - BLS门限签名 BLS m of n门限签名
区块链中的数学 - BLS密钥聚合 BLS密钥聚合
区块链中的数学 - BLS数字签名 BLS签名及验证
区块链中的数学 - 参与者 < 门限值t的密钥更新Amir Herzberg方案 Amir Herzberg改进方案
区块链中的数学 - Feldman的可验证的密钥分享 Feldman可验证密钥分享方案
区块链中的数学 - Ed25519签名 Ed25519签名
区块链中的数学-ElGamal算法 ElGamal算法签名及验证&实例演练
区块链中的数学-VRF基于ECC公钥体制的证明验证过程 基于椭圆曲线的VRF证明验证过程
Schorr签名与椭圆曲线 Schorr签名与椭圆曲线
区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析(中)
- BLS 签名的微妙之处 164 浏览
- 配对密码学之美:聚合签名和阈值签名 475 浏览
- 配对密码之美:聚合签名和阈值签名 761 浏览
- Shamir份额的魔力:BLS门限签名 587 浏览
- 以太坊、ICP 的 BLS 签名趣谈 1701 浏览
- 什么是BLS签名以及它们如何工作? 2568 浏览
- Alpenglow:快速最终确认性,更公平的经济模型 1520 浏览
- 阈值组签名、分布式密钥生成DKG、BLS签名 2260 浏览
- 引介 Constantine - 用于证明系统和区块链协议的高性能密码学开源库 2978 浏览
- BLS签名、BLS12-381椭圆曲线以及基于配对签名方案的剖析 2805 浏览
- Sequencer 选择加入、发现与通信 849 浏览
- Cobo 密码知识讲堂|第五讲:探索聚合签名奥妙 1380 浏览

