单位根的平方根
- RareSkills
- 发布于 2025-11-12 20:51
- 阅读 2157
本文介绍了在指数形式下求平方根的方法,特别是在单位根上的应用。文章解释了只有偶数次幂的单位根才能开平方,并展示了如何通过开平方操作将k次单位根转化为2k次单位根,同时提供了相关的示例和练习题。
一个数字 的平方根 是指满足 的数。当 的形式为 且 为偶数时,平方根很容易计算:它就是 。这遵循指数的幂法则:
如果我们限制指数为整数,那么 有平方根当且仅当 是偶数。因此, 是 的平方根。
平方根有两个解。例如,4 的整数平方根是 2 和 -2。因此,我们也知道如果 是 的平方根,那么 也是一个平方根。我们可以用代数方法验证这一点:
用指数形式计算数字的平方根的例子
例子 1: 的平方根是什么?
指数是偶数,所以我们可以把指数除以 2。答案是 和 。
例子 2: 的平方根是什么?
因为 被乘以 8,所以 是否为偶数并不重要,因为乘积将是偶数,所以我们知道指数可以除以 2。 的一半是 ,所以答案是 和
例子 3: 的平方根是什么?
同样,我们不需要知道 或 。指数保证是偶数,因为乘以了 2。将指数除以 2,我们得到 ,所以平方根是 和 。
平方根的指数规则
值 有平方根 和 。平方根的指数将是整数,当且仅当 是偶数。
将平方根的指数规则应用于单位根
正如我们已经多次看到的,单位根被写成一个本原单位根的幂。 这是 8 次单位根的乘法子群:
回顾恒等式 。
因为在我们的例子中 ,所以 和 相差 。因此,我们也可以把 8 次单位根写成:
基于平方根的指数规则,只有 omega 的偶数次幂有平方根(在这种情况下,我们认为 0 是偶数):
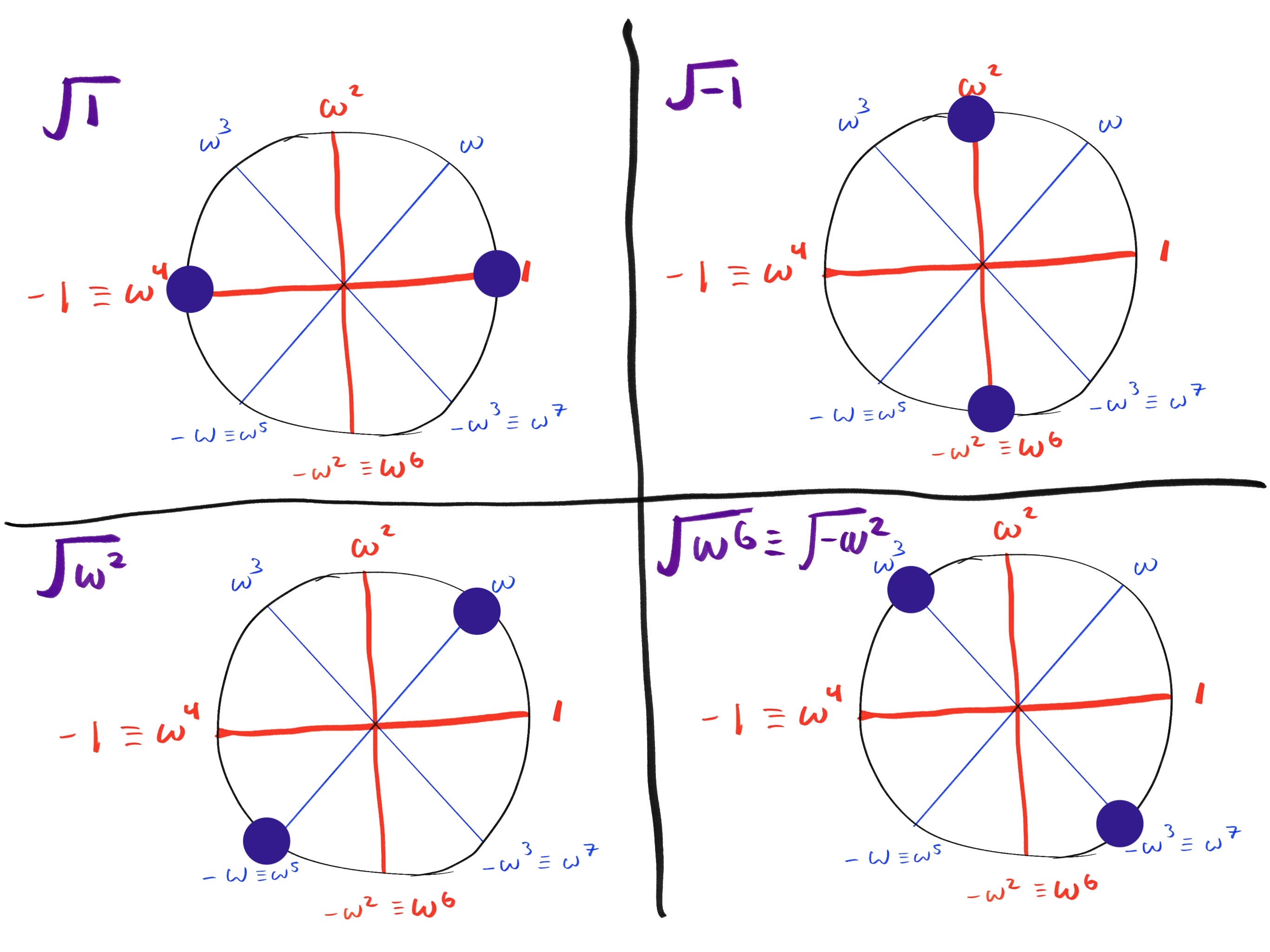
我们可以如下计算它们的平方根:
- 或等价于 和
- 或等价于 和
- 或等价于 和
- 或等价于 和
如果我们将 8 次单位根可视化在圆上,我们注意到只有红色子群的成员(偶数次幂,或等价于 的幂)有平方根:
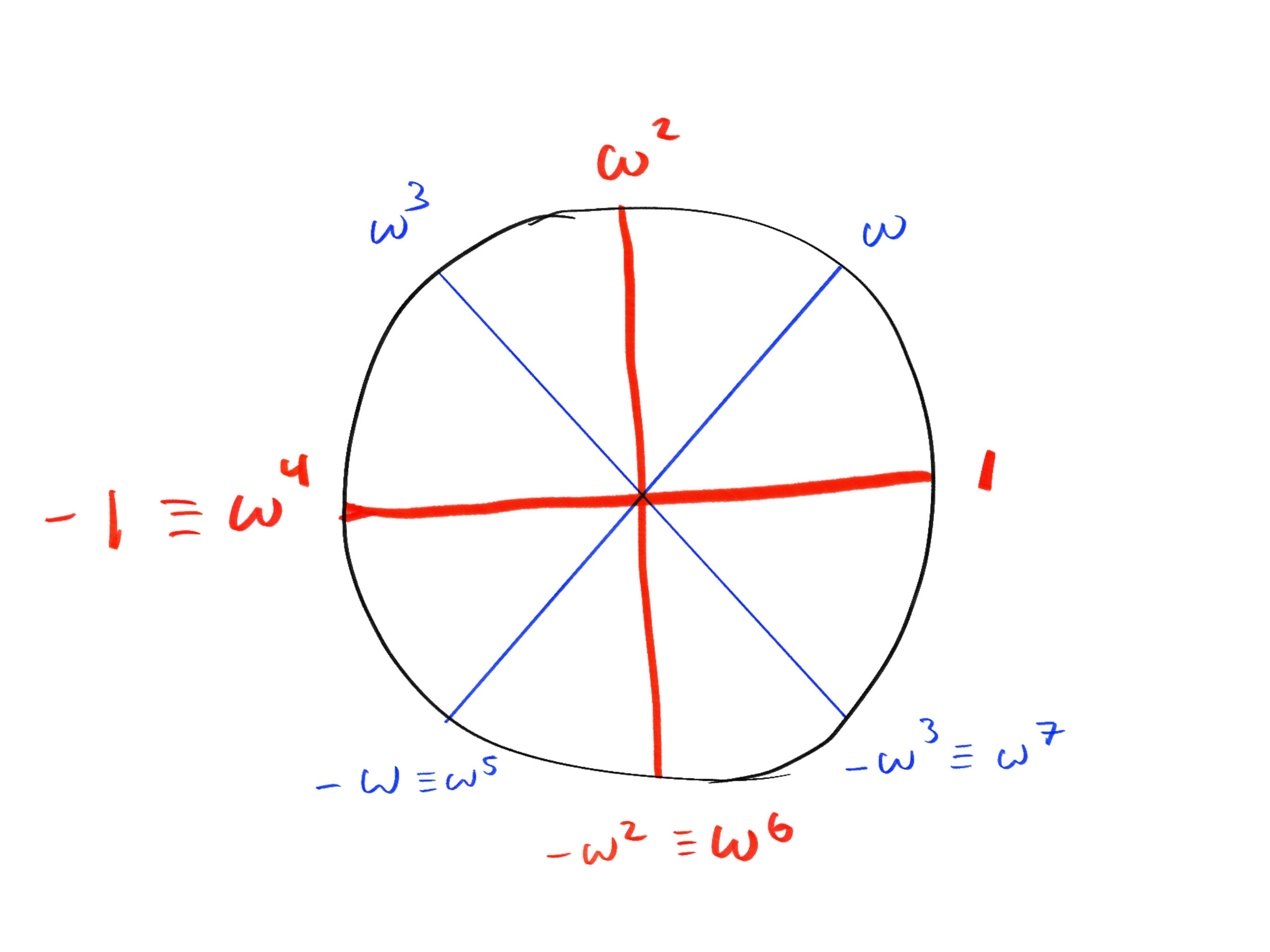
下图显示了每个平方根计算如何产生圆上的两个对立点:
取 k 次单位根的平方根会产生 2k 次单位根 (如果它们存在)
在前面的一章中,我们看到对单位根求平方会使集合的大小减半(假设集合的大小是偶数)。取单位根的平方根会使集合的大小加倍。 例如,考虑由 生成的 8 次单位根,如上所示:
如果我们对每个元素求平方,我们得到集合:
现在,如果我们取这个新集合中每个元素的平方根,我们会得到原始的 8 次单位根,如上节所示:
- 或等价于 和
- 或等价于 和
- 或等价于 和
- 或等价于 和
这不是一个深刻的观察:平方和平方根是相反的运算,所以自然地,平方根应该“撤销”平方所做的事情,反之亦然。
然而,这确实开启了一个优化,我们稍后将利用它。可以重复地对单位根进行平方以缩小集合,执行一些操作,然后使用平方根将结果“提升”回原始集合。我们将在接下来的章节中介绍这些机制,但现在,读者必须完全掌握以下概念:
对 -th 单位根进行平方会将集合减少到 -th 单位根。 取 -th 单位根的平方根会产生 -th 单位根并使集合大小加倍。
总结
- 只有单位根的偶数次幂才有平方根
- 的平方根是 和
- 根据前面的一章,我们知道
- 在圆上可视化平方根。由于平方根总是彼此的加法逆元,因此单位根的平方根位于圆的“相对两侧”。
练习题
- 设 为本原 4 次单位根。 的平方根是什么?
- 设 为本原 32 次单位根。 的平方根是什么?
- 设 为本原 16 次单位根。 的平方根是什么?
- 原文链接: rareskills.io/post/roots...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- FFT友好的有限域 992 浏览
- 单位根的可视化表示 2245 浏览
- k次单位根的平方是k/2次单位根 2089 浏览
- 多值函数的图像保持定理 2081 浏览
- 单位根的 k/2 次幂等于 1 或 -1 2077 浏览
- 手动实现数论变换算法 2058 浏览
- 使用平方根展开评估多值函数 2010 浏览
- 有限域中的单位根 1981 浏览
- ZK数学101:椭圆曲线离散对数问题 1430 浏览
- 零知识证明中的循环群 2051 浏览
- 一个密文,多个消息:FHE中的SIMD操作 2168 浏览

