零知识证明 - zkEVM源代码分析(MPT Circuit)
- Star Li
- 发布于 2022-05-26 09:03
- 阅读 5106
文章分为两部分:1/介绍MPT的基础背景知识 2/导读MPT电路代码和原理。
前两篇文章重点介绍了zkEVM的zkEVM电路和State电路:
零知识证明 - zkEVM源代码分析(EVM Circuit)
零知识证明 - zkEVM源代码分析(State Circuit)
接着分析zkEVM的另外一个大的模块:MPT Circuit。这篇文章主要是对zkEVM mpt spec以及相关代码的导读与总结:
https://github.com/appliedzkp/zkevm-specs/blob/mpt/specs/mpt-proof.md
文章分为两部分:1/介绍MPT的基础背景知识 2/导读MPT电路代码和原理。
1 预备知识
1.1 ETH区块结构
ETH的一个区块中包括了 3 棵树(MPT),分别是 state Trie,tx Trie,receipt Trie。
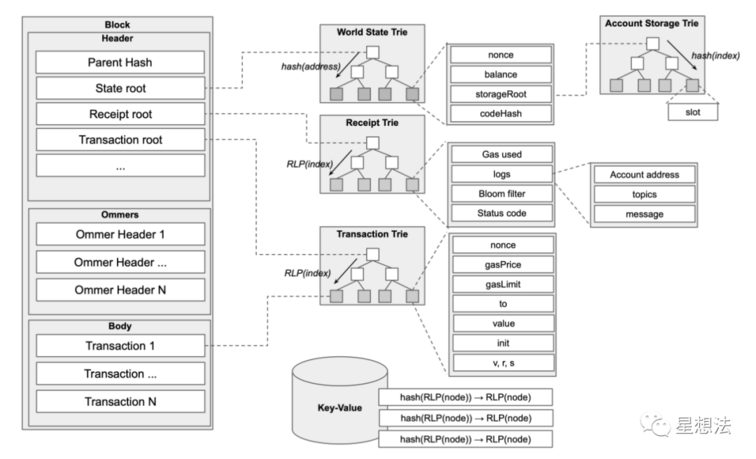
(https://arxiv.org/pdf/2108.05513.pdf)
从上图可以看到,区块头中存储了三棵树的树根。其中我们最关注的是 state Trie。
ETH Account的定义是:
Account {
Nonce,
Balance,
CodeHash,
StorageRoot,
}同时,ETH有两种账户:
- EOA(External-Owned-Account):普通账户。EOA有 Noce,Balance,但是它的 CodeHash,StorageRoot则为空。
- Contract Account:合约账户。除了普通账户的功能外,账户记录合约代码。值得注意的是,合约代码并不存储在 MPT 树上,而是在相应的数据结构(stateObject)中有一个字段来记录合约的 bytecode,这段 bytecode 的 hash 将记录在 Account 中的 CodeHash 字段。所以,合约账户拥有 CodeHash,StorageRoot 两个字段。
1.2 RLP 编码
wiki上对RLP编码有比较详细的解释。
https://eth.wiki/fundamentals/rlp
1.2.1 RLP 编码的目标
RLP 编码以下两种内容:
- A string (ie. byte array) is an item
- A list of items is an item
1.2.2 RLP 编码规则
- For a single byte whose value is in the [0x00, 0x7f] range, that byte is its own RLP encoding.
- Otherwise, if a string is 0-55 bytes long, the RLP encoding consists of a single byte with value 0x80 plus the length of the string followed by the string. The range of the first byte is thus [0x80, 0xb7].
- If a string is more than 55 bytes long, the RLP encoding consists of a single byte with value 0xb7 plus the length in bytes of the length of the string in binary form, followed by the length of the string, followed by the string. For example, a length-1024 string would be encoded as \xb9\x04\x00 followed by the string. The range of the first byte is thus [0xb8, 0xbf].
- If the total payload of a list (i.e. the combined length of all its items being RLP encoded) is 0-55 bytes long, the RLP encoding consists of a single byte with value 0xc0 plus the length of the list followed by the concatenation of the RLP encodings of the items. The range of the first byte is thus [0xc0, 0xf7].
- If the total payload of a list is more than 55 bytes long, the RLP encoding consists of a single byte with value 0xf7 plus the length in bytes of the length of the payload in binary form, followed by the length of the payload, followed by the concatenation of the RLP encodings of the items. The range of the first byte is thus [0xf8, 0xff].
总结一下:
- 前三条针对单个 string 编码,而后两条针对 list 编码
- 编码的基本组成是 prefix + content
- prefix = fixed_prefix + content_length。
- fixed_prefix 依据编码内容长度不同而有所不同。
1.2.3 RLP 例子
The string “dog” = [ 0x83, ‘d’, ‘o’, ‘g’ ]
The list [ “cat”, “dog” ] = [ 0xc8, 0x83, 'c', 'a', 't', 0x83, 'd', 'o', 'g' ]
The empty string (‘null’) = [ 0x80 ]
The empty list = [ 0xc0 ]
The integer 0 = [ 0x80 ]
The encoded integer 0 (’\x00’) = [ 0x00 ]
The encoded integer 15 (’\x0f’) = [ 0x0f ]
The encoded integer 1024 (’\x04\x00’) = [ 0x82, 0x04, 0x00 ]
The set theoretical representation of three, [ [], [[]], [ [], [[]] ] ] = [ 0xc7, 0xc0, 0xc1, 0xc0, 0xc3, 0xc0, 0xc1, 0xc0 ]1.3 Compact 编码
Compact编码以及MPT的信息同样引用wiki的文章:
https://eth.wiki/fundamentals/patricia-tree
1.3.1 Compact 编码内容
- 拆分成 nibbles 的 hex sequence。所谓的 nibble 就是 4 bits 的一个十六进制数(也就是说,它的值是 0 - f)。
- 该 hex sequence 可以有也可以没有截止符(Optional terminator)。截止符是 0x10。
1.3.2 Compact 编码规则及示例
> [ 1, 2, 3, 4, 5, ...]
'11 23 45'- 没有截止符,且待编码长度为奇数
- 所以在头部添加 1,然后两个 nibbles 一组
> [ 0, 1, 2, 3, 4, 5, ...]
'00 01 23 45'- 没有截止符,且待编码长度为偶数
- 所以在头部添加 00,然后两个 nibbles 一组
> [ 0, f, 1, c, b, 8, 10]
'20 0f 1c b8'- 有截止符,且除去截止符外(截止符不参与编码),待编码长度为偶数
- 所以在头部添加 20,然后两个 nibbles 一组
> [ f, 1, c, b, 8, 10]
'3f 1c b8'- 有截止符,且除去截止符外(截止符不参与编码),待编码长度为奇数
- 所以在头部添加 3,然后两个 nibbles 一组
总结:
- 根据是否有截止符,有两组不同的 prefix,没有截止符 (0,1),有截止符 (2,3)。
- 添加 prefix 后要使得算上 prefix 后的总长度为偶数(以使得能够两两一组完成编码),因此有时要再添加 0 来调节。
1.3.3 Compact 编码在 MPT 中的应用
- 编码的位置是 leaf node(带截止符),extension node(不带截止符)
- 编码的对象是在本 node 中出现的 path。
hex char bits | node type partial path length
----------------------------------------------------------
0 0000 | extension even
1 0001 | extension odd
2 0010 | terminating (leaf) even
3 0011 | terminating (leaf) odd1.4. Merkle Patricia Trie (MPT)
ETH 用来存储状态的是一棵字典树,其存储的内容是(key,value),而 key 就体现为树的 path。
1.4.1 Patricia Trie

由上图,只要把握如下几点即可:
- 四种类型的 node
- NULL (represented as the empty string)
- Branch Node: A 17-item node [ v0 ... v15, vt ]
- Leaf Node: A 2-item node [ encodedPath, value ]
- Extension Node: A 2-item node [ encodedPath, key ]
- 在 branch node 的 nibble 中与 extension node 的 next node 中存储的是 下级节点的 hash 值。(When one node is referenced inside another node, what is included is H(rlp.encode(x)), where H(x) = sha3(x) if len(x) >= 32 else x and rlp.encode is the RLP encoding function)。
1.4.2 State Trie & Storage Trie
State Trie 的信息是:
- key = sha3(eth_address)
- value = rlp(eth_account)
Storage Trie 的信息是:
- key = sha3(contract_var_position)
- value = rlp(contract_var_value)
有关MPT内存以及存储的数据结构也可以看看很早之前写的文章:
2 MPT Circuit
本节是 ZKEVM MPT SPEC 及相关代码的一个导读和综述。
2.1 MPT 要证明什么
MPT circuit的目的是:
MPT circuit checks that the modification of the trie state happened correctly.
欲达成此目的,采取的原则是 每次只处理一个值变化所引起的 state root 的变化。这就是原文如下说明的意思:
The circuit checks the transition from val1 to val2 at key1 that led to the change of trie root from root1 to root2 (the chaining of such proofs is yet to be added)
于是问题进一步归约为证明两条 path 的正确性,即: path1: (key1, val1) -> root1,path2: (key1, val2) -> root2。而所谓证明 path 的正确性,就是证明在这条路径上的 所有下级节点的 hash 出现在上级节点的正确位置上。
基于此,需要处理如下几个问题:
- 如何完整表示一条路径的信息
- 如何表示 former state 和 latter state
- 如何表示 MPT 中的 Branch,Extension,Leaf
- 如何验证 Hash 的正确性
- 如何证明 Hash 出现在正确的位置
- 如何证明 key(即:address/position) 的正确性
2.2 完整路径及前后状态的表示
2.2.1 完整路径的表示
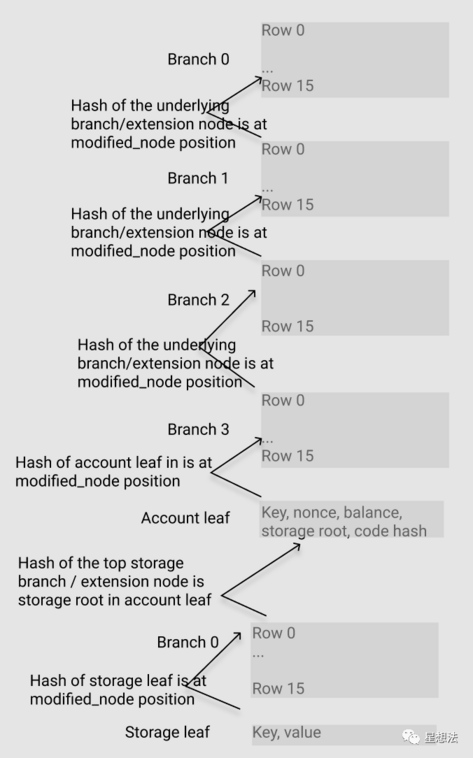
由上图可知,电路的排布与真实的 path 是完全一致的。有如下三部分:
- storage leaf
- branch node(包括extension node)
- account leaf
图中的折线箭头代表了下级节点的 Hash 应该在上级节点的正确位置出现,同时代表了欲证明的该命题。该折线箭头的含义在 spec 中反复用到。
2.2.2 前后状态的表示
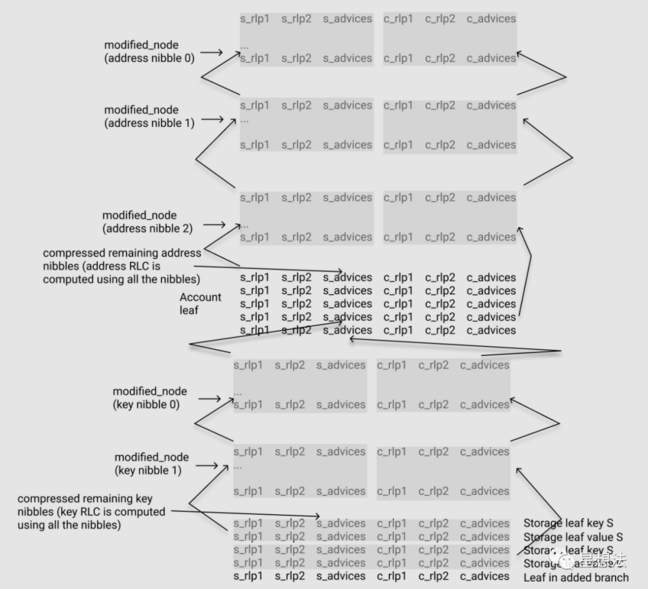
由上图可知:
- 有 S, C 两个 path proof 并列摆放。其中 S 代表 former state,C 代表 latter state。
2.2.3 MPT Proof Overview

上图很详细地阐述了 MPT Circuit 的功能。就是证明了两条 MPT Path。
2.3. Branch/Extension Node 的表示及关系
2.3.1. Branch Node 的表示
Branch/Extension Node 在电路中可以视为一个 block,可以很清楚地表示为:
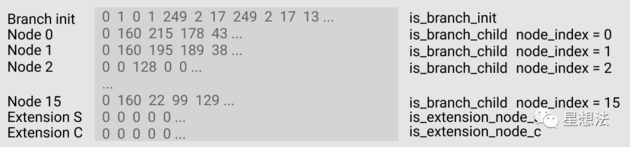
- 在电路中属于同一个功能块
- 该功能块一共有 19 行,它们是:
- 第一行 branch init
- 接下来的 16 行,每一行代表一个 nibble (0 ~ f)。
- 最后两行代表两个 extension node 的信息。
- 该块一共有 34 列,它们是:
- 第一列代表出去本行 rlp 编码后所剩余的 rlp 长度
- 第二列代表 rlp 编码的 prefix。
- 后 32 列代表 Hash 的 32 个字节,每一列存储一个字节(注意目前是小端表示)。
- branch init 行存放了该 branch node 的相关信息,比如 RLP 编码信息,相关的选择子信息。
2.3.2. Extension Node 的表示

虽然是同一个功能块 block,但是实际上表示 extension node 是最后两行。而且,这两行是横跨 S,C 两大块的。这两行的具体含义是:
- S 行的 S 块(s_rlp1,s_rlp2,s_advices)代表了该 extension node 的 key (key本身自然是 compact 编码,同时其存储时还要进行 rlp 编码序列化)。
- S 行的 C 块,则代表了 extension node S (即 former ext node)的值(也就是下级节点的 hash)的 rlp 编码。
- C 行的 S 块,代表了 extension node key 的一部分,作用是为了让解码更加方便。这里不存储完整 key 的原因是,former ext node (S) 与 latter ext node (C) 有相同的 key。
- C 行的 C 块,代表了 extension node C (即 latter ext node)的值(也就是下级节点的 hash)的 rlp 编码。
2.3.2. Branch/Extension Node 的关系
- 对 branch node 来说,即:如果上面的 block 代表了branch node,那么它的最后两行,即 extension S/C 都是代表空
- 对 extension node 来说,只要掌握其 block 中代表 branch node 那些行具体含义即可。简单说,此时,这些行不为空,而是代表了该 extension node 的下级 branch node。具体如下图所示:

掌握了这一点,也就能明白上图的含义。也就是,extension node 的 hash 在上一个 block 中,而本 block 中的 branch node 的 hash 在该 extension node 中存储。
2.4. Leaf 的表示
有 Account leaf 和 Storage leaf 两种叶子节点,二者都用 5 行来表示,只不过二者的具体含义不同。
2.4.1 Account Leaf 的表示
Key S \
Nonce balance S \
Nonce balance C \
Storage codehash S \
Storage codehash C
这里要注意如下两点:
- 对同一个账户来说它们前后两个状态的地址都是一样的,所以 key 只用一行来表示
- 这五行也是横跨了 S,C 两大部分。
2.4.2. Storage Leaf 的表示
Leaf key S \
Leaf value S \
Leaf key C \
Leaf value C \
Leaf in added branch
具体如下图所示,该图修改了一处原图的小错误:
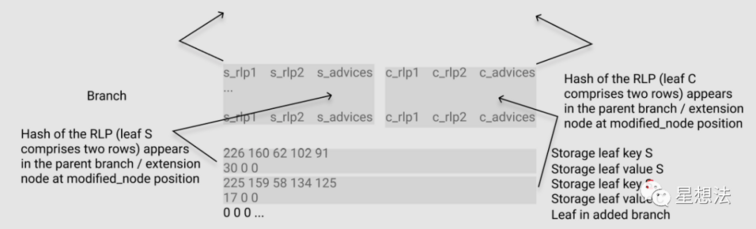
这里也注意以下两点:
- Key S,C 是有可能不同的,比如插入或者删除节点的时候
- 各行仍然是横跨 S,C 两大部分
2.5. 证明 Hash 及其位置的正确性
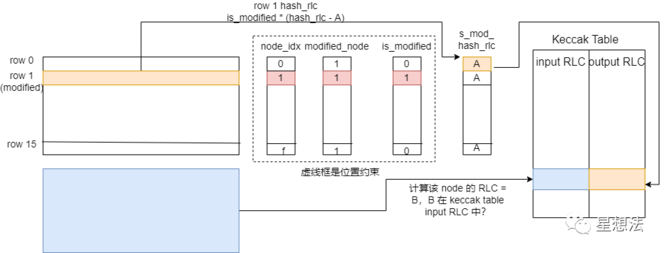
- mode_index,modified_node,is_modified三列用来限制相关位置的正确性
- is_modified,s/c_mod_hash_rlc,用来约束 path 上 hash_rlc 的正确性。其中如图所示,s/c_mod_hash_rlc 在某一个节点处的值都是一样的,这样做的目的是写约束方便。就上图来讲就要求 row 1 的存储的 hash 求得的 hash_rlc 与 A 是相等的。
- keccak table 保证了 hash 计算的正确性。
- 下级节点的 rlc 应该在 keccak table 的 input 列。
- A 应该在 keccak table 对应的输出列。
通过以上的约束,就证明了下级节点 hash 计算的正确性,以及下级节点的 hash 出现在了上级节点正确的位置上。
2.6. 与 Hash 相关的 RLC 的计算
本节主要介绍与 hash 相关的 rlc 的计算。具体可以分为 branch node,extension node,account leaf 和 storage leaf 的 rlc 的计算。spec 中的一大部分就是在介绍该部分的计算,已经很详细,这里只对其中的要点和某些较难理解的地方做一个阐述。
2.6.1. Branch node RLC
Branch node RLC 从计算上来说分为两部分,一部分是存储在 branch init 行中该 branch rlp 编码信息的 rlc,第二部分是该 branch node 各行的 rlc。
branch init rlp 编码 rlc 的计算如下图
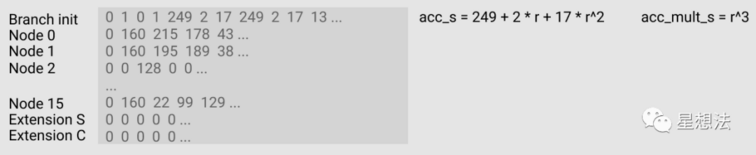
这里只需要注意,相关 rlp 编码在 branch init 行的位置即可:
- 列 4,5,6 为 branch node S (在代码中就是 s_advices[2 - 4])的 rlp meta,列 7,8,9 为 branch node C (代码中体现为 s_advices[5 - 7])的 rlp meta。之所以用三列来表示,是与该节点待编码的数据长度有关,如果较长,如图例,则用三个字节;如果较短,比如该节点很多为空,则用两个字节。
- 区分长度表示(两个字节还是三个字节)的标志就是 branch init 行中最开始的四个位置。列 0,1 (代码中就是 s_rlp1,s_rlp2)为 S rlp 需要的字节长度;列 2,3(代码中是 s_advices[0],s_advices[1])代表 C rlp 需要的字节长度。
- (1,0)表示两个字节,(0,1)表示三个字节。
- 可以看到 acc_s 列,该列代表了 rlc 的结果,acc_mult_s 列,该列代表了在当前行起始的随机数(r的幂次)。
branch node rlc 的计算如下图所示:

对 branch node rlc 的计算只需要牢记一点,就是 s/c_rlp1 不参与计算,换句话说,每一行的计算是从 s/c_rlp2 开始的。
最后需要说明的是,在计算 branch node rlc 的时候,还要对 init 行中所记录的长度是否正确进行检查,具体的检查过程如下图所示:

这里需要注意的是:
- 如上文所述,总长度记录在 init 行中
- branch node 中 row 0 - row 15 的 rlp1 均记录了除掉该行长度后所剩余的长度。所以约束就是 s/c_rlp1_pre = s/c_rlp1_cur + cur_row_len
- 在 row 15 要求剩余的长度应该不等于0(目前要求等于1),这是因为还有 value 的值可能接在后面。
2.6.2. Extension node/Account leaf RLC
这部分就很简单,就是将相应行的值依次算过去,算一个 rlc 出来,因此在 spec 中都没有写,代码中会看到。
2.6.3. Storage leaf RLC
这部分在通常情况下,也就是 key 不发生变化的情况,其计算也是简单的,与 extension node/account leaf rlc 的计算没有什么不同。但是还有几个特殊情况,说白了其实就是增删节点。文档也处在不断变化中,这里就目前情况结合代码做个总结。
case 1: Leaf turns into branch / extension node
Branch 0 | Branch 0
| Branch 1
Leaf 1 | Leaf 2处理这种情况,只要掌握以下几个要点,即可理解:
- 该情况是因为 Leaf 2 的插入,而导致了 Leaf 1 的层级发生了变化。值得注意的是,并不是 Leaf 1 本身的变化而引发了这种情况。
- 所以 spec 说现在 Branch 1 有两个叶子:Leaf 1 和 Leaf 2。只不过新的 Leaf 1 在上图中没有体现出来,我们可以用 Leaf 11 来表示在 Branch 1 下的 Leaf 1。所以 Leaf 1 与 Leaf 11 是一模一样的,只不过由于层级变化,Leaf 11 中的 key 更短而已。
- Leaf 11 就存储在 storage leaf 的第五行,也就是 Leaf in addition branch 中。在 spec 中,Leaf 1 就 “drifted”(漂移) 到了 Leaf 11 处。
- 随着 Leaf 1 的漂移,除了 Leaf 2 的 hash 要出现在 Branch 1 的 modified_node 处之外,Leaf 11 的 hash 同时要出现在 Branch 1 的 drifted_mod 处。
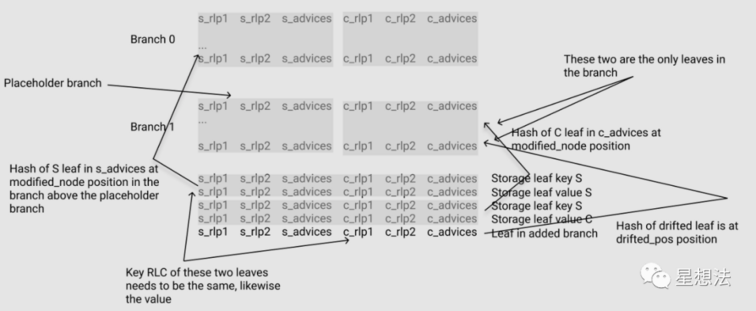
由上图就可以看到基本的约束:
- Leaf 1 的 hash 要在 S Branch 0 中 modified_node
- Leaf 2 的 hash 要在 C Branch 1 中 modified_node
- Leaf 11 的 hash 要在 C Branch 1 中 drifted_mod(pos)
- Leaf 1 与 Leaf 11 的 key 和 val 要一致
这里为了保持原有 branch block 的平衡,于是引入了 placeholder branch 的概念,也就是上图中 S branch 1。这里需要掌握如下几个要点:
- placeholder 是一个占位符。同时这个占位符与其并肩的另一个 branch node (就是文档中所谓 counterpart)长得一模一样;具体来说,如果 S 是 placeholder,那么它长得与并肩的 C branch node 一模一样,反之亦然。
- 这样做的好处是依然能够保持普通 S branch node 与 C branch node 的约束,即:在非 modified_node 处二者一样。(branch.rs)
- 更特殊的是,在非 modified_node,非 drified_pos 的行,应该都是空行。(branch.rs)
- 从代码中看,对于 added branch(Leaf 11)hash 应当出现在 C branch 1 的 drifted_pos 处,并没有直接的约束。其真实约束的是,Leaf 11 的 hash 出现在了 placeholder 中。(leaf_key_in_added_branch.rs)
掌握了以上解析,也就能相应处理删除节点的情况了。
case 2: Key not used yet
Branch 1 | Branch 1
| Leaf 2对此种情况的处理,也运用了 placeholder 的方法,只不过这次 placeholder 出现在了 leaf 上。
Branch 1 | Branch 1
Leaf 1 | Leaf 2注意在 spec 中没有提及对 placeholder leaf 的 witness 的处理,在代码中目前看到的是要求全部填 0(leaf_value.rs)。

这里比较有特点的地方是,placeholder leaf 在 上级节点的对应位置处的 hash 应该为空。
有了以上理解,就能理解 spec 中 case 3 与 case 4,它们就是 case 1 与 case 2 发生在第一级的情况。
2.7. Key RLC 的计算
Key RLC 的计算是为了证明 address 与 position 的正确性,对于一条完整的 path 来说,它有 branch node,extension node 和 leaf 三种,下面分别介绍。
总体来说,
- address 和 position 都是 key,都是 32 bytes,64 nibbles
n0n1, n2n3, ..., n62n63- 所以 key 的 rlc 的计算方式为
key_rlc = (n0 * 16 + n1) + (n2 * 16 + n3) * r + (n4 * 16 + n5) * r^2 + ... + (n62 * 16 + n63) * r^31- 而分三种情况讨论,是因为构成 key 的 nibble 是分散在三种节点中的,讨论的终极目的是正确找到即将面对的 nibble 的位置。
- 带来这种复杂性的原因是 Compact 编码,以及 nibbles 是分散在三种节点中的。
2.7.1. Branch node key RLC
Branch node key rlc 的计算最为简单直接,因为在 mpt proof 场景下,每个 branch node 只有一个 nibble (也就是 branch node 中的某一行)参与计算,所需区分的不过是该 nibble 是 C16 还是 C1,这是由 branch init 行中的选择子决定。
具体过程如下图:

2.7.2. Extension node key RLC
Extension node key rlc 的计算根本原理一样,只是由于
- extension node 承上启下,处于 path 中间(区别于 leaf node)
- extension node 可能存储了多个 nibble(区别于 branch node)
- key 的 compact 编码方式的存在
- 整个 node 的 rlp 编码方式的存在(只有一个 nibble 的情况)
所以,extension node key rlc 的计算所需讨论的情况最多,这也就是 spec 花费很多笔墨的地方。但其实很简单,下面直接拿 spec 的例子说明。
如果 extension node 中存储的 nibble 是偶数,例:
[228,130,0,149,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]注意这里前两个是 rlp 编码,可不管。真正有用的是 0,149 两个字节,其十六进制表示为 00,95。按照 compact 编码规则,这代表了本 extension node 存储的 key 的长度为偶数(该例为2),其值为 95。这里需要牢记的是,这只代表了本行的情况,这里需要讨论的就是 9,5 在 key 中到底应该是 C16 还是 C1。
- 如果 extension node 之前 nibble 个数为偶数。这说明,95 就是 key 中的一个字节,可以直接参与计算,只需找到正确的 r 的次幂即可。其计算是:
key_rlc = key_rlc_prev + 149 * key_rlc_mult- 如果 extension node 之前 nibble 个数为奇数。这说明,9 其实是 key 中上一个字节的低位,而 5 是 key 中下一个字节的高位。所以其计算是:
key_rlc = key_rlc_prev + 9 * key_rlc_mult + 5 * 16 * key_rlc_mult * r如果 extension node 中存储的 nibble 是奇数,例:
[228,130,19,149,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]该例 19,149 的十六进制表示为 13,95,这说明该 extension node 的 nibble 长度为奇数,而所包含的 key 的 nibble 为 3,9,5。以下讨论的核心仍然是谁是 C16 谁是 C1 的问题。
- extension node 之上 nibble 个数为偶数。则 3 是高位,9 是低位,5 是高位。计算为:
key_rlc = key_rlc_prev + ((19 - 16) * 16 + 9) * key_rlc_mult + 5 * 16 * key_rlc_mult * r- extension node 之上 nibble 个数为奇数。则 3 为低位,95 是一个完整字节。计算为:
key_rlc = key_rlc_prev + (19 -16) * key_rlc_mult + 149 * key_rlc_mult * r最后一种情况是 extension node 中只有一个 nibble。这时,rlp 编码的方式又发生了变化,也就是没有了代表长度的字节(就是上例中的 130)。例:
226,16,160,172,105,12...此时,该 extension node 中所存储的 nibble 就是 0。而具体的计算也与上文一样,跟 extension node 前 nibble 的个数是奇数还是偶数有关。具体公式可参看文档或者自行推导。
以上就讨论清楚了 extension node 的 key rlc 的计算。具体控制以上情况的就是一些 spec 中提到的选择子。
2.7.3. Leaf Key RLC 计算
有了上文的铺垫,leaf key rlc 的计算就显得很容易了。由于 leaf node 已经没有下级节点了,因此它的情况要简单得多,因为其本身存储的 nibble 如果为偶数,那么 leaf 之前的 nibble 个数就一定是奇数;本身 nibble 如果是奇数,那么 leaf 之前的 nibble 就一定是偶数。而这两种情况 key rlc 的计算已经在 extension node key rlc 计算中讨论过了。
而判断 leaf 中 nibble 的个数又由 leaf key 的 rlp 编码决定,主要是长度大于 55 还是小于等于 55,这里也不赘述了。
2.7.4. 对 key 正确性的判断
这里很简单,没有用 lookup,代码中只用了一条简单的相等约束。(leaf_key.rs)
3. MPT电路资源
截至目前,整个 mpt 电路较大,相关资源的消耗为:
advice column: 108
fixed column: 7
instance column: 1
custom gates: 42
到目前为止,zkEVM比较大的核心模块都分析完了。zkEVM是非常有意义的zk应用,也是目前电路规模最大,最复杂的zk系统。感兴趣的小伙伴可以一起深入研究。
- ZK编年史:哈希登场 84 浏览
- 以太坊协议研究学习小组 - 2026 启动 169 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 312 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 265 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 336 浏览
- Zcash:比特币遗忘的隐私 412 浏览
- ZK编年史:计算模型 285 浏览
- lambdaworks 2026 年更新路线图和优先级 340 浏览
- 2026年构建机构级DeFi平台真正需要什么 846 浏览
- zkMesh:2026年1月回顾 434 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 615 浏览
- Zcash 的时代到来了 733 浏览

