Vitalik: zk-SNARK 何以可能 —— 引介杀手锏“多项式承诺”

来源 | vitalik.ca

作者 | Vitalik Buterin

翻译 | 双花 (@doublespending)

校对 | ECN

编者注：说到过去十年来诞生的最强密码学技术，肯定免不了提及零知识证明 (zero knowledge proof)。在区块链领域中，它们有两大应用场景：可扩展性和隐私。zk-SNARK 作为其中一种 zkp 技术，在近几年来也得到了较大的突破，以太坊上出现了诸如 zkSync、Scroll、Hermez 等此类使用 zk-SNARK 证明的通用扩容解决方案。

然而，实现 zk-SNARK 并不简单，因为对某个声明生成了 zk-SNARK 证明之后，验证者需要以某种方式检查计算中的数百万个步骤。多项式承诺就是在这里发挥其作用，即可以将计算编码为多项式，然后使用一种特殊类型的多项式“哈希”(多项式承诺)，以允许验证者在极短的时间内验证多项式等式，即便这些计算背后的多项式规模无比大。

在本文中，Vitalik 介绍了 zk-SNARK 技术的工作原理和难点，然后解释了多项式以及多项式承诺如何让 zk-SNARK 的实现更加高效。

特别感谢 Dankrad Feist、Karl Floersch 以及 Hsiao-wei Wan 的反馈和校对。

过去十年来诞生的最强密码学技术大概要数通用简洁零知识证明，通常称为 zk-SNARK（zero knowledge succinct arguments of knowledge）。zk-SNARK 允许你生成一个证明 (这个证明是针对一些运算得出的特定输出，可用于对该运算的验证)，通过这种方式，即使底层计算十分耗时，该证明也可以被快速验证。“ZK”（零知识）为证明新增了一个额外特性：证明可以隐藏计算的某些输入。

例如，您可以对以下声明生成一个证明：“我知道一个秘密值，如果你将数字添加到挑选的单词 cow 的末尾，然后对其进行 1 亿次 SHA256 哈希运算，那么输出的哈希值以 0x57d00485aa 开头”。验证者验证该证明的耗时可远小于自行进行 1 亿次哈希运算的耗时，而且证明也不会泄漏秘密值。

在区块链领域中，该技术有两大应用场景：

1. 可扩展性：如果一个区块的验证十分耗时，某个人可以验证区块并生成一个证明，而其他人只需快速地验证证明即可

2. 隐私：你可以证明你有权转移某些资产（你收到了该资产，而且你还没有转走），而不透露该资产的来源。这不会对外泄漏交易双方的信息，确保了交易的安全性。

然而，zk-SNARK 是相当复杂的；实际上，就在 2014-17 年，它们还常被称为“月亮数学”。好消息是，从那时起，协议愈发简化，我们对它们的理解也愈发深入。本篇博客将试图以一种数学水平普通的人能理解的方式来解释 ZK-SNARKs 的工作原理。

注意，我们将聚焦于可扩展性；一旦有了可扩展性，这些协议的隐私性就相对容易实现，因此我们将在最后回归这个主题。

为什么 ZK-SNARK “会”很难

以开头例子为例：我们有一个数字（我们可以将末尾跟着秘密输入的 “cow” 整体编码为一个整数），我们计算该数字的 SHA256 哈希，然后重复做 9999999 次，最后我们检查输出的开头。这里面的计算量特别大。

一个“简洁（succinct）”证明指的是证明大小和验证耗时的增长远慢于需验证计算量的增长。如果我们想要一个“简洁”证明，我们就不能要求验证者在每轮哈希中做一些运算（因为那样的话，验证耗时将与计算量成正比）。相反，验证者必须以某种方式检查整个运算过程，而不必窥视运算过程中的每个部分。

有一种自然的技术就是随机抽样：让验证者只在 500 个不同的地方检查运算的正确性，如果所有的 500 个检查都通过了，那么认为运算过程的其余部分也大概率没问题？

该流程甚至可以通过使用 Fiat-Shamir 启发式（Fiat-Shamir heuristic）转化为非交互式证明：证明者计算运算过程的默克尔根，基于默克尔根伪随机地选取 500 个索引，并提供对应的 500 个默克尔分支。核心思想是证明者并不知道将要揭示哪些分支，直到他们已经对数据生成了“承诺”。如果恶意证明者在了解到需要检查哪些索引后试图篡改数据，那么这会改变默克尔根的值，而这将导致一组新随机索引被选出，这将需要再次去篡改数据...让恶意证明者陷入无休止的循环中，无法达成目的。

但不幸的是，简单地随机抽查运算过程存在一个致命的缺陷：运算过程本身并不健壮。如果恶意证明者在计算过程中的某个位置翻转一个比特，可以导致一个完全不同的结果，而随机抽样验证者几乎永远不会发现。

只需一次故意的插入错误，就会导致计算得出完全错误的结果，而这几乎不会被随机检查所捕获。

如果要提出一个 zk-SNARK 协议，那么很多人会走到上面这步，然后陷入困境，最终放弃。不单独查看每个计算片段的情况下，验证者究竟如何才能够校验每个计算片段？事实证明，有一个绝妙的解决方案。

多项式

多项式是一类特殊的代数表达式，具有以下形式：

• $x+5$
• $x^{4}$
• $x^{3} +3x^{2}+3x+1$
• $628x^{271} +318x^{270}+530x^{269}+...+69x+381$

也就是说，它们是有限个形式为 $cx^{k}$ 的项之和。

多项式有许多有趣的特性。但这里，我们将聚焦于多项式的一个特性：多项式是一个可以包含无限信息量（多项式显然可视为一个整数列表）的单一数学对象上。 面的第四个示例包含 tau 的 816 位的信息，而且我们能够很容易地想象出一个包含更多信息量的多项式。

此外，多项式间的单个等式就能够表示无限个数间的方程。 例如，考虑等式 $A(x)+B(x)=C(x)$。如果该等式是正确的，那么下面也是正确的：

• $A(0)+B(0)=C(0)$
• $A(1)+B(1)=C(1)$
• $A(2)+B(2)=C(2)$
• $A(3)+B(3)=C(3)$

可以类推到每个可能的下标。甚至，你可以构造特地表示一组数字的多项式，这样你就可以一次性地检查众多等式。例如，假设您想检查：

• $12 + 1 = 13$
• $10 + 8 = 18$
• $15 + 8 = 23$
• $15 + 13 = 28$

您可以使用一个名为拉格朗日插值的方法来构造多项式：$A(x)$在某些特定下标集合（例如 (0，1，2，3) 上的输出为 (12，10，15，15)），$B(x)$ 在相同下标上的输出为 (1，8，8，13)，如此类推。准确地说，以下是相应的多项式：

• $A(x)=−2x^3+\frac{19}{2} x^2−\frac{19}{2} x+12$
• $B(x)=2x^3-\frac{19}{2} x^2+\frac{29}{2}x+1$
• $C(x)=5x+13$

用这些多项式校验等式 $A(x)+B(x)=C(x)$ 相当于同时校验上述四个等式。

将多项式与自身进行比较

甚至，你可以用一个简单的多项式等式来校验相同多项式的大量相邻取值的关系。这稍微更进一步。假设您想校验，对于给定的多项式$ F$，在整数范围 $\left {0,1…98\right }$内满足$ F(x+2)=F(x)+F(x+1)$（因此，如果您还校验$F(0)=F(1)=1$，那么$ F(100)$ 将是第 100 个斐波拉契数）。

作为多项式，$F(x+2)−F(x+1)−F(x)$ 不会正好为零，因为它在 $x=\left {0,1…98\right }$范围外的取值是不受限的。但我们可以做一些巧妙的处理。一般而言，有这样一条定则：如果多项式 $P$ 在某些集合 $S=\left {x{1}，x{2}…x{n}\right }$上的取值为零，那么可以表示为 $P(x)=Z(x)∗H(x)$ 的形式，其中 $Z(x)=(x−x{1})∗（x−x{2})∗...∗(x−x_{n})$，而且 $H(x)$ 也是一个多项式。换句话说，在某个集合上值为零的任一多项式可以表示为在相同集合上值为零的最简（最低阶）多项式的（多项式）倍数。

为什么会这样？这其实是多项式长除法的一个巧妙的推论：因式定理（the factor theorem）。我们知道，当用 $Z(x)$ 除 $P(x)$ 时，我们将得到商 $Q(x)$ 和余数 $R(x)$，满足 $P(x)=Z(x)*Q(x)+R(x)$，其中余数 $R(x)$的阶严格小于 $Z(x)$。因为我们知道多项式 $P$ 在集合 $ S $ 上的取值为零，这意味着多项式 $R$ 在集合 $S $上的取值也必须为零。因此，我们可以通过多项式插值简单地计算 $R(x)$，因为它是一个阶至多为 $n-1 $ 的多项式，而我们知道其中的 $n$ 个取值（集合 $S $ 上的取值为零）。使用上述所有零值进行插值得到零多项式，因此，$R(x)=0$，$H(x)=Q(x)$。（译者注，一个有 $n $个解的 $<=n-1$ 次多项式必为零多项式）

回到我们的例子上，如果我们有一个编码了斐波那契数的多项式 $F$（因此，在 $x=\left {0,1…98\right }$ 上满足 $F(x+2)=F(x)+F(x+1)$，那么我可以通过证明多项式 $P(x)= F(x+2)−F(x+1)−F(x)$ 在该范围的取值为零来向你证明 $F$ 确实满足该条件： $H(x)=\frac{(F(x+2)−F(x+1)−F(x))}{Z(x)}$ ，其中 $Z(x)=(x−0)∗(x−1)∗...∗(x−98)$.

你可以自行计算 $Z(x)$（理想情况下会被提前计算出来），检查该等式，如果检查通过，那么 $F(x)$ 的确满足条件！

现在，退一步，留意一下我们做了什么。我们将一个步长 100 的计算（计算第 100 个斐波那契数）转换为单个多项式等式。当然，证明第 $N$ 个斐波那契数的取值意义不大，尤其是因为斐波那契数具有闭合形式。但你可以使用完全相同的底层技术，只需一些额外的多项式和更复杂的等式，就可以对任意步长的任意计算进行编码。

现在，如果存在一种使用多项式校验等式的方法，而且这种方法比检查每个系数快得多…

多项式承诺

再一次，事实证明，这样的方法是存在的：多项式承诺。最好把多项式承诺看作一种对多项式进行“哈希”的特殊方法，该哈希拥有额外特性，即你可以通过校验多项式哈希间的等式来校验多项式间的等式。 不同多项式承诺方案在适用等式类型上有着不同的特点。

下面是一些常见的例子，您可以使用各种多项式承诺方案（我们使用com(P)来表示“对多项式 $P$ 的承诺”）：

• 相加：给定$ com(P)$、$com(Q)$ 和 $com(R)$，检查是否满足 $P+Q=R$
• 相乘：给定 $com(P)$、$com(Q)$ 和 $com(R)$，检查是否满足 $P∗Q=R$
• 在某个点上求值：给定 $com(P)$、$w$、$z$ 和一个补充证明（或“见证”）$Q$，验证 $P(w)=z$

值得注意的是，这些原语可以相互组合。如果支持加法和乘法，那么你可以这样计算：为了证明 $P(w)=z$，你可以构造出 $Q(x)=\frac{{P(x)−z}}{{x-w}}$ ， 然后验证者可以验证:

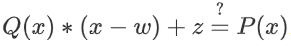
这行得通是因为如果存在这样一个多项式 $Q(x)$，那么 $P(x)−z=Q(x)∗(x−w)$，这意味着$P(x)−z$ 在 $w$ 处等于零（因为 $x−w$在 $w$ 处等于零），因此$ P(x)$在 $w $ 处等于 $z$。

如果你能计算出某点的取值，那么你可以进行各种校验。这是因为有一个数字定理表明：大体上，如果一些包含了一些多项式的等式在一个随机选择的下标下成立，那么对多项式整体而言等式基本为真。因此，如果我们只有一个证明某点取值的机制，那么我们就可以通过一个交互式游戏进行验证，如我们的方程 $P(x+2)−P(x+1)−P(x)=Z(x)∗H(x)$：

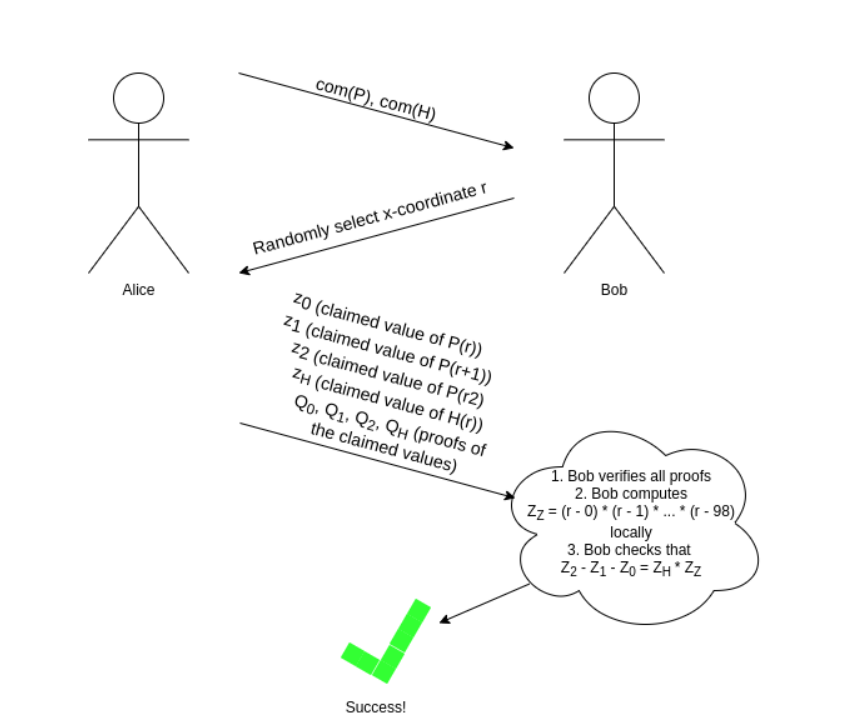
正如前面提到的，我们可以使用 Fiat-Shamir 启发式使其转化为非交互式：证明者可以令 r=hash(com(P), com(H))（其中 hash 是任一加密哈希函数；它不需要拥有任何特殊属性）并计算 r。证明者不能通过挑选只“符合”特定 r 的 P 和 H 来进行“欺诈行为”，因为他们在选取 P 和 H 时不知道r！

快速回顾

• ZK-SNARK很难，因为验证者需要以某种方式检查计算中的数百万个步骤，而无需直接地检查每个单独的步骤（因为这会十分耗时）。

• 我们通过将计算编码为多项式来解决这个问题。

• 单个多项式可以包含无限大的信息量，而且单个多项式表达式（例如，$P(x+2)−P(x+1)−P(x)=Z(x)∗H(x)$ 可以代表无限个数间的方程。

• 如果你可以验证多项式等式，那么你同时在隐式地验证所有的数值等式（用任何实际 $x$ 下标替换多项式中的 $x$）。

• 我们使用一种特殊类型的多项式“哈希”，称为多项式承诺，以允许我们在极短时间内验证多项式等式，即使背后的多项式规模非常大。

那么，这些神奇的多项式哈希是如何工作的？

目前有三种被广泛使用的主流方案：bulletproofs, Kate and FRI。

• 这里是Dankrad Feist对Kate承诺的描述：https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html
• 这里是curve25519-dalek团队对bulletproofs的描述：https://doc-internal.dalek.rs/bulletproofs/notes/inner_product_proof/index.html，而这里是我的图解：https://twitter.com/VitalikButerin/status/1371844878968176647
• 这里是对FRI的描述，我写的...：https://vitalik.ca/general/2017/11/22/starks_part_2.html

哇，哇，别紧张。试着简单地讲解其中一个，不要把我带到更可怕的链接上

老实说，它们没有那么简单。这就是为什么所有的这些数学理论直到 2015 年左右才真正崛起的缘故。

请？

在我看来，FRI 是最容易理解透的（如果你愿意把椭圆曲线配对 elliptic curve pairings 看作黑盒，Kate 会更容易理解，但配对确实很复杂，所以总体来说我觉得 FRI 更简单）。

以下是 FRI 工作原理的简化版（简单起见，免去真正协议中的许多技巧和优化）。假设你有一个阶小于n的多项式$ P$。对$ P $的承诺是某组预选下标取值的默克尔根（例如，$\left { 0,1...8n-1 \right }$，尽管这并不是最高效的选取方式）。现在我们需要额外添加一些东西来证明这组取值来自一个阶小于 $n$ 的多项式。（译者注，需要验证多项式阶小于 $n$ 的原因是保证作恶者通过随机抽样概率尽可能低，给定多项式 $P$，一个基本拟合 $P$ 的另一个多项式 $Q$，也是能通过随机抽样的，但 $Q$ 的特点是其阶要足够大才能成功）

设 $Q$ 为仅包含 $P$ 的偶次项系数的多项式，而 $R$ 为仅包含 $P$ 的奇次项系数的多项式。因此，如果 $P(x)=x^4 +4x^3 +6x^2+4x+1$，则 $Q(x)=x^2+6x+1$，$R(x)=4x+4$（注意，这些系数的阶数“向下折叠”到范围$ \left [ 0...\frac{n}{2} \right ]$。

注意，$P(x)=Q(x^2) +x∗R(x^2)$（如果这对你而言并不明了，那么停下来思考一下，并看看上面的例子，直到看懂为止）。

我们要求证明者提供$ Q(x)$ 和 $R(x)$ 的 Merkle 根。然后，我们生成一个随机数 rr，并要求证明者提供一个“随机线性组合”$S(x)=Q(x)+r∗R(x)$。

我们伪随机抽样了一大组下标（像之前一样，使用提供的Merkle根作为随机种子），并要求证明者在这些下标处提供 $P$、$Q$、$R$ 和 $S$ 的 Merkle 分支。在每个提供的下标处，我们校验：

• $P(x)$ 确实等于 $Q(x^2) + x∗R(x^2)$
• $S(x)$ 确实等于 $Q(x)+r∗R(x)$

如果我们做了足够校验，那么我们可以确信 $S(x)$ 的“预期”值与“提供”值最多（例如，1%）是不同的。

注意，$Q$ 和$R$ 的阶数都小于$ \frac{n}{2} $ 。因为 $S$ 是 $Q$ 和 $R$ 的线性组合，所以 $S$ 的阶数也小于 $\frac{n}{2}$ 。并且这反过来也成立：如果我们可以证明 $S$ 的阶数小于 $\frac{n}{2} $，$S$ 是一个随机选择的组合这一事实防止了证明者选取具有能够相互抵消的隐藏高阶因子的恶意 $Q$ 和 $R$ ，因此 $Q$ 和 $R$ 的阶都必然小于$ \frac{n}{2} $，并且因为 $P(x)=Q(x^2) +x∗R(x^2)$，我们知道 $P$ 的阶数必然小于 $n$。

从这里开始，我们简单地用 SS 重复上面的游戏，逐步“降低”我们关心的多项式的阶，直到多项式的阶低到我们可以直接校验的程度。

和前面的示例一样，这里的“Bob”是一个抽象概念，对密码学家在思维上论证协议非常有用。事实上，Alice 自己生成了完整证明，为了防止她作弊，我们使用 Fiat-Shamir：我们根据此前证明中生成的数据的哈希随机选取每个样本的下标或 $r$ 值。

（在该简化协议中）一个对 $P$ 完整的“FRI承诺”包括：

1. $P$ 取值的 Merkle 根

2. $Q$，$R$，$S_{1}$ 取值的 Merkle 根

3. $P$、$Q$、$R$、$S{1}$ 随机选取的分支，用于校验 $S{1}$ 是否正确地从 $P$ “归约”而来

4. 正如步骤（2）和（3）中所述，Merkle 根和随机选择的分支，一直进行降阶归约操作，$S{2}$ 由 $S{1}$ 归约而来，$S{3}$ 由 $S{2}$ 归约而来，直到归约到某个阶 $S{k}$（共重复 $≈log{2}(n)$次）

5. $S_{k}$ 的完整 Merkle 树取值（因此，我们可以直接校验）

流程中的每步都可能会引入一些“误差”，但如果您进行了足够多的检查，那么总误差将低到你可以证明 $P(x) $在至少 80% 的下标处等于一个阶小于$ n $的多项式。这足以满足我们用例的需求：如果你想在 zk-SNARK 中作弊，你需要对少数值进行多项式承诺，其多项式的取值会在多处不同于真正阶小于 $n$ 的多项式，因此任何对其进行 FRI 承诺的尝试都会失败。

此外，您仔细检查一下，FRI 承诺中对象的总数和大小是 O(log阶)，因此，对于大型多项式，承诺实际上比多项式本身小得多。

为了检查这类不同多项式承诺间的等式（例如，给定对 $A$、$B$ 和 $C$ 的 FRI 承诺，检查 $A(x)+B(x)=C(x)$），只需简单地随机选择很多下标，要求验证者提供在每个多项式的这些下标处的 Merkle 分支，并验证等式在每个下标处成立即可。

上面描述的是一种效率极低的协议；有很多代数技巧可以将协议效率提高约 100 倍，如果你想要一个切实可行的协议，比如在区块链交易中使用，你需要使用这些技巧。特别是，例如，$Q$ 和 $R$ 实际上不是必要的，因为如果你非常聪明地选择取值点，你可以直接从$ P$ 的取值重构出所需 $Q$ 和 $R$ 的取值。但是上面的描述应该足以让你确信多项式承诺从原理上是可行的。

有限域

在上述描述中，有一个隐含的假设：多项式的每个单独“取值”都很小。然而，当我们处理的多项式很大时，这显然不是真的。如果我们取上面的例子，$628x^{271}+318x^{270}+530x^{269}+...+69x+381$，他编码了 tau 的 816 位，并且在 $x=1000$ 时计算取值，得到...一个 816 位数字，包含了 tau 的所有这些数字。（译者注，因为代入 1000 时各个系数并补充和）因此，我们还需要增加一样东西。在具体实现中，我们在此所做的所有运算都不会使用实数域上的“常规”运算，而会使用模运算来完成。

我们将所有算术运算如下重新定义。我们选取一些素数“模数” p，% 运算符意味着“取其余数”：15 % 7=1，53 % 10=3，等等（注意，结果总是非负的，例如 −1 % 10=9 )。我们重新定义：

• x+y⇒(x+y) %p
• ∗y⇒(x∗y) %p
• $x^{y}⇒(x^{y})$ %p
• x−y⇒(x−y) % p
• $x/y⇒(x∗y^{p−2})$ % p

以上规则都是自洽的。例如，若 $p=7$，则：

• 5+3=1 (as 8%7=1)
• 1−3=5 (as −2%7=5)
• 2⋅5=3
• 3/5=2 (as ($3⋅5^5$)%7=9375%7=2)

更复杂的恒等式（如分配律）也成立：$(2+4)⋅3$ 和 $2⋅3+4⋅3$ 的结果均为 $4$。偶数定则（如 $a^2 − b^2=(a−b)⋅(a+b)$）在这种新运算中依然成立。

除法是最难的部分；我们不能使用常规除法，因为我们希望值始终为整数，而常规除法通常会得到非整数的结果（如 $3/5$）。我们使用费马小定理来解决这个问题，其表明对于任何非零 $x<p$，$x^{p−1}$%p=1 成立。这意味着 $x^{p−2}$ 得到一个这样的数，若再乘 $x$ 一次，就会得到 $1$，因此我们可以认为 $x^{p−2}$（整数）等于$ \frac{1}{x} $ 。计算模除的一种更复杂但更快的算法是扩展欧几里得算法，python 实现见此。

因为数字的“回环”方式，模运算有时被称为“时钟数学”

通过模运算，我们创造了一个全新的算术系统，它和传统算术一样是自洽的。因此，我们可以讨论该域中的所有同类结构，包括我们在“常规数学”中讨论的多项式。密码学家喜欢使用模数学（或者，更一般的，“有限域”），因为任何模运算结果的大小都会有界-无论你做什么，值都不会“超出”集合 $\left { 0,1,2…p−1 \right }$。即使计算有限域中一个一百万次多项式，也不会得出一个集合以外的值。

将计算转化为一组多项式等式更具意义的例子？

假设我们想要证明，对于某些多项式 $P$，满足 $0≤P(n)<2^{64}$ ，而不揭露 $P(n)$ 的实际值。这是一个区块链交易中的常见用例：你希望证明交易后账户余额非负而不揭露余额值。

我们可以用以下多项式等式对此进行证明（简单起见，假设 $n=64$）：

• $P(0)=0$

• 在 $\left { 0…63 \right }$ 范围内，满足 $P(x+1)=P(x)∗2+R(x)$

• 在$ \left { 0…63 \right }$ 范围内，满足 $R(x)∈\left { 0,1 \right }$ 后两个命题可以重新表述为如下所示的“纯”多项式等式（在上下文中，$Z(x)=(x−0)∗(x−1)∗...∗(x−63)$):

• $P(x+1)−P(x)∗2−R(x)=Z(x)∗H1(x)$

• $R(x)∗(1−R(x))=Z(x)∗H{2}(x)$ (注意此处的技巧：$y*(1-y)=0$ 当且仅当 $y∈\left { 0,1 \right }$ 核心思想是$ P{i}$ 的依次取值逐位地构建了 $P_{n}$ 的值：如果 $P(4)=13$，那么达到P(n)的取值序列将为：$\left { 0,1,3,6,13 \right }$。在二进制中，1 是 1，3 是 11，6 是 110，13 是 1101；注意，只要 $R(x)$ 为 0 或 1，$P(x+1)=P(x)*2+R(x)$ 就会一直向末尾添加一位。任何 $0≤x<2^{64}$ 范围内的数字可以通过这种方式在 64 步中构造出来，而任何此范围外的数字都不能通过这种方式构造出来。

隐私

但这里有一个问题：我们怎么知道对 $P(x) $和 $R(x)$ 的承诺不会“泄漏”信息（使得能够揭示我们试图隐藏的 $P(64)$ 的确切值）？

这里有些好消息：这些证明是对大量的数据和计算生成的小证明。因此，一般来说，证明往往不够大，只能暴露一点点信息。但我们能从“只有一点点”推进到“零”吗？幸运的是，我们可以。

在这里，一个相当通用的技巧是往多项式添加一些“模糊因子”。当我们选定P时，将 $Z(x)$ 的小倍数加到多项式中（即，取随机 $E(X)$，令 $P′(x)=P(x)+Z(x)∗E(x)$）。这并不会影响命题的正确性（事实上，$P′ $在“在计算发生”的下标处的值与 $P$ 相同，因此它仍是有效的转义版本），但它可以在承诺中添加足够多的额外“噪声”，使得任何余下信息不可恢复。此外，对于 FRI，重要的是不要对计算发生范围的随机点进行采样（在本例中为 $\left { 0…64 \right } $）。（译者注，这样即使是同样的多项式也会让人猜不到）

我们能再回顾一下吗？？

• 最优秀的三类多项式承诺是 FRI、Kate 和 bulletProof。

• Kate在概念上是最简单的，但它依赖于非常复杂的椭圆曲线配对“黑盒”。

• FRI很酷，因为它只依赖哈希；它的工作原理是将多项式逐渐归约为阶越来越低的多项式，并在每步进行随机抽样检查，使用 Merkle 分支来证明等价性。

• 为了防止单个值大小的膨胀，我们不在整数上做算术运算和多项式运算，而是在有限域上做所有事情（通常是对一些素数 p 进行模运算）

• 多项式承诺天然支持隐私保护，因为生成的证明已经比多项式小得多了，因此多项式承诺只能暴露多项式中一点点信息。但我们可以往多项式添加一些随机性，将暴露的信息从“一点点”减少到“零”。

哪些问题仍在研究当中？

• 优化 FRI：已经有很多涉及精心挑选的取值域的优化，“DEEP-FRI”，以及一系列其他让 FRI更高效的技巧。Starkware 及其他人正在研究这块。

• 将计算编码为多项式的更佳方法：找出将涉及哈希函数、内存访问和其他特征的复杂计算编码为多项式等式的最高效方法仍是一个挑战。在这方面已经取得了很大的进展（例如，见 PLOOKUP)，但我们仍需更多的进展，特别是如果我们想将通用虚拟机执行编码为多项式的话。

• 增量可验证计算：如果随着计算继续能够高效地“扩展”证明，那就太好了。这在“单证明者”情况下很有价值，而且在“多证明者”的情况下也很有价值，特别对于不同参与者创建区块的区块链而言。最近一些在这方面的工作，请参见 Halo。

我想了解更多！

我的文章

• STARKs: part 1, part 2, part 3
• Specific protocols for encoding computation into polynomials: PLONK
• 本文没有提到的一些关键的数学优化：快速傅里叶变换

其他人的文章

• Starkware's online course
• Dankrad Feist on Kate commitments
• Bulletproofs

ECN的翻译工作旨在为中国以太坊社区传递优质资讯和学习资源，文章版权归原作者所有，转载须注明原文出处以及ethereum.cn，若需长期转载，请联系eth@ecn.co进行授权。

本文首发于：https://www.ethereum.cn/Technology/how-zk-SNARKs-are-possible