椭圆曲线深入解析（第三部分）

如果我们只能用目前所包含的内容来定义什么是椭圆曲线，我们可能会说：

它们是具有特定表达式的三次多项式，定义在有限域上，并结合了一种特殊的点加法方式。

虽然从技术上讲，这是准确的，但这并没有很好地展现椭圆曲线的价值。特别是因为它们存在的整个理由是被应用于加密算法中——到目前为止，我们并没有提到任何使椭圆曲线作为加密基础的吸引人的特性。

显然，我们漏掉了一些重要的信息。

公平地说，谈论 椭圆曲线 最终是有点误导的。因为实际上，实际上在加密中使用的椭圆曲线其实并不是 曲线，而是 群。

它们是什么？

没错，群。仅仅“椭圆曲线”这个名字并没有讲述完整的故事。称它们为椭圆曲线 群 更为合适，但更短的版本被广泛接受。

现在，群 是 对加密很有趣的。而我们对它们还没有太多介绍，所以我们从这里开始吧！

群（Groups ）

原则上，群是非常简单的结构。它们仅由两个简单的元素定义：一个 集合，和一个 二元 运算。有效的二元运算需要生成一个也属于该集合的结果。换句话说，它应该是如下形式的函数：

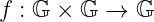
通常，我们不区分群 𝔾 和基础集合。通常将该集合称为“群”本身！

我们稍后将看到群为什么重要。但首先，让我们来看一个重要的例子。

我们在 早先的讨论 中花了很多时间讨论 有限域。这些域的基础集合仅是 模 p 的整数：

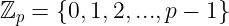
因为在 p 范围内，加法、减法、乘法和除法（模倒数）都是定义清晰的，所以这 behaves like a field。现在我们将 零 去掉：

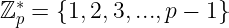
那么我就问：这仍然是一个域吗？

答案是 不。原因在于它在加法下并不 封闭：当我们将 1 和 p - 1 相加时，会得到 0，而 0 不属于我们的集合。

不过，在 乘法 的情况下，情况是可以成立的。

在这个群中，当两个数 a 和 b 相乘时，唯一能得到 0 的方式是结果是 p 的倍数——也就是说，p 是 a.b 的因子中的一部分。但如果 p 是 素数，那么这是不可能的——p 不可能仅仅出现在 a 和 b 的因数组合中。

因此，集合 ℤₚ* 的元素相乘绝不会得 0（模 p，且当 p 为素数时）。

我们看到，ℤₚ* 像一个群一样运作，因为它只支持一种操作（乘法）。称这个为 乘法群 也不奇怪。

有人可能会争辩说，它支持两种操作，因为我们可以计算乘法逆元。我们暂时就不深入讨论这一点。

群不一定是 有限 的——实际上，确实存在无限群。但由于与我们在 之前的帖子中提到的 相似的原因，我们希望使用有限群。通常，这被称为具有有限 阶 的群，而你可能猜测，这个 阶 是指群中的元素数量，或其 大小，或 基数。

Identity 与生成元（Generators）

群中的某些元素具有独特的性质，使它们显得特别。这就是群的 身份元素（identity） 的情况。

从概念上讲，身份元素非常简单。它是一个在群的二元运算中具有 完全无效 效果的元素。例如，在我们的 整数乘法群 中，我们可以很容易地看到 1 是身份元素，因为对于群中的任何数字 a：

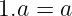
每个群必须有一个身份元素。不过，有些可能不那么显而易见。

然后，我们有 生成元。这个想法同样相当简单：取群中的一个元素 g，并与 它自己 执行群运算。

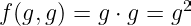
为了简单起见，暂时假设群是乘法群。因此，结果是 g² 而不是 2g。

拿结果，再次乘以 g，得到 g³。重复这个过程，直到结果再次为 g。

模 p 的整数乘法群是 循环的——不仅是有限的，经过足够多次运算后，你会回到同一个生成元。就像时钟上的数字一样！

如果在这个迭代过程中你看到群中的 每个元素，然后才重新获得 g，那么我们说它 生成 该群，或者说它是该群的一个 生成元。通常用以下符号表...