Uniswap V3 详解
根据sqrtPriceX96计算当前Tick
- RareSkills
- 发布于 2025-05-07 08:55
- 阅读 2877
本文解释了Uniswap V3协议中如何将sqrtPriceX96转换为tick,以及如何从tick转换回sqrtPriceX96,讨论了相关的数学公式和代码实现,以及如何在Python中进行计算,最后通过练习,帮助读者理解如何在实际的Uniswap V3池中进行这些转换。
在之前的章节中,我们看到协议存储的是价格的平方根而不是价格本身。因此,有必要将 tick 与固定点 Q64.96 格式的价格平方根联系起来。
在本章中,我们将探讨如何在 sqrtPriceX96 和 tick 之间进行转换。
协议存储了 tick 索引
一个 tick 是一个离散的价格,由公式 p(i)=1.0001i 给出,其中 i 称为 tick 索引或简称为 tick。有了 tick 索引,就可以唯一地确定 tick 价格,反之亦然。由于存储 tick 索引 i 比存储 p(i) 占用的位数更少,因此协议存储 tick 索引而不是 tick 价格。
在本书中,我们将交替使用术语 tick (价格)和 tick 索引。在代码库中,名为 tick 的变量始终指 tick 索引 i。
计算 tick 索引,给定 sqrtPriceX96
首先,我们回顾价格平方根与变量 sqrtPriceX96 之间的关系:
(sqrtPriceX96296)=p
因此,价格和 sqrtPriceX96 之间的关系是通过取两边的平方来给出的。
(sqrtPriceX96296)2=p
由于价格和 tick 索引之间的关系是 p=1.0001i,我们有
(sqrtPriceX96296)2=1.0001i
为了根据 sqrtPriceX96 确定 tick 索引 i,我们取上述等式两边的对数。
log((sqrtPriceX96296)2)=log(1.0001i)2log(sqrtPriceX96296)=ilog(1.0001)used thatlog(ab)=blog(a)i=2log(sqrtPriceX96296)log(1.0001)divided both sides by log(1.0001)
对数总是相对于一个底数而言。例如,如果 ba=c,则 logbc=a(log 以 b 为底)。但是,上面等式中的对数可以取任何底数。原因将在本章的最后一节中解释。
tick 索引是一个离散值
实际上,上述公式并不完全正确,原因之一是:sqrtPriceX96 是一个连续值,而 tick 索引 i 是离散的(一个整数)。因此,该值需要向下舍入。
这可以在下面的插图中看到,我们使用了一个可以在我们关于 tick 的文章中找到的工具。请注意,虽然价格不断变化,但该价格对应的 tick 始终是紧随其后的一个。
https://img.learnblockchain.cn/2025/05/07/lower-tick-anim.mp4
因此,tick 的准确公式是:
i=⌊2log(sqrtPriceX96296)log(1.0001)⌋
其中符号 ⌊…⌋ 表示向下舍入,例如,⌊3.14⌋=3。
计算 sqrtPriceX96 给定 tick 索引
要从 tick 索引计算价格的平方根,我们从公式开始
(sqrtPriceX96296)2=1.0001i
然后,取两边的平方根并乘以 296,
sqrtPriceX96296=1.0001isqrtPriceX96=1.0001i⋅296
从代码库中的 tick 到价格以及反之亦然
Solidity 中 tick 和 sqrtPriceX96 之间的转换由 TickMath 库 处理,由于在 Solidity 中实现 log 和平方根的复杂性,将在单独的章节中进行研究。
它包含两个函数:getSqrtRatioAtTick 和 getTickAtSqrtRatio,它们执行 sqrtPriceX96 和其对应的 tick 索引之间的转换,以及相反的转换。如下所示。
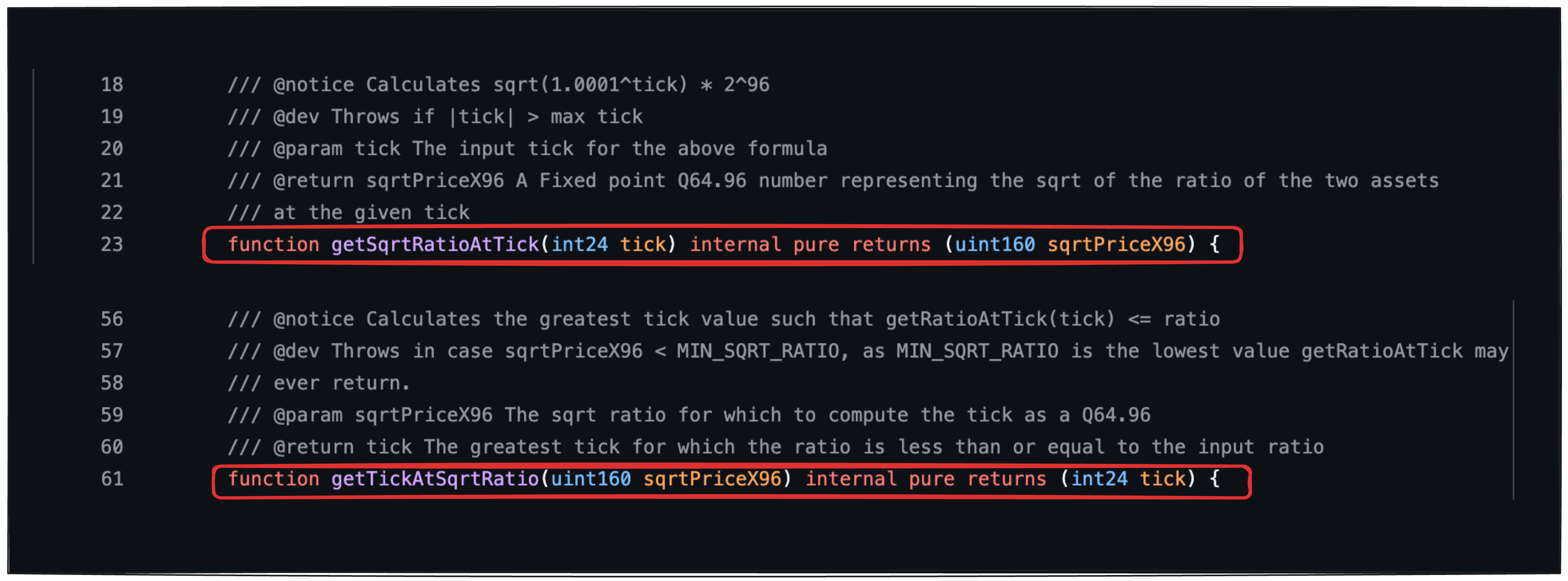
我们在上一节中看到了这些公式的数学原理。在本节中,我们将使用 Python 执行此计算。
getSqrtRatioAtTick 函数
Python 中的 getSqrtRatioAtTick 函数可以写成:
def getSqrtRatioAtTick(i):
return math.sqrt(1.0001 ** i)...- 学分: 69
- 分类: DeFi
- 标签: Uniswap V3 sqrtPriceX96 Tick TickMath库 价格计算 固定点数
