Solidity 优化 - 如何维护排序列表

• 原文链接：https://medium.com/bandprotocol/solidity-102-3-maintaining-sorted-list-1edd0a228d83 作者：Bun Uthaitirat
• Tiny 熊
• 译文出自：登链翻译计划
• 本文永久链接：learnblockchain.cn/article…

本系列文章有：

1. Solidity 优化 - 控制 gas 成本
2. Solidity 优化 - 编写 O(1) 复杂度的可迭代映射
3. Solidity 优化 - 维护排序列表

本文我们探索和讨论在以太坊独特的EVM成本模型下编写高效的Solidity代码的数据结构和实现技术。 读者应该已经对Solidity中的编码以及EVM的总体工作方式所有了解。

在上一篇文章中，我们讨论了(可以在每个元素上迭代的数据结构)如何在列表中添加元素或从列表中删除元素。这篇文章将扩展我们的数据结构，以维护链上已排序的链表。像上一篇文章一样，我们将通过展示每个函数的实现来进行解释。如果你准备好了，那就开始吧！

场景范例

像上一篇文章一样，我们依旧要创建一个“学校”智能合约，但是这次我们只保留了学生地址列表。我们需要根据他们的分数来维持他们的排序，老师可以在学生中增加或减去他们的分数，并且可以保证学生列表仍然可以随时按分数保持顺序。最后一个要求是我们可以列出排名前k的学生，以奖励表现良好的学生。

函数需求

让我们考虑一下满足所有要求所需的函数，需要实现5个函数。

1. 将新学生添加到具有分数排序的列表中
2. 提高学生分数
3. 降低学生分数
4. 从名单中删除学生
5. 获取前K名学生名单

实现

但是，在开始实现每个函数之前，我们需要设置基础数据结构(数组，映射等)，我们使用上一篇文章中的可迭代映射。创建映射以存储分数并为每个函数编写接口，框架代码如下所示：

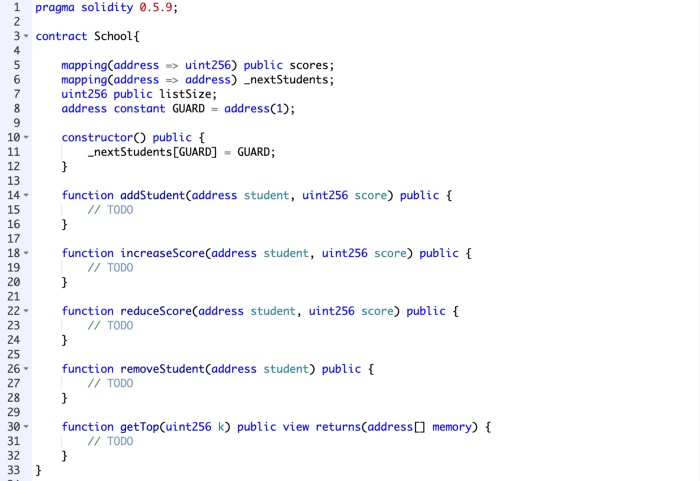
注意：GUARD是列表的头。

添加带有分数的新学生 addStudent

让我们从第一个函数 addStudent 开始。与普通的可迭代映射有所不同的是，我们需要在正确的索引处插入新项目，而不是在列表的前面添加以维持我们的排序。

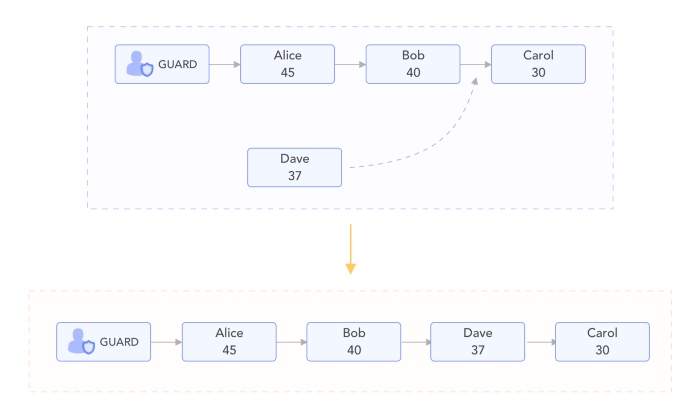<center>显示如何将Dave插入维护的排序列表中</center>

为了使代码易于阅读，我们创建了2个辅助函数来查找和验证新值的索引。

_verifyIndex 函数用于验证该值在左右地址之间。如果 左边的值 ≥ 新值 > 右边的值将返回true(如果我们保持降序，并且如果值等于，则新值应该在旧值的后面)

<center>验证索引函数</center>

_findIndex 帮助函数，用于查找新值应该插入在哪一个地址后面。从GUARD遍历列表，通过使用_verifyIndex检查来找到有效的索引。此代码确保我们可以肯定地找到有效的索引

<center>查找索引函数</center>

addStudent 在有效索引地址后插入新项目，更新分数并增加listSize。

<center>添加学生函数</center>

从列表中删除学生：removeStudent

removeStudent 的实现与上一篇文章相同，因为如果a≥b≥c，然后a≥c，在列表删除b之后仍是排序。

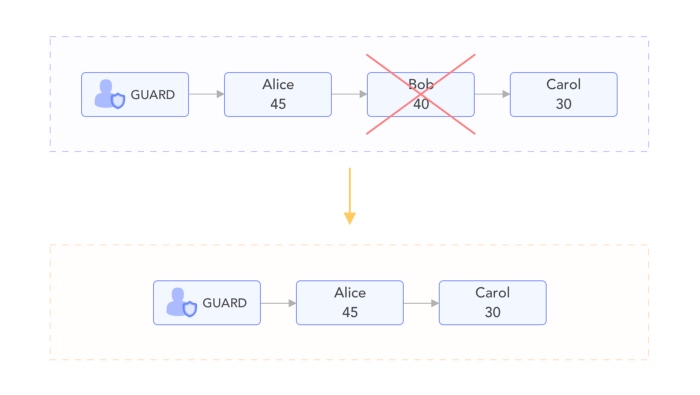<center>显示如何从列表中删除Bob</center>

辅助函数_isPrevStudent和_findPrevStudent

<center>检查前一个学生并找到前一个学生</center>

与上一篇文章相同的 removeStudent 不过需要清除 scores映射。

<center>删除学生函数</center>

更新学生分数：increaseScore 和 reduceScore

increaseScore和reduceScore可以使用相同的逻辑来实现，即将旧值更新为新值。主要思想是我们将旧项目临时删除，然后将其添加到新(或相同)索引中，该索引应具有新值，因此我们可以重复使用添加/删除函数。

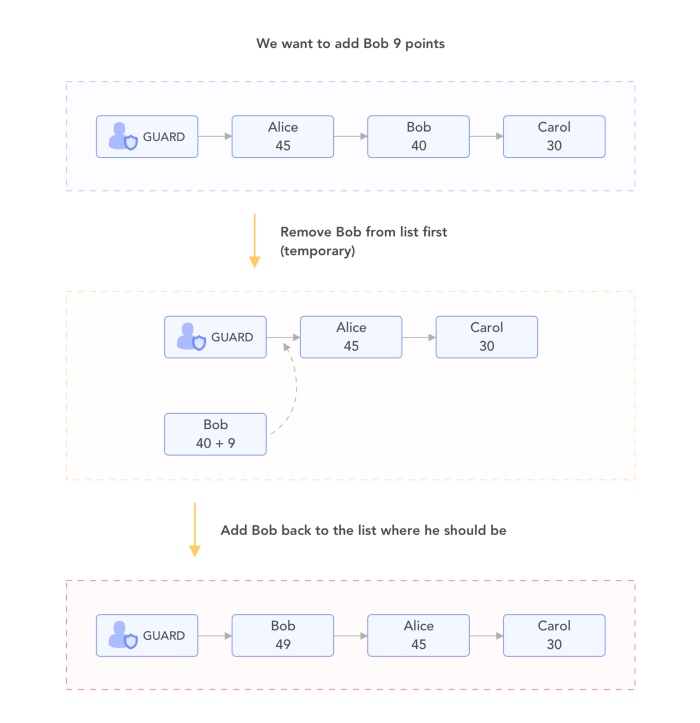<center>显示如何更新鲍勃的分数</center>

<center>更新分数函数</center>

注意：我们会检查条件，以确定新值是否适合相同的索引，这样我们不需要删除项目并将其添加到相同的值(这只是优化操作，可以节省1000 gas )

如果我们具有updateScore函数，则可以用一行代码来实现increaseScore和reduceScore函数。

<center>增加分数并减少分数函数</center>

获取前k名学生名单：getTop

这个函数没有什么花哨的，只是从GUARD循环开始，将地址存储到数组并返回该数组。容易吧？

<center>获取前k名学生函数</center>

代码已发布此处 , 代码如下：

pragma solidity 0.5.9;

contract School{

  mapping(address => uint256) public scores;
  mapping(address => address) _nextStudents;
  uint256 public listSize;
  address constant GUARD = address(1);

  constructor() public {
    _nextStudents[GUARD] = GUARD;
  }

  function addStudent(address student, uint256 score) public {
    require(_nextStudents[student] == address(0));
    address index = _findIndex(score);
    scores[student] = score;
    _nextStudents[student] = _nextStudents[index];
    _nextStudents[index] = student;
    listSize++;
  }

  function increaseScore(address student, u...