区块链中的数学--Merkle树承诺

写在前面

上一篇介绍了Kate承诺批量证明，本文继续介绍区块链中广泛使用的Merkle树承诺.

Merkle树结构

Merkle树是一种典型的二叉树结构，由一组叶节点，一组中间节点和一个根节点组成见下图，默克尔树最早由 Merkle Ralf 在 1980 年提出，曾广泛用于文件系统和 P2P 系统中。

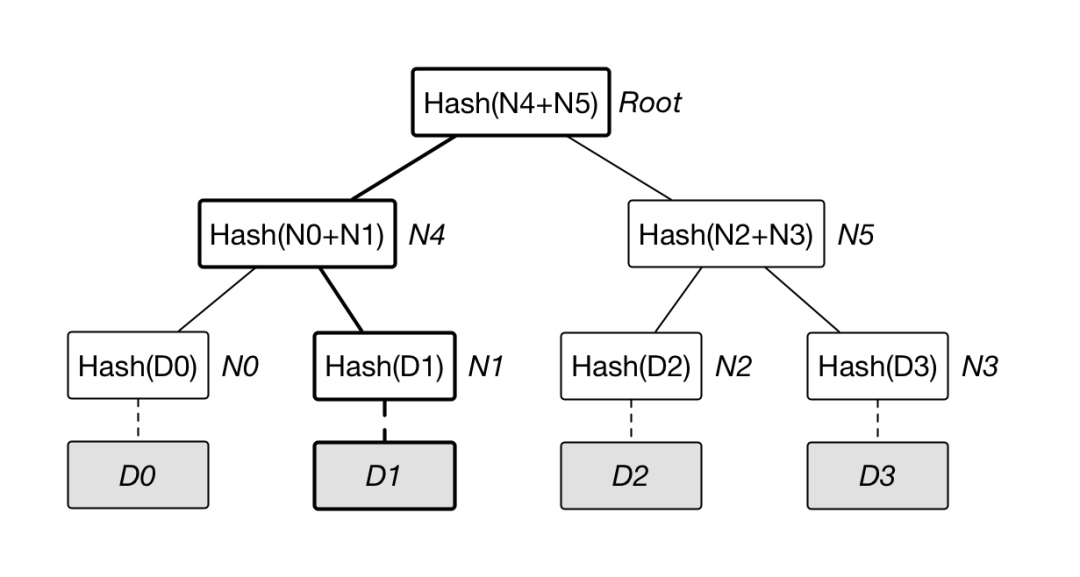
其主要特点为：

1. 最下面的叶子节点包含存储数据(或哈希值),非叶子节点（包括中间节点和根节点）都是它的两个孩子节点内容的哈希值。
2. 默克尔树逐层记录哈希值的特点，让它具有了一些独特的性质。例如，底层数据的任何变动，都会传递到其父节点，一层层沿着路径一直到树root。这意味root根的值实际上代表了对底层所有数据的“数字摘要”。

进一步地，默克尔树可以推广到多叉树的情形，此时非叶子节点的内容为它所有的孩子节点的内容的哈希值。

Merkle树应用

1. 证明某个元素存在特定集合中

通过构建集合的默克尔树，并提供该元素各级兄弟节点中的 Hash 值，可以不暴露集合完整内容而证明某元素存在。

例如上图中，证明D1存在,只需要提供 D1--> N0 -->N5-->Root 路径上元素集合，即可证明D1存在于根为root的merkle树叶子节点中。这个路径又称merkle树证明路径。

2. 数据压缩与比较

由于merkle树性质，树root实际上代表了对底层所有叶子节点数据的压缩值。 假如两组数据排序后构建默克尔树结构，当两个默克尔树根root相同时，则意味着所代表的两组数据必然相同。否则，必然不同。

如果选择Hash计算的过程十分快速，预处理可以在短时间内完成。利用默克尔树结构能带来巨大的比较性能优势。

3. 零知识证明

证明某个元素存在特定集合中，除了要证明的元素之外，并未泄露其他集合元素信息，因此具有零知识性质，可用在零知识相关应用中。

小结

merkle树在区块链中，用于压缩区块中打包的交易集合，其root值存在区块头中，作为交易列表不被篡改的证明。

以上内容，在很多merkle树的文章中基本都会提及，本文不同的是，将从密码学承诺的角度来看： 从密码学承诺的角度来看，merkle树是哈希承诺+树结构的组合，是哈希承诺的变种，同样基于哈希函数的不可逆，随机唯一性等性质来保证满足密码学承诺的性质：

绑定性（binding）：树root是叶子节点集合的承诺，一但公开便不能更改叶子集合。

隐藏性（hiding）：由于在承诺阶段只公布root，不会暴露原始叶子节点信息，在披露打开阶段，只公开路径上哈希值，也不会暴露其他叶子节点信息。

Merkle树如果说有其不足之处的话，当叶子节点的数量级非常大，树层级数变多，在打开验证节点需要的merkle树证明路径也就越长，数据量就越大，相对于此，前文描述的多项式承诺没有这个问题，所以Vitalik的一篇文章： https://ethresear.ch/t/using-polynomial-commitments-to-replace-state-roots/7095 畅想以后可能考虑使用多项式承诺代替现在已有的merkle树承诺。关于多项式承诺，参考前几篇历史文章。

好了，下一篇继续更多！

原文链接：https://mp.weixin.qq.com/s/KP8_locrhnJ9Mx5QGuTYAg 欢迎关注公众号：blocksight

相关阅读

区块链中的数学 - Kate承诺batch opening Kate承诺批量证明

区块链中的数学 - Kate承诺 Kate承诺完整流程

区块链中的数学 - 多项式承诺 多项式知识和承诺

区块链中的数学 - Pedersen密钥共享 Pedersen 密钥分享

区块链中的数学 - Pedersen承诺 密码学承诺--Pedersen承诺

区块链中的数学 - 哈希承诺 密码学承诺--hash承诺

区块链中的数学 - 不经意传输 不经意传输协议

区块链中的数学- BLS 基石（双线性函数）和配对 双线性映射（配对）

区块链中的数学 - BLS门限签名 BLS m of n门限签名

区块链中的数学 - BLS密钥聚合 BLS密钥聚合

区块链中的数学 - BLS数字签名 BLS签名及验证

区块链中的数学 - Feldman的可验证的密钥分享 Feldman可验证密钥分享方案

区块链中的数学 - Ed25519签名 Ed25519签名

Schorr签名与椭圆曲线 Schorr签名与椭圆曲线

区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析（中）