区块链中的数学 - Shamir密钥分享
- blocksight
- 发布于 2020-11-20 14:30
- 阅读 9926
密钥分享技术本质上是单一密钥的拆分管理,使用n份冗余储存,保证m份分片确定的秘密。这个秘密可以是私钥,也可以扩展成其他任意信息,如资产共同管理,谜语答案,秘密遗嘱等。
写在前面
上一节讲了比特币原始的多签和Schnorr聚合签名,比特币原始的多签是签名结果的累加,Schnorr聚合签名只保留最后聚合的签名结果,但是要求所有参与都要参与签名。
本文将介绍基于密钥分享的多签机制,既能实现m of n模式,也能实现减少签名结果的大小,实际上这属于阈值签名的范畴了。
密钥分享概念
密钥分享的基本思路是把一个密钥分成多份由多个参与方保存,如图密钥x,分成$x_1,x_2,...,x_n$共n份,分别由$s_1,s_2,...,s_n$保存,只要其中m份(m <= n)结合,就能恢复出原始密钥x,从而完成签名。 这种方式,从技术上来讲,本质上属于单签名,因为是一个私钥参与签名,不是多个私钥,可以看作广义的多签(由多个参与者共同参与)。
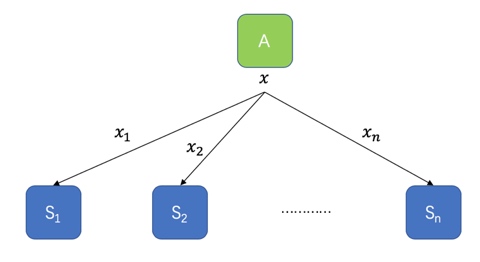
主要包括两个过程:密钥分割(split)和密钥恢复,下面从这两部分讲下如何实现。
密钥分享实现
我们先看下最早的Shamir(注:RSA中S代表的发明人)的实现方案。 Shamir使用一个多项式来隐藏密钥, $a_0$即是隐藏起来的密钥。
$a(x) =a_0+a_1x+a2x^2+...+a{m-1}x^{m-1}$
密钥分割(split):
随机生成$a1$到$a{m-1}$的系数值。在这条度为m-1次曲线上,任意取n个不同的点${(x_1,y_1),(x_2,y_2),...,(x_n,y_n)}$,将这些点分配给n个参与者,那么每个人得到的是一个密钥的一部分。
密钥恢复(recover):
m个人把各自的密钥碎片聚合在一起,即m个点代入多项式函数,可以确定一条唯一的曲线,即计算出${a_0,a_1,a2,...,a{m-1}}$的值,其中的就是要恢复的秘密。
由于m-1个点是随机生成的,通过这些点的曲线,在实数域理论上有无数条,概率上不会泄漏出关于$a_0$的任何有用信息。
这里隐含一个问题,如何根据已有的若干点,求出通过这些点的曲线? 这个求解过程叫做多项式插值。实现多项式插值有多种方法,本文介绍下其中最常见的拉格朗日插值法。
拉格朗日插值法
许多实际问题中都用函数来表示某种内在联系或规律,但是函数不是现成的,有很多只能通过实验和观测来推测。如对实践中的某个物理量进行观测,在若干个不同的地方得到相应的观测值, 拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。这样的多项式称为拉格朗日(插值)多项式。 数学上来说,拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。而这正是我们需要的。
使用方法:
在平面上有$(x_0,y_0),...,(x_n,y_n)$共n个点,设集合$ D_n= { 0,1,..., n-1}$ 是关于点的角标的集合,用n个多项式$P_j(x),j \in D_n$,对于任意 $k \in D_n$ ,都有$P_k(x)$, 集合 $B_k={i|i \not= k,i \in D_n}$,
满足
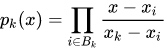
$P_k(x)$是n-1次多项式,且满足$\forall m \in B_k$ 并且$P_k(m)=0, P_k(x_k)= 1$ 。最后得:
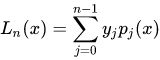
例如n = 4 得到:
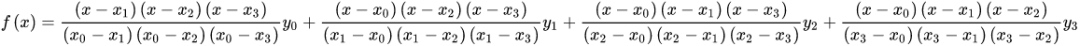
n = 3 ,去掉式子中最后一个即可。
至于该方法的推导验证过程,感兴趣的可以自行查阅,不再列出。
小结
密钥分享技术本质上是单一密钥的拆分管理,使用n份冗余储存,保证m份分片确定的秘密。这个秘密可以是私钥,也可以扩展成其他任意信息,如资产共同管理,谜语答案,秘密遗嘱等。
不仅实现了多方管理,也提供了一定的容错机制,允许最多n - m 份分片数据丢失。
拉格朗日插值法用来求解经过多个特定点的二维曲线函数,后面文章会再次用到。
本文的这种实现还存在一些弱点,到底有哪些不足和相应解决办法呢? 下一篇将继续介绍!
欢迎关注公众号:blocksight
相关阅读:
区块链中的数学 - 比特币使用的多签方式 比特币多签和Schnorr聚合签名
区块链中的数学 - 随机数和伪签名 随机数与伪签名构造
区块链中的数学 - EdDSA签名机制 EdDSA的发展及优点
区块链中的数学 - Ed25519签名 Ed25519签名
区块链中的数学-ElGamal算法 ElGamal算法签名及验证&实例演练
区块链中的数学-VRF基于ECC公钥体制的证明验证过程 基于椭圆曲线的VRF证明验证过程
Schorr签名与椭圆曲线 Schorr签名与椭圆曲线
区块链中的数学-Schnorr 离散对数签名及素数阶群构造(Schnorr 群) Schnorr签名及Schnorr群
区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析(中)
- 如何设计一个安全的稳定币系统 4937 浏览
- ZKsync 治理工具:安全提案验证 2972 浏览
- MPC vs 多签:交易所如何选择合适的钱包安全方案 1265 浏览
- 如何使用硬件钱包进行(不)盲签Safe多重签名交易 2259 浏览
- 玩转Sui多签钱包1:普通公钥多签钱包 @SUI Move开发必知必会 4896 浏览
- Uniswap v3 数学洞察系列翻译 —— 第六部分 共 6 部分 3810 浏览
- Uniswap v3 数学洞察系列翻译 —— 第五部分 共 6 部分 3928 浏览
- Uniswap v3 数学洞察系列翻译 —— 第四部分 共 6 部分 4360 浏览
- Uniswap v3 数学洞察系列翻译 —— 第三部分 共 6 部分 5222 浏览
- Uniswap v3 数学洞察系列翻译 —— 第二部分 共 6 部分 3327 浏览
- Uniswap v3 数学洞察系列翻译 —— 第一部分 共 6 部分 3902 浏览
- 田野调查:实现 MuSig2 4845 浏览

