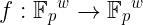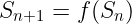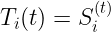密码学 101：STARKs
- Frank Mangone
- 更新于 1天前
- 阅读 84
密码学 101：STARKs
这是关于密码学的一系列文章的一部分。如果这是你看到的第一篇文章，我强烈建议从系列的开头开始阅读。
我们花了整整四篇文章讨论 SNARKs——所以到现在为止，我们应该非常熟悉这些框架背后的重要思想。主要是，证明的简洁性（通俗地说，简短性）非常吸引人。此外，它们还非常通用，因为它们依赖于算术电路来构建陈述。
但是，它们有一些我们可能需要担心的小问题。试图避免这些问题是深入探讨今天文章主题：STARKs 的动机之一。
免责声明
我会避免在这里深入探讨 STARKs 背后的一些想法。即便如此，这仍然会相当复杂……但我觉得这是一个很好的起点。像往常一样，把这篇文章看作是你继续自行探索的坚实基础！
什么是 STARK？
这次，缩写代表Scalable Transparent ARguments of Knowledge。
可扩展？透明？这些是什么意思？让我们做一个快速的比较练习，以更好地理解这些概念。
SNARKs vs STARKs
我想这里有两个主要的考虑点。首先，SNARKs需要一个可信设置。
作为提醒，可信设置是指某个参与者需要生成一些公共参数，并在此过程中丢弃一个秘密值。如果该秘密值没有被丢弃，那么他们可以随时伪造虚假证明，这无疑是一个很大的风险！
可信设置可能会非常谨慎地进行，但仍然总是存在秘密值未被丢弃的可能性，这确实削弱了我们创建的任何协议。因此，它们有时甚至被称为有毒废物。
相比之下，透明协议不需要可信设置。因此，它们消除了可信设置带来的潜在威胁。听起来很有趣，对吧？
另一方面，还有可扩展性的问题，这是我们在谈论 SNARKs 时甚至没有提到的一个术语。我们没有讨论的是：验证者如何知道验证什么？
答案是他们被允许读取所使用的算术电路。你可以想象，随着电路变大，这需要越来越多的时间——实际上，它需要线性时间。而电路可以变得非常大。所以这可能是一个很大的不行。
STARKs试图通过采取不同的方法来缓解这个问题。计算不是被建模为算术电路，而是作为状态转换函数，这在合适的情况下允许更快的验证时间。让我们仔细看看。
状态转换函数
总的来说，算术电路只是表示计算的一种方式。还有其他策略可以实现相同的目的。
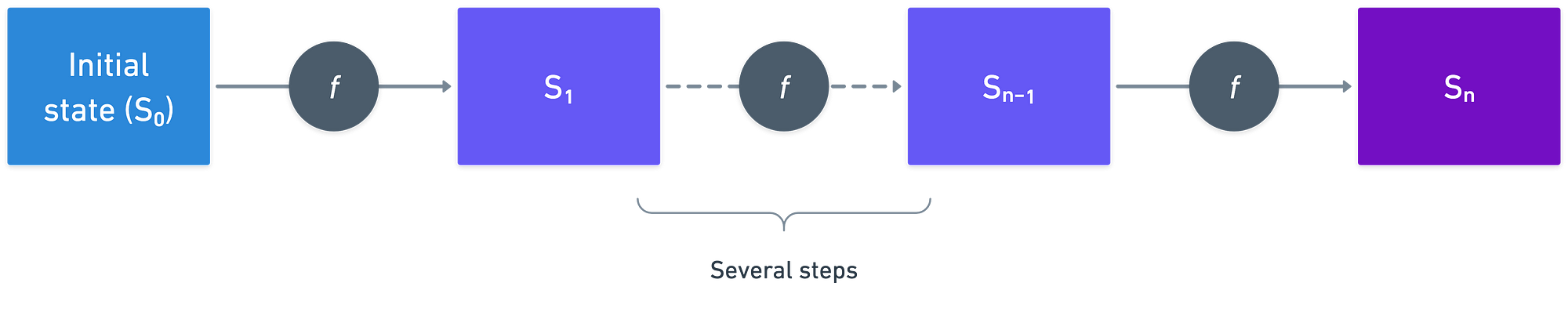
让我们想象一下，我们有一些计算可以表示为一系列步骤。你从某个初始状态开始，一次又一次地应用单一函数，直到达到最终状态。像这样：
整个计算由这个单一函数驱动——这就是，状态转换函数。没有什么能阻止我们编写一个算术电路来表示相同的计算——但请注意，这样的电路会比仅表示一个步骤的状态转换函数大得多。因此，读取前者需要更多的时间，而读取后者则不需要。
这就是为什么 STARKs 的缩写中有可扩展的原因：验证者可以在亚线性时间内运行。
那么，这个状态转换函数正式来说是什么呢？它只是一个这样的函数：
其中状态由一个长度为 $w$ 的向量表示，当然是由某个有限域的元素组成的。每个状态都是从前一个状态计算出来的：
我们关注的只是检查计算是否正确。或者，回到我们对 Plonk 的分析 ，检查计算轨迹是否满足一组约束。在这种情况下，约束总是由相同的状态转换函数给出的！
我们的计算轨迹将看起来像一个有$w$ 列和 T行的表格，代表我们经历的所有状态：
+---------------------+------+------+
| | x0 | x1 |
+---------------------+------+------+
| 初始状态 (S_0) | 1 | 1 |
+---------------------+------+------+
| 第一步 (S_1) | 2 | 3 |
+---------------------+------+------+
| 第二步 (S_2) | 5 | 8 |
+---------------------+------+------+
| 第三步 (S_3) | 13 | 21 |
+---------------------+------+------+
| 第四步 (S_4) | 34 | 55 |
+---------------------+------+------+
| 第五步 (S_5) | 89 | 144 |
+---------------------+------+------+
你可能认出来了——这是斐波那契数列！我们可以继续应用相同的状态转换函数来不断生成序列中的数字。
编码计算
当然，下一步与编码这个轨迹有关，以便稍后验证者可以检查由状态转换函数给出的约束是否成立。这个过程称为算术化。
在 Plonk 中，我们也进行了算术化。具体的技术实际上被称为 PLONKish 算术化 。
为了编码这些状态的转换，我们将使用一种称为算术中间表示的技术，简称_AIR。这个高大上的算法作为一个两步过程**工作：
- 将轨迹的每一列编码为一个多项式。
- 构建约束多项式。
在本系列的这一点上，我们对第一步已经非常熟悉。我们所需要做的就是将每一行的值分配给一些索引输入值 t（代表步骤），如下所示：
这就是，步骤 t 时状态的第 i 个分量
与 SNARKs 一样，步骤 t 实际上不是一个整数，而是一个单位根！所以，它实际上属于集合：
自然地，我们将获得 w 个多项式，每列一个——它们被称为轨迹多项式（因此用T来表示它们）。当然，我们通过 插值 获得它们。
第二部分涉及对状态转换函数本身进行编码。仔细观察，我们会发现它由 w 个独立函数 组成，每个状态组件对应一个函数：
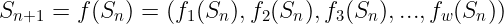
每个这些函数组件都需要使用 轨迹多项式 写成一个约束。让我们以斐波那契例子作为练习。很容易看出，该函数可以表示为：
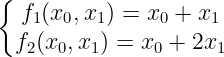
基于此，我们可以定义这些多项式，它们应该在单位根处评估为 0：
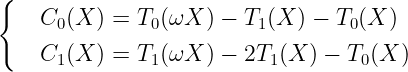
记住，乘以 omega 会将我们移动到下一步！
因此，如果验证者能够查询轨迹多项式在 $t$ 和 $ωt$ 处的值，他们应该能够检查表达式是否真的评估为0，这确保了计算满足状态转换函数 ！
如果验证者拥有这些约束多项式，他们可以简单地运行上述检查。但由于我们稍后会讨论的原因，他们从未真正得到这些多项式。我们现在知道的是，约束多项式可以从轨迹多项式中导出——所以让我们想象这样做是为了减少冗余。
好的，我们已经编码了我们的轨迹。还有一些额外的操作需要进行——但我们稍后会讨论。就像 Plonk 一样，编码对于我们创建一个框架是必要的，在这个框架中，验证者可以查询一些值并进行一些检查。
这是否让你想起了什么？是的，我们需要一个 交互式 Oracle 证明。
回到 IOPs
当我们探索 Plonk时，我们看到 交互式 Oracle 证明（ IOPs）是验证者查询多项式特定评估的一种方式——或在特定点请求开口(openings)。通过这些开口，他们可以验证围绕这些多项式的某种类型的声明。
例如，在 Plonk 中，我们看到如何构建 IOPs 来检查多项式在给定集合上为零。
我们将进行大致相同的过程。想法是验证者不需要检查每个转换约束，而只需检查一些随机样本，他们将请求开口。
不过，对于STARKs，我们不会使用与 Plonk 相同的 IOP。取而代之的是，我们将使用一种称为 快速里德-所罗门交互式 Oracle 接近证明(Fast Reed-Solomon Interactive Oracle Proof of Proximity)，简称FRI。
不过，好消息是——这个名字很花哨的技术使用了一个我们已经在系列中介绍过的主要成分：默克尔树！
交互式 Oracle 证明通常需要一个承诺方案。因此，我们将首先描述 FRI 的承诺方案是如何工作的。
给定一些多项式 P(X)，我们可以选择一些 评估域 D，这只是我们将用来生成P值的一组X值：
在 D中评估P(X)仅产生另一组值，即：
这个集合有时被称为里德-所罗门码字。我们将对其进行的操作是将其放入默克尔树中。通过计算树的根，我们获得的本质上是对所有这些 $P(X)$ 评估的承诺。很整洁！
使用默克尔树结构允许我们执行一个来回（sigma）协议，使验证者可以请求秘密多项式的值，并检查它们是否正确（或至少与承诺一致）。这是通过默克尔证明完成的，有时也称为认证路径。
为什么选择默克尔树？
当将其与其他承诺方案（如KZG 方案）进行比较时，我们可以看到有一些关键差异与我们的需求非常契合。
第一个关键差异与透明性有关。你看，基于默克尔树的承诺方案不需要设置。与其他方法相比，它减轻了未丢弃秘密参数的可能性，这对任何证明系统的安全性都是一种威胁。
其次，我们必须考虑可扩展性和效率。默克尔树在处理大量数据时非常高效——由于树结构，证明的大小是对数级的，正如我们之前提到的。像 KZG 这样的方案对输入数量是线性的，使得它们的可扩展性不太好。此外，承诺的数据只是有限域上的多项式评估——与 KZG 使用的椭圆曲线群操作相比，这些操作成本较低。
我们还可以研究我们方法的密码假设。可以说，基于默克尔树的结构的主要成分是哈希函数，而 KZG 的情况是配对。目前尚不清楚基于配对的方法的安全性将如何随着量子计算的出现而演变（在后续文章中会有更多讨论！），而哈希函数被认为在这种情况下更为稳健。
好的，抱歉信息量有点大！简而言之：
我们使用默克尔树作为我们的承诺方案，因为它适合我们的用例，出于透明性、可扩展性和效率的原因。
不过，FRI 还有更多内容。默克尔树只是拼图的一部分。现在，让我们回到我们的多项式。
回到编码
现在我们知道验证者如何在STARKs的背景下检查计算的正确性，以及多项式值是如何承诺的，我们可以仅凭这些部分设计一个第一迭代的证明系统。它将这样工作：
- 证明者承诺轨迹多项式
- 验证者读取状态转换函数，然后请求开口（通过 IOP）以检查约束是否成立
哦，要是这么简单就好了！
让我们看看证明者如何在这样的框架中作弊。有趣的时刻。
假设我们是一个恶意的证明者，意味着我们想让验证者相信一个无效的轨迹是正确的。假设我们的轨迹有_T_步。
无论出于何种原因，假设我们在某个步骤_t操纵轨迹——使得只有一个无效的状态转换，而��余的都是正确的。验证者查询那个_特定状态转换的可能性有多大？
很明显，答案是他们有一个_1 在 T的概率来查询到正好是无效的状态转换。即使他们进行多次查询，几率也不会增加多少，尤其当T_很大时。
这看起来不太安全！我们可以做些什么来改善这种情况？
增强安全性
我们的策略将类似于我们在 Plonk 中使用的零测试 。所以我建议先查看一下，如果你还没有的话！
跟踪多项式本身并不编码状态转换约束——约束多项式才是。我们需要以一种允许我们检查整个跟踪的全局一致性的方式来操作它们。听起来很棒，对吧？
因此，我们首先需要构建约束多项式。这些取决于我们的状态转换函数——回想我们的斐波那契示例，它们看起来像这样：
在这个简单的例子中，约束多项式的次数最多为 d。但它们完全可能具有高于 d 的次数，因为状态转换函数很可能包含乘法。
我们已经提到这些多项式在单位根处有根——也就是，评估域_D。这些值可以用来构建一个称为零化多项式或消失多项式_的多项式：
因为我们使用了每个$Cᵢ(X)$ 的根，当我们将$Cᵢ(X)$除以$Z(X)$时，我们得到另一个低次数的多项式，没有余数：
自然地，我们称这些为商多项式。
你可能会问，它们有什么有趣之处？答案非常优雅：如果我们即使只稍微篡改了跟踪，那么原始约束多项式将不可被$Z(X)$ 整除，这意味着会留下某些余数。因此，如果我们采样一些随机值$x$，并发现：
那么很可能 $Cᵢ(x)$ 确实可以被 $Z(X)$ 整除，这意味着它满足状态转换约束。
别告诉我这不妙！
然而，有一点需要考虑：如果我们从集合$D$中采样$x$，那么$Z(X)$和$Cᵢ(X)$将 总是产生 $0$，这意味着我们剩下：
在这种情况下，$Qᵢ(X)$可能是任何东西。因此，我们实际上并没有在这里检查多项式的相等性。
STARKs通过扩展评估域来克服这个问题。也就是说，验证者可以从更大的域 $D’$ 中采样。$D’$ 和 $D$ 的大小比有一个特殊的名称——称为膨胀因子。其值通常介于2和8之间。
在$D’$中新增的点上评估$Z(X)$和$Cᵢ(X)$时，两者都不会产生零。因此，在这个扩展域中，我们的原始检查确实允许我们验证多项式的相等性。
顺便说一句，我想我之前没有提到过，但这种类型的检查有一个名字：它是 Schwartz-Zippel 引理的应用。我们在 Plonk 文章中也使用过它而未提及！
这是一个很大的进步！可惜，这还不够。
请让它停下来。
有一些微妙的方法可以通过这些新的安全措施作弊——为此我们需要进行另一个检查。
我认为这篇文章相当长。现在是喝咖啡休息的好时机！
破解系统
让我们再试一次作弊。
假设我们在某个步骤$t$修改了跟踪的值。但我们不仅仅是插值跟踪，我们还添加了一些更多的值到插值中。
在计算约束多项式时，会发生两件事：
- 它们在被篡改的步骤上不会评估为零，
- 它们的次数会高于预期。
我们检测恶意活动的策略是评估：
在评估域$D$内，这个检查将在被修改的步骤上失败，但在其他步骤上通过。问题是D之外，在扩展域 $D’$ 中会发生什么。
在那里，消失多项式将评估为某个非零值。因此，只要我们能够构建高次数多项式$Qᵢ(X)$和$Cᵢ(X)$ 来匹配上述条件……我们基本上又回到了原点。
问题就像我们最初的简单设置一样，但更糟：在 $D’$ 的大小（ $D’$ 的大小）中有一个 1的概率正好采样到检查不成立的值。可以说，这甚至更糟，因为 $D’$ 比 $D$ 大。
简而言之：我们完蛋了！
就是这样！我们迄今为止精心构建的系统被愚弄了。
幸运的是，有一种巧妙的方法可以抵御这种类型的攻击。
看，恶意证明者唯一能做我们描述的过程的方法是通过构建高于预期次数的跟踪多项式。而如果我们知道跟踪的长度，我们就知道预期的次数。
所以这就是我们的解决方案：检查这些多项式中的一些是否具有低次数。这将把一切联系起来。
作为一个细节：在 KZG 中，我们不需要这种检查，因为多项式的次数被编码到公共参数中。本质上，次数不是攻击者可以操控的东西。
检查低次数
现在，这才是我们选择 $FRI$的 真正 原因。让我们看看它是如何工作的。
我们将使用商多项式。我们想要检查它们的次数最多为 $d$ ，其中 $d$ 可以通过知道状态转换函数和跟踪中的步骤数来计算。
我们将应用的策略称为分割和折叠。其背后的粗略想法是将一个声明（在这种情况下，即评估对应于低次数多项式）分成两个一半大小的声明，并与一些不可预测的验证者输入结合。理解这一点的最佳方式是看到它的实际应用。
我们的多项式的次数最多为 d，所以我们可以这样表示：
$pᵢ$ 只是多项式的系数。我们可以将其分割为奇数和偶数幂，如下所示：
在哪里：
可能需要一点时间来理解这一点。慢慢来。
如果你仔细观察上面的表达式，你会注意到 (d + 1) / 2 可能不是整数，这就是一个问题。协议使用了一个有趣的技巧来确保这种情况，但我们在这里不讨论。
这两个多项式的次数是原始多项式的一半。
接下来，验证者被要求提供一个随机整数 $α$。然后这两个多项式被压缩成一个新的多项式，其次数减半（因此称为折叠，如同对折），如下所示：
通过了解 $P(X)$，我们可以为这个新多项式 $P * (X)$ 构建 码字（也称为评估）。我不会详细介绍这是如何发生的，但你可以想象这只是进行一些替换而已。如果你感兴趣， 这篇文章有详细介绍。
这个过程的结果是一个简化多项式的码字（再次强调，评估），在一个大小减半的域中，证明者对此进行承诺。
此时，验证者拥有对 $P(X)$ 和 $P *(X)$ 的承诺，以及采样值 α 他们的目标是检查两个多项式是否一致——这意味着这里的关系应该成立：
我将留给你来检查这应该成立！这非常简单。
这是通过一个 共线性检查 完成的，这次我们不讨论。
真的，要全面理解 STARKs，有许多细微差别、优化和细节需要覆盖。我满足于在这篇简短的文章中捕捉协议的主要思想，但如果你感兴趣，还有更多内容可以探索。
一旦验证者检查多项式之间的关系是正确的，这个过程就简单地重复，使用 $P * (X)$ 作为新的起点。经过足够多的轮次后，证明者将得到一个常数，他们将其发送给验证者，明确表示他们已经完成了对原始码字的折叠！
这很多，我觉得我们只是触及了表面。尽管如此，这已经足够理解这一点：在这个简化过程中的轮次数允许我们建立一个我们开始时多项式的次数上限！
因此，这个过程允许我们证明一个多项式具有某种有界次数，正如我们之前所见，这对于确保原始轨迹没有被篡改以及一致性检查实际上有意义是很重要的。
总结
我们深入探讨了 STARKs 的内部工作原理。
将所有部分结合在一起，协议大致包括以下步骤：
- 证明者将计算轨迹算术化为轨迹多项式，并计算约束和商多项式，
- 然后证明者通过默克尔树对轨迹和商多项式进行承诺，
- 验证者请求一些开放以检查商多项式是否一致，
- 最后，使用 FRI 确保商多项式具有有界次数。
轨迹多项式对于边界约束检查是必要的，我没有涉及。只需知道它们是保证计算的初始和最终状态正确所必需的！
如果一切检查无误，验证者就接受证明。
将 STARKs 的复杂性简化为简单的解释是困难的。我们讨论的一些概念相当复杂，但其核心是，我们使用的是简单的元素和技术，以复杂的方式组织在一起以产生惊人的结果。
而且，正如任何复杂的密码系统一样，总有更多的东西可以探索。有关更多入门材料，请查看这篇补充文章 。此外，我强烈建议阅读这一系列文章以更深入地了解 STARKs ——但即便如此，你会发现有些细节被省略了！
是的，确实很复杂。
我真的希望这篇文章为 STARK 框架的一般概念提供了一些坚实的基础。密码学在不断发展，但学习这些技术背后的思想始终是更好地跟上未来发展的一个很好的练习！
话虽如此，我们系列的下一站将带我们更接近一个在当今密码学界备受争议的话题：后量子密码学，或 PQC。该领域的大多数方法基于我们尚未涉及的数学结构：环。这将是下一篇文章的主题。再见！
