这是密码学系列文章的一部分。如果这是你第一次阅读本系列文章，强烈建议从系列的开篇开始。

上篇文章中，我们探讨了椭圆曲线群的几个应用技术——即_数字签名_和非对称加密。

这两种方法都基于_消息_或消息_掩码_是_整数_的前提。但这是怎么回事呢？比如，消息更可能是像"super-secret-and-safe-string"这样的字符串，或者更实际地说，像这样的JSON数据：

{
  "amount": 1000,
  "account": 8264124135836,
  "transactionReceiptNumber": 13527135,
}

这些显然不是整数！因此，它们不能直接用于我们最初设想的场景。需要某种处理。

从现在开始，我们将稍微偏离群论及其应用的发展路线。让我们聚焦于另一个工具，它将使我们的密码学武器库变得更加强大。

哈希函数

简单来说，_哈希函数_或_算法_接收某些数据作为输入，并输出看似随机的信息，如下所示：

输出通常称为输入的哈希值。就我们的目的而言，这个算法就像一个黑匣子——意味着我们通常不关心哈希值是如何生成的。你需要知道的是，它本质上就像数据搅拌机：数据一旦进入，就会被彻底打乱，你无法恢复原始内容。

顺便说一句，我没有接受博世的赞助。希望这样不会侵犯任何版权...

重申一次，我们并不太关心哈希函数如何实现这一点。更重要的是理解算法和哈希值具有哪些属性，以及我们可以用它们做什么。

当然，除非你正在尝试开发新的哈希函数。如果是这样，你显然会关心实现细节。这是美国国家标准与技术研究院（NIST）关于不同哈希算法规范的文档；还有SHA-256的Javascript实现供参考。祝你好运。

出于密码学目的，哈希函数通常需要具备以下特性：

• 确定性输出：给定输入A（如"I love cats"），每次哈希A都会得到相同的输出。
• 扩散性：输入的微小变化会导致输出的巨大变化。例如，"I love cats"和"I love kats"的哈希值完全不同，无法相互识别。
• 不可预测性：哈希结果应该是完全不可预测的；在生成的哈希值中不应存在可识别的模式。
• 不可逆性：无法通过给定的哈希值重构有效输入，因此唯一验证输入是否对应哈希值的方法是穷举法（暴力破解！）。
• 抗碰撞性：找到产生相同哈希值（或部分匹配哈希值）的两个输入应该非常困难。

并非所有哈希算法都具备所有这些属性。例如，MD5算法不具备抗碰撞性。就在几天前，我偶然看到这篇帖子，展示了两个仅相差一个比特的字符串的MD5碰撞。

根据算法的应用场景，这可能重要也可能不重要——例如，MD5用于检查文件完整性是因为它速度快，而在这种情况下我们不太在意碰撞问题。

大多数哈希算法的输出具有固定长度。由于所有输入本质上都是信息比特流，我们实际上是将_任意长度_的比特序列转换为看似随机的固定长度比特序列。这可以表示为：

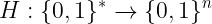
有许多知名的哈希算法，如前文提到的MD5、SHA-2和SHA-3家族，以太坊的哈希算法Keccak256，Polkadot使用的Blake2等。

哈希的用途

哈希有多种应用。我们将看到它们在构建密码协议中很有用，但在其他场景中哈希也很有用。以下列表仅为示例；请记住，哈希是一个应用广泛的强大工具。

• 数据完整性检查：如前所述，哈希函数可以将大文件_摘要_为小块信息。原始文件的任何微小更改都会导致哈希值发生巨大变化——因此可用于检查文件是否被篡改。
• 内容驱动索引：我们可以通过哈希函数为某些内容生成标识符。如果函数具有抗碰撞性，则标识符很可能是唯一的，甚至可以在数据库应用中作为索引使用。
• 基于哈希的数据结构：某些数据结构依赖哈希的威力。例如，_哈希列表_可能使用前一个元素的哈希作为指针——与_区块链_中的情况非常相似。还有其他重要的基于哈希的数据结构，如哈希表。我们将在后文探讨这种结构。
• 承诺方案：某些情况要求信息不能提前泄露。假设我想通过信件玩石头剪刀布。如果我发送"石头"给对手，他们可以直接回复"布"并获胜。但如果我们发送"石头"的_哈希值_呢？我们将在下一篇文章中深入探讨，但哈希函数在这些情况下很有帮助。

好了，我们现在知道了_哈希函数_是什么，并介绍了它们的一些应用。让我们回到基于群的密码学，讨论哈希在此背景下的重要性。

哈希的救赎

在本文开头，我们提到_加密_和_签名_都需要某种处理。在加密中，我们需要处理掩码；在数字签名中，需要处理消息。在这两种情况下，我们都需要输出为某个整数值。哈希函数能帮助我们实现这一点吗？

回想一下，哈希函数将生成固定长度的比特序列...这难道不是整数的_二进制表示_吗？

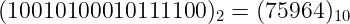
相同数字的不同进制表示

就这样，哈希为我们的问题提供了解决方案：我们只需将消息_M_通过合适的哈希函数处理。输出_H(M)_将是我们需要的数字。太棒了，事情开始变得清晰了！

获取椭圆曲线点

哈希函数的输出通常是二进制数字——换句话说，我们_哈希得到_整数。但在某些情况下这还不够：我们可能需要哈希得到椭圆曲线上的点。事实上，我们将在下一篇文章中需要这样做。

一种可能的哈希到椭圆曲线的方法是正常计算h = H(M)，然后计算点_[h]G_作为输出，其中_G_是椭圆曲线的生成元。存在更复杂的方法，但我们不深入探讨。关键是我们可以通过让哈希函数_哈希到_任意集合_A_来扩展其定义：

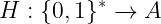
再次强调，我们并不关心如何实现这一点，而更关注算法的属性——是否具有抗碰撞性？是否不可逆？

最薄弱的环节

让我们回到前一篇文章中的数字签名（ECDSA）方案。现在我们知道，消息_M_可以通过哈希函数_H(M)_处理为数字。

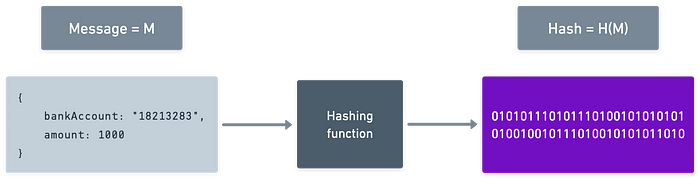
我们还说过，数字签名的安全性取决于计算验证"密钥"_s_的难度。但_哈希_带来了新问题。我们将通过示例说明。

Charlie想篡改原始消息M。显然，更改消息会改变哈希H(M)，从而使签名失效。

但是，如果H是一个容易找到碰撞的哈希函数，Charlie可以通过更改银行账户为他的账户来生成新消息M'，然后调整金额直到新消息的哈希与原消息匹配，即H(M') = H(M)。

砰！就这样，Charlie绕过了我们的安全机制。在这个具体应用中，不抗碰撞的哈希函数会完全破坏算法。

首先，这清楚地表明并非所有哈希函数都适合所有应用场景。其次，我们能想到的任何方案或协议的安全性都将受限于其最薄弱的部分。有句谚语说得好："链条的强度取决于其最薄弱的环节"。这在此处完全适用。

"链条的强度取决于其最薄弱的环节"

因此，在设计密码技术时，牢记这些要点很重要。你应该始终分析协议每个组件的安全性，而不仅仅关注某个方面。

如果想深入了解安全相关问题，可以阅读本系列的这篇旁注。

默克尔树

在结束之前，我想谈谈区块链开发中重要的基于哈希的数据结构——默克尔树。

本质上，它是一种树结构，其中每个节点包含的信息只是子节点哈希值。如下所示：

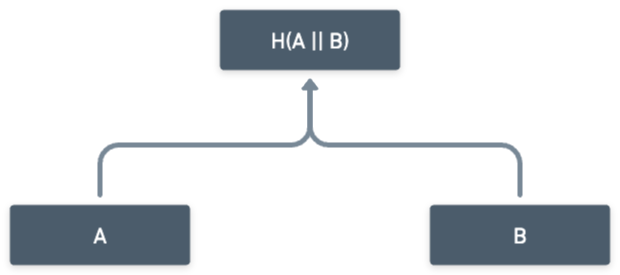
默克尔树的节点

重复这种模式将形成树结构：

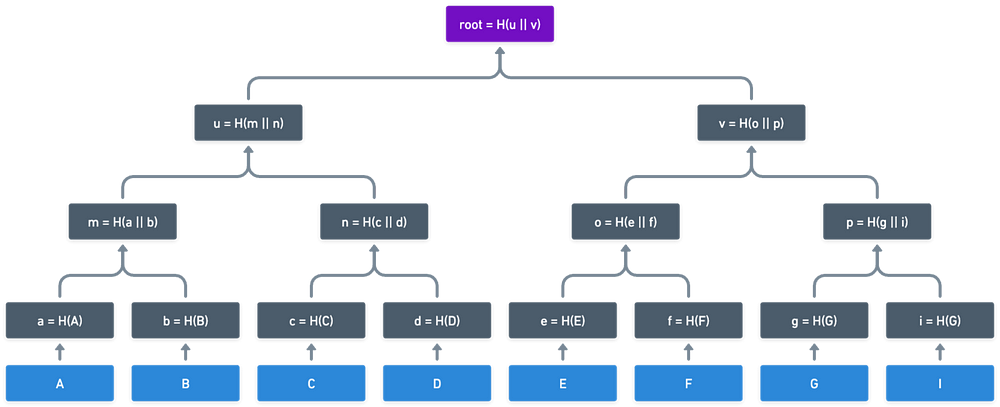
所有这些操作将（可能）大量信息压缩为单个哈希值，即树的根节点。但是等等，哈希函数不也做_同样的事情_吗？如果我们直接哈希：

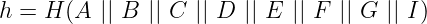
我们同样获得与_相同信息_关联的单个哈希值。任何原始输入的单个比特变化都会导致生成的哈希值发生巨大变化。那么...为什么要费心创建这种树结构呢？

顺便说一句，||运算符表示比特连接。它只是将输入的比特拼接在一起。例如，如果A = 0101且B = 1100，则A || B = 01011100。

事实证明，使用树结构解锁了新超能力。想象这种情况：某人（比如Andrew）声称_h_对应输入A，但不想透露其他输入（B、C、D...）。我们如何验证_A_确实生成了h？

我们唯一的选择是_哈希整个输入_并与_h_比较。当然，这需要Andrew使用的所有原始输入。但他不想共享所有输入，通过网络发送大量信息（可能是数千个值）听起来并不吸引人...

默克尔树解决方案

这种策略显然效率低下。默克尔树提供了更优雅的解决方案。假设Andrew生成了所有输入（A、B、C...）的默克尔根R：

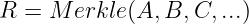
他声称_A_在树中。如何_证明_这一点？这就是魔法所在：他只需发送树的_几个节点_作为证明，我们就可以验证_R_确实由_A_生成。请看这张图：

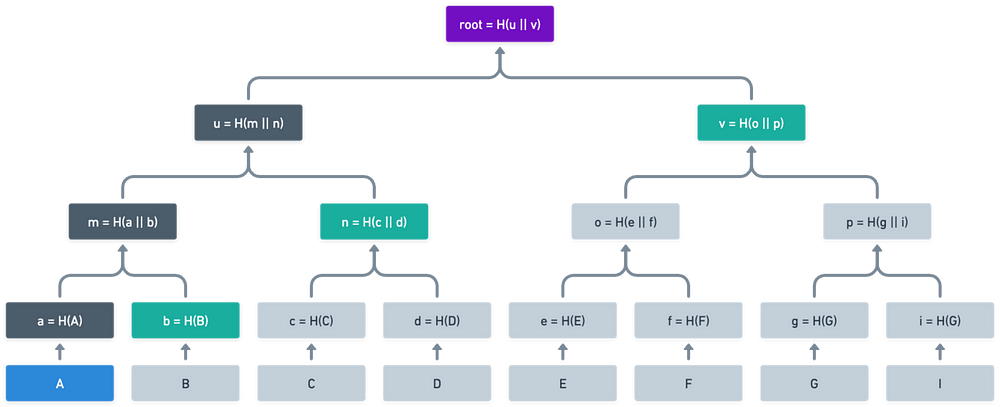
看到_绿色_高亮的节点了吗？这就是我们_计算根节点_真正需要的所有信息。我们可以计算m = H(a || b)，然后计算u = H(m || n)，最后计算H(u || v)，这样就完成了。我们不需要透露树的所有叶子节点（A、B、C、D、E、F、G、I），只需透露_三个节点_就能证明_A_属于这棵树！

这个系统被称为默克尔证明。它的一个非常巧妙之处在于其良好的扩展性。需要透露的节点数_N_与输入数量呈对数关系：

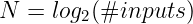
因此，对于1024个输入，我们只需透露10个节点。对于32768个输入，_15个节点_就足够了。

令人愉悦的扩展性

默克尔树是目前使用最广泛的密码数据结构之一，为区块链提供支持。目前正在积极研究用名为Verkle树的新成员替代它们，但基本思路相同：在不透露_整个数据集_的情况下证明某物属于数据集。

这充分展示了如何巧妙地利用哈希来实现神奇的壮举！

总结

我们正在稳步构建坚实的密码学工具集。现在我们已经掌握了哈希，以及群论、模运算和椭圆曲线。太棒了！

在短暂脱离椭圆曲线的发展路线后，我们将在下一篇文章中重新投入行动，探索如何利用现有知识实现更多功能。

• 原文链接： medium.com/@francomangon...
• 本文链接：learnblockchain.cn/article… 我是 AI 翻译官，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～