区块链技术解析(3):深入理解STARKs
- Vitalik Buterin
- 发布于 2018-07-23 15:19
- 阅读 1531
本文详细介绍了STARK的实现,特别是通过Python代码展示了如何利用MIMC函数生成STARK证明。文章深入讨论了STARK的计算复杂性、验证过程及其在零知识证明中的应用。
特别感谢 Eli ben Sasson 的友好协助,和 Chih-Cheng Liang 以及 Justin Drake 的审核,感谢 Ben Fisch 建议采用反向 MIMC 技术用于 VDF(论文在这里)
触发警告:数学和大量 Python
作为该系列文章的 第 1 部分 和 第 2 部分 的后续内容,本篇文章将涵盖实际实现 STARK 的样子,以及 Python 中的实现。STARKs("可扩展透明知识证明")是一种生成证明的方法,证明形式为 f(x)=y,其中 f 的计算可能需要很长时间,但证明可以很快得到验证。一个 STARK 是 “双重可扩展”的:对于一个执行 t 步的计算,生成一个证明大约需要 O(t⋅logt) 步,这可能是最佳的,而验证则需要 ~O(log2t) 步,对于即使是中等大的 t 值,这远远快于原始计算。STARKs 还可以具备隐私保护的 “零知识” 特性,尽管我们在这里应用它们的用例,即制作可验证延迟函数,并不需要这个特性,因此我们不需要担心它。
首先,一些免责声明:
- 这段代码尚未经过彻底审核;在生产用例中的正确性不予保证
- 这段代码非常不优化(它是用 Python 编写的,你期待什么)
- “现实生活” 中的 STARKs(即 Eli 和他的团队所实现的生产实现)倾向于使用二进制域而非素数域,原因是应用特定的效率;然而,他们在著作中强调这里描述的基于素数域的 STARK 方法是合理的并且可以使用
- 没有 “唯一真实的方法” 去做一个 STARK。它是一个广泛的密码学和数学构造类别,随着不断的研究,根据不同的应用,存在不同的最佳配置以降低证明者和验证者的复杂性并提高可信性。
- 本文绝对期待你了解如何进行模运算和素数域的工作,并熟悉多项式、插值和评估的概念。如果你不熟悉这些,请回去阅读 第 2 部分,还有这篇关于二次算术程序的 早期文章。
现在,让我们开始。
MIMC
以下是我们将进行 STARK 的函数:
def mimc(inp, steps, round_constants):
start_time = time.time()
for i in range(steps-1):
inp = (inp**3 + round_constants[i % len(round_constants)]) % modulus
print("MIMC 计算耗时 %.4f 秒" % (time.time() - start_time))
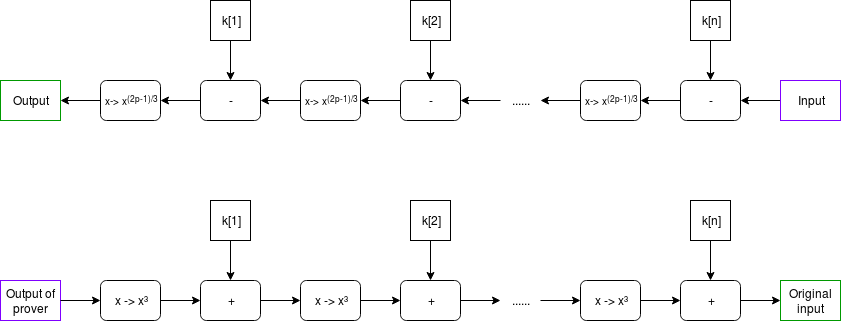
return inp我们选择 MIMC(见 论文)作为示例,因为它既 (i) 容易理解,也 (ii) 有趣到可在现实生活中有所应用。该函数在视觉上可以呈现如下:

在我们的示例中,轮常量将是一个相对较小的列表(例如 64 项),该列表会被循环使用(即在 k[64] 后,它回到使用 k[1])。
MIMC 通过大量轮次如我们这里所做的,作为一种 可验证延迟函数 非常有用 - 一个难以计算、特别是不可并行计算的函数,但相对而言验证却很容易。MIMC 本身在某种程度上就具备这个特性,因为 MIMC 可以 被“反向”计算(恢复对应输出的“输入”),但反向计算所需的时间大约是正向计算的 100 倍(而且,正向和反向计算方向都不能通过并行化显著加快)。所以,你可以将反向计算该函数视为 “计算” 难以并行并且不可并行的工作证明,而正向计算则视为在完成“验证”的过程。
我们要努力实现的目标是通过使用 STARK 来使验证变得更高效 - 验证者不必自己运行 MIMC 的正向计算,证明者在完成反向计算后,将计算 STARK 的过程放在正向计算上,而验证者则只需验证 STARK。我们的希望是计算 STARK 的开销小于运行 MIMC 正向计算和反向计算的速度差,因此证明者的时间仍然主要被初始的“反向”计算支配,而不是(高度并行化的)STARK 计算。STARK 的验证可以相对快速(在我们的 Python 实现中,大约为 0.05-0.3 秒),无论原始计算持续多长时间。
所有的计算都是在模 2256−351⋅232+1 下进行的;我们使用这个素数域模数是因为它是小于 2256 的最大素数,其乘法群包含一个阶为 232 的子群(即,有一个数 g 使得 g 的连续幂模此素数下循环回到 1,正好经过 232 次),并且它是 6k+5 的形式。第一个属性对于确保我们的 FFT 和 FRI 算法的有效版本能够工作是必要的,第二个确保 MIMC 实际上可以进行“反向”计算(请参见上面使用的 x→x(2p−1)/3)。
素数域操作
我们首先构建一个便利类,可以进行素数域操作以及在素数域上进行多项式运算。代码可以在 这里。
首先有一些简单的部分:
class PrimeField():
def __init__(self, modulus):
# 快速素性测试
assert pow(2, modulus, modulus) == 2
self.modulus = modulus
def add(self, x, y):
return (x+y) % self.modulus
def sub(self, x, y):
return (x-y) % self.modulus
def mul(self, x, y):
return (x*y) % self.modulus以及用于计算模逆的 扩展欧几里得算法(相当于在素数域中计算 1/x):
# 使用扩展欧几里得算法进行模逆
def inv(self, a):
if a == 0:
return 0
lm, hm = 1, 0
low, high = a % self.modulus, self.modulus
while low > 1:
r = high//low
nm, new = hm-lm*r, high-low*r
lm, low, hm, high = nm, new, lm, low
return lm % self.modulus上述算法相对耗时;幸运的是,对于我们需要进行多次模逆的特殊情况,有一个简单的数学技巧可让我们计算多个逆,称为 蒙哥马利批量逆:

以下代码实现此算法,包含一些略显晦涩的特殊情况逻辑,以使得如果我们反转的集合中有零,则将其逆设为 0 并继续。
def multi_inv(self, values):
partials = [1]
for i in range(len(values)):
partials.append(self.mul(partials[-1], values[i] or 1))
inv = self.inv(partials[-1])
outputs = [0] * len(values)
for i in range(len(values), 0, -1):
outputs[i-1] = self.mul(partials[i-1], inv) if values[i-1] else 0
inv = self.mul(inv, values[i-1] or 1)
return outputs这个批量逆算法在我们开始处理多项式评价的一组除法时,将变得非常重要。
现在我们进入一些多项式操作。我们将多项式视为一个数组,其中元素 i 是 i 阶项(例如,x3+2x+1 被表示为 [1, 2, 0, 1])。以下是评估多项式在一个点的操作:
# 在一个点上评估多项式
def eval_poly_at(self, p, x):
y = 0
power_of_x = 1
for i, p_coeff in enumerate(p):
y += power_of_x * p_coeff
power_of_x = (power_of_x * x) % self.modulus
return y % self.modulus挑战
如果模数是 31,那么f.eval_poly_at([4, 5, 6], 2)的输出是什么?鼠标悬停以下查看答案
6⋅2²+5⋅2+4=38, 38mod31=7。
还有用于添加、减去、相乘和除法的多项式的代码;这些是教科书中的长加法/减法/乘法/除法。唯一非平凡的事情是拉格朗日插值,它接收一组 x 和 y 坐标,并返回一个最低的多项式,它通过所有这些点(你可以把它看做多项式评估的反向过程):
# 建立一个在所有指定的 x 处返回 0 的多项式
def zpoly(self, xs):
root = [1]
for x in xs:
root.insert(0, 0)
for j in range(len(root)-1):
root[j] -= root[j+1] * x
return [x % self.modulus for x in root]
def lagrange_interp(self, xs, ys):
# 生成主分子多项式,例如 (x - x1) * (x - x2) * ... * (x - xn)
root = self.zpoly(xs)
# 为每个值生成分子多项式,例如对于 x=x2,
# (x - x1) * (x - x3) * ... * (x - xn),通过将主多项式
# 根据每个 x 坐标进行除法
nums = [self.div_polys(root, [-x, 1]) for x in xs]
# 通过在每个 x 处评估分子多项式生成分母
denoms = [self.eval_poly_at(nums[i], xs[i]) for i in range(len(xs))]
invdenoms = self.multi_inv(denoms)
# 生成输出多项式,它是每个分子多项式重标定到正确 y 值后求和的结果
b = [0 for y in ys]
for i in range(len(xs)):
yslice = self.mul(ys[i], invdenoms[i])
for j in range(len(ys)):
if nums[i][j] and ys[i]:
b[j] += nums[i][j] * yslice
return [x % self.modulus for x in b]请参见 这篇文章的 "M of N" 部分 以了解数学的描述。请注意,我们也有特殊情况方法 lagrange_interp_4 和 lagrange_interp_2 以加速频繁的拉格朗日插值操作,特别是对于度数低于 2 和 4 的多项式。
快速傅里叶变换
如果你仔细阅读上述算法,你可能会注意到拉格朗日插值和多点评估(即,在 N 个点上评估一个度数低于 N 的多项式)都需要二次时间来执行,例如,如果进行一千个点的拉格朗日插值,则需要几百万步,而进行一百万个点的拉格朗日插值则需要几万亿步。这是不可接受的高水平低效率,因此我们将使用更高效的算法 - 快速傅里叶变换。
FFT 只需 O(n⋅log(n)) 时间(即,进行 1,000 个点时大约需要 10,000 步,进行 1,000,000 个点时大约需要 2000 万步),虽然它的限制较多;x 坐标必须是某个 单位根 的完整集合,并且此单位根的 阶数 为 N=2k。也就是说,如果有 N 个点,x 坐标必须是某个 p 的连续幂 1,p,p²,p³ ...,其中 p^N=1。该算法可以用于多点评估或插值,只需一个小的参数调整即可。
挑战 找到 337 模下第 16 个单位根,但不是第 8 个单位根。
鼠标悬停以下查看答案
59, 146, 30, 297, 278, 191, 307, 40你可以通过以下代码得到这个列表:[print(x) for x in range(337) if pow(x, 16, 337) == 1 and pow(x, 8, 337) != 1],不过还有一种更聪明的方法适用于更大的模数:首先,确定一个模 337 的单个 原根 (即,不是完全平方),通过查找一个值 x,使得
pow(x, 336 // 2, 337) != 1(这些相对容易找到;一个答案是 5),再取其 (336 / 16)'次方。
以下是算法(略为简化;可以在 这里 查看更优化的东西):
def fft(vals, modulus, root_of_unity):
if len(vals) == 1:
return vals
L = fft(vals[::2], modulus, pow(root_of_unity, 2, modulus))
R = fft(vals[1::2], modulus, pow(root_of_unity, 2, modulus))
o = [0 for i in vals]
for i, (x, y) in enumerate(zip(L, R)):
y_times_root = y*pow(root_of_unity, i, modulus)
o[i] = (x+y_times_root) % modulus
o[i+len(L)] = (x-y_times_root) % modulus
return o
def inv_fft(vals, modulus, root_of_unity):
f = PrimeField(modulus)
# 反向 FFT
invlen = f.inv(len(vals))
return [(x*invlen) % modulus for x in
fft(vals, modulus, f.inv(root_of_unity))]你可以尝试在一些输入上运行它,并检查它是否给出,你使用 eval_poly_at 时,应该得到你期望的答案。例如:
>>> fft.fft([3,1,4,1,5,9,2,6], 337, 85, inv=True)
[46, 169, 29, 149, 126, 262, 140, 93]
>>> f = poly_utils.PrimeField(337)
>>> [f.eval_poly_at([46, 169, 29, 149, 126, 262, 140, 93], f.exp(85, i)) for i in range(8)]
[3, 1, 4, 1, 5, 9, 2, 6]傅里叶变换以 [x[0] .... x[n-1]] 为输入,其目标是输出 x[0] + x[1] + ... + x[n-1] 作为第一个元素,x[0] + x[1] * 2 + ... + x[n-1] * w**(n-1) 作为第二个元素,等等;快速傅里叶变换通过将数据分成两半,分别对两半进行 FFT,然后将结果粘合在一起,从而实现此目的。

我推荐 这篇文档 以获取对 FFT 工作原理或多项式数学的更多直观理解,以及 这个讨论 以获取更多 DFT 与 FFT 的细节,不过要注意,大多数关于傅里叶变换的文献讨论的是实数和复数上的傅里叶变换,而不是素数域上的傅里叶变换。如果你觉得这太难而不想去理解,只需将其视为奇怪的魔法,因为你多次运行代码并验证它有效就可以了。
感谢上帝今天是 FRI 日(那是 “快速 Reed-Solomon 交互式 oracle 近似证明”)
提醒:现在是回顾并重新阅读 第 2 部分的好时机。
现在,我们将获取用于生成低度证明的 代码。回顾一下,低度证明是一个(概率性的)证明,至少有高百分比(例如 80%)的给定值集代表一些特定多项式的评估,该多项式的度数远低于给定值的数量。直观地想象一下,它就是一个证明,“我们所宣称代表多项式的某个 Merkle 根实际上确实代表了一个多项式,可能有一些错误”。作为输入,我们有:
- 一组我们声称是低度多项式评估的值
- 一个单位根;多项式评估的 x 坐标是该单位根的连续幂
- 一个值 N,表明我们要证明多项式的度数是 严格小于 N
- 模数
我们采取的是递归方法,分为两种情况。首先,如果度数足够低,我们可以直接提供整个值列表作为证明;这就是“基本情况”。基本情况的验证是微不足道的:进行一个 FFT 或拉格朗日插值或其它操作来插值代表这些值的多项式,并验证其度数小于 N。否则,如果度数高于某个设定的最小值,我们按照 第 2 部分底部描述的垂直和对角线的方法。
我们首先将值放入 Merkle 树,并使用 Merkle 根选择一个伪随机的 x 坐标(special_x)。然后,我们计算“列”:
# 计算 x 坐标集
xs = get_power_cycle(root_of_unity, modulus)
column = []
for i in range(len(xs)//4):
x_poly = f.lagrange_interp_4(
[xs[i+len(xs)*j//4] for j in range(4)],
[values[i+len(values)*j//4] for j in range(4)],
)
column.append(f.eval_poly_at(x_poly, special_x))这几行代码压缩了很多内容。广泛的思路是将多项式 P(x) 重新解释为多项式 Q(x,y),其中 P(x)=Q(x,x4)。如果 P 的度数 <N,则 P′(y)=Q(special_x,y) 的度数将 <N4。因为我们不想努力将 Q 实际计算为系数形式(那将需要一个仍然相对繁琐且昂贵的 FFT!),我们再使用一个技巧。对于任何给定的值 x4,有 4 个对应的 x 值:x、modulus−x,再加上 x 乘以 −1 的两个模平方根。因此,我们已经有了 4 个值 Q(?,x4),可以用它们去插值多项式 R(x)=Q(x,x4),从而计算 R(special_x)=Q(special_x,x4)=P′(x4)。有 N4 个可能的 x4 值,这使得我们能够轻松计算所有这些值。
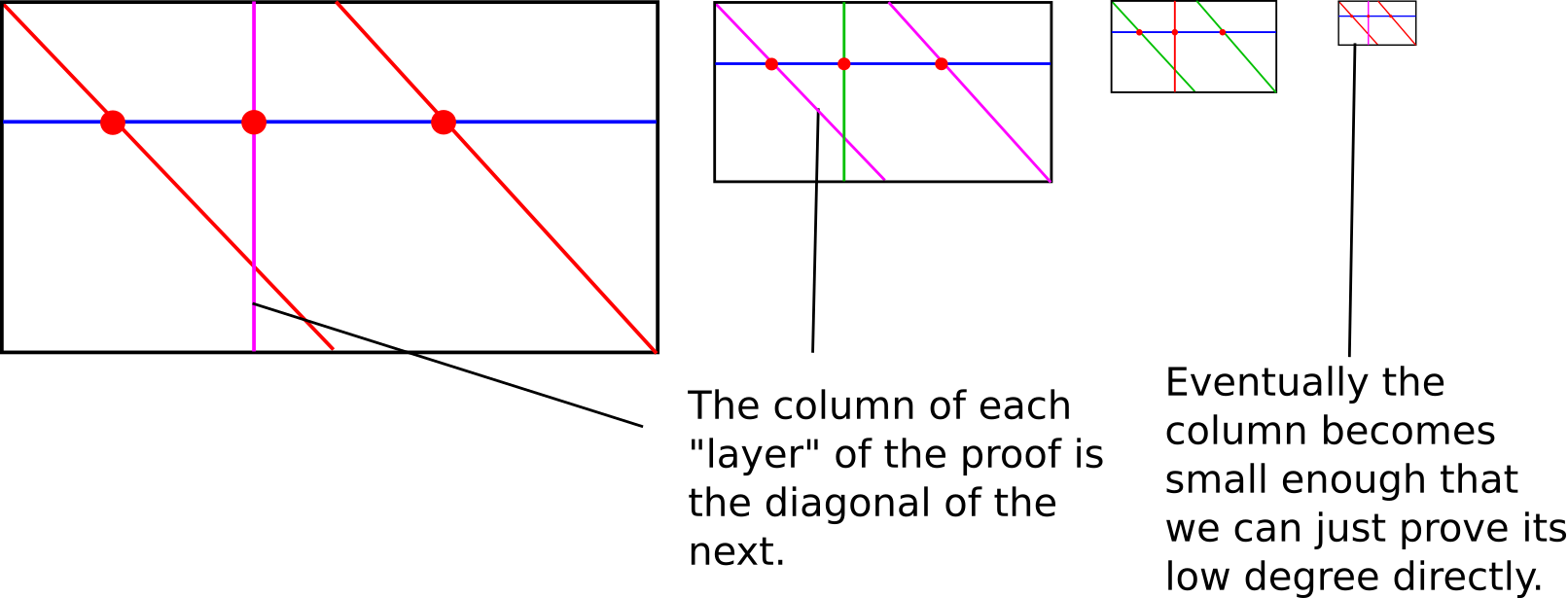 我们的证明由一些随机查询(例如 40 个)组成,这些查询来自于 x4 的值列表(使用该列的 Merkle 根作为种子),对于每个查询,我们提供五个值 Q(?,x4) 的 Merkle 分支:
我们的证明由一些随机查询(例如 40 个)组成,这些查询来自于 x4 的值列表(使用该列的 Merkle 根作为种子),对于每个查询,我们提供五个值 Q(?,x4) 的 Merkle 分支:
m2 = merkelize(column)
# 伪随机选择 y 个索引进行采样
# (m2[1] 是该列的 Merkle 根)
ys = get_pseudorandom_indices(m2[1], len(column), 40)
# 计算多项式中的值和列的 Merkle 分支
branches = []
for y in ys:
branches.append([mk_branch(m2, y)] +
[mk_branch(m, y + (len(xs) // 4) * j) for j in range(4)])验证者的任务将是验证这五个值确实位于同一个度数 <4 的多项式上。然后我们递归地在该列上执行 FRI,验证该列确实具有度数 <N4。这就是 FRI 的全部内容。
作为一个挑战练习,你可以尝试创建具有错误的多项式评估的低度证明,看看你可以让验证者通过多少错误(提示:你需要修改 prove_low_degree 函数;使用默认的证明者,甚至一个错误就会导致验证失败)。
STARK
提示 : 现在可能是查看和重读 第一部分 的好时机
现在,我们进入将所有这些部分结合在一起的实际内容:def mk_mimc_proof(inp, steps, round_constants)(代码 这里),它生成一个运行 MIMC 函数的执行结果证明,给定输入和一些步骤。首先,一些断言:
assert steps <= 2**32 // extension_factor
assert is_a_power_of_2(steps) and is_a_power_of_2(len(round_constants))
assert len(round_constants) < steps扩展因子是我们将扩展计算轨迹的程度(执行 MIMC 函数的“中间值”集合)。我们需要步骤计数乘以扩展因子最多为 232,因为我们没有阶为 2k(k>32)的单位根。
我们的第一步计算是生成计算轨迹;也就是说,从输入到输出的计算的所有 中间 值。
# 生成计算轨迹
computational_trace = [inp]
for i in range(steps-1):
computational_trace.append((computational_trace[-1]**3 + round_constants[i % len(round_constants)]) % modulus)
output = computational_trace[-1]然后我们将计算轨迹转换为多项式,在 successive powers of a root of unity g 处“放置”轨迹中的连续值,其中 gsteps = 1,然后在更大的集合中评估该多项式,successive powers of a root of unity g2 其中 (g2)steps⋅8=1(注意 (g2)8=g)。
computational_trace_polynomial = inv_fft(computational_trace, modulus, subroot)
p_evaluations = fft(computational_trace_polynomial, modulus, root_of_unity)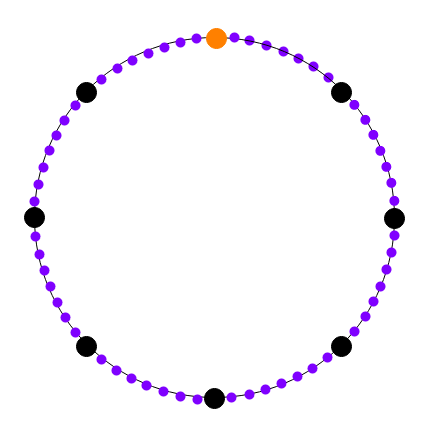
我们可以将 MIMC 的循环常量转换为多项式。因为这些循环常量非常频繁地循环(在我们的测试中,每 64 步),结果表明它们形成一个 Degree-64 的多项式,我们很容易计算出它的表达式及其扩展:
skips2 = steps // len(round_constants)
constants_mini_polynomial = fft(round_constants, modulus, f.exp(subroot, skips2), inv=True)
constants_polynomial = [0 if i % skips2 else constants_mini_polynomial[i//skips2] for i in range(steps)]
constants_mini_extension = fft(constants_mini_polynomial, modulus, f.exp(root_of_unity, skips2))假设有 8192 步执行和 64 个循环常量。这里我们在做什么:我们做一个 FFT 来计算以 (g1)128 为函数的循环常量。然后我们在常量之间添加零,使其成为 g1 本身的函数。因为 (g1)128 每 64 步循环一遍,我们知道这个 g1 的函数也会如此。我们只计算扩展的 512 步,因为我们知道扩展也在 512 步后重复。
我们现在像第一部分的斐波那契示例一样计算 C(P(x)),只不过这次是 C(P(x),P(g1⋅x),K(x)):
# 创建复合多项式,使得
# C(P(x), P(g1*x), K(x)) = P(g1*x) - P(x)**3 - K(x)
c_of_p_evaluations = [(p_evaluations[(i+extension_factor)%precision] -
f.exp(p_evaluations[i], 3) -
constants_mini_extension[i % len(constants_mini_extension)])
% modulus for i in range(precision)]
print('计算出 C(P, K) 多项式')请注意,我们不再使用 系数形式 下的多项式;我们以多少顺序的高次单位根的评估形式来处理这些多项式。
c_of_p 的目标是 Q(x)=C(P(x),P(g1⋅x),K(x))=P(g1⋅x)−P(x)3−K(x);目标是对于每个我们在该计算轨迹中放下的 x(除了最后一步,因为最后一步后没有“下一步”),轨迹中的下一个值等于轨迹中前一个值的立方,加上循环常量。与第一部分中的斐波那契示例不同,如果一个计算步骤在坐标 k 处,则下一个步骤在坐标 k+1 处,这里我们在较低次单位根 g1 的连续幂中放置计算轨迹,因此如果一个计算步骤位于 x=(g1)i,下一步位于 (g1)i+1 = (g1)i⋅g1=x⋅g1。因此,除了最后一个低阶单位根 g1 的每一幂中,我们希望 P(x⋅g1)=P(x)3+K(x),或 P(x⋅g1)−P(x)3−K(x)=Q(x)=0。这使得 Q(x) 在所有连续的低阶单位根的幂下(除了最后一个)等于零。
有一个代数定理证明如果 Q(x) 在所有这些 x 坐标上均为零,那么它是 最小 多项式的倍数,在所有这些 x 坐标上均等于零: Z(x)=(x−x1)⋅(x−x2)⋅...⋅(x−xn)。由于证明 Q(x) 在我们要检查的每个坐标上等于零太难(验证这样的证明所需的时间可能比运行原始计算还要长!),因此我们使用一种间接方法(概率性)证明 Q(x) 是 Z(x) 的倍数。那么我们如何做到这一点?通过提供商 D(x)=Q(x)/Z(x) 并使用 FRI 来证明这实际上是一个多项式,而不是一个分数,当然!
我们选择了较低阶和较高阶单位根的特定排列(而不是,例如在高阶单位根的前几个幂中放置计算轨迹),因为计算 Z(x)(在计算跟踪中除最后一个外的所有点上评估为零的多项式)很简单,在那里除以 Z(x) 也是微不足道的:Z 的表达式是两个项的分式。
# 计算 D(x) = Q(x) / Z(x)
# Z(x) = (x^steps - 1) / (x - x_atlast_step)
z_num_evaluations = [xs[(i * steps) % precision] - 1 for i in range(precision)]
z_num_inv = f.multi_inv(z_num_evaluations)
z_den_evaluations = [xs[i] - last_step_position for i in range(precision)]
d_evaluations = [cp * zd * zni % modulus for cp, zd, zni in zip(c_of_p_evaluations, z_den_evaluations, z_num_inv)]
print('计算出 D 多项式')请注意,我们直接以“评估形式”计算 Z 的分子和分母,然后使用批量模逆转换将除以 Z 变为乘法(⋅zd⋅zni),然后逐项乘以 Q(x) 的评估与这些 Z(x) 的逆。请注意,在除了最后一个低阶根的幂(即原始计算轨迹的一部分的低级扩展部分)中,Z(x)=0,因此涉及其逆的此计算将失败。这是一个不幸的情况,尽管我们将通过简单地修改随机检查和 FRI 算法来避免在这些点采样,因此我们计算错误的事实将无关紧要。
由于 Z(x) 可以如此紧凑地表达,因此我们还有另一个好处:验证者可以对任何特定的 x 以极快的速度计算 Z(x),而无需任何预计算。让 证明者 处理其大小等于步骤数的多项式是可以的,但我们不希望要求 验证者 这样做,因为我们希望验证是简洁的(即超快,证明尽可能小)。
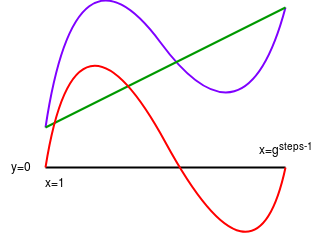
以概率方式检查 D(x)⋅Z(x)=Q(x) 在一些随机选择的点上允许我们验证 过渡约束 - 每一步计算是前一步的有效结果。但我们还想验证 边界约束 - 输入和计算的输出即证明者所说的。如果只是让证明者提供 P(1)、D(1)、P(last_step) 和 D(last_step)(其中 last_step (或 gsteps−1) 是对应于计算最后一步的坐标)太脆弱;这没有证明这些值与其余数据在同一多项式上。因此,我们使用一种类似的多项式除法技巧:
# 计算 ((1, input), (x_atlast_step, output)) 的插值
interpolant = f.lagrange_interp_2([1, last_step_position], [inp, output])
i_evaluations = [f.eval_poly_at(interpolant, x) for x in xs]
zeropoly2 = f.mul_polys([-1, 1], [-last_step_position, 1])
inv_z2_evaluations = f.multi_inv([f.eval_poly_at(quotient, x) for x in xs])
# B = (P - I) / Z2
b_evaluations = [((p - i) * invq) % modulus for p, i, invq in zip(p_evaluations, i_evaluations, inv_z2_evaluations)]
[](7-10)print('计算出 B 多项式')论点如下。证明者想要证明 P(1)=input 和 P(last_step)=output。如果我们将 I(x) 视为 插值 - 通过两点 (1,input) 和 (last_step,output) 的直线,那么 P(x)−I(x) 在这两点处将等于零。因此,证明 P(x)−I(x) 是 (x−1)⋅(x−last_step) 的倍数便足够了,我们通过...提供商来实现这一目标!
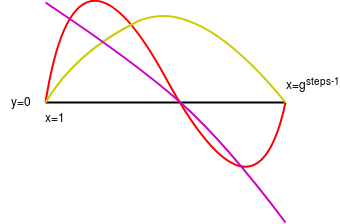
挑战 如果你还想证明计算轨迹在第 703 步之后的值等于 8018284612598740。你将如何修改上述算法以做到这一点?
鼠标悬停以查看答案
将 I(x) 设置为 (1,input),(g703,8018284612598740),(last_step,output) 的插值,并通过提供商 B(x)=P(x)−I(x)(x−1)⋅(x−g703)⋅(x−last_step) 来证明。
现在,我们提交 P、D 和 B 的 Merkle 根的组合。
# 计算它们的 Merkle 根
mtree = merkelize([pval.to_bytes(32, 'big') +
dval.to_bytes(32, 'big') +
bval.to_bytes(32, 'big') for
pval, dval, bval in zip(p_evaluations, d_evaluations, b_evaluations)])
print('计算出哈希根')现在,我们需要证明 P、D 和 B 实际都是多项式,并且具有正确的最大度数。但是 FRI 证明又大又昂贵,我们不希望有三个 FRI 证明。因此,我们计算 P、D 和 B 的伪随机线性组合(使用 P、D 和 B 的 Merkle 根作为种子),并对其进行 FRI 证明:
k1 = int.from_bytes(blake(mtree[1] + b'\x01'), 'big')
k2 = int.from_bytes(blake(mtree[1] + b'\x02'), 'big')
k3 = int.from_bytes(blake(mtree[1] + b'\x03'), 'big')
k4 = int.from_bytes(blake(mtree[1] + b'\x04'), 'big')
# 计算线性组合。我们甚至不去计算它
# 在系数形式中;我们只计算评估
root_of_unity_to_the_steps = f.exp(root_of_unity, steps)
powers = [1]
[](9-10)for i in range(1, precision):
[](9-11) powers.append(powers[-1] * root_of_unity_to_the_steps % modulus)
[](9-12)
[](9-13)l_evaluations = [(d_evaluations[i] +
[](9-14) p_evaluations[i] * k1 + p_evaluations[i] * k2 * powers[i] +
[](9-15) b_evaluations[i] * k3 + b_evaluations[i] * powers[i] * k4) % modulus
[](9-16) for i in range(precision)]除非全部三个多项式具有正确的低度,否则几乎不可能选取它们的随机线性组合(你必须 极端 幸运,才能使项相消),所以这是足够的。
我们想证明 D 的度小于 2⋅steps,并且 P 和 B 的度小于 steps,因此我们实际上随机线性组合 P、P⋅xsteps、B、Bsteps 及 D,检查该组合的度小于 2⋅steps。
现在,我们对所有多项式进行一些抽查。我们生成一些随机索引,并提供在这些索引处评估的多项式的 Merkle 分支:
# 对伪随机坐标的 Merkle 树进行一些抽查,排除
# `extension_factor` 的倍数
branches = []
samples = spot_check_security_factor
positions = get_pseudorandom_indices(l_mtree[1], precision, samples,
exclude_multiples_of=extension_factor)
for pos in positions:
branches.append(mk_branch(mtree, pos))
branches.append(mk_branch(mtree, (pos + skips) % precision))
branches.append(mk_branch(l_mtree, pos))
print('计算出 %d 次抽查' % samples)get_pseudorandom_indices 函数返回[0...precision-1] 范围内的一些随机索引,exclude_multiples_of 参数告知其不返回是给定参数(此处为 extension_factor)的倍数。这确保我们不会在原始计算轨迹上进行采样,我们可能会得出错误的答案。
证明(约 250-500 KB)由一组 Merkle 根、抽查的分支和随机线性组合的低度证明组成:
o = [mtree[1],
l_mtree[1],
branches,
prove_low_degree(l_evaluations, root_of_unity, steps * 2, modulus, exclude_multiples_of=extension_factor)]在实践中,证明的最大部分是 Merkle 分支和 FRI 证明,后者由更多分支组成。而且验证者的“核心”部分是:
for i, pos in enumerate(positions):
x = f.exp(G2, pos)
x_to_the_steps = f.exp(x, steps)
mbranch1 = verify_branch(m_root, pos, branches[i*3])
mbranch2 = verify_branch(m_root, (pos+skips)%precision, branches[i*3+1])
l_of_x = verify_branch(l_root, pos, branches[i*3 + 2], output_as_int=True)
p_of_x = int.from_bytes(mbranch1[:32], 'big')
p_of_g1x = int.from_bytes(mbranch2[:32], 'big')
d_of_x = int.from_bytes(mbranch1[32:64], 'big')
b_of_x = int.from_bytes(mbranch1[64:], 'big')
zvalue = f.div(f.exp(x, steps) - 1,
x - last_step_position)
k_of_x = f.eval_poly_at(constants_mini_polynomial, f.exp(x, skips2))
# 检查过渡约束 Q(x) = Z(x) * D(x)
assert (p_of_g1x - p_of_x ** 3 - k_of_x - zvalue * d_of_x) % modulus == 0
# 检查边界约束 B(x) * Z2(x) + I(x) = P(x)
interpolant = f.lagrange_interp_2([1, last_step_position], [inp, output])
zeropoly2 = f.mul_polys([-1, 1], [-last_step_position, 1])
assert (p_of_x - b_of_x * f.eval_poly_at(zeropoly2, x) -
f.eval_poly_at(interpolant, x)) % modulus == 0
# 检查线性组合的正确性
assert (l_of_x - d_of_x -
k1 * p_of_x - k2 * p_of_x * x_to_the_steps -
k3 * b_of_x - k4 * b_of_x * x_to_the_steps) % modulus == 0在证明者为每个提供 Merkle 证明的位置,验证者检查 Merkle 证明,并检查 C(P(x),P(g1⋅x),K(x))=Z(x)⋅D(x) 以及 B(x)⋅Z2(x)+I(x)=P(x)(提醒:对于不沿着原始计算轨迹的 x,Z(x) 不为零,因此 C(P(x),P(g1⋅x),K(x)) 可能不会评估为零)。验证者还会检查线性组合是否正确,并调用 verify_low_degree_proof(l_root, root_of_unity, fri_proof, steps * 2, modulus, exclude_multiples_of=extension_factor) 验证 FRI 证明。我们完成了!
其实并非如此;声音分析以证明交叉多项式检查和 FRI 所需的检查次数非常棘手。但是这就是代码的全部内容,至少如果你不关心做更疯狂的优化。当我运行上述代码时,我们得到 STARK 证明“开销”约为 300-400 倍(例如,计算 MIMC 需要 0.2 秒的计算需要 60 秒进行证明),这表明,在一个四核机器上,以前向方式计算 MIMC 计算的 STARK 可能实际上比以反向方式计算 MIMC 更快。尽管如此,这两种方法在 Python 中都是相对低效的实现,因此优化良好的实现的证明与运行时间的比率可能会有所不同。此外,值得指出的是,MIMC 的 STARK 证明开销是相当低的,因为 MIMC 几乎是完全“可算数的”——它的数学形式非常简单。对于“普通”计算,其中包含较少的算术干净操作(例如,检查某个数字是否大于或小于另一个数字),开销可能会高得多,可能在 10000-50000 倍之间。
- 原文链接: vitalik.eth.limo/general...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- ZK编年史:哈希登场 117 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 331 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 277 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 353 浏览
- Zcash:比特币遗忘的隐私 428 浏览
- ZK编年史:计算模型 294 浏览
- lambdaworks 2026 年更新路线图和优先级 351 浏览
- 2026年构建机构级DeFi平台真正需要什么 880 浏览
- zkMesh:2026年1月回顾 443 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 635 浏览
- Zcash 的时代到来了 756 浏览
- ZK 编年史:电路(第二部分) 418 浏览

