快速傅里叶变换

快速傅里叶变换

触发警告：专业数学主题

特别感谢 Karl Floersch 的反馈

在数论中，其中一个更有趣的算法是快速傅里叶变换（FFT）。FFT 是许多算法中的关键构建块，包括大数的极快乘法、多项式的乘法以及极快生成和恢复纠删码。尤其是纠删码非常灵活；除了在容错数据存储和恢复中的基本用例外，纠删码在确保可扩展区块链中的数据可用性和STARKs等更高级用例中也发挥重要作用。本文将讨论快速傅里叶变换是什么，以及一些更简单的计算算法是如何工作的。

背景

原始的傅里叶变换是一个数学运算，通常被描述为将数据从“频率域”转换到“时间域”。更精确地说，如果你有一段数据，那么运行该算法就会生成一组具有不同频率和振幅的正弦波，若将它们相加，将近似于原始数据。傅里叶变换可以用于表达诸如通过附加圆轨道绘制平方轨道和推导出一个绘制大象的方程组等神奇的事情：

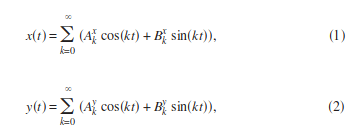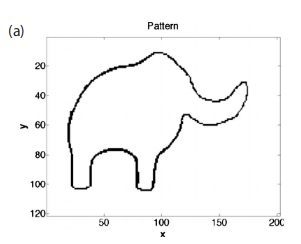运行傅里叶变换算法的“逆”方向只是简单地将正弦波相加并计算所需的值，在你希望采样的任意多个点上。

我们在本文中讨论的傅里叶变换是一种类似的算法，只是它并不是在_实数或复数_上的_连续傅里叶变换，而是 离散傅里叶变换_ 在_有限域_上（见“模块数学插曲”部分这里回顾有限域是什么）。在这里我们不再谈论在“频率域”和“时间域”之间的转换，而是两个不同的操作：多点多项式评估（在 N 个不同点上评估一个度 <N 的多项式）和它的逆操作多项式插值（给定在 N 个不同点上的度 <N 的多项式评估，恢复该多项式）。例如，在模 5 的素数域中，多项式 ²y=x²+3（为了方便，我们可以按递增顺序写出系数：[3,0,1]）在点 [0,1,2] 处的评估结果为 [3,4,2]（而不是 [3,4,7]，因为我们在一个模 5 的有限域中运算），我们实际上可以取评估结果 [3,4,2] 和它们的评估坐标（[0,1,2]），从而恢复原始多项式 [3,0,1]。

对于多点评估和插值都有可以在 O(N²) 时间内完成的算法。多点评估很简单：只需分别在每个点上评估多项式。以下是用于实现的 Python 代码：

def eval_poly_at(self, poly, x, modulus):
    y = 0
    power_of_x = 1
    for coefficient in poly:
        y += power_of_x * coefficient
        power_of_x *= x
    return y % modulus

该算法运行一个循环，遍历每个系数，并针对每个系数执行一项操作，因此它的运行时间为 O(N)。多点评估需要在 N 个不同的点上进行评估，因此总运行时间为 O(N²)。

拉格朗日插值则更为复杂（在这里搜索“拉格朗日插值”可获得更详细的解释）。基本策略的关键构建块是，对于任何域 D 和点 x，我们可以构造一个在 x 处返回 1、在 D 中其他任何值处返回 0 的多项式。例如，如果 D=[1,2,3,4] 和 x=1，那么多项式为：

y=(x−2)(x−3)(x−4)/(1−2)(1−3)(1−4)

你可以心算将 1、2、3 和 4 代入上述表达式，验证它在 x=1 时返回 1，而在其他三个情况下返回 0。

我们可以通过相乘和相加这些多项式来恢复任何期望的输出在给定域上的多项式。如果我们称上述多项式为 P1，对于 x=2、x=3、x=4，称其为 P2、P3 和 P4，那么在域 [1,2,3,4] 上返回 [3,1,4,1] 的多项式就是 3⋅P1+P2+4⋅P3+P4。计算 Pi 多项式需要 O(N²) 时间（你首先构建在整个域上返回 0 的多项式，这需要 O(N²) 时间，然后对于每个 xi 单独除以 (x−xi)），计算线性组合再需 O(N²) 时间，因此总运行时间为 O(N²)。

快速傅里叶变换使得多点评估和插值更快。

快速傅里叶变换

使用这种更快算法需要付出代价，即不能选择任意的有限域和任意的域。相比于拉格朗日插值，可以选择任何的 x 坐标和 y 坐标，和任意的域（甚至可以直接使用实数），并且可以得到通过它们的多项式，而 FFT 要求使用有限域，并且域必须是一个乘法子群（也就是说，一部分某个“生成器”值的幂的列表）。例如，可以使用模 337 的整数有限域，域可选择 [1,85,148,111,336,252,189,226]（这是在该域中 85 的幂，例如 853 % 337=111；因下一个 85 的幂循环返回到 1，所以停止在 226）。此外，乘法子群的大小必须为 2n（存在一些方法使其适用于形式为 2m⋅3n 和可能稍微更高的素数幂的数，但这样会变得更加复杂且低效）。模 59 的整数有限域就不适用，因为只有大小为 2、29 和 58 的乘法子群；2 太小，不具趣味性，因子 29 又太大，不能让一般的 FFT 操作变得友好。乘法群的对称性，可以让我们创建递归算法，从较少的工作中巧妙地计算出我们想要的结果。

为了理解这个算法及其为何有较低的运行时间，理解递归的一般概念是很重要的。递归算法是具有两个情况的算法：“基础情况”，即输入小到可以直接给出输出，和“递归情况”，即所需的计算由一些“结合计算”加上一种或多种对较小输入使用相同算法的形式。例如，你可能看到递归算法用于排序。假设你有一个列表（例如：[1,8,7,4,5,6,3,2,9]），可以用以下过程对它进行排序：

• 如果输入只有一个元素，则它已经“排序”，所以你可以直接返回该输入。
• 如果输入有多个元素，则将列表的前半部分和后半部分各自进行排序，然后将两个排序好的子列表（称为 A 和 B）合并，如下所示。维持两个计数器 apos 和 bpos，两者均从零开始，同时维持一个空的输出列表。直到 apos 或 bpos 的某一者到达相应列表的末尾，检查 A[apos] 或 B[bpos] 是否更小。将较小的值添加到输出列表的末尾，并将该计数器增加 1。一旦完成，将任何尚未完全处理的列表的其余部分添加到输出列表的末尾，然后返回输出列表。

注意，第二个过程中的“结合”运行时间为 O(N)：如果两个子列表各有 N 个元素，则必须遍历每个列表中的每个条目一次，因此总计算时间为 O(N)。因此，整个算法通过将一个大小为 N 的问题分解为两个大小为 N/2 的子问题，加上 O(N) 的“结合”执行，总时间复杂度为 O(N⋅log(N))。

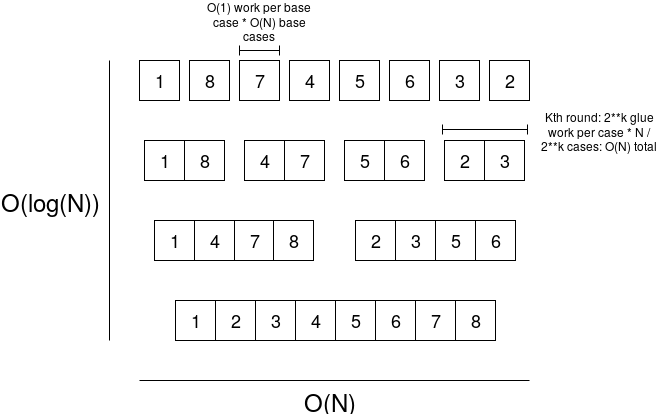
FFT 也是这么工作的。我们将一个大小为 N 的问题拆分成两个大小为 N/2 的子问题，然后做 O(N) 的结合工作，将较小的解决方案合并为较大的解决方案，因此总运行时间为 O(N⋅log(N)) - 比 O(N²) 快得多。具体我们是如何做到的。首先介绍如何使用 FFT 进行多点评估（即，对于某个域 D 和多项式 P，计算 D 中每个 x 的 P(x)），并发现可以使用相同的算法进行插值，只需稍作调整。

假设我们有一个 FFT，其中给定的域是某个域中 x 的幂，x²k=1（例如在我们以上介绍的案例中，域是模 337 的 85 的幂，并且 8523=1）。我们有某个多项式，例如 y=6x7+2x6+9x5+5x4+x3+4x2+x+3（我们将其表示为 p=[3,1,4,1,5,9,2,6]）。我们想要在该域内的每个值上评估这个多项式，即在八个 85 的幂上评估。我们需要这样做。首先，我们将该多项式分为两部分，分别称之为偶数系数和奇数系数：evens=[3,4,5,2] 和 odds=[1,1,9,6]（或 evens=2x3+5x2+4x+3 和 odds=6x3+9x2+x+1；是的，这只是将偶数次系数和奇数次系数分开）。现在，注意一个数学观察： p(x)=evens(x²)+x⋅odds(x²) 和 p(−x)=evens(x²)−x⋅odds(x²)（思考一下这个并确保你理解它，然后再继续）。

在这里，我们有一个很好的特性：evens 和 odds 都是 p 的一半大小的多项式，并且数据的 x² 值只有原域的一半大小，因为存在一对一的对应关系：x 和 −x 都在 D 中（例如在当前的域 [1,85,148,111,336,252,189,226]，1 和 336 是彼此的相反数，因为 336=−1 % 337，而按逆也是如此(85,252), (148,189) 和 (111,226)。x 和 −x 始终具有相同的平方。因此，我们可以使用 FFT 计算在原域的数字的平方组成的小型域（[1,148,336,189]）中 evens(x) 的结果，也可以对 odds 执行相应操作。为了这样做，我们就将一个大小为 N 的问题减小为两个部分大小的问题。

"结合"工作相对容易（并且 O(N) 时间）：我们以大小为 N 的列表的形式接收偶数和奇数的评估结果，因此我们简单地执行 p[i]=evens_result[i]+domain[i]⋅odds_result[i] 和 p[N/2+i]=evens_result[i]−domain[i]⋅odds_result[i]。

以下是完整的代码：

def fft(vals, modulus, domain):
    if len(vals) == 1:
        return vals
    L = fft(vals[::2], modulus, domain[::2])
    R = fft(vals[1::2], modulus, domain[::2])
    o = [0 for i in vals]
    for i, (x, y) in enumerate(zip(L, R)):
        y_times_root = y*domain[i]
        o[i] = (x+y_times_root) % modulus
        o[i+len(L)] = (x-y_times_root) % modulus
    return o

我们可以尝试运行它：

>>> fft([3,1,4,1,5,9,2,6], 337, [1, 85, 148, 111, 336, 252, 189, 226])
[31, 70, 109, 74, 334, 181, 232, 4]

然后我们可以检查结果；例如，在 85 的位置评估多项式实际上确实给出了结果 70。请注意，这仅在“域是正确的”情况下工作；它的结构必须是[xi % modulus for i in range(n)]且 xn=1。

逆 FFT 令人惊讶的简单：

def inverse_fft(vals, modulus, domain):
    vals = fft(vals, modulus, domain)
    return [x * modular_inverse(len(vals), modulus) % modulus for x in [vals[0]] + vals[1:][::-1]]

基本上，再次运行 FFT，但逆转结果（除了第一个项保持不变)并除以列表的长度。

>>> domain = [1, 85, 148, 111, 336, 252, 189, 226]
>>> def modular_inverse(x, n): return pow(x, n - 2, n)
>>> values = fft([3,1,4,1,5,9,2,6], 337, domain)
>>> values
[31, 70, 109, 74, 334, 181, 232, 4]
>>> inverse_fft(values, 337, domain)
[3, 1, 4, 1, 5, 9, 2, 6]

那么，我们可以用这些做什么呢？以下是一个有趣的用例：我们可以使用 FFT 快速乘法。例如，我们想乘 1253 和 1895。我们要做的第一件事是将问题转换为一个略显简单的问题：将多项式 [3,5,2,1] 和 [5,9,8,1] 相乘（这只是两个数字的位数按升序排列），然后通过单次操作将答案转换回数字。我们可以通过 FFT 快速地乘多项式，因为事实证明，如果将多项式转换为评估形式（即对于某个域 D 中的每个 x，得到 f(x) 的值），则可以通过直接乘以它们的评估结果来乘以两个多项式。所以我们将把表示我们两个数字的多项式转变为系数形式，使用 FFT 将它们转换为评估形式，按点乘法，然后再转换回：

>>> p1 = [3,5,2,1,0,0,0,0]
>>> p2 = [5,9,8,1,0,0,0,0]
>>> x1 = fft(p1, 337, domain)
>>> x1
[11, 161, 256, 10, 336, 100, 83, 78]
>>> x2 = fft(p2, 337, domain)
>>> x2
[23, 43, 170, 242, 3, 313, 161, 96]
>>> x3 = [(v1 * v2) % 337 for v1, v2 in zip(x1, x2)]
>>> x3
[253, 183, 47, 61, 334, 296, 220, 74]
>>> inverse_fft(x3, 337, domain)
[15, 52, 79, 66, 30, 10, 1, 0]

这需要三次 FFT（每次 O(N⋅log(N)) 时间）和一次点乘（O(N) 时间），因此总时间为 O(N⋅log(N))（严格来说，可能超过 O(N⋅log(N))，因为对于非常大的数字，你需要使用更大的模数，而这会使乘法变得更加困难，但也不算太离谱）。这比学校书上乘法所需的 O(N²) 时间快得多：

         3  5  2  1
       ------------
    5 | 15 25 10  5
    9 |    27 45 18  9
    8 |       24 40 16  8
    1 |           3  5  2  1
       ---------------------
        15 52 79 66 30 10  1

现在我们只需获取结果，并进位（这是一个“遍历列表一次并在每个点上做一件事情”的算法，所以它需要 O(N) 的时间）：

[15, 52, 79, 66, 30, 10, 1, 0]
[ 5, 53, 79, 66, 30, 10, 1, 0]
[ 5,  3, 84, 66, 30, 10, 1, 0]
[ 5,  3,  4, 74, 30, 10, 1, 0]
[ 5,  3,  4,  4, 37, 10, 1, 0]
[ 5,  3,  4,  4,  7, 13, 1, 0]
[ 5,  3,  4,  4,  7,  3, 2, 0]

如果我们从上到下读取这些数字，我们得到 2374435。让我们检查答案：

>>> 1253 * 1895
2374435

太好了！成功了。实际上，在如此小的输入下，O(N⋅log(N)) 和 O(N²) 之间的差别并不是_太_大，因此学校书上的乘法由于其算法更简单，反而比这个基于 FFT 的乘法速度更快，但是在大的输入上，性能差异则非常显著。

但是 FFT 不仅在乘法上有用；如上所述，多项式乘法和多点评估在执行纠删编码中至关重要，而这是一种构建许多种类冗余容错系统的非常重要的技术。如果你喜欢容错性和效率，FFT 是你的朋友。

FFTs 和二进制域

素数域并不是唯一的有限域。另一种有限域（实际上是更一般的_扩展域_的特殊情况，类似于有限域的复数）是二进制域。在二进制域中，每个元素都表示为一个所有条目为 0 或 1 的多项式，例如 x³+x+1。对多项式的加法按模 2 进行，而减法与加法相同（因为 -1=1 mod 2）。我们选择一些不可约多项式作为模数（例如 x⁴+x+1；x⁴+1 不适用，因为 x⁴+1 可以分解成 (x²+1)⋅(x²+1)，因此不是“不可约的”）；乘法按该模数进行。例如，在模 x⁴+x+1 的二进制域中，将 x²+1 乘以 x³+1 ，如果仅仅进行相乘，将得到 x⁵+x³+x²+1，但 x⁵+x³+x²+1=(x⁴+x+1)⋅x+(x³+x+1)，因此结果为余数 x³+x+1。

我们可以将此示例表示为乘法表。首先将 [1,0,0,1]（即 x³+1 ）与 [1,0,1]（即 x²+1）相乘：

        1 0 0 1
       --------
    1 | 1 0 0 1
    0 |   0 0 0 0
    1 |     1 0 0 1
       ------------
        1 0 1 1 0 1

乘法结果包含一个 x⁵ 项，因此我们可以减去 (x⁴+x+1)⋅x：

        1 0 1 1 0 1
      -   1 1 0 0 1    [(x⁴ + x + 1) 向右移位是为了反映乘以 x]
       ------------
        1 1 0 1 0 0

我们得到了结果 [1,1,0,1]（或 x³+x+1）。

二进制域有两个有趣的原因。首先，如果你想对二进制数据进行纠删编码，那么二进制域就非常方便，因为 N 字节的数据可以直接编码为一个二进制域元素，并且通过对其进行计算生成的任何二进制域元素也将具有 N 字节的长度。由于素数域的大小并不恰好是2的幂，你无法做到这一点；例如，可以将每两个字节编码为一个从 0...65536 的数字，模 65537（这是素数），但是如果你对此值进行 FFT，则输出可能会包含 65536，而这不能在两个字节中表示。第二，加法和减法变为相同操作、1+1=0，形成了一些“结构”，从而导致了一些很有趣的后果。一个特别有趣和有用的二进制域特性是“新手梦”定理：（x+y)²=x²+y²（以及相同的情况适用于 4、8、16 等...基本上是任何 2 的幂）。

如果你想快速有效地在二进制域中执行纠删编码，那么你需要能够在二进制域上执行快速傅里叶变换。但是这存在一个问题：在二进制域中，没有（非平凡的）阶为 2n 的乘法群。因为乘法群的阶都是 2n-1。例如，在模 x⁴+x+1 的二进制域中，如果你开始计算 (x+1) 的连续幂，则在 15 步之后会循环回到 1，而不是 16。原因是，该域中的元素总数是 16，但其中之一是零，你永远不会通过将任何非零值与自身相乘来得到零，因此 (x+1) 的幂会循环遍历每个元素，但零被排除掉，因此循环长度是 15，而不是 16。那么我们该怎么做呢？

我们原本需要域具备“结构”，在里面存在 2n 大小的乘法群，是因为我们需要使得通过平方每个数字将域的大小减半：原域 [1,85,148,111,336,252,189,226] 减小为 [1,148,336,189] 的原因是 1 是 1 和 336 的平方；148 是 85 和 252 的平方，等等。但是，如果在二进制域中，有另一种方式使域大小减半？结果证实确实如此：给定一个包含 2k 个元素的域，包含零（技术上讲，该域必须是_子空间_），我们可以通过使用某个特定 k 在 D 中，取 x⋅(x+k) 来构造一个新的半大小域 D'。因为原域是一个子空间，既然 k 在该域内，域中的任何 x 都有相应的 x+k 也在域内，因此函数 f(x)=x⋅(x+k) 在 x 和 x+k 上返回相同的值，从而得到与平方对应的一样的二对一关系。

现在，我们如何在此基础上执行 FFT？我们将使用与之前相同的技巧，将一个 N 大小的多项式和 N 大小的域转换成两个 N/2 大小的多项式和 N/2 大小的域，但这次使用了不同的方程。我们将一个多项式 p 转换为两个多项式偶数和奇数，使得 p(x)=evens(x⋅(k−x))+x⋅odds(x⋅(k−x))。注意，对于我们找到的偶数和奇数，p(x+k)=evens(x⋅(k−x))+(x+k)⋅odds(x⋅(k−x)) 这也将成立。因此我们接下来再对减少的域 [x⋅(k−x) for x in D] 分别应用 FFT 到偶数和奇数，然后利用这两个公式为两个偏移量的 “半”域提供答案。

将 p 转换为按上述描述的偶数和奇数类推复杂，“天真的”算法本身是 O(N²)，但是在二进制域中，可以利用 (x²−kx)²=x⁴−k²・x² 的性质，以及更一般的 (x²−kx)²i=x²i+1−k²i・x²i 的性质，创建另一个递归算法，以 O(N⋅log(N)) 的时间来解决这个问题。

如果你还想执行一个逆 FFT，以进行插值操作，那么需要反向执行算法中的这些步骤。关于此完整实现的代码可以在这里找到：<https://github.com/ethereum/research/tree/master/binary_fft>，更优化算法的详细论文可以在这里找到：&lt;http://www.math.clemson.edu/~sgao/papers/GM10.pdf>

那么，我们从这一切复杂性中得到了什么呢？我们可以尝试执行实现，其中既有“天真的” O(N²) 多点评估，也可以采用基于 FFT 的优化实现，并对两者进行计时。以下是我的结果：

>>> import binary_fft as b
>>> import time, random
>>> f = b.BinaryField(1033)
>>> poly = [random.randrange(1024) for i in range(1024)]
>>> a = time.time(); x1 = b._simple_ft(f, poly); time.time() - a
0.5752472877502441
>>> a = time.time(); x2 = b.fft(f, poly, list(range(1024))); time.time() - a
0.03820443153381348

随着多项式大小的增加，天真实现 (_simple_ft) 的运行速度比 FFT 更快地降速：

>>> f = b.BinaryField(2053)
>>> poly = [random.randrange(2048) for i in range(2048)]
>>> a = time.time(); x1 = b._simple_ft(f, poly); time.time() - a
2.2243144512176514
>>> a = time.time(); x2 = b.fft(f, poly, list(range(2048))); time.time() - a
0.07896280288696289
```而且 voilà，我们已经有了一种高效、可扩展的方法来进行多点评估和插值多项式。如果我们想使用 FFT 来恢复丢失的容量编码数据，那么这个算法也 [存在](https://ethresear.ch/t/reed-solomon-erasure-code-recovery-in-n-log-2-n-time-with-ffts/3039)，尽管它们的效率稍逊于单纯进行一次 FFT。祝好运！

>- 原文链接： [vitalik.eth.limo/general...](https://vitalik.eth.limo/general/2019/05/12/fft.html)
>- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～