区块链中的数学-用Miller Rabin算法判断大素数实例
- blocksight
- 发布于 2020-09-07 18:47
- 阅读 5394
本节从"凭证"的角度来扩展说明了Miller Rabin算法
写在前面
上一节说了抽象的椭圆曲线密钥协商和素数判断法, 对于Miller Rabin素数判定法做了简要的概述, 本文再展开说明一下,并附带具体实现如果篇幅允许的话。
Miller Rabin算法之凭证
结合上一文的说明,该算法利用费马小定理和二次探测定理的逆否性质:
把$p-1$分解为$ 2^k t $ 的形式,即:$ p-1=2^k t$
如果我们能找到这样一个a,使得对任意 0 < r < = k, 以下两个式子均满足:
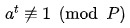
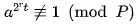
那么p肯定就不是一个素数。这样的a称为p是合数的一个凭证(witness),否则a可能是一个证明p是素数的“强伪证”(strong liar)。
也就是说,当p是一个合数的时候,由于a是一定范围内随机选取的,对某次选取的a来说,上述两个式子不同时满足,这时称为p是基于a的大概率素数【注:1-1/4 = 3/4 (单次素数概率),上文提及】。
每个奇合数n都有很多个对应的凭证a,但并不容易直接找出这些a。当前解决的办法是使用概率性的测试。我们从集合中随机选择数a,然后检测当前的a是否是p为合数的一个凭证。
如果p本身确实是一个合数,那么大部分被选择的a都应该是n的凭证,也即通过这个测试能检测出n是合数的可能性很大[注:也有极小概率我们找到的a是一个“强伪证”(反而表明了n可能是一个素数]见举例说明]。
通过多次独立测试不同的a,我们能减少这种出错的概率,这就是Miller Rabin算法思想的核心。
对于测试一个大数是否是素数,通用的做法随机选取基数a,毕竟我们并不知道凭证和伪证在 [1, p-1]这个区间如何分布。
典型的例子是 Arnault 曾经给出了一个397位的合数n,但是所有小于307的基数a都是n是素数的“强伪证”。很不幸,如果函数通过检测a = 2,3,5,7,11这几种情况来进行素性检验,会被误判为素数。
所以使用Miller Rabin算法库,错误概率参数尽量设置非常低,即测试次数足够多。
实例说明
通过例子,更能清楚理解“强伪证”。
假设需要检验p = 221是否是一个素数。
首先$p - 1 = 220 =2^2 * 55$,于是我们得到了 k = 2和t = 55。我们随机从[1,p-1]中选取a,假设a = 174,于是有:
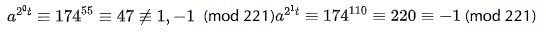
因为我们得到了一个-1,所以要么p = 221确实是一个素数,要么a = 174是一个“强伪证”。再尝试选取a=137,于是有:

可得,a = 137是 n = 221为合数的一个凭证,而a = 174是一个“强伪证”, 综合可得p = 221不是一个素数。
代码示例
具体实现代码容易在GitHub上找到,这里贴简单示例,方便直接查看(PC端阅读效果佳)
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <map>
using namespace std;
int number = 0;
map<long long, int>m;
long long Random( long long n )
//生成[ 0 , n ]的随机数
{
return ((double)rand( ) / RAND_MAX*n + 0.5);
}
long long q_mul( long long a, long long b, long long mod )
{//快速计算 (a*b) % mod
long long ans = 0;
while(b)
{
if(b & 1)
{
b--;
ans =(ans+ a)%mod;
}
b /= 2;
a = (a + a) % mod;
}
return ans;
}
long long q_pow( long long a, long long b, long long mod )
{ //快速幂模运算 (a^b) % mod
long long ans = 1;
while(b)
{
if(b & 1)
{
ans = q_mul( ans, a, mod );
}
b /= 2;
a = q_mul( a, a, mod );
}
return ans;
}
bool witness( long long a, long long n )//miller_rabin算法的核心
{ //用检验算子a来检验n是不是素数
long long tem = n - 1;
int j = 0;
while(tem % 2 == 0)
{
tem /= 2;
j++;
}
//将n-1拆分为a^r * s
long long x = q_pow( a, tem, n );
//得到a^r mod n
if(x == 1 || x == n - 1) return true;
//余数为1则为素数
while(j--) //否则试验条件2看是否有满足的 j
{
x = q_mul( x, x, n );
if(x == n - 1) return true;
}
return false;
}
bool miller_rabin( long long n, int times )
{ //检验n是否是素数
if(n == 2)
return true;
if(n < 2 || n % 2 == 0)
return false; //注:特别大的数使用BigInt
for(int i = 1; i <= times; i++) //做times次随机检验
{
long long a = Random( n - 2 ) + 1;
//得到随机检验算子 a
if(!witness( a, n ))
//用a检验n是否是素数
return false;
}
return true;
}可以看到用到了快速幂模运算等, 注意对于特别大的数使用BigInt,示例代码仅帮助理解。
小结
本节从"凭证"的角度来扩展说明了Miller Rabin算法,结合前文会有更好的理解。判断大素数的方法除了Miller Rabin这种概率性的算法,也有确定的算法,但是效率不高,未能广泛使用,故不再介绍。
有了数论,RSA,椭圆曲线密码学等基础,从下一篇起打算介绍VRF(随机可验证函数)的原理和在区块链中的应用。
欢迎关注公众号:blocksight
- 学分: 9
- 分类: 密码学基础
- 标签: Miller Rabin算法 区块链中的数学
- Uniswap v3 数学洞察系列翻译 —— 第六部分 共 6 部分 3836 浏览
- Uniswap v3 数学洞察系列翻译 —— 第五部分 共 6 部分 3944 浏览
- Uniswap v3 数学洞察系列翻译 —— 第四部分 共 6 部分 4381 浏览
- Uniswap v3 数学洞察系列翻译 —— 第三部分 共 6 部分 5238 浏览
- Uniswap v3 数学洞察系列翻译 —— 第二部分 共 6 部分 3344 浏览
- Uniswap v3 数学洞察系列翻译 —— 第一部分 共 6 部分 3922 浏览
- stark数学基础和翻译名词 3250 浏览
- 区块链中的数学--PLookup 7278 浏览
- 区块链中的数学 -- MultiSet check& Schwartz–Zippel lemma 6782 浏览
- 区块链中的数学 - 环签名(ring signature) 16080 浏览
- 区块链中的数学 -盲签名(Blind Signature) 13869 浏览
- 区块链中的数学 - sigma协议OR Proof&签名 7798 浏览

