Uniswap V3 流动性机制与限价订单解析：资金效率提升之道

Uniswap V3 引入了集中流动性和价格区间的创新机制，相较于 V2 显著提升了资金使用效率。本文通过数学推导、案例分析和限价订单实现，深入剖析 Uniswap V3 的流动性计算原理及其实际应用，适合对去中心化金融（DeFi）和自动化做市商（AMM）感兴趣的读者。

本文详细讲解了 Uniswap V3 中流动性的计算公式，推导了 X、Y Token 与流动性 L、价格 P 之间的关系，并通过案例分析展示了虚拟流动性如何将资金效率提升一倍。进一步探讨了限价订单的实现原理，揭示了价格区间设置对流动性和资金效率的影响。最后通过一个思考问题，引导读者深入理解流动性参数 L 的计算。

流动性计算

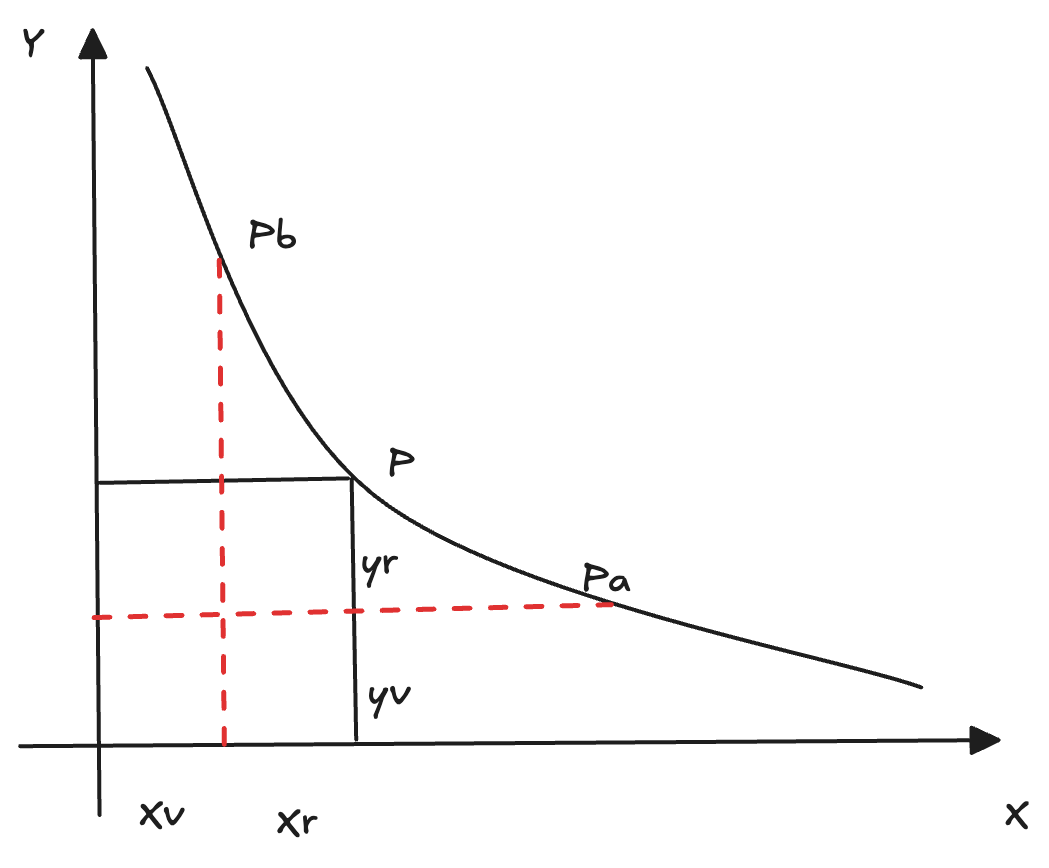
一、确定 x, y 与 L, P 的关系

推导 X

$$ \begin{align} x \cdot y = k = L^2 \ (Xr + Xv) \cdot (Yr + Yv) = k \ p = \frac{y}{x} \ x = \frac{L^2}{y} = \frac{L^2}{px} \ x^2 = \frac{L^2}{p} \ x = \frac{L}{\sqrt{{p}}} \end{align} $$

推导 Y

$$ \begin{align*} x \cdot y = k = L^2 \ p = \frac{y}{x} \ y = p \cdot x = p \cdot \frac{L^2}{y} \ y^2 = p \cdot L^2 \ y = L \cdot \sqrt{p}

\end{align*} $$

在 P = Pb 时

$$ \begin{align} x = Xv + Xr = \frac{L}{\sqrt{{Pb}}} \end{align} $$

因为 Xr = 0，故得出 $Xv = \frac{L}{\sqrt{{Pb}}}$

在 P = Pa 时

$$ \begin{align} y = Yr + Yv = L \cdot \sqrt{Pa} \end{align} $$

因为 Yr = 0，故得出 $Yv = L \cdot \sqrt{Pa}$

根据上述可推导公式如下： $$ \begin{align} x \cdot y = k = L^2 \ (Xr + Xv) \cdot (Yr + Yv) = k = L^2 \ (Xr + \frac{L}{\sqrt{{Pb}}}) \cdot (Yr + L \cdot \sqrt{Pa}) = k = L^2 \ (x + \frac{L}{\sqrt{{Pb}}}) \cdot (y + L \cdot \sqrt{Pa}) = L^2 \ \end{align} $$

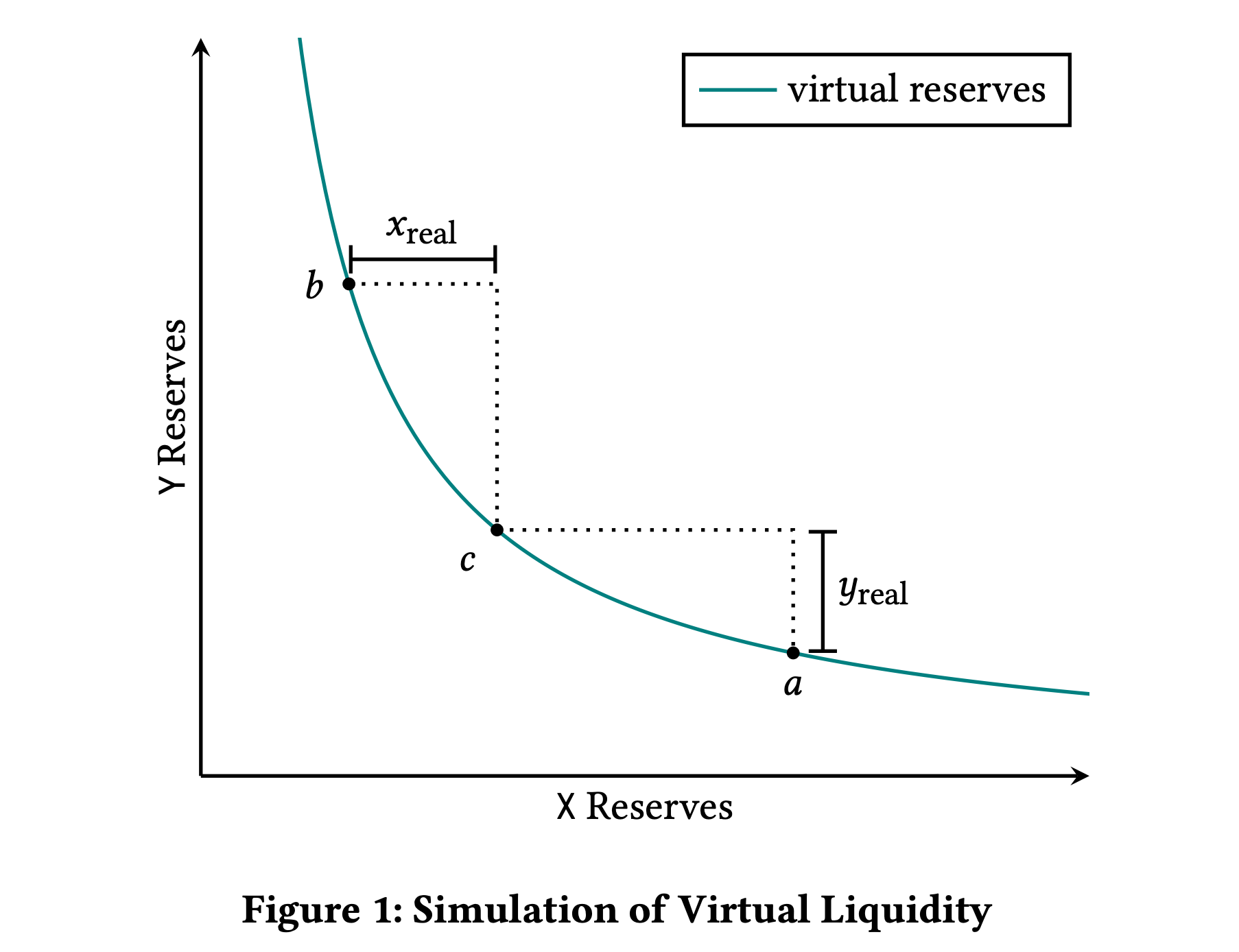
这就是 Uniswap V3 实际流动性和X、Y Token 数量关系的公式。这也是 Uniswap V3 白皮书中的公式 其实它本质上也是$ x \cdot y = k$ 的一个变种。

![image-20250522094943657.png](https://img.learnblockchain.cn/attachments/2025/05/XeKBQxqm682f...