Python、Solidity 和 EVM 中的双线性对

有时也称为双线性映射，双线性配对使我们能够取三个数字 $a$、$b$ 和 $c$，其中 $ab = c$，将它们加密为 $E(a)$、$E(b)$、$E(c)$，其中 $E$ 是加密函数，然后将两个加密值发送给验证者，验证者可以验证 $E(a)E(b) = E(c)$，但不知道原始值。我们可以使用双线性配对来证明第三个数字是前两个数字的乘积，而不需要知道前两个原始数字。

我们将在高层次上解释双线性配对，并提供一些 Python 示例。

先决条件

• 读者应该知道在椭圆曲线上下文中什么是 点加法 和标量乘法。
• 读者还应该了解在此上下文中的离散对数问题：一个标量乘以一个点会产生另一个点，并且在一般情况下计算给定椭圆曲线点的标量是不可行的。
• 读者应该知道什么是 有限域 和循环群，以及在椭圆曲线上下文中什么是生成元。我们将用变量 G 来引用生成元。
• 读者应该了解 Ethereum 预编译。我们将用大写字母表示 EC（椭圆曲线）点，用小写字母表示有限域的元素（“标量”）。当我们说元素时，它可以是有限域中的一个整数，也可以是椭圆曲线上的一个点。上下文将使其明确。

阅读本教程并不一定要完全理解以上所有内容，但对这个主题建立良好的直觉会更加困难。

双线性配对如何工作

当一个标量乘以椭圆曲线上的一个点时，会产生另一个椭圆曲线点。即 $P = pG$ 其中 $p$ 是标量，而 $G$ 是生成元。给定 $P$ 和 $G$ 我们无法确定 $p$。

假设 $pq = r$。我们想要做的是取

$$ \begin{align} P = pG\\ Q = qG\\ R = rG\\ \end{align} $$

并让验证者相信 $P$ 和 $Q$ 的离散对数相乘得出 $R$ 的离散对数。

如果 $pq = r$，并且 $P = pG$、$Q = qG$、$R = rG$，那么我们希望有一个函数满足

$$f(P,Q)=R$$

当 $pq ≠ r$ 时不等于 $R$。这应对所有可能的 $p$、$q$ 和 $r$ 的组合都成立。

然而，通常我们在使用双线性配对时并不是这样表示 $R$。出于我们稍后会讨论的原因，它通常计算为

$$f(P,Q) = f(R,G)$$

$G$ 是生成点，可以被看作“五线谱”中的 $1$。在这个上下文中。例如，$pG$ 表示我们进行了 $(G + G + … + G)$ $p$ 次。$G$ 仅意味着我们取了 $G$ 并没有添加任何内容。所以在某种意义上，这与说 $P \times Q = R \times 1$ 是相同的。

所以我们的双线性配对是一个函数，如果你插入两个椭圆曲线点，你将得到一个与这两个点的离散对数乘积相对应的输出。

符号

双线性配对通常写作 $e(P, Q)$。这里，$e$ 与自然对数无关，$P$ 和 $Q$ 是椭圆曲线点。

一般化，检查两个乘积是否相等

假设某人给了我们四个椭圆曲线点 $P_1$、$P_2$、$Q_1$ 和 $Q_2$，并声称 $P_1$ 和 $P_2$ 的离散对数的乘积与 $Q_1$ 和 $Q_2$ 的离散对数的乘积相同，即 $p_1p_2 = q_1q_2$。使用双线性配对，我们可以在不知道 $p_1$、$p_2$、$q_1$ 或 $q_2$ 的情况下检查这是否正确。我们只需执行：

$$e(P_1, P_2) \stackrel{?}{=} e(Q_1, Q_2)$$

“双线性”意味着什么

双线性意味着如果一个函数取两个参数，而其中一个保持不变，而另一个变化，那么输出会线性地随着非稳态参数变化。

如果 $f(x,y)$ 是双线性的，并且 $c$ 是常量，则 $z = f(x, c)$ 随着 $x$ 线性变化，而 $z = f(c, y)$ 随着 $y$ 线性变化。

我们可以从中推断出椭圆曲线双线性配对具有以下属性：

$$ f(aG, bG) = f(abG, G) = f(G, abG) $$

$e(P, Q)$ 返回什么？

老实说，输出的数学复杂程度较高，试图真正解释它是反生产的。这就是为什么本书早期的大部分时间专注于解释群体，因为理解群体是什么比理解 $e(P, Q)$ 返回什么要容易得多。

双线性配对的输出是群元素，具体来说是有限循环群的元素。

最好将 $e(P, Q)$ 视为一个黑盒，类似于大多数程序员将哈希函数视为黑盒。

然而，尽管它是一个黑盒，我们仍然知道输出的很多属性，我们称之为 $G_T$：

• $G_T$ 是一个循环群，因此它具有封闭的二元运算符。
• $G_T$ 的二元运算符是协会的。
• $G_T$ 有一个单位元。
• $G_T$ 中的每个元素都有一个逆。
• 因为这个群是循环的，所以它有一个生成元。
• 因为这个群是循环的和有限的，所以有限循环群同态映射到 $G_T$。即，我们有某种方法将有限域中的元素同态映射到 $G_T$ 中的元素。

因为这个群是循环的，我们对 $G_T$、$2G_T$、$3G_T$ 等都有一个概念。$G_T$ 的二元运算符大致称作“乘法”，所以 $8G_T = 2G_T * 4G_T$。

如果你真的想知道 $G_T$ “看起来像什么”，它是一个 12 维对象。然而，单位元并没有那么可怕：

$$(1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)$$

对称群和非对称群

上述符号意味着，我们在说

$$e(aG, bG) = e(abG, G)$$

时在各处使用相同的生成元和椭圆曲线群。然而，实际上，事实证明在两个参数的不同群（但同一阶）中创建双线性配对会更加容易。

具体来说，我们说：

$$e(a, b) → c, \space\space a ∈ G_1, b ∈ G_2, c ∈ G_T$$

所用的群是不同的。

然而，我们关心的属性依然成立。

$$e(aG_1, bG_2) = e(abG_1, G_2) = e(G_1, abG_2)$$

在上述方程中，群 $G_T$ 并未明确显示，但这是 $e(G_1, G_2)$ 的值域（输出空间）。

可以将 $G_1$ 和 $G_2$ 看作是具有不同参数（但相同数量点）的不同椭圆曲线方程，这样的说法是正确的，因为它们是不同的群。

在对称配对中，双线性配对函数的两个参数使用相同的椭圆曲线群。这意味着用于两个参数的生成元和椭圆曲线群是相同的。在这种情况下，配对函数通常表示为：

$$e(aG_1, bG_1) = e(abG_1, G_1) = e(G_1, abG_1)$$

在非对称配对中，参数使用不同的群。例如，第一个参数可以使用与第二个参数不同的生成元和椭圆曲线群。配对函数仍然可以满足所需的属性：

$$e(aG_1, bG_2) = e(abG_1, G_2) = e(G_1, abG_2)$$

在实践中，我们使用非对称群，所使用的组之间的差异将在下一节中解释。

$G_1$ 是我们在前几章中讨论的同一组，在以太坊的上下文中，它是我们从库中导入的相同 G1：

from py_ecc.bn128 import G1

我们还可以从同一库中导入 G2，如下所示：

from py_ecc.bn128 import G1, G2

但什么是 $G_2$？

字段扩展和 Python 中的 G2 点

双线性配对对你选择的群类型相当陌生，但 Ethereum 的 $G_2$ 使用带有字段扩展的椭圆曲线。如果你希望能阅读使用 ZK-SNARK 的 Solidity 代码，你至少需要对这些东西有一个大致的了解。

我们通常将 EC 点视为两个点 $x$ 和 $y$。通过 字段扩展，$x$ 和 $y$ 本身变成二维对象 $(x, y)$ 对。这类似于复数如何“扩展”实数并将它们变成具有 2 维的东西（一个实成分和一个虚成分）。

字段扩展是一个非常抽象的概念，坦率地说，字段及其扩展之间的关系从纯函数概念来看并不重要。

你只需这样想：

$G_2$ 中的椭圆曲线是一个椭圆曲线，其中 $x$ 和 $y$ 元素都是二维对象。

Python 中的 G2 点

理论讲得够多了，让我们编码看看一个 $G_2$ 点。按如下方式安装 py_ecc 库。

python -m pip install py_ecc

现在让我们从中导入我们需要的函数：

from py_ecc.bn128 import G1, G2, pairing, add, multiply, eq

print(G1)
## (1, 2)
print(G2)
##((10857046999023057135944570762232829481370756359578518086990519993285655852781, 11559732032986387107991004021392285783925812861821192530917403151452391805634), (8495653923123431417604973247489272438418190587263600148770280649306958101930, 4082367875863433681332203403145435568316851327593401208105741076214120093531))

如果你仔细看看，你会看到 G2，G2 是一个元组对。第一个元组是二维 $x$ 点，第二个元组是二维 $y$ 点。

G1 和 G2 是各自群的生成点。

G1 和 G2 的阶数（曲线上的点数量）是相同的：

from py_ecc.bn128 import G1, G2, eq, curve_order, multiply, eq, curve_order

x = 10 # 随机选择
assert eq(multiply(G2, x + curve_order), multiply(G2, x))
assert eq(multiply(G1, x + curve_order), multiply(G1, x))

虽然 G2 点可能看起来有点奇怪，但它们的行为与我们熟悉的其他循环群相同。这意味着我们可以按照预期通过标量乘法（即重复 addition）构造其他点。

print(eq(add(G1, G1), multiply(G1, 2)))
## True
print(eq(add(G2, G2), multiply(G2, 2)))
## True

显然，你只能加相同群的元素。

add(G1, G2) # TypeError

顺便说一句，这个库重载了一些算术运算符（你可以这样做），这意味着你可以这样做：

print(G1 + G1 + G1 == G1*3)
## True

## 上述与此相同：
eq(add(add(G1, G1), G1), multiply(G1, 3))
## True

Python 中的双线性配对

在本文开头，我们提到双线性配对可以检查 $P$ 和 $Q$ 的离散对数是否乘积等于 $R$，即 $PQ = R$。

以下是如何在 Python 中实现的：

from py_ecc.bn128 import G1, G2, pairing, multiply, eq

P = multiply(G1, 3)
Q = multiply(G2, 8)

R = multiply(G1, 24)

assert eq(pairing(Q, P), pairing(G2, R))

相当烦人的是，库要求你将 G2 点作为 pairing 的第一个参数传递。

产品的相等性

在本文开头，我们提到一个配对可以检查：

$$e(P_2, P_1) \stackrel{?}{=} e(Q_2, Q_1)$$

以下是如何在 Python 中实现的：

from py_ecc.bn128 import G1, G2, pairing, multiply, eq

P_1 = multiply(G1, 3)
P_2 = multiply(G2, 8)

Q_1 = multiply(G1, 6)
Q_2 = multiply(G2, 4)

assert eq(pairing(P_2, P_1), pairing(Q_2, Q_1))

$G_T$ 的二元运算符

$G_T$ 中的元素通过“乘法”组合，但请记住，这实际上是 Python 中的一个语法重载：

from py_ecc.bn128 import G1, G2, pairing, multiply, eq

## 2 * 3 = 6
P_1 = multiply(G1, 2)
P_2 = multiply(G2, 3)

## 4 * 5 = 20
Q_1 = multiply(G1, 4)
Q_2 = multiply(G2, 5)

## 10 * 12 = 120 (6 * 20 = 120 也可以)
R_1 = multiply(G1, 10)
R_2 = multiply(G2, 12)

assert eq(pairing(P_2, P_1) * pairing(Q_2, Q_1), pairing(R_2, R_1))

## 失败！

但断言失败了！

$G_T$ 中的元素表现得像“基础”的“幂”。

回顾代数：

$$b^xb^y = b^{x+y}$$

假设我们生成一个在 $G_T$ 中的元素为 $e(3G_2, 2G_1)$。我们可能认为元素是 $6G_T$，但更有帮助地想象它是 $b^6G_T$。在这个上下文中，没有必要知道 $b$ 是什么，仅仅知道它存在。

因此，为了使我们上面的代码正常工作，需要将 $R_1$ 和 $R_2$ 修改为乘积为 26。

我们的代码实际上计算的是：

$$ \begin{align} b ^ {2 \cdot 3} b ^ {4 \cdot 5} = b ^ {13 \cdot 2}\\ b ^ 6 \cdot b ^ {20} = b ^ 26 \end{align*} $$

from py_ecc.bn128 import G1, G2, pairing, multiply, eq

## 2 * 3 = 6
P_1 = multiply(G1, 2)
P_2 = multiply(G2, 3)

## 4 * 5 = 20
Q_1 = multiply(G1, 4)
Q_2 = multiply(G2, 5)

## 13 * 2 = 26
R_1 = multiply(G1, 13)
R_2 = multiply(G2, 2)

## b ^ {2 * 3} * b ^ {4 * 5} = b ^ {13 * 2}
## b ^ 6 * b ^ 20 = b ^ 26

assert eq(pairing(P_2, P_1) * pairing(Q_2, Q_1), pairing(R_2, R_1))

Ethereum 中的双线性配对

EIP 197 规范

py_ecc 库实际上由 以太坊基金会 维护，它也支持 PyEVM 实现中地址为0x8的预编译。

以太坊在 EIP-197 中定义的预编译在 G1 和 G2 中操作点，并 隐式 在 $G_T$ 中操作点。

该预编译的规范最开始看起来可能有些奇怪。它接受一个格式如下的 G1 和 G2 点列表：

A₁B₁A₂B₂...AₙBₙ : Aᵢ ∈ G1, Bᵢ ∈ G2

这些是最初创建的

A₁ = a₁G1
B₁ = b₁G2
A₂ = a₂G1
B₂ = b₂G2
...
Aₙ = aₙG1
Bₙ = bₙG2

如果以下条件为真，则预编译返回 1

a₁b₁ + a₂b₂ + ... + aₙbₙ = 0

否则则返回零。

这乍一看可能会让人有点摸不着头脑！这似乎暗示预编译正在计算每个点的离散对数，通常被认为是不可行的。此外，它为什么不行为与早期 Python 示例中的配对？早期示例返回 $G_T$ 中的一个元素，但此预编译返回布尔值。

EIP 197 设计决策的理由

第一个问题是 $G_T$ 中的元素是大的，特别是，它们是 12 维对象。

这将占用大量内存，导致更高的 gas 成本。此外，由于大多数 ZK 验证算法的工作原理（这超出了本文的范围），我们通常不会检查配对的输出值，而只检查它是否与其他配对相等。特别是在 Groth16（由 Tornado Cash 使用的零知识算法）的最终步骤如下：

$$ e(A₁, B₂) = e(α₁, β₂) + e(L₁, γ₂) + e(C₁, δ₂) $$

其中，每个变量为基于它的下标符号（我们本可以使用大写希腊字母保持一致性，但这些字母与拉丁字母过于相似）。

这些变量的含义在此阶段并不重要。重要的是，它可以作为“产品”的和（椭圆曲线配对）来写。具体来说，我们可以将其写为

$$ 0 = e(−A₁, B₂) + e(α₁, β₂) + e(L₁, γ₂) + e(C₁, δ₂) $$

而现在它完美匹配预编译规范！

不仅仅是 Groth16，许多 zk 算法的验证公式都看起来像这样，这就是预编译设计为与配对的和一起工作而不是返回单一配对值的原因。

如果我们查看 Tornado Cash 的验证代码，我们可以看到它正在准确地实现这一点（甚至希腊字母也匹配，但如果你还未理解这点无需担心）。$\beta_2$ 仅表示它是一个 $\mathbb{G}_2$ 点，$\alpha_1$ 表示 $\mathbb{G}_1$ 点，等等。

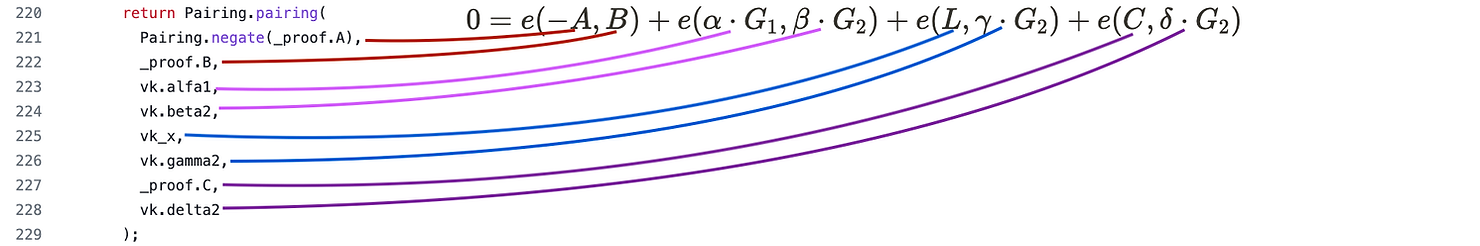
在配对函数中，调用 address(8) 完成配对计算并确定证明是否有效。

_有时，群 $GT$ 在 EIP 197 的上下文中被称为 $G{12}$。_

离散对数的和

这里的关键见解是，如果

$$ab + cd = 0$$

那么它也必须是真的：

$$A₁B₂ + C₁D₂ = 0₁₂ \space\space\space\space A₁,C₁ ∈ G1, B₂,D₂ ∈ G2$$

在 $\mathbb{G}_{12}$ 群中。

预编译实际上并不计算离散对数，它只是检查配对的和是否为零。

配对的和等于零如果且仅当离散对数的乘积的和为零。

双线性配对的端到端 Solidity 示例

让我们拿这些输入 a、b、c 和 d。

a = 4
b = 3
c = 6
d = 2

-ab + cd = 0

将其放入公式中，我们可以得到

$$ A₁B₂ + C₁D₂ = e(−aG1, bG2) + e(cG1, dG2) = 0 $$

在 Python 中这将等同于

from py_ecc.bn128 import neg, multiply, G1, G2
a = 4
b = 3
c = 6
d = 2
## 取 G1 * a 的负数以使方程求和为 0

print(neg(multiply(G1, a)))
##(3010198690406615200373504922352659861758983907867017329644089018310584441462, 17861058253836152797273815394432013122766662423622084931972383889279925210507)
print(multiply(G2, b))
## ((2725019753478801796453339367788033689375851816420509565303521482350756874229, 7273165102799931111715871471550377909735733521218303035754523677688038059653), (2512659008974376214222774206987427162027254181373325676825515531566330959255, 957874124722006818841961785324909313781880061366718538693995380805373202866))
print(multiply(G1, c))
## (4503322228978077916651710446042370109107355802721800704639343137502100212473, 6132642251294427119375180147349983541569387941788025780665104001559216576968)
print(multiply(G2, d))
## ((18029695676650738226693292988307914797657423701064905010927197838374790804409, 14583779054894525174450323658765874724019480979794335525732096752006891875705), (2140229616977736810657479771656733941598412651537078903776637920509952744750, 11474861747383700316476719153975578001603231366361248090558603872215261634898))

以下是具有结构化格式的输出

aG1_x = 3010198690406615200373504922352659861758983907867017329644089018310584441462,
aG1_y = 17861058253836152797273815394432013122766662423622084931972383889279925210507,

bG2_x1 = 2725019753478801796453339367788033689375851816420509565303521482350756874229,
bG2_x2 = 7273165102799931111715871471550377909735733521218303035754523677688038059653,
bG2_y1 = 2512659008974376214222774206987427162027254181373325676825515531566330959255,
bG2_y2 = 957874124722006818841961785324909313781880061366718538693995380805373202866,

cG1_x = 4503322228978077916651710446042370109107355802721800704639343137502100212473,
cG1_y = 6132642251294427119375180147349983541569387941788025780665104001559216576968,

dG2_x1 = 18029695676650738226693292988307914797657423701064905010927197838374790804409,
dG2_x2 = 14583779054894525174450323658765874724019480979794335525732096752006891875705,
dG2_y1 = 2140229616977736810657479771656733941598412651537078903776637920509952744750,
dG2_y2 = 11474861747383700316476719153975578001603231366361248090558603872215261634898

现在我们将值加密为 $\mathbb{G}_1$ 和 $\mathbb{G}_2$ 群中的点，其他人或程序可以确认我们计算 $e(A_1,B_2)+e(C_1,D_2)=0$ 正确无误，而无需知道 a、b、c 或 d 的具体值。以下是一个 Solidity 合约，利用 ecPairing 预编译来确认我们是否计算出有效的值。

我们创建一个 Pairings.sol 文件以 在 Foundry 中进行单元测试（我们将在下文提供测试文件）

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.13;
contract Pairings {
    /** 
     *  返回 true 如果 == 0,
     *  返回 false 如果 != 0,
     *  如果无效配对则还原并出现 "Wrong pairing"
     */
     function run(uint256[12] memory input) public view returns (bool) {
        assembly {
            let success := staticcall(gas(), 0x08, input, 0x0180, input, 0x20)
            if success {
                return(input, 0x20)
            }
        }
        revert("Wrong pairing");
    }
}

我们使用此 Foundry 测试文件来部署并调用我们的 Pairings 合约，以确认我们的 ecPairing 计算。以下文件我们称为 TestPairings.sol。

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.13;
import "forge-std/Test.sol";
import "../src/Pairings.sol";

contract PairingsTest is Test {
    Pairings public pairings;

    function setUp() public {
        pairings = new Pairings();
    }

    function testPairings() public view {
        uint256 aG1_x = 3010198690406615200373504922352659861758983907867017329644089018310584441462;
        uint256 aG1_y = 17861058253836152797273815394432013122766662423622084931972383889279925210507;

        uint256 bG2_x1 = 2725019753478801796453339367788033689375851816420509565303521482350756874229;
        uint256 bG2_x2 = 7273165102799931111715871471550377909735733521218303035754523677688038059653;
        uint256 bG2_y1 = 2512659008974376214222774206987427162027254181373325676825515531566330959255;
        uint256 bG2_y2 = 957874124722006818841961785324909313781880061366718538693995380805373202866;

        uint256 cG1_x = 4503322228978077916651710446042370109107355802721800704639343137502100212473;
        uint256 cG1_y = 6132642251294427119375180147349983541569387941788025780665104001559216576968;

        uint256 dG2_x1 = 18029695676650738226693292988307914797657423701064905010927197838374790804409;
        uint256 dG2_x2 = 14583779054894525174450323658765874724019480979794335525732096752006891875705;
        uint256 dG2_y1 = 2140229616977736810657479771656733941598412651537078903776637920509952744750;
        uint256 dG2_y2 = 11474861747383700316476719153975578001603231366361248090558603872215261634898;

        uint256[12] memory points = [
            aG1_x,
            aG1_y,
            bG2_x2,
            bG2_x1,
            bG2_y2,
            bG2_y1,
            cG1_x,
            cG1_y,
            dG2_x2,
            dG2_x1,
            dG2_y2,
            dG2_y1
        ];

        bool x = pairings.run(points);
        console2.log("result:", x);
    }
}

请注意，G2 点的排列方式与 Python 中 G2 点的排列方式不同。

这通过并打印出 true 到控制台。请注意，点已经按其变量名、所属群体以及如果它们表示椭圆曲线点的 x 或 y 进行了标记。

值得注意的是，ecPairing 预编译不期望或要求数组，而我们选择以行内汇编的方式使用数组只是可选的。你可以通过 Solidity 直接做同样的事情，代码如下：

function run(bytes calldata input) public view returns (bool) {
    // 可选，预编译也会检查这一点，如果不正确则还原（没有错误），这有助于缩小可能的错误
    if (input.length % 192 != 0) revert("Points must be a multiple of 6");
    (bool success, bytes memory data) = address(0x08).staticcall(input);
    if (success) return abi.decode(data, (bool));
    revert("Wrong pairing");
}

并将测试文件更新为：

function testPairings() public view {
    uint256 aG1_x = 3010198690406615200373504922352659861758983907867017329644089018310584441462;
    uint256 aG1_y = 17861058253836152797273815394432013122766662423622084931972383889279925210507;

    uint256 bG2_x1 = 2725019753478801796453339367788033689375851816420509565303521482350756874229;
    uint256 bG2_x2 = 7273165102799931111715871471550377909735733521218303035754523677688038059653;
    uint256 bG2_y1 = 2512659008974376214222774206987427162027254181373325676825515531566330959255;
    uint256 bG2_y2 = 957874124722006818841961785324909313781880061366718538693995380805373202866;

    uint256 cG1_x = 4503322228978077916651710446042370109107355802721800704639343137502100212473;
    uint256 cG1_y = 6132642251294427119375180147349983541569387941788025780665104001559216576968;

    uint256 dG2_x1 = 18029695676650738226693292988307914797657423701064905010927197838374790804409;
    uint256 dG2_x2 = 14583779054894525174450323658765874724019480979794335525732096752006891875705;
    uint256 dG2_y1 = 2140229616977736810657479771656733941598412651537078903776637920509952744750;
    uint256 dG2_y2 = 11474861747383700316476719153975578001603231366361248090558603872215261634898;

    bytes memory points = abi.encode(
        aG1_x,
        aG1_y,
        bG2_x2,
        bG2_x1,
        bG2_y2,
        bG2_y1,
        cG1_x,
        cG1_y,
        dG2_x2,
        dG2_x1,
        dG2_y2,
        dG2_y1
    );

    bool x = pairings.run(points);
    console2.log("result:", x);
}

这同样通过并返回 true，正如最初的实现，因为它向预编译发送了完全相同的 calldata。

区别在于，在第一个实现中，测试文件将一个指向预编译的点数组发送到配对合约，而使用行内汇编将前 32 字节（数组长度）切掉，将其余部分发送到预编译。而在第二个实现中，测试文件将abi编码的点发送到配对合约并原样转发到预编译。

从 RareSkills 了解更多

这些材料取自我们的 零知识课程。请查看该课程以获得更多信息。

我真的想理解双线性配对背后的数学

你已经被警告，数学非常复杂，理解它并不会帮助你实际实现 ZK 证明，这是本书的目标。你可能在不知道它们的内部工作的情况下有效地使用 SHA-256 或 Keccak256，我们 强烈 建议你在此阶段将配对视为同样的东西。尽管如此，如果你没有被我们的警告劝阻，这里有一个很好的资源，如果你仍然想深入了解： 初学者的配对。 这里会有龙。

最初发布于 2023 年 7 月 18 日

• 原文链接： rareskills.io/post/bilin...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～