区块链时代的拜占庭将军们（上）

区块链时代的拜占庭将军们（上） 区块链时代的拜占庭将军们（中） 区块链时代的拜占庭将军们（下）

It is not sufficient that everyone knows X. We also need everyone to know that everyone knows X, and that everyone knows that everyone knows that everyone knows X - which, as in the Byzantine Generals problem, is the classic hard problem of distributed data processing. （译文：所有人都知道X是不够的。我们还需要所有人都知道所有人都知道X，以及所有人都知道所有人都知道所有人都知道X，就像是在拜占庭将军问题里的那样——这是个分布式数据处理中的经典的困难问题。） ——James A. Donald

以上，是James Donald，有迹可查的第一位在中本聪发布比特币白皮书之后与中本聪互动的人向他提出的问题，也是拜占庭将军这个经典问题与区块链的第一次碰撞。

中本聪举了个例子来回答这个问题：

这个例子实际上从侧面反映了中本聪这个人——1，他是个民科，但是和被我们嘲讽的民科不同，他会和真正的科学家讨论，而且，他深入地研究了前人的成果。可以说，中本聪才应该是所有民科的学习对象，他在不被官方承认的情况下，通过学习，思考，意志和行动力，单枪匹马用一个社会实验，而不是学术论文，开创了一个明星领域；2，但是他确实是个民科，无论是白皮书还是这个回答，他都没能讲清楚比特币与前人成果的区别和联系，而这是正经的学术研究中必须要考虑的问题，因为正儿八经的学术论文里如果你不把背景写清楚显然是通不过同行评议的。当然，中本聪没有这个顾虑，他直接发表了比特币白皮书，然后发表了比特币。他的回答既不好懂也不怎么准确，从后面的反应中我们也看到，James同学也并没有完全信服。实际上，真正准确的描述了为什么比特币和拜占庭容错的关系的论文，要等到2015年，即中本聪创造了比特币白皮书的7年之后的《The Bitcoin Backbone Protocol》。

拜占庭将军问题以及拜占庭将军问题以及比特币之间的关系，我之前的关于比特币的文章中已经有所提及，而大家也可能在其他的科普文章中看过（大概有一半的可能性你看到的是关于两军问题的描述）。但是拜占庭将军问题和区块链的渊源和纠葛却远远不止于此。我在这篇文章里会试图从一个比较特别的视角去重新审视拜占庭将军和区块链之间的关系。更确切地说，我会用三篇的篇幅，写以下内容：

1. 关于异步拜占庭容错问题的介绍。
2. 从区块链的视角，回顾BFT算法的发展。这是一个全新的视角，因为通过区块链了解到这个问题的人，大概率是看不懂BFT算法的论文的，即便看懂了，也很难理清它和区块链以及Nakamoto类共识算法的关系，因为两者的用词和描述场景都有很大的区别。
3. 介绍BFT算法在区块链领域中的发展，以及对于BFT算法应该如何用于区块链共识算法的一些展望。

这里写的，大概率是你在别的地方看不到的，无论是科普文章，还是专业文献，无论是中文，还是英文。

拜占庭将军的由来

这是个大部分计算机系科班出身的人和区块链爱好者都熟悉的故事了——拜占庭将军问题，即，三个将军，如何在其中一个是叛徒的情况下，通过互相之间派信使传令的方式，让两个诚实的将军达成一致。

这个问题在1982年由图灵奖得主，分布式系统的奠基人之一Leslie Lamport于1982年和他的两个同事一起提出：

The Byzantine Generals Problem

更准确地说，这个问题应该这么表述：

三个拜占庭将军，其中一个是指挥官。三个人其中一个人是叛徒，他的目的就是造成诚实将军之间的不一致。

这时，我们希望：

1. 如果指挥官是诚实的，那么诚实的将军必须听从指挥官的命令。
2. 如果指挥官是叛徒，那么两个诚实的将军必须做出一致的决定。

也许很多人都已经知道，这个问题是无解的，原因如下：

1. 将军收到“进攻”的指令的时候，他不能直接做出“进攻”的判定，因为指挥官可能是叛徒。
2. 于是将军收到指令之后，它必须向另一名将军询问指挥官给另一名将军的指令。
3. 假设这个时候将军从指挥官那收到了“进攻”，而另一名将军却告诉他“指挥官跟我说的是撤退”。而这个时候，这位将军就会陷入一个困境：第一种可能是，指挥官是诚实的并且向两个将军都下达了“进攻”的指令，但是另一名将军是叛徒并且篡改了指挥官的命令；而另一种可能是，指挥官是叛徒并且向两个将军各下达了不同的指令。作为这位可怜的将军，他无法分别这两种情况。
4. 这里来到了问题的重点：我们并不关心他的决定究竟是“进攻”还是“撤退”，我们关心的是，如果我们预设任何一种战术，例如：遇到上述情况时选择“进攻”（“撤退”），它能在某一种可能的时候达成目标，但是在另一种可能的时候失效。

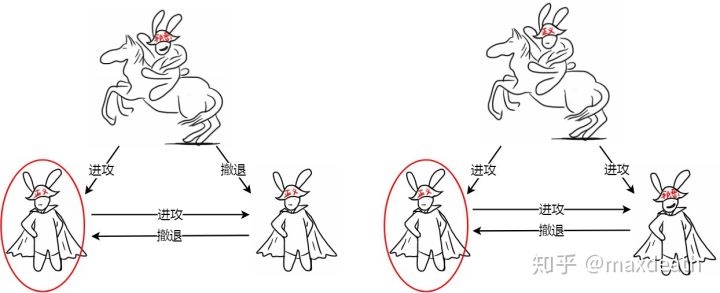同步拜占庭，左下的将军无法分辨两种情况

换句话说，当我们在说这个问题无解的时候，我们真正的意思是：

“任何一个确定性的算法都没法保证诚实节点能在任何情况下达成共识。”

然后，对于拜占庭将军问题，我们还知道另一个著名的答案：

这个问题在有四个将军的情况下有解。推而广之，不少于3f+1个将军的情况下，我们可以容下f个叛徒的存在。确切地说，我们能够找到一种算法，使得无论那f个叛徒怎么捣乱，剩下的不少于2f+1个的节点总是能够达成共识。

大部分关于拜占庭将军问题的科普到此为止……

——————————————————————————————————

然而，如果看到这里你就认为已经理解了拜占庭容错，从而也就理解了比特币试图解决的问题，你就大错特错了——拜占庭容错这个问题困难的部分还没开始呢。

这个时候，我们就不得不说拜占庭将军问题的提出者Leslie Lamport和他提出这个问题的背景了——

很多人知道Leslie Lamport是图灵奖获得者，也有很多人知道他可以说是分布式算法的奠基人之一，但是并不是很多人知道，当他提出拜占庭将军问题的时候，他正在SRI，为NASA做关于航天飞机航电系统的研究。同样，也没什么人知道，他不仅仅是分布式系统的奠基人，也是数字签名的先驱。换句话说，拜占庭容错的想法，完完全全脱胎于一般容错的航电系统。而Lamport在写下拜占庭将军问题这篇论文的时候，他并没有考虑到异步拜占庭将军的问题。而他之所以会提出这个问题，其实是想要说明刚刚诞生不久的RSA和数字签名的作用，例如，他刚刚提出不久的这篇关于数字签名的论文。

对于拜占庭将军问题，他提出的解决方案就是加入签名，而且，他在论文中提出了加入签名之后解决拜占庭将军问题的算法。结论就是，加入了签名之后，即便全世界只有两个将军是诚实的而其他将军全是叛徒，这两个将军也能达成共识。

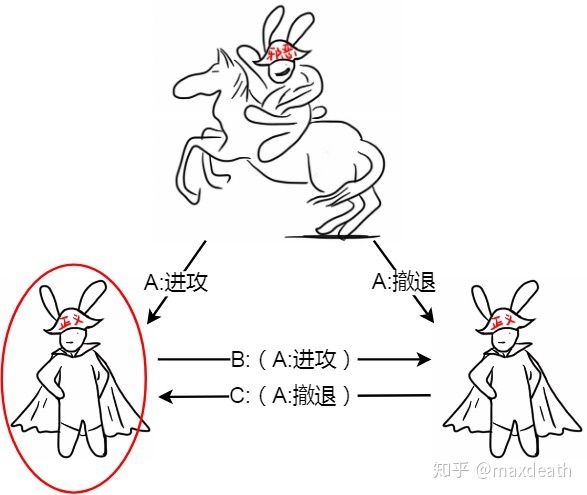将军B此时能够知道指挥官A是叛徒

异步拜占庭容错

然后，拜占庭容错，异步系统和数字签名无疑给分布式系统的研究者们打开了一闪新世界的大门，没过多久，异步系统（网络）的拜占庭容错问题就摆在了研究者的面前。而后面，无论是James Donald提到的拜占庭容错，还是中本聪通过POW解决的拜占庭容错问题，乃至由于区块链变得火起来的拜占庭容错这个问题，其实指的都是异步拜占庭容错。

在介绍异步拜占庭容错之前，我们要先说说什么是异步网络。

异步网络，顾名思义，和同步网络相反。两者的区别在于，在异步网络中，你发送的任何消息到达的延迟是不定的。更具体一点的话，我们说：

在同步网络中，存在某个延迟t，任何两点之间的通信消息延迟都小于t。

在异步网络中，不存在这么个t。

那么，在异步网络里，拜占庭节点实际上就获得了更大的能力——它可以做任何事来试图造成系统的不一致，那么自然，它可以假装失效节点，即不响应。也可以选择性地对一些人响应，一些人不响应。而且，他还可以任意控制自己响应的时间。

这个可能看上去并不好懂，那么我们举个例子来说明异步系统里的容错问题有多难：

小明想知道暗恋的女生小红是不是喜欢他，于是他发了条信息给小红：“你喜欢我吗？”如果小红回答：“嗯。”，小明得到正面的答案。如果小红回答“滚”，那么小明就得到负面的答案。

在同步系统里，我们可以在算法中约定小明在问完之后等待小红的答复，因为小红的答复一定会在时间t之前到达。

而在异步系统里，如果小红没有恶意，那么她会答复，但是她有可能很羞涩地选择了寄封信过来而不是直接发微信。于是，这条答复有可能会由于快递的原因，延迟任意长的时间。

当然，如果痴情的小明愿意等，我们还是可以说一句，他最终还是能等到小红的回信的。

但这是不考虑小红有恶意的情况。

而假设小红并不喜欢小明，而且压根不想理会他。

这个时候就会出现一个问题——痴情的小明同学可能会一根筋地相信，一定是信件的邮寄途中出了什么问题，小红怎么可能不给我回信。于是，他就算等白了头发，也可能永远不知道一个残酷的事实——

小红收到信看了一眼就丢掉了。

对于一切算法，我们都有一个基本的要求，叫终止，或者叫活性或者可用性。换句话说，我们需要一个能够获知小红喜不喜欢他的算法，我们可以接受得到结果的时间不定，但是我们不能接受最终能不能够得到结果随缘——也就是说，小明在发信之前来到山上找一个老禅师：

“有没有知道小红心意的办法？”

老禅师听了只是一言不发，笑而不语。

过了很久，小明终于恍然大悟：

“所以大师是说我只要一直等总能知道她的心意的对不对？”

于是欢天喜地地离开了。

“等等！我只是想用实际行动说明这个问题无解……”

实际上，两个人的异步系统中，在消息有可能丢失的条件下，这个叫“两军问题”，这个问题无解，这揭示了异步系统中的容错问题，或者说异步系统中的共识问题有多难。

但请注意，这里的两军问题可以说是拜占庭容错问题的两人版本，也可以说是一般容错问题的两人版本——因为两个人里，不存在误导他人的可能。而拜占庭错误和一般错误的最大的不同，就是拜占庭节点允许向不同的人发送不一致的消息。

那我们回到异步拜占庭将军问题，其实和之前拜占庭将军的条件一样，只不过多了一个终止的假设。

1. 如果将军是诚实的，那么诚实的士兵必须听从将军的命令。
2. 如果将军是叛徒，那么两个诚实的士兵必须做出一致的决定。
3. 这个算法必须最终使得大家做出决定。

这个问题，在三将军的情况下再次变得没有解了，即便加上了签名也一样。

说假话与不说话

三将军问题在异步系统里无解的我们可以认为是这个问题多了一个维度。但也可以理解成，加上了异步假设之后，拜占庭节点的能力变强了——之前，它只能通过谎报军情来迷惑其他人造成不一致，而现在，他多了一个选项，他可以假装断线不说话。

那么，说假话和不说话这两招，到底哪招更厉害呢？生活常识可能告诉我们说假话可能更难对付一些，但是实际上，生活中说假话难对付最大的原因就是因为没有签名，因此，当签名被引入之后，说假话的威胁其实已经被降到了最低——签名主要有两个作用：1，别人没法伪造你说的话；2，你说过的话自己也不能否认。于是，一个诚实的将军，叛徒无法伪造他说过的话，而一个叛徒指挥官如果有心误导，那么他所发的不一致的消息如果被诚实的将军收到，那么立刻就能判断出他是叛徒。

而这个时候，不说话，实际上是一个更难对付的问题，之前的两军问题已经揭示了这个问题的核心——因为在异步网络中，诚实节点的消息也可能会被延迟任意久，于是在收到消息之前，你永远无法判别对方是诚实的还是叛徒。换句话说，小明在受到小红的答复之前，他永远也不可能知道小红是喜欢她，但是发出来的消息没收到，还是小红压根就不想理他。

在这种情况下，三将军问题还没开始就结束了：

1.如果指挥官是叛徒，他可能永远都不会发指令。

2.于是，为了满足终止条件，所有的士兵必须要预设一个决定，例如“没有在t之前受到命令就撤退”。 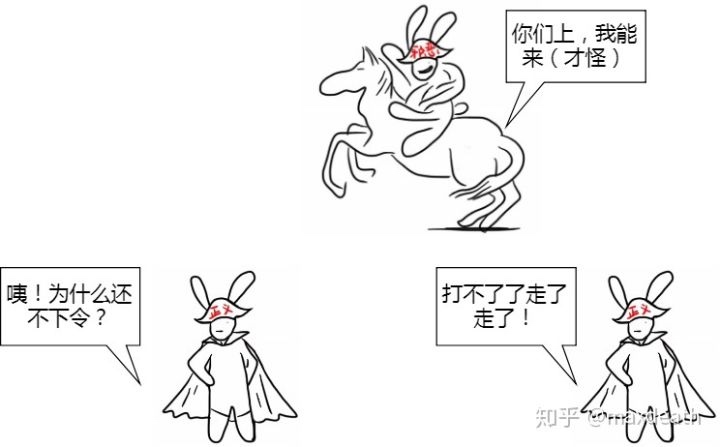为了防止指挥官有恶意，两名将军需要约定某个时间t如果指挥官不下令，就撤退

3.但如果将军是诚实的，然后消息恰好延误了超过t的时间，那么这个算法失效。 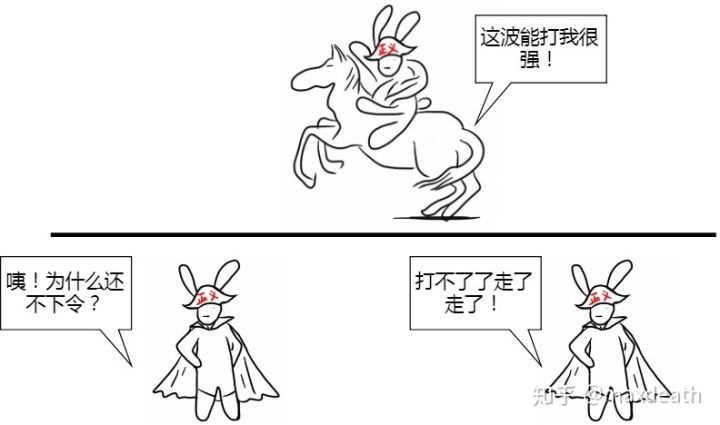但是如果恰好诚实指挥官的命令延迟了超过t的时间，就会导致不一致

似乎，我们发现了一个矛盾的问题：在三将军的异步拜占庭将军问题里，终止（活性）和共识似乎被对立起来了——如果需要这个算法能结束，那么就得给一个时限和默认决定来防止恶意节点不说话。但如果有这个，就有可能达不成共识。

实际上，这种感觉是正确的——人们很快就得出了分布式系统著名的FLP不可能理论——异步系统中，不要说拜占庭错误了，只要有一个失效错误，换句话说，只要某一个节点有可能不说话，都不存在一种确定性的算法可以保证达成共识。

这个定理的证明，实际上和我们的直觉是一致的——

首先，我们不认为一个“不管什么情况我们都无脑进攻”或者“不管什么情况我们都无脑撤退”是个合理的算法，因为这样的系统显然在实际中我们没法用。

于是，我们希望至少有的时候系统的共识是0，有的时候系统的共识是1。这其实就是更一般化的拜占庭将军问题——我们不在乎大家是不是听将军的，将军如果说了进攻最后大家包括将军都作出的决定是撤退也没事，只要大家能达成共识，而且不总是撤退就行。

然而，只要整个系统有可能有两种不同的共识的可能，就一定会出现和三将军问题一样的情况——总会有那么一种情况，所有人的决定最终会落在某位小明同学身上，这位小明同学在等着某位小红同学的消息来做判断，当她说进攻，最终整个系统的共识就是进攻，当她说撤退，整个系统的共识就是撤退。这个时候，由于是异步系统于是为了满足中止我们只能给出一个时限，例如“时间t之前如果没有收到答案，那么就默认是撤退”。而这就导致如果小红说对小明说了“进攻”可惜延迟超过t，那么算法失效。

而以上这些，仅仅是通过假装断线来实现的，换句话说，其实这个时候，拜占庭容错问题其实就变成了一般容错问题。换句话说就是，拜占庭容错这个名字听上去好像很厉害，但是最终无解的根源，仍旧是最经典的异步系统的容错问题——这个问题在分布式数据库里叫做CAP理论，简单表达起来是这样的：

“在节点可能失效的异步网络中，一致性和活性是不可能同时达成的。”

弱中止条件下的拜占庭将军问题

所以说，想要解决异步系统拜占庭将军问题，我们需要解决说假话和不说话两个问题。

而实际上，因为有了签名，如果指挥官是诚实的，指挥官以外的叛徒说假话并没有什么卵用，他们能够进行的恶意行为，只有不说话。因此，拜占庭将军问题，其实又被简化成了“指挥官说假话”和“指挥官不说话的”的问题。

而这其中，指挥官不说话的问题，刚才我们已经用例子说明了是个无解的问题——当然，如果这个问题有解，也违背了FLP和CAP。这个暂且略过不谈。

于是，我们只剩下一个问题——我们假设指挥官一定会下命令，而且每个人都知道这一点。那么指挥官说假话的时候，两个诚实的将军在异步系统里能不能达成共识？我们管这种假设叫做“弱中止假设”。

很可惜，答案还是否定的，以下是会出现的情况：

1. 指挥官会将两条不同的消息发给两个将军。
2. 两个将军必须互相交流意见，否则很显然在这种情况共识就失败了。
3. 然而，如果他们互相交流，那么又会陷入异步系统的经典问题——对方也有可能是恶意的，所以可能不会回复。所以，为了满足活性，他们必须在某个时间点，例如t，之前作出决定——如果这个决定是听指挥官的，那么如果指挥官是恶意的而两人之间的消息又恰好延迟了超过t的时间，两个诚实将军就又被恶意指挥官迷惑了；如果两人的决定是撤退，那么如果指挥官是诚实的，共识就又失败了。 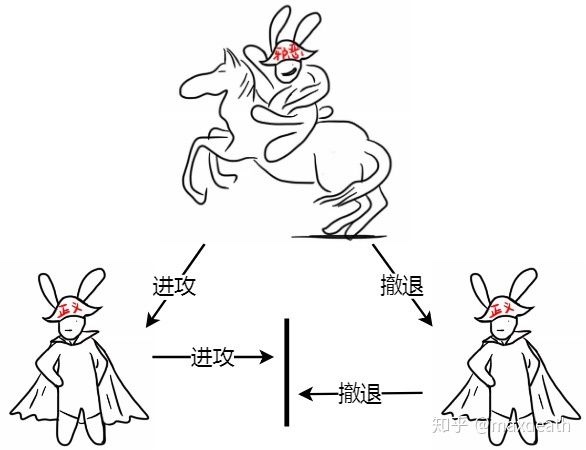诚实将军需要交流才能判断将军是不是叛徒，但是这时如果诚实将军之间的通信恰好延迟了超过阈值的时间……

也许，看到这里大家有了深深的挫败感——我们分析了这么久为什么三将军问题还是解决不了？

其实，我们已经很接近了——

这个问题，在四个将军的情况下是有解的！

算法其实很简单——每个将军等收到两个一致的命令（包括指挥官的）时就遵守，在只有一个叛徒的情况下，诚实将军是能够达成共识的。

为什么这个算法可行呢？我们从将军的角度来分析一下——

假设我是诚实将军A，我收到了命令“进攻”，因为外面最多有一个恶意节点，所以，我至少还会再收到一位将军发来的消息。

1，这个时候，我收到了将军B的消息，他说他收到的是“撤退”，并且提供了指挥官的签名。这个时候，我知道指挥官是恶意的，因为他发了两条不一样的消息。于是，我知道我们三个将军都是诚实的，那么我们一定会把自己收到的东西发出来。所以，我知道我一定会等到将军C的消息，然后，如果他说他收到的是“进攻”，我就进攻，如果他说撤退，我们就撤退。

这里，最重要的一点是——我也很清楚地知道，因为B和C也是诚实的，所以他们也会采用同样的算法，所以，我们最终会达成共识。

2，如果我收到将军B的消息，他说他收到的是“进攻”，这个时候事情就有点麻烦了——因为我这个时候还不知道谁是叛徒。

首先，假设将军B诚实，那么首先他不会撤退，因为他首先收到了“进攻”，然后，因为我发的是“进攻”，那么他最多只能收到一个撤退。接着要么将军C是叛徒，要么指挥官是叛徒。如果是前者，那么共识达成，因为指挥官和我以及将军B达成了共识，如果是后者，那么C有可能收到指挥官发的“撤退”，但他仍旧会和我们达成共识，因为我和B都发了“进攻”他最多只收到一个”撤退“。

然后我们考虑将军B是叛徒，那么他只能选择不发给C消息（他没法伪造因为他不知道将军签名），但是这不重要，考虑到我和指挥官都是诚实的，C一定能收到两条“进攻”。

所以，我能够确定无论在什么情况下大家都能达成共识，也就代表这个算法成立。而这其中最重要的部分是——当我做出决定的时候，我能肯定别人一定不会做出相悖的决定。

这个算法推而广之到n个将军的话，一般解法是这样的：

假设有n个将军，f个将军是恶意的。

那么对于任何一个将军而言，为了保证活性，他最多只能等n-f条消息（包括指挥官）就必须做出判断，否则的话就有算法就可能不会结束。

接着就是我之前加粗的那一段了——当收到多少条”进攻“的时候我才能确定别人和我的判断一致，即，他们收到的”进攻“数量无论如何都会多于”撤退“呢？假设我开始接收消息，然后接收到的一致的消息的数量开始缓慢增加，1,2,3……，直到k条。这里面有诚实节点发的，也有恶意节点发的，那么，这个k是多少的时候，我可以自信地拍胸脯打包票：

“稳了！不可能有任何一个人能收到超过k条和我不一致的消息了。”

为了求k的值，我们考虑下这种情况：假设将军B收到了k条和我不一致的消息。

如果除了指挥官之外其他人都是诚实的，那么k应该是n/2+1，因为那样就代表至少有一个节点既发了消息给我又发了消息给B，也就是说他发了两条不一致的消息，这和他诚实矛盾。 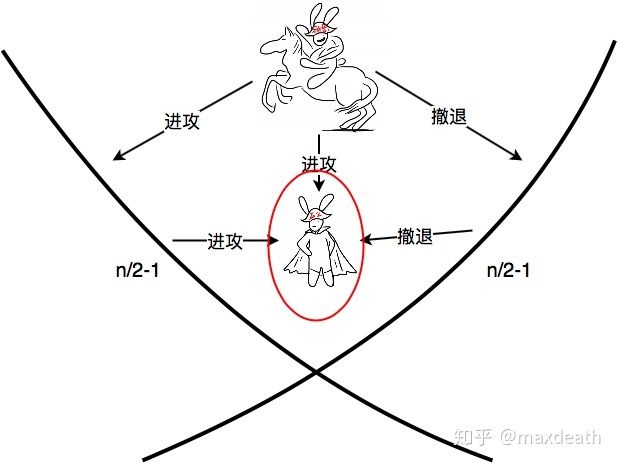当阈值k为n/2+1时，如果节点决定进攻，他会收到n/2+1（包括自己和指挥官）个进攻，他知道只剩下n/2-1的节点发了撤退，那么，即便恶意的指挥官给另一个节点发了撤退，他们最多也只能收到n/2个撤退，不会做出撤退的决定

但是现在网络里除了指挥官之外，还有f-1个恶意节点，他们如果和指挥官合谋的话，n/2+1条消息就不够了，因为其中可能有f条消息是恶意节点发的。这个时候，我们需要的消息数量是(n+f+1)/2。只有这样，我才能确定其他人能够和我做出一样的判断。 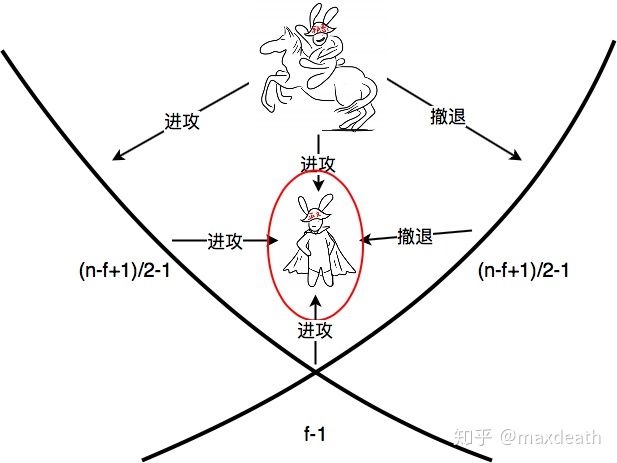这里，由于有f-1个恶意将军的存在（不包括指挥官），他们也许会给你发进攻但是给别人发撤退。所以你需要收到一共(n-f+1)/2+f-1+1=(n+f+1)/2条消息（包括自己），才能确定没有人能够收到同样多条撤退。从这图上可以清楚地看到，多出的部分，就是延伸到右边的部分。

结合这两个条件，我们知道想要这个问题有解，我们需要同时满足这两个条件，即当收到最多n-f条消息的时候，我们已经可以做出一致性的判断了，也即：(n+f+1)/2<=n-f，也就是n>=3f+1的条件下，弱中止条件下的拜占庭容错有解。

弱中止条件下的拜占庭将军问题的算法，可以说是整个异步拜占庭容错的基础，或者说，是构成之后所有拜占庭容错算法的基本要素。

大家可能注意到了，我在前面一直都只说了“拜占庭将军”，这里才开始用“拜占庭容错”这个词——因为这两者在异步系统中有一些微妙的区别……

（拜占庭将军问题可以说是拜占庭容错问题的特例——但两者的算法并不能直接相通，因为拜占庭将军问题相当于在拜占庭容错问题中，先假设能够对某个人成为指挥官这件事达成共识。多数情况下，拜占庭容错问题的解法都是基于拜占庭将军问题的解法，然后加上某些机制，这个我们下次再说）

这个算法展示了拜占庭容错的其中一个边界——如果我们牺牲活性，那么通过这个算法，我们可以达到完全的一致性。

根据这个假设我们就得到了解决拜占庭容错的一个基本思路——

我们先对网络做一定的同步性假设来保证活性，在这个前提下，采用以上的算法来达成一致。

然后，无论是传统拜占庭容错算法，还是应用于区块链的拜占庭容错算法，最终，大家都在纠结一个事：

我们要怎么做这个同步性假设。

这个问题我们留到下半部分。

————————————————————————————————

说句题外话，这个专栏在沉寂了一年之后准备开始复更。其实之前一直没写的原因是定位问题——原本的计划是技术兼具科普，所以需要加入一些有趣的东西，但是渐渐发现这个行业更急需的是干货，而不是科普，所以，我和硅谷密探合作了课程，目前第二期招生中，欢迎报名。

硅谷Live：全球仅限30人！这份给区块链爱好者的福利终于上线！

同时，我借由这个机会陆续整理了我懂的一些东西，然后系统化地讲出来。当然，一方面我也在之前的文章里承诺了——这门课程的内容，我会以科普的形式写到专栏里。而另一方面，课程的学员也强烈要求想要讲义。于是，我大概重新找到了这个专栏的定位——

这会是一个独立的，专业的关于区块链技术的专栏，主要目的，是提供一个目前整个行业里都中没有的，关于区块链技术的，中文的专业视角。

换句话说，这个专栏里只有我个人的原创，同时，只有干货，而且大概率是你在别的地方看不到的干货。所以，可能大家也能看出来，从这篇文章开始，整个专栏的内容，对于没有理工科背景或者计算机基础，以及只是想看点轻松的东西但是并不打算接受一些新知识的读者而言，可能就没有那么友好了。所以说，如果想听轻松一些的东西，欢迎收听周四（10月18日）的live。

最后，感谢 @Shirley鱼 作图！