区块链中的数学-SM2算法中的密钥交换协议
- blocksight
- 发布于 2020-08-26 14:55
- 阅读 10306
本节讲了SM2算法中的密钥协商过程,较迪菲赫尔曼密钥交换略有复杂,其实本质是一样的。最后证明了 为什么这样做可以得出相同的密钥?
写在前面
上一节说了sm2签名与验证,如果之前secp256k1的签名过程比较熟的话,sm2签名过程也就容易理解了。本文继续说下基于sm2的密钥交换协议。
在开始之前,建议先看一经典的基于指数运算的迪菲赫尔曼密钥协商,有此基础方便理解。
概述
密钥交换协议是两个用户A和B通过交互的信息传递,用各自的私钥和对方的公钥来商定一个只有他们自己知道的秘密密钥。这个共享的秘密密钥通常用在某个对称密码算法中。该密钥交换协议能够用于密钥管理和协商。
用户A的密钥: 私钥$d_A$, 公钥$P_A=(x_A,y_A)$
用户B的密钥: 私钥$d_B$, 公钥$P_B=(x_B,y_B)$
密钥交换过程
用户A和B要通过协商,产生长度为klen比特的共享密钥数据,用户A是首先发通信,用户B是响应方。 A,B用户实现如下运算步骤:
A用户第一回合:
- 用随机数发生器产生随机数 $r_A \in [1,n-1]$
- 计算椭圆曲线点 $R_A=r_A G=(x_1,y_1)$
- 将$R_A$发送给用户B
B用户第一回合:
-
用随机数发生器产生随机数 $r_B \in [1,n-1]$
-
计算椭圆曲线点 $R_B=r_B G=(x_2,y_2)$
-
从$R_B$中取出元素$x_2$,将$x_2$的数据类型转换为整数,计算:$\overline{x_2} = 2^w + (x_2 \& (2^w - 1))$
-
计算 $t_B = (d_B + \overline{x_2} * r_B)\ mod\ n$
-
验证$R_A$是否满足椭圆曲线的方程,若不满足,则协商失败;否则从从$R_A$中取出域元素$x_1$,将$x_1$的数据类型转换为整数,计算:$\overline{x_1} = 2^w + (x_1 \& (2^w - 1))$
-
计算椭圆曲线点 $V=h * t_B(P_A + \overline{x_1}R_A)=(x_v,y_v)$, 若V是无穷远点,则B协商失败;否则,将$x_v,y_v$的数据类型转换为比特串
-
计算 $K_B = KDF (x_v | y_v |Z_A |Z_B ,klen)$
-
(optional)将$R_A$的坐标$x_1,y_1$和$R_B$的坐标$x_2,y_2$的数据类型转换为比特串,计算:$S_B = Hash (0x02 |y_v | hash(x_v) | Z_A | Z_B |x_1 | y_1 | x_2 | y_2)$
-
将${RB}`$(选项$S_B$)发送给用户A;
A用户第二回合:
-
从$R_A$中提取出域元素$x_1$,将$x_1$的数据类型转换为整数,计算:$\overline{x_1} = 2^w + (x_1 \& (2^w - 1))$;
-
计算 $t_A = (d_A + \overline{x_1} * r_A)\ mod\ n$;
-
验证$R_B$是否满足椭圆曲线的方程,若不满足,则协商失败;否则从从$R_B$中取出域元素$x_2$,将$x_2$的数据类型转换为整数, 计算:$\overline{x_2} = 2^w + (x_2 \& (2^w - 1))$;
-
计算椭圆曲线点 $U=h * t_A(P_B + \overline{x_2}R_B)=(x_u,y_u)$,若U是无穷远点,则A协商失败;否则,将$x_u,y_u$的数据类型转换为比特串;
-
计算 $K_A = KDF (x_u | y_u |Z_A |Z_B ,klen)$;
-
(optional)计算 $S_1 = Hash (0x02 |y_u | hash(x_u) | Z_A | Z_B |x_1 | y_1 | x_2 | y_2)$ ,并检验 $S_1=S_B$ 是否成立,若不成立则从B到A的秘钥确认失败;
-
(optional)计算: $S_A = Hash (0x03 |y_u | hash(x_u) | Z_A | Z_B |x_1 | y_1 | x_2 | y_2)$,并$S_A$将发送给用户B。
B用户第二回合:
- (optional)计算: $S_2 = Hash (0x03 |y_v | hash(x_v) | Z_A | Z_B |x_1 | y_1 | x_2 | y_2)$ 并检验 $S_2=S_A$ 是否成立,若不成立则从A到B的秘钥确认失败。
到此结束,仔细看的话,会发现计算过程有个w, w的值可以预先算出来:$w=[[\log_2(n)]/2]-1$。(注:此处的[]指的是顶函数)
$Z_A,Z_B$是由用户身份ID加上一些公共参数经过摘要算法得到, 具体可参考上篇sm2签名与验证。
还有KDF密钥导出函数,以前说过,在本文最后相关阅读部分可以找到。
整体流程图如下:
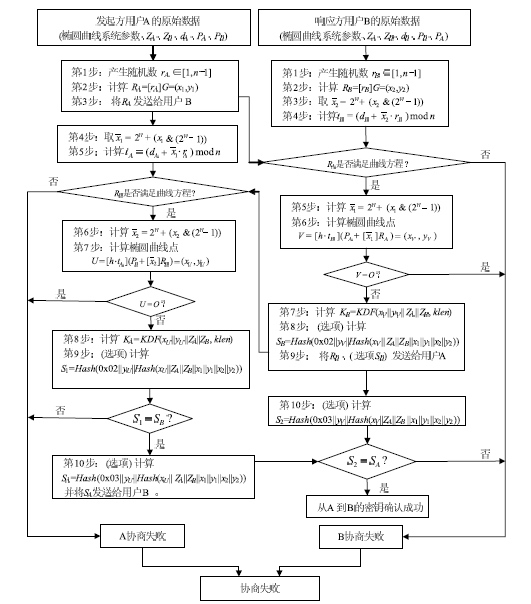
为什么能得到共同的密钥?
思考这个问题之前,需要先回答如果得到了共同的密钥,那么将是什么? 不难猜到,得到的共同密钥是$K_A$和$K_B$
只要二者相同,也就达到了密码协商的目的:用户A,B独自计算出一个相同的秘密值。
那$K_A$和$K_B$相不相同呢?这里仔细分析下。
$K_B = KDF (x_v | y_v |Z_A |Z_B ,klen)$ $K_A = KDF (x_u | y_u |Z_A |Z_B ,klen)$
观察这两个式子,只要 $x_v | y_v$ 与 $x_u | y_u$ 相同就可以,而这两者分别是U,V的坐标,问题转化成了 U = V 。
下面看下U和V是否相等?
$V=h * t_B(P_A + \overline{x_1}R_A)$ $U=h v t_A(P_B + \overline{x_2}R_B)$
相同h可以消去,消去h后用 表示:
$V_h = t_B(P_A + \overline{x_1}R_A)$ $U_h = t_A(P_B + \overline{x_2}R_B)$
$t_B$表达式代入
$V_h = (d_B + \overline{x_2} r_B)(P_A + \overline{x_1}R_A)$ $=d_BP_A + d_B \overline{x_1}R_A + \overline{x_2}r_B P_A + \overline{x_2}r_B\overline{x_1}R_A$ $=d_BGd_A + d_B \overline{x_1}r_AG + \overline{x_2}r_BGd_A + \overline{x_2}r_B\overline{x_1}r_AG$ $=d_AP_B + \overline{x_1}r_AP_B + \overline{x_2}R_Bd_A + \overline{x_2}R_B\overline{x_1}r_A$ $=(d_A + \overline{x_1} r_A)(P_B + \overline{x_2}R_B)$ $=t_A(P_B + \overline{x_2}R_B )$ $=U_h$
依次回推, 可得 $K_A=K_B$
小结
本节讲了SM2算法中的密钥协商过程,较迪菲赫尔曼密钥交换略有复杂,其实本质是一样的。最后证明了 为什么这样做可以得出相同的密钥?
知其然知其所以然是我们一贯坚持的原则!
本文内容主要参照 《《GBT 32918.2-2016 信息安全技术 SM2椭圆曲线公钥密码算法 第3部分:密钥交换协议》
好了,下一篇继续说sm2的一些实现相关的内容。
欢迎关注公众号:blocksight
- Uniswap v3 数学洞察系列翻译 —— 第六部分 共 6 部分 3836 浏览
- Uniswap v3 数学洞察系列翻译 —— 第五部分 共 6 部分 3944 浏览
- Uniswap v3 数学洞察系列翻译 —— 第四部分 共 6 部分 4381 浏览
- Uniswap v3 数学洞察系列翻译 —— 第三部分 共 6 部分 5239 浏览
- Uniswap v3 数学洞察系列翻译 —— 第二部分 共 6 部分 3345 浏览
- Uniswap v3 数学洞察系列翻译 —— 第一部分 共 6 部分 3924 浏览
- stark数学基础和翻译名词 3250 浏览
- 区块链中的数学--PLookup 7279 浏览
- 区块链中的数学 -- MultiSet check& Schwartz–Zippel lemma 6784 浏览
- 区块链中的数学 - 环签名(ring signature) 16082 浏览
- 区块链中的数学 -盲签名(Blind Signature) 13869 浏览
- 区块链中的数学 - sigma协议OR Proof&签名 7798 浏览

