区块链中的数学-数论的一些知识和椭圆曲线上加法运算

写在前面

前面说过密码学是区块链的基石，没有密码学技术，区块链就是空中楼阁，也难以存在。密码学的基石是数学。

上一节我们介绍了椭圆曲线的方程式，本节主要说涉及到数论的一些知识和椭圆曲线上加法运算。

群与阿贝尔群

首先说下群论的基础。代数中的群简单来说就是一组元素集合和定义在元素上的运算。比如说全体整数构成了一个群，运算包括加法等。这里的集合用 G（group）表示，集合要变成群，一般要满足以下性质：

1.封闭性：如果 a和b都属于G集合，那么a+b 也属于G;

2.结合律：(a+b)+c=a+(b+c)

3.存在单位元（在二元运算中，单位元指与任意元素运算不改变其值的元素，以实数为例，乘法单位元为1，加法单位元为0）O使得

a+O=O+a=a ;

4.每个元素都存在逆元素，就是说对于任意元素a必存在b使得a+b=O(O是单位元) 。

集合满足以上四个性质就是称为群，还有一些特殊的群，如阿贝尔群（Abelian Group）除了满足群的基本性质，还满足交换律即：

a+b=b+a

故阿贝尔群又称交换群。根据这些性质，我们可以知道整数集Z是一个阿贝尔群，自然数集N却并不是一个群，因为它不满足第四条性质。

好了，群论基础知识先到这里（看似比较简单，也有很多复杂特性暂时省略）。需要注意的是，群中的集合元素，可以是数，也可以是其他类型元素，比如解析集合中点（坐标形式）等。

椭圆曲线上的群

有了群的基本知识，我们就可以进一步类似的定义椭圆曲线上的群了。刚才我们说群的元素可以是任意类型，椭圆曲线上的群元素是椭圆曲线上的点 单位元是无穷远点记为O（关于无穷远点请参考上一篇射影平面与椭圆曲线）。任意点P的逆是该点关于x 轴对称点。

椭圆曲线群的加法也不同于整数的加法，它的加法定义可以描述为：

给定三个共线非零的点 P ，Q，R ，它们的和为 P+Q+R=O。

几何意义是：

过𝑃、𝑄两点做直线𝐿，与椭圆曲线相交于第三点，该点关于X轴的对称点即是所求的𝑅点。椭圆曲线的这种加法运算有比较明确的几何含义。如下所示：

下面处理一些异常情况：

1 𝑂+𝑂=𝑂，对任意的𝑃，有𝑃+𝑂=𝑃；𝑂看做零点

2 𝑃=(𝑥,𝑦) 的负元是关于X中对称的点−𝑃=(𝑥,−𝑦)（而不是关于原点对称），𝑃+(−𝑃)=𝑂，可以看做P与-P连线与椭圆曲线相交于无穷远点

3 计算𝑃点（𝑃≠𝑂）的两倍时，是做该点的切线，再取切线与椭圆曲线交点𝑆关于X轴的对称点−𝑆，也即是2𝑃=𝑃+𝑃=−𝑆，得出2倍值可以递推到若干倍。

可以看出，椭圆曲线的点集（包含无穷远点O）和上述定义的加法运算构成了一个阿贝尔群： 单位元是𝑂点，𝑃(𝑥,𝑦)的逆元是𝑃(𝑥,−𝑦)，封闭性，结合性以及交换性也是显然满足的。

椭圆曲线群代数运算

几何解释方便理解椭圆曲线点加法的意义，代数解释更易于运算。过曲线上$𝑃(x_p,y_p)$和$Q(x_q,y_q)$两点（𝑃和𝑄不互为负元）做直线，求与曲线的第三个交点的问题是很容易用代数的方法来描述的。

也即是求：

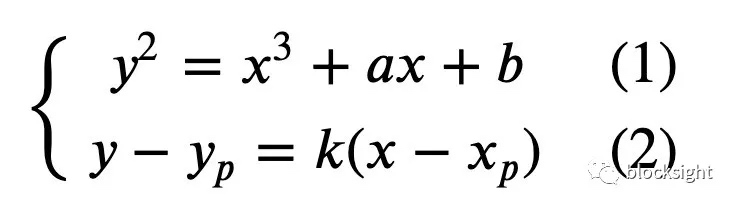
其中斜率$𝑘=\frac{y_q-y_p}{x_q-x_p}$

将（2）代入（1）再利用次数对齐的方式容易求得第三个交点的对称点，也即𝑃,𝑄之和$𝑅(x_r,y_r)$为：

$x_r=k^2-x_p-x_q$ $y_r=-y_p+k(x_p-x_r)$

如果P=Q，则两者相加就是计算倍乘，可以让多个点自身重复相加得到。例如𝑃+𝑃=2𝑃=𝑅，当≠0时，代数描述为：

$x_r=((3x_p^2+a)/2y_p)^2-2x_p$ $y_r=((3x_p^2+a)/2y_p)(x_p-x_r)-y_p$

到这里，椭圆曲线群元素在实数域上的运算基本明了，但对于椭圆曲线上实现加解密运算足够了吗？答案是还不够，但是已经很接近了。下一篇将介绍密码学中椭圆曲线算法实际用到的群域和运算。

欢迎关注公众号：blocksight